基于OWA算子-偏序集的城市新能源发展评价
薄靖凯 温廷新
(辽宁工程技术大学 工商管理学院,辽宁 葫芦岛123000)
0 引言
中国是世界上人口最多的发展中国家。国家经济的发展离不开丰富的蕴藏能源的支撑。随着经济的高速发展,环境污染问题也随之出现[1]。发展城市新能源已成为必然趋势。 全面发展需坚持以人为本,树立全面协调可持续发展观,促进经济社会和人的全面发展。着眼于自然、经济,对社会复杂系统进行全面思考。目前我国能源利用率与科学发展观的战略要求还存在较大差距。在该背景下,发展新能源应运而生。所谓新能源,是指在利用高新技术的基础上开发与利用的可再生性能源,例如太阳能、风能等。随着技术的发展,发展新能源电力成为当前能源供给领域的研究重点。电力工业节能在我国资源节约工作中占有重要地位。虽然发展新能源电力已成为世界各国的广泛共识,但不同国家在新能源资源、技术水平和社会环境等方面存在的差异化使得各国新能源电力发展重点不同。
发展新能源已得到各国广泛认同,不同地区的新能源资源禀赋不同,受技术实现、多属性需求的影响,其新能源发展重点各不相同。Edwards[2]以属性权重赋权为基础,提出了确定属性排序即可确定属性权重的SMARTER方法。针对简单系统结构建模无法处理相关性强、因素较多的决策问题,Loken[3]利用层次分析法(AHP)、加权平均方法(WA)等解决新能源优先发展排序问题。该方法适用于假设水泥构件偏好独立且难以进行客观决策的情形。还有学者[4]提出采用模糊方法和灰色关联对新能源优先发展顺序进行排列。现有文献虽然对多指标排序问题进行了深入研究,但是目前仍然存在两方面问题:一是在指标权重的设置;二是现有文献过于强调指标间的独立性。这种常权评价导致指标间的互补性太强。针对常权的不足,可以采用变权方法。Sugeno、Chopuet积分[5]以及关联有序加权平均算子等被提出用于指标权重计算。李德清[6]研究了状态变权向量的变权效果,发现能源-经济-环境-社会系统指标偏好交互影响,互补性太强,治标不能完全独立;Sugeno[7]提出模糊测度概念,采用Choquet积分、关联有序加权平均算子(R-OWA)讨论了基于模糊测度的状态变权公式;岳立柱[8]研究了蕴含权重的偏序集多准则决策。本文在区间数和R-OWA算子的基础上通过构建指标偏好间存在交互作用的区间有序加权算子在此基础上指标偏好存在交互作用的变权区间有序加权平均方法应用偏序集进行偏好下排序。
1 模型构建
针对新能源发电效绩评价问题,假设需要评价的新能源种类集合为O={O1,O2......,On},需要考虑的评价指标集为C={C1,C2......,Cm}。
1.1 偏序集基础概念[9]
定义1:设R是集合A上的一个二元关系,若R满足
(1)自反性。 对任意x∈A, 有x≤x;
(2)反对称性。 对任意x,y∈A,若x≤y且y≤x,则x=y;
(3)传递性。 对任意x,y,z∈A,若x≤y且y≤z,则x≤z。则称为A上的偏序关系[1]。

偏序集表示原理。由比较关系矩阵R可以导出Hasse图,对偏序关系进行清晰地呈现。比较关系矩阵与Hasse矩阵相互转化的关系为:
HR=(R-I)-(R-I)2
(1)
其中,R为关系矩阵,HR为Hasse矩阵,I为单位矩阵,矩阵(R-I)2为布尔运算(该式不出现取值相同的方案)。
1.2 OWA算子概念
(1)指标权重计算。区间数相离度定义及最大偏差原理可用于确定区间值指标权重。当不考虑指标偏好间的交互作用时,指标权重反映了各指标在整个评价过程中的贡献度,这与考虑了指标间交互作用的指标值Shapley的定义吻合。因此,可利用区间值相离度计算指标值Shapley,如下所示。
(2)

为度量模糊测度不确定性,文献[3]定义了模糊测度的Marichal熵。与Shannon熵类似,Marichal熵具有有界性、单调性等特征。根据指标值Shapley和模型(2),利用Matlab求解,可得到各指标(集)权重(λ模糊测度)。
(2)OWA算子构建[10]。考虑到各评价指标的区间取值,集成区间值、λ模糊测度和R-OWA算子,构建OWA算子并对OWA算子性质进行讨论。
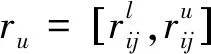
1.3 状态变权向量的设置
考虑不同地区的条件与需求不同,如经济基础、技术水平存在差异,新能源产业的选择也不同,对不同指标的赋值也会有所不同。所以,需要基于变权多指标对新能源发展体系进行评价,偏序集决策处理后的状态变权函数是实施变权评价的核心。结合不同地区,构建不同的状态变权公式。
(1)惩罚性变权函数的构建[4]。经济发达地区或者旅游型城市可能更关注其弱项指标;在经济技术条件优越或必须保证环境的前提下,决策者往往更看重环境和社会指标,目的是在追求经济发展的同时,保证环境的可持续性和社会的平衡性(旅游支柱不被影响)。此时,可采用惩罚性变权函数(式3)对指标贡献程度进行修订。
(3)
其中,i=1,...,n;j=1,...,m。
式(3)满足上述定义中的公理(T1)、(T2),即∀oi(∈O)的惩罚型R-变权向量为:
(4)
(2)激励型变权函数的构建。经济欠发达或者拥有天然地理优势的地区可能更注重其强项指标。例如在发展中国家或者地区,由于其技术落后、经济欠发达,决策者可能更看重强项指标(例如环境等指标)。在这种情况下,适和采用激励型函数来调整状态。
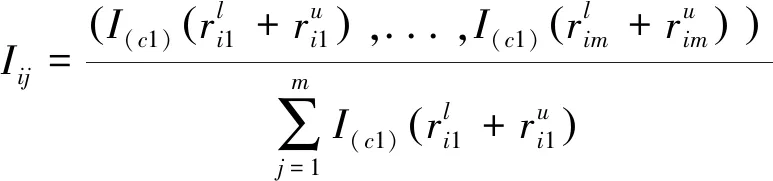
(5)
推论:将惩罚型状态下的变权值Shapley利用模型计算权重,再代入公式(5),得到惩罚型状态偏序集决策模型,将比较关系矩阵变成Hasse矩阵,得到加入惩罚因子后的Hasse图。激励型状态矩阵按上述相同步骤进行处理后,得到激励型状态偏序集决策模型。由Hasse矩阵可以绘制出Hasse图[20],可以直观地观察激励型或者惩罚型下的Hasse图,反映了方案排序。当由于特殊原因导致权重变化时,排序结果也随之改变。
1.4 OWA算子偏序集求解办法步骤
可将基于OWA算子偏序集办法的新能源发展效绩评价步骤归纳如下:
步骤一:确定新能源种类对象C和指标体系M;
步骤二:构建评价方案体系并确定各指标值范围,由此建立评价矩阵R=(Cij)n×m;
步骤三:根据指标类型,对各指标进行数据清洗和规范化处理,得到规范化评价矩阵R;
步骤四:利用公式求解Shapley值,加入偏好指标R-变权向量和变权Shapley值进行计算;
步骤五:根据指标权重进行排序,由变权向量得到Hasse矩阵,绘制Hasse图,再进行基于OWA方法的典型城市新能源发展效绩评价。
2 OWA方法——将偏序集决策方法应用于典型城市的发电效绩评价
2.1 评价方案及评价指标体系构建
新能源发展体系是一项涉及范围广、影响因素较多的复杂系统,因此需要建立设计合理、易操作的城市新能源评价指标体系和发展原则,并结合实际情况建立科学有效的统计制度以为其提供保障和依据,同时,指导企业制定城市新能源发展规划。
经过科学合理的数据整合和实际情况调查,影响城市新能源发展的因素主要涉及经济发展、环境保护、社会稳定等方面,需要从多角度、多层次考虑,同时兼顾时间等因素,以便根据不同资源禀赋和发展基础来调整新能源发展策略。通过调查,主要选用了劳动就业情况、GDP贡献度、项目盈利能力、土地征用、社会认同度、温室气体排放、环境污染、单位投资比等9个影响因子以及十类城市发展新能源,如生物柴油、燃料乙醇、沼气工程、生物质燃料发电、成型燃料、垃圾发电、热泵技术、太阳能热利用、光伏发电、风力发电[11]。
2.2 偏好排序
泰安市是一个自然景观旅游城市,近年来其努力打造生态旅游和发展新能源产业,在新能源产业装备方面建立起有力的支撑体系。目前,其以太阳能热利用(太阳能热水器,多晶硅太阳能电池组件)、风力发电技术(输变电器材)、生物质直燃发电为主导,产业链不断完整,新能源产业体系已初具规模。本文利用泰安市年鉴获得相关数据,就惩罚型状态变权下的偏序集决策评价结果进行分析。
首先,加入惩罚型函数,给指标权重排序。根据以上影响因素和新能源种类,每一种新能源对城市的影响都是多方面、复杂的,通过指标量化并计算出现有基础上的新能源比较矩阵。其次,采用偏序集,对惩罚型因子下的泰安市新能源进行排序。将各指标在新能源下的规范值数据汇总,得到不考虑指标偏好间交互作的比较矩阵,如表1所示。

表1 指标比较矩阵
不考虑偏好下的效绩检验。为综合数据平均值,不考虑不同主体对评价指标关注度的差异,基于比较矩阵,采用偏序集Hasse图来表示各新能源比较关系,如图2所示。利用Matlab,计算指标因子影响权重,排序为单位投资比>社会认同度>劳动就业>GDP贡献>温室气体排放>环境污染(温室气体)>土地征用,新能源无偏好偏序集排序偏序集的Hasse图如图2所示。

图1 无偏好偏序集排序偏序集的Hasse图
偏序集的比较矩阵结果见表2所示。无偏好下的新能源发展排序为生物柴油>燃料柴油>沼气工程>生物质直燃发电>成型燃料>垃圾发电>热泵技术>太阳能热利用>光伏发电>风力发电。该新能源发展排序对国家或大型地区的整体发展具有参考价值。针对不同城市或地区的不同主体问题,关注度不同会导致权重偏好交互问题,不利于评价。本文根据参考变权公式,加入惩罚型因子以评价泰安市新能源发展排序。

表2 指标偏好间交互作的比较矩阵
加入惩罚因子变权下的发展排序及相关分析。基于变权思想,加入惩罚型函数,计算指标值shapley,再结合公式计算指标变权向量,计算惩罚型变λ模糊测度(权值),结果见表3。根据指标权重和λ值对影响因子进行排序,整理惩罚型因子影响下的比较矩阵,如表4所示。

表3 惩罚型变λ模糊测度(权值)
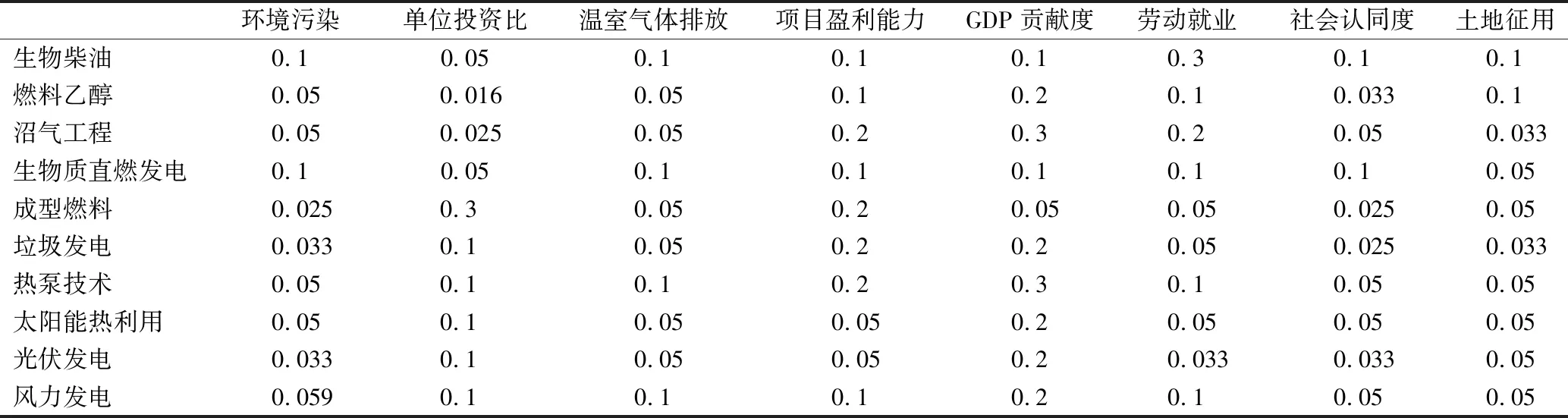
表4 加入惩罚因子的比较矩阵
图2加入惩罚因子的比较矩阵。偏序集排序下的Hasse矩阵新能源排序关系如图4所示。偏序集比较矩阵结果如表5所示。
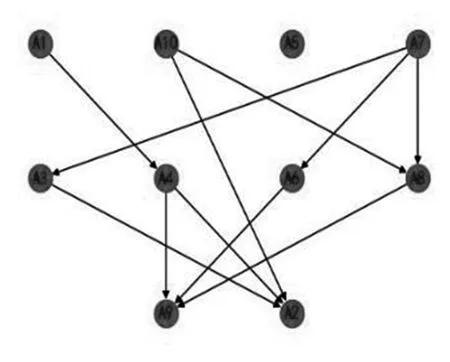
图2 偏好排序下的Hasse图
由于新能源评价指标体系中普遍存在指标偏好间具有交互作用,指标权重具有不确定性,因此本文在模糊测度和R-OWA算子等理论基础上构建了指标交互作用的变权方法,计算偏好下的各指标权重,再通过偏序决策进行排序,依据城市或地区可能存在的偏好,采用惩罚型和激励型两类变权函数公式,将偏序集决策进行排序。通过实例验证发现,指标权重值的设置对新能源评价结果具有很大影响。无偏好的优先发展排序为生物柴油、燃料乙醇、沼气工程、生物质直燃发电、成型燃料、垃圾发电、热泵技术、太阳能热利用、光伏发电、风力发电;惩罚型状态变权下的泰安市新能源评价指标优先发展排序为太阳能热利用、垃圾发电、土壤、水源热泵、风力发电、光伏发电、沼气工程、直燃发电、燃料乙醇、生物柴油。

表5 偏好因子下的新能源排序
3 结语
本文给出了OWA算子与偏序集决策矩阵算例并得出以下结论:
(1)采用模糊测度作为指标权重,适用于指标间存在偏好交互类型的多指标评价问题。
(2)由于各城市(地区)存在指标偏好因素,该模型为解决这类问题提供了新思路和改进路径。
(3)此模型融合了OWA与偏序集决策,有一定创新性。本文采用两种偏好影响模型,可以根据不同需求,为具有更多偏好的变权函数建立评价体系。

