基于多相质点网格法的大气污染仿真模拟

于潇萌， 曹 乐*， 严家德， 王巍巍

(1.南京信息工程大学中国气象局气溶胶与云降水重点开放实验室，南京 210044；2.南京信息工程大学中国 气象局综合气象观测实习基地，南京 210044；3.南京信息工程大学大气与环境实验教学中心，南京 210044)

近年来，随着城市化与工业化进程的不断推进，大气污染问题日益严重。为了更好地完成空气污染问题的综合治理，学者们在大气环境领域做了诸多研究[1]，以预测空气污染物的散布及变化规律。这些研究包括对下垫面条件的处理、大气扩散与大气输送的尺度的拓展、多层次污染之间的相互作用等多个方面，其研究成果也被广泛应用于城市规划、生态建设、信息通信、医疗健康等不同领域。而当前大气环境污染相关研究工作的瓶颈之一，在于如何准确模拟大气污染物的扩散规律[2]。大气污染物扩散规律制约众多，包括了多变的气象条件、污染源排放特性、下垫面边界条件、复杂物理化学过程等因素，因此学者们开发出了众多有着不同适用范围的扩散模型，以应对复杂的影响因素。而选取适当的扩散模型有助于更好地提高扩散模拟的质量，改进区域环境质量的预报效果[3-6]。

目前应用相对广泛的大气扩散模型大致可分为两类[7]，一类是基于高斯理论的半经验模型，另一类是计算流体动力学(computational fluid dynamics，CFD)模型。相比较简单的高斯经典扩散模式，CFD模型可以更好地刻画湍流以及复杂地形条件对污染物扩散造成的影响[8]，因此，CFD模拟成为了大气污染模拟的主要手段[9]，并被广泛应用于不同尺度的大气流动和扩散问题上[10]。Rahimi等[11]用CFD模型模拟了伊朗伊斯法罕炼油厂不同烟囱释放的气体污染物的扩散，比较并考虑了3种不同湍流模型(k-ε模型、RNGk-ε模型、realizablek-ε模型)对扩散造成的影响，并将模拟结果与炼油厂实际观测数据进行对比验证。Jeanjean等[12]利用OpenFOAM软件平台，采用k-ε模型对大气污染物浓度进行了CFD模拟，以研究树木与气流动力学之间的相互作用。Tominaga等[13]通过比较不同羽流浮力条件下的RANS模拟结果，与实验结果对比验证，探究使用Boussinesq近似进行RANS(reynolds-averaged navier-stokes)模拟的可行性。杨光俊等[14]为研究燃煤电厂的烟气扩散，采用CFD方法，对燃煤电厂两种排放方式(烟塔合一和烟囱结构)的扩散形态进行模拟。

然而，当前诸多应用CFD软件的数值模拟研究，多数聚焦于不同排放源诸如火电厂、冷却塔、汽车尾气等对污染扩散造成的影响，或关注于空气污染物输送过程中化学转化、干沉降和湿沉降清除等对污染扩散的作用，对于湍流作用下污染物扩散具体形态变化及浓度变化定量分析的研究还比较少。而离散粒子法(discrete particle model，DPM)[15]经过学者们的验证，可以准确模拟湍流作用下颗粒污染物的扩散形态变化与浓度变化情况。荣双等[16]应用DPM方法研究街道峡谷内不同高度处污染物浓度的影响，结果表明风向与街谷长宽比的变化都会对污染物的浓度产生影响。付志民等[17]为研究街道峡谷的不同几何结构对风场与污染物的影响，采用DPM方法进行模拟，结果表明递增型街谷模型更有利于颗粒污染物的扩散。

但是，传统DPM方法在计算粒子之间碰撞作用的计算量极大，难以应用到范围较大的污染物扩散模拟中，因此只适用于室内或短距离之间的污染物扩散模拟。而以DPM为基础发展起来的多相质点网格方法(multi-phase particle-in-cell，MP-PIC)[18]以固相应力的方式取代颗粒之间的碰撞过程，可以大大提高计算效率，也为提高拉格朗日粒子模型的预报尺度提供了可能。因此，使用以MP-PIC为基础的拉格朗日粒子追踪模型，对理想条件下大气污染扩散问题进行大涡仿真模拟，从而分析污染物扩散形态变化特征及污染物数浓度时空分布变化特征，以探究不同风速条件下湍流对污染物扩散造成的影响。这一工作无论在大气环境模式发展，还是空气质量预报业务，亦或者关于大气污染潜在影响的研究中都具有相当的应用价值。

1 研究方法与算例设置

本文所使用的计算平台为开源软件OpenFOAM(open field operation and manipulation)[19]，并利用基于MP-PIC方法的拉格朗日粒子模型对单点源污染物不同风速条件下的扩散情况进行模拟计算。下面对软件平台及具体求解器进行详细介绍。

1.1 求解器介绍

OpenFOAM作为一款基于Linux 平台的开源软件，其本质是一个功能强大的预编译功能库。它自带许多开发完备的基础算例与现成的求解器，用户可以通过命令直接调用求解器对具体问题进行求解，或根据需要对这些功能库进行修改以满足自己的需求[20-21]。这些标准求解器包括了不可压缩流求解器、可压缩流求解器、多相流求解器等。而本研究选用标准求解器MPPICFoam作为求解器，该求解器为瞬态流体-固体粒子求解器，可以将粒子打包为粒子云，同时附带离散相对连续相的影响，适合研究气固两相流之间的相互作用。

MPPICFoam中所使用的MP-PIC方法于1996年被提出，最初被应用于模拟密相颗粒流的工作。该方法将流体视为连续相、颗粒视为离散相进行求解，分别采用欧拉坐标系与拉格朗日坐标系进行描述，以追踪粒子的具体轨迹[22-23]。与传统DPM方法相比，MP-PIC方法用固相应力的方式取代颗粒之间的碰撞过程，可以大大提高计算效率。

在MP-PIC方法中，气相连续性方程为

(1)

式(1)中：θg表示气相体积分数；ρg表示气相密度，kg/m3；ug表示气相速度，m/s。

而气相动量方程可表示为

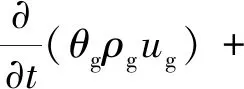
·θgτg+θgρgg-F

(2)

式(2)中：τg表示气相应力张量，Pa；p表示压强，Pa；F表示气固相间动量交换力，N/m3，即颗粒所受到的拖曳力；g表示重力加速度，m/s2。τg的表达式为

(3)

式(3)中：μ1为分子黏度，kg/(m·s)；μt为湍流黏度，kg/(m·s)，可以由次网格模型计算得出；S表示形变率张量，s-1；I为单位张量；S可表示为

(4)

相比于气相方程，固相粒子在空间中的分布情况可表示为[24]

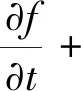
(5)

式(5)中：f表示粒子分布函数；up表示了平均粒子速度，m/s；A表示粒子加速度，m/s2，其表达式为

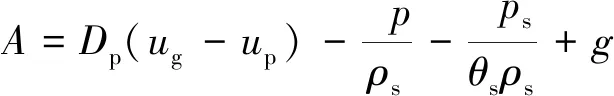
(6)

式(6)中：Dp表示阻力系数，s-1，θs、ρs分别表示固相体积分数、固相平均密度，kg/m3；ps表示固相应力，Pa。其中，固相体积分数θs与气相体积分数θg之间满足关系式：

θg+θs=1

(7)

而固相应力ps的表达式为

(8)

气相与固相之间通过气固相间动量交换力F(单位为N/m3)进行耦合，F与粒子分布函数f之间的关系为

F=∭fVp[βp(ug-up)-p]dVpdρsdup

(9)

式(9)中：Vp为气相体积，m3；βp表示曳力系数，kg/(m3·s)，具体公式可参考文献[24]。

本次模拟中湍流模型采用大涡模拟(large eddy simulation，LES)，应用的次网格模型为Smagorinsky模型[25]，次网格尺度涡黏计算公式为

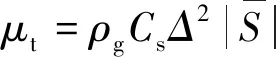
(10)

式(10)中：Cs表示模型常数；Δ为过滤尺寸长度，

表示过滤后的应变率，s-1，表达式为

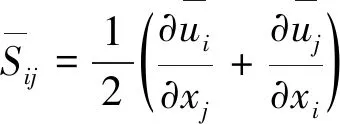
(11)

1.2 算例基本设置

图1所示为本次模拟的计算区域设置，整个计算区域形状为长方体，大小为1 500 m×200 m×200 m。左侧为计算域入口，而污染源距离左侧入口约100 m，污染源高度为10 m，对外不断垂直向上射出粒子，喷射口面积为10 m×10 m。假设风向沿x轴正方向，且y方向速度梯度为0，100 m以上风速为参考风速，100 m以下风速随高度z的变化满足大气边界层风廓线形式，即

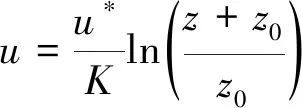
(12)

式(12)中：u表示z高度处的风速，m/s；u*表示摩擦速度，m/s，u*的取值可以根据100 m高度处参考风速求出；K为冯卡门常数，取值为0.41；z0=0.1，代表粗糙度长度，m。

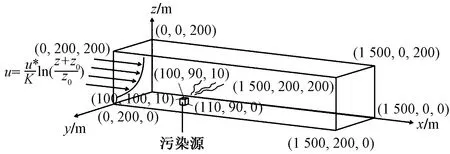
图1 计算区域设置Fig.1 Computational domain configurations

本次模拟共设置a、b、c三组算例进行对比，其入口参考风速分别为2、5和10 m/s，以讨论不同平均风速对扩散的影响。模式模拟的基本参数设置如表1所示。整个计算域网格数共计500×40×100=200 000个，模拟时长为1 200 s，喷射口粒子的喷射速度为垂直向上2 m/s，每秒喷射粒子1 000个，粒径大小为0～200 μm，平均粒径为100 μm，且假设其满足标准正态分布。地面反射系数设为0.8，入口施加随机脉动(±0.02, ±0.02,±0.01)m/s。计算中所选取的大涡模型为Smagorinsky模型。为保证数值稳定及时间计算精度，最大库朗数设为0.6，最大时间步为1 s，并且每10 s输出一次计算结果。

2 计算结果与分析

选取流场稳定状态1 200 s时的数据进行分析，输出11 m高度风速图以体现流线变化情况。选取11 m高度处流线的原因是该处流场可充分体现源项上方的气流变化情况。图2所示为11 m高度处

表1 模式基本输入参数

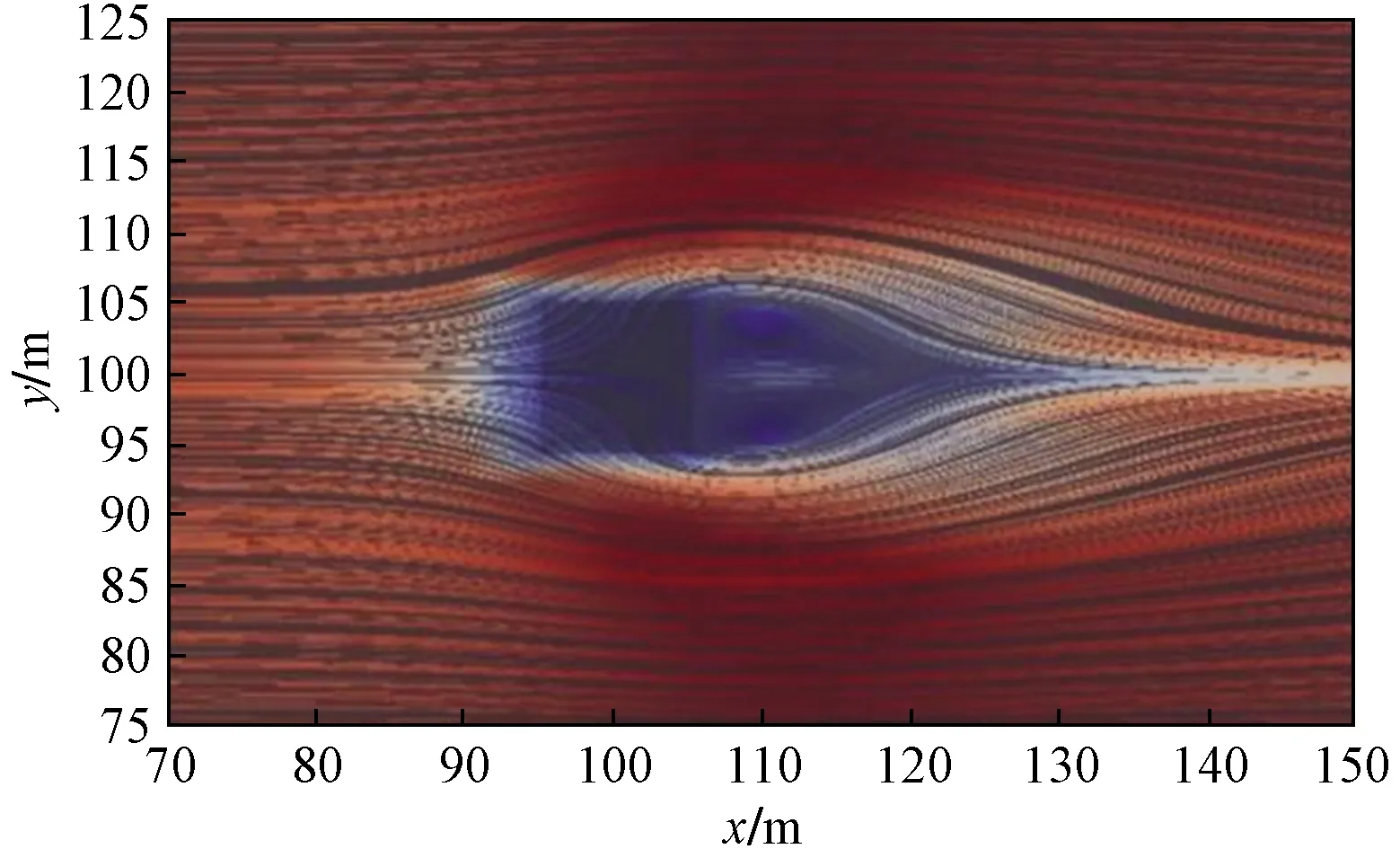
图2 流场稳定时(t=1 200 s)流线分布Fig.2 The distribution of the stream line when the flow field becomes steady (t=1 200 s)

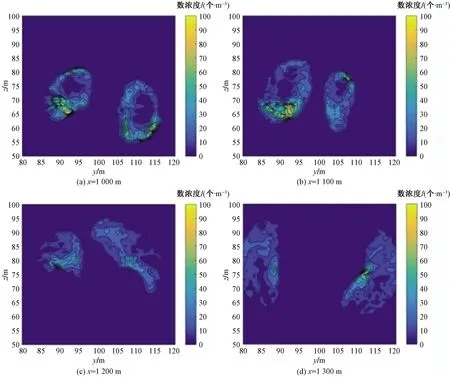
图3 算例a中t=1 200 s时下风向不同距离截面处污染物的数浓度空间分布Fig.3 The spatial distribution of pollutant number concentration at t=1 200 s in case a

流线分布示意图，图中可以明显看到：由于污染源对入口风速存在阻挡作用，源项周围出现明显绕流作用，源项后方出现旋转方向相反的对称涡旋。该绕流现象会导致污染物扩散时的分裂现象，具体变化情况在后文中详细描述。

图3所示为算例a(入口风速为2 m/s)t=1 200 s时刻计算域下风向1 000、1 100、1 200、1 300 m处污染物的数浓度空间分布。由于y方向速度梯度为零，且入口风速较小，污染物始终分裂成两股，未发生汇合，两股污染物之间距离为5～20 m。距离入口1 000 m处污染物数浓度最大值为78个/m3，1 100 m处数浓度最大值为70个/m3，1 200 m处数浓度最大值为80个/m3，1 300 m处污染物数浓度最大值为87个/m3。

图4所示为算例b(风速大小为5 m/s)t=1 200 s时刻计算域下风向不同距离处污染物浓度空间分布。图中可见：随着风速的增大，分裂的两股污染物之间的距离减小，主体污染物距离约在2～10 m左右。下风向1 000 m处污染物数浓度最大值为300个/m3，1 100 m处污染物数浓度最大值为212个/m3，1 200 m处数浓度最大值为227个/m3，1 300 m处污染物数浓度最大值为257个/m3。

图5所示为算例c(风速大小为10 m/s)计算时间达到1 200 s时计算域内下风向不同距离污染物数浓度空间分布。从图5中可以看到：风速的增大使得喷射口对于入口风的阻挡作用减小，该算例中污染物在扩散过程中未发生分裂；算例c中下风向1 000 m处污染物数浓度最大值为413个/m3, 1 100 m处污染物数浓度最大值为502个/m3, 1 200 m处污染物数浓度最大值为407个/m3, 1 300 m处污染物数浓度最大值为409个/m3。这些算例中污染物浓度随风速增大而增大的原因在于入口风速的增大使得污染物粒子在计算域内停留时间变短，从而导致粒子位移距离减小，浓度增大。

图5 算例c中t=1 200 s时下风向不同距离截面处污染物的数浓度空间分布Fig.5 The spatial distribution of pollutant number concentration at t=1 200 s in case c

图6 污染物中心高度-时间变化曲线Fig.6 The temporal change of the height of the pollutant center

图6显示了下风向1 500 m处污染物数浓度最大值的高度随时间的变化趋势。图中可见，随着湍流的扰动作用，算例a污染物中心(浓度最大值)高度在63～76 m，算例b污染物中心高度约在46～52 m，算例c污染物中心高度在36～41 m。因此，风速的增大使得污染物浓度最大值高度减小，且波动范围减小。图7所示为下风向1 500 m处不同风速条件下粒子最大抬升高度随时间变化曲线。随着风速的增大，粒子最大抬升高度逐渐减小。2 m/s风速的情况下，粒子最大抬升高度可达95 m，5 m/s风速下粒子最大抬升高度为59 m，10 m/s风速下粒子最大抬升高度为41 m，且风速较大时最大抬升高度变化趋势较为稳定。将污染物中心浓度值衰减至5%时的距离定义为影响半径，图8显示了1 500 m处污染物最大影响半径随时间的变化情况。从图中可以看到，2 m/s时影响半径较大，数值在17～27 m，最大可达27 m；而5 m/s风速时影响半径最大为12 m，10 m/s风速时最大影响半径为7 m。风速的增大，使得影响半径逐渐减小。

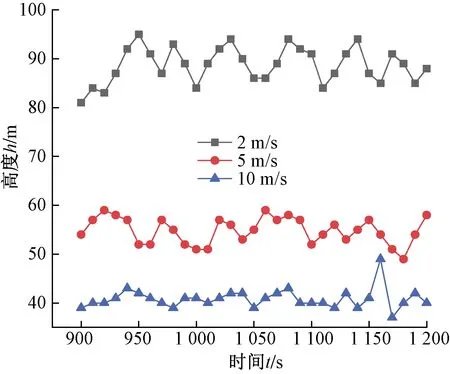
图7 颗粒最大抬升高度-时间变化曲线 Fig.7 The temporal change of the maximum height that can be reached by the elevated particles

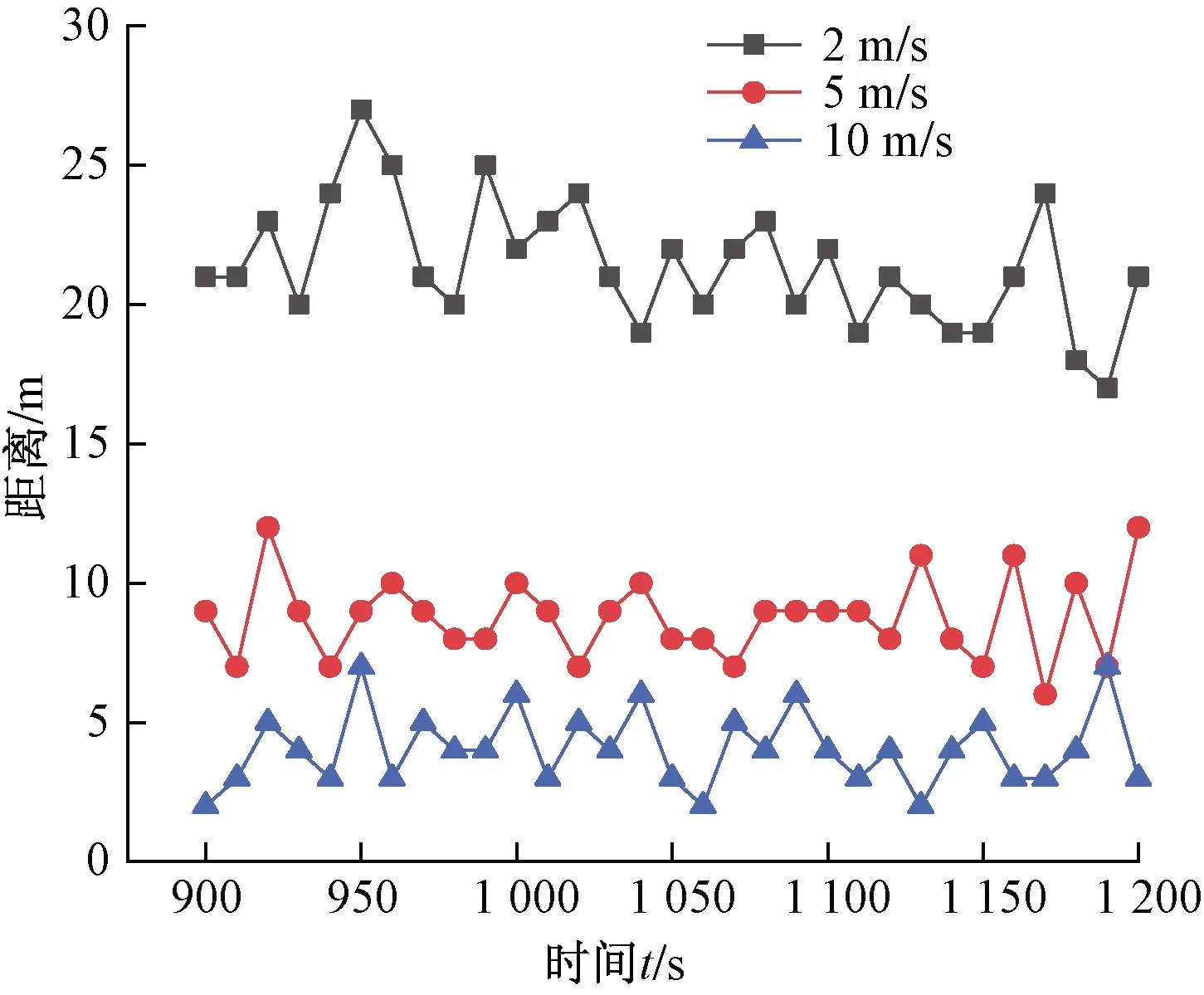
图8 污染物影响半径随时间变化曲线Fig.8 The temporal change of the influencing radius of the pollutants

综合图6、图7、图8分析发现，在入口湍流条件不变的情况下，风速的增大会减小污染物粒子在计算域内的停留时间，由于y方向未设置速度梯度，污染物纵向扩散能力减弱，污染源中心浓度值增大，污染物抬升高度降低，污染物扩散范围较小，即风速增大时，污染物轴向(最大影响半径)径向(抬升高度)扩散都呈现减小的趋势。这一模拟结果，与文献[14]中对单点源烟囱排放的颗粒物扩散的模拟结果相一致。

3 结论

应用MP-PIC方法模拟理想条件下不同风速条件对单点源污染源的污染物浓度时空变化、粒子最大抬升高度、污染物扩散范围的影响，得到如下结论。

(1)MP-PIC方法可以极大地提高计算效率，可以应用于较大尺度的大气污染物扩散模拟。

(2)CFD模拟中污染源对入口风的阻挡作用十分重要。低风速下，受污染源阻挡作用，污染源周边形成方柱绕流现象，污染物在下风方向分裂成为两股，污染物因湍流作用在计算域内波动。2 m/s风速时，分裂的两股污染物之间距离在5～20 m，5 m/s风速时，分裂的两股污染物距离为2～10 m，而风速达到10 m/s分裂状况消失。

(3)风速的增大会减少污染物在计算域内的停留时间，使得粒子移动距离减小，从而导致污染源中心浓度值增大，污染物抬升高度与扩散范围降低。即风速增大时，污染物轴向(最大影响半径)径向(抬升高度)扩散都呈现减小的趋势。