基于灰色熵权模型的城市轨道交通站点运营风险动态评价

刘 兵， 张 彭， 朱广宇*

(1.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.交通运输部规划研究院，北京 100028)

截至2018年底，中国已有35座城市规划建设轨道交通，轨道交通运营总里程达5 766.7 km[1]，预计2020年达到6 200 km，2050年达到11 700 km[2]。随着轨道交通建设规模的不断扩大，轨道交通站点管理和运营的难度也随之增大。城市轨道交通站点作为主要的客流集散场所，站内设施设备专业性强、复杂度高[3]，一旦发生事故，易于造成较大的人员伤亡和财产损失。因此如何及时有效地评估城市轨道交通站点的运营风险对提高其安全管理水平，降低事故发生的可能性具有重要意义。

目前针对城市轨道交通站点运营风险的综合评价已进行了大量研究。王洪德等[4]基于层次分析法对影响城市地铁运营安全的危险因素进行了分析，提出了基于“人-车-轨道-安全管理”的安全运营系统与应急救援相结合的事故预防对策；潘科等[5]基于可拓物元模型对城市地铁线路的运营安全进行了分析，提出了多级可拓地铁运营安全评价方法。马云东等[6]基于OWA-AHP提出了指标权重定量计算的方法，并基于OWA-AHA和熵权法对地铁运营安全进行了综合评价。然而以上研究仅关注了城市轨道交通站点运营安全的静态属性，忽略了时间、环境等因素对评价结果的影响。因此，近年来学者们针对动态评价的方法也进行了深入研究。Verma等[7]基于历史统计经验对时间激励因子进行了量化计算，提出了一类德尔菲法和模糊数学相结合的动态评价方法；黄山松等[8]基于时点权重法对时间激励因子进行了计算，提出了一类灰色动态多指标的评价方法；张发明等[9]基于激励控制线和相对优胜度模型提出了一类“显性-隐性”双重激励作用的动态综合评价方法。

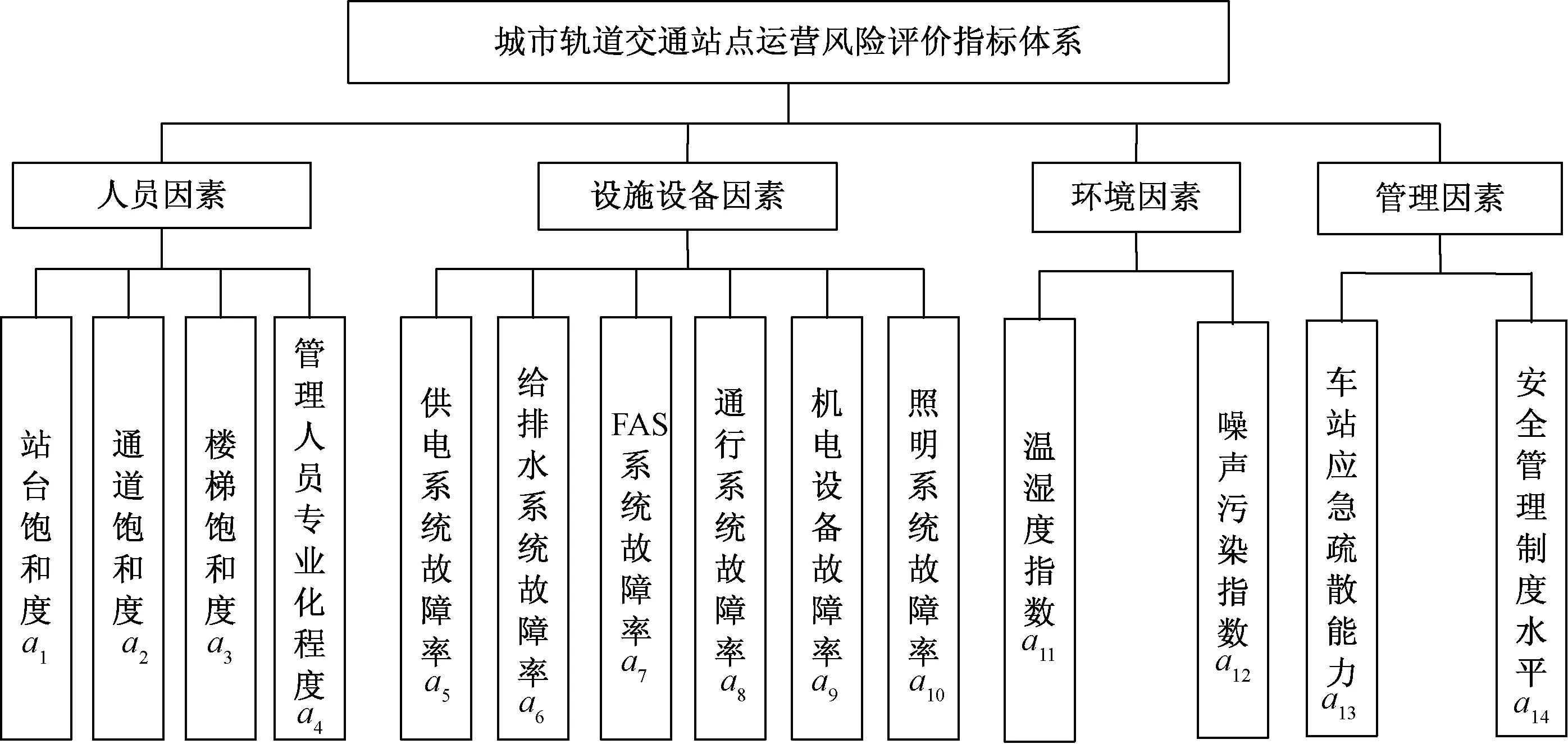
图1 城市轨道交通站点运营风险评价站点指标体系的构建Fig.1 Construction of indicator system for operational risk assessment of urban rail transit station

此类研究为开展城市轨道交通站点运营风险的动态综合评价提供了很好的理论基础，但从这些成果可以看出，目前进行时间激励因子计算的过程中，仍多采用偏好、主观性较强的方式，很少结合原始数据特征对时间激励因子进行科学量化的处理。因此，在当前研究的基础上，基于灰色熵权模型提出一类城市轨道交通站点运营风险动态评价的方法。

1 评价指标体系的构建

结合对系统构成要素和站点历史故障原因的分析，构建城市轨道交通站点运营风险动态评价的指标体系，如图1所示。

2 基于灰色熵权模型的动态评价方法

时间激励因子和指标权重的量化是进行动态评价的关键。时间激励因子反映了当前时间段内城市轨道交通站点的运营风险受前期运营的影响，采取主观赋值的方法难以真实反映城市轨道交通站点运营风险在时间维度上的动态性[10]。因此，通过对评价指标经典域的划分，采用灰色关联度方法对评价指标时间激励因子的计算。同时鉴于主观赋权的随意性，采用灰色熵权模型进行评价指标权重的计算。

2.1 基于灰色熵权法指标权重的确定

熵是对事物“不确定性”程度最好的度量标准，当指标的信息熵越小时，指标蕴含的信息量就越大，所对应的权重也就越高[11]。基于灰色熵权法进行指标权重计算的具体步骤如下。

2.1.1 构建广义灰数评价矩阵并进行标准化

城市轨道交通站点运营风险的动态评价是指通过获取评估站点多个连续时间段内评价指标的实测数据，评估当前时间段站点运营的风险等级。但在实际运营过程中，受外界各种因素的干扰，评价指标的实测数据可能缺失或者获取不完全，呈现出区间灰数的特征。因此，引入广义灰数的概念，构建指标评价值矩阵。

广义灰数是针对多源不确定性系统中信息数据混合运算问题而提出的一种新型不确定数，由模糊集、概率集、灰数集、白数集以及区间模糊集等多种不确定性集合共同表征[12]。m个时间段n个评价指标构成的城市轨道交通站点运营风险评价的广义灰色矩阵可表示为

(1)

对指标同向化处理后，按下式进行标准化处理：

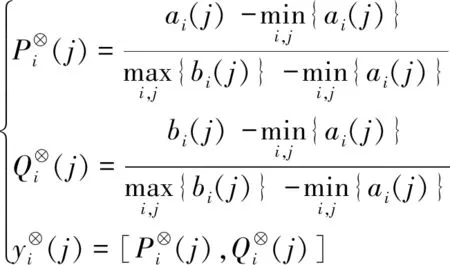
(2)

2.1.2 确定评价指标的灰色熵H⊗(j)

灰数是一个不确定性的数，由灰数计算得到的信息熵即为灰色熵[13]，按下式进行计算：

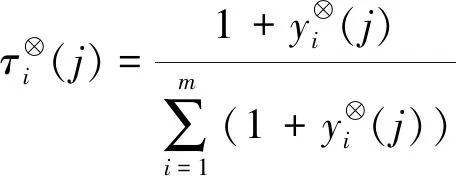
(3)

式(3)中：m为参与评价的时间段个数。

2.1.3 各评价指标灰色熵权的计算

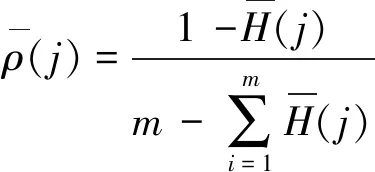
(4)

2.2 时间激励因子的计算

灰色关联度是灰数序列与理想数据列关联性大小的量度，反映了灰数序列与理想数据列发展趋势的相似程度，当理想数据列反映系统主行为的“激励特征”时，相对应的灰色关联度即可反映灰数序列的激励程度。引入灰色关联度方法计算评价指标时间激励因子的具体步骤如下。

2.2.1 确定评价指标体系的经典域

评价指标的经典域是指由风险等级、评价指标和评价指标的量值区间构成的有序三元组[14]。为得到评价指标的经典域，首先需按从高到低的顺序，划分评价指标的风险等级，其次需对轨道交通站点历史运营数据进行统计分析，获取各风险等级下每个评价指标的总量值区间。最后确定的城市轨道交通站点运营风险评价指标体系的经典域为：

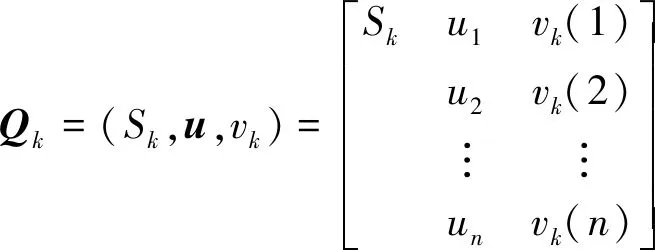
(5)

式(5)中：Sk表示第k个风险等级；u=(u1,u2,…,un)T表示城市轨道交通站点运营风险的评价指标体系；vk(j)表示第j个评价指标在第k个风险等级下总量值区间，vk(j)=[ck(j),dk(j)]，dk(j)、ck(j)分别为第j个评价指标在第k个风险等级下量值区间的上下界。

2.2.2 标准化各风险等级下的经典域

由式(1)可得各风险等级下经典域标准化的形式为

(6)

2.2.3 计算广义灰数评价矩阵和经典域的始点零化像

由一般灰数序列始点零化像的定义[15]可知，广义灰数评价始点零化像为

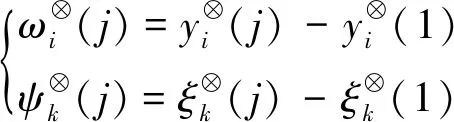
(7)

2.2.4 各时间段下时间激励因子的计算

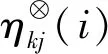
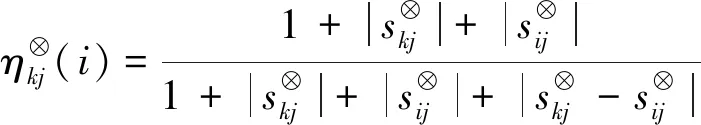
(8)

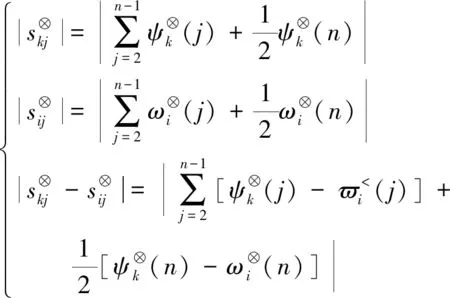
(9)

2.3 确定评估站点的运营风险等级

对评估站点的指标量值按指标维和时间维依次进行加权求和，即可得到各风险等级下第m个时间段评估站点运营风险的综合评价值，取综合评价值中极大值所对应的风险等级作为第m个时间段评估站点的运营风险等级。具体步骤如下。

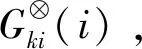
(10)

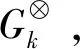
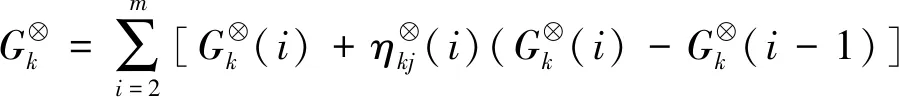
(11)

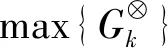
2.4 基于灰色熵权模型城市轨道交通站点运营风险动态评价的基本步骤

步骤1：获取评估城市轨道交通站点第m个时间段内n个评价指标进行量化计算，构建广义灰色评价矩阵，并跟据评估站点历史运营情况，划分评价指标的风险等级，确定经典域；

步骤2：对评价指标的广义灰色评价矩阵和经典域进行同向化、标准化和归一化处理。

步骤3：采用灰色熵权的计算方法，确定评价指标权重。

步骤4：计算广义灰色评价矩阵和经典域的始点零化像，并采用绝对关联度方法，计算m个时间段的时间激励因子。

步骤5：对评估站点m个时间段内评价指标值依次从指标维和时间维进行加权求和，求出各风险等级下评估站点第m个时间段内的综合评价值，进而确定评估站点的运营风险等级。

3 算例分析

通过获取北京市某地铁站点的历史运营数据，参照文献[16]提出的方法对评价指标值进行了量化计算。为了验证本文提出的城市轨道交通站点运营风险动态综合评价方法的适用性，算例中将部分时间段内站台饱和度、楼梯饱和度、供电系统故障率等多个指标的实测数据取为了广义灰数。由此得到评估站点在各时间段内的评价指标值，如表1所示。

将城市轨道交通站点运营的风险按照从高到低的顺序，划分成了5个风险等级，并通过对评估站点历史运营情况的分析，确定了指标经典域的划分规则，结果如表2所示。

根据式(2)～式(4)的计算，得到了评价指标权重值，结果如表2所示。图2给出了评价指标灰色熵权白化的结果。从图2中可以看出，在当前时间段，机电设备故障率、供电系统故障率、安全管理制度水平、楼梯饱和度是影响评估站点运营风险的主要因素。

经式(5)～式(9)的计算，得到了各时间段下评价指标的时间激励因子，结果如表3所示。图3给出了各风险等级下评价指标时间激励因子等权白化的结果，从图3中可以看出，随着时间的增大，评价指标的时间激励因子有增大的趋势。由此可知距离评价时间段越近的时间激励因子对评价结果的激励作用越强，对评价结果的影响更大。

表1 评估站点评价指标值

表2 城市轨道交通站点各指标的经典域和灰色熵权

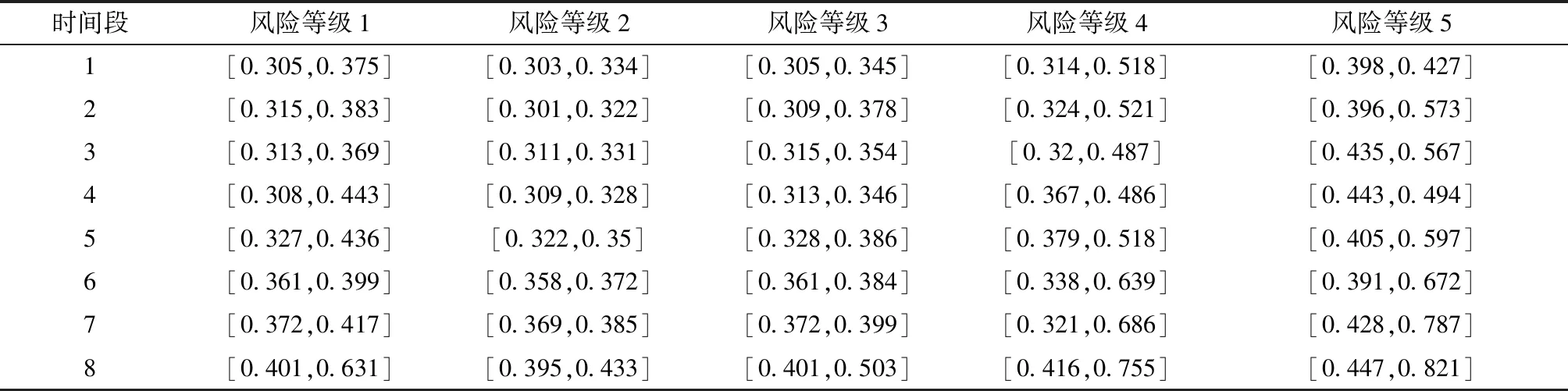
表3 各指标的时间激励因子

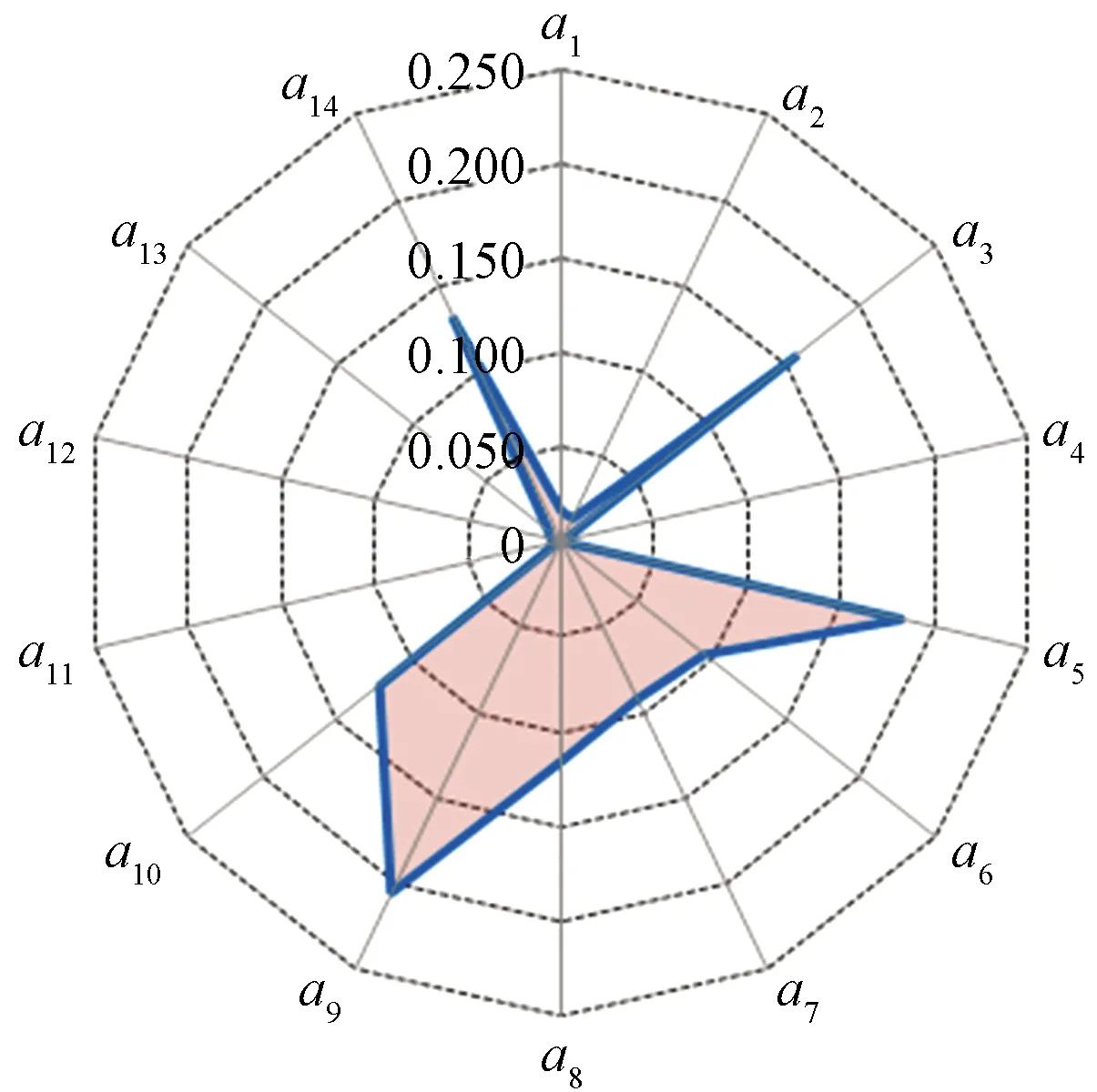
图2 评价指标灰色熵权的等权白化值Fig.2 Value of equivalent whitening for evaluation index

经式(10)～式(11)的计算，得到了各风险等级下城市轨道交通站点运营风险的综合评价值，结果如表4所示。图4给出了综合评价值等权白化的结果，从图4中可以看出，评估站点在第8个时间段内的运营风险等级为第5级。由此可知当前时间段评估站点的运营风险水平较低，安全性较高。

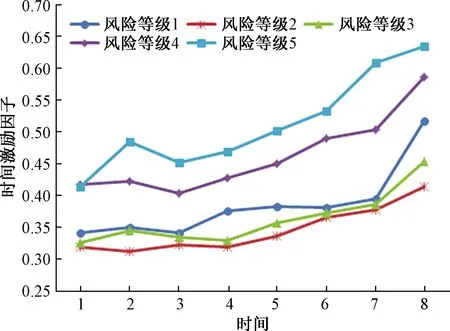
图3 时间激励因子的等权白化结果Fig.3 Results of equivalence whitening for time incentive factor

表4 评价结果

图4 综合评价值的等权白化Fig.4 Equal weight whitening of comprehensive evaluation value

4 结论

通过对城市轨道交通站点运营风险的动态评价展开研究，得到以下结论。

(1)通过对城市轨道交通站点事故致因的分析，从系统构成要素出发，构建了城市轨道交通站点运营风险评价的指标体系。

(2)为弥补当前评价值时间激励因子的不足，结合城市轨道交通站点的运营特性，提出了一类基于灰色熵权模型的城市轨道交通站点运营风险动态评价的方法，运用绝对灰色关联度和灰色熵权模型分别对时间激励因子和指标权重进行了较为客观的计算，并依据物元经典域准确地确定了站点运营的风险等级。

(3)应用所提出的动态评价方法对某地铁站点的运营风险进行了评价。结果表明：当前时间段机电设备故障率、供电系统故障率、安全管理制度水平是影响该站点运营风险的主要因素；该站点在当前时间段的综合风险等级为第5级，站点运营的安全性较高。

(4)结合算例分析可知，该方法在多元不确定性的信息系统中，具有较强的适用性和可行性，能够运用于城市轨道交通站点运营风险的动态评价中。