基于模糊神经网络的城市排水预测

李鹏博， 林汉良

(台湾成功大学都市计划学院,台南 70101)

近年来的快速城市化带来了中国经济的快速发展，促进了地区的协调发展和全社会的进步。与此同时，快速的城市化也带来了新的问题：环境污染和资源短缺，特别是水资源短缺。城市发展的快速扩张模式是不可持续的，会对环境造成破坏。因此，有必要将城市发展模式转变为经济和环境兼顾的集约发展模式。在生态文明建设中，海绵城市的核心是自然积累、自然渗透、自然净化。海绵城市的建设对于容易出现干旱和暴雨的城市具有重要意义。一些严重缺乏水资源的城市在短时间内集中雨量，如何利用这些水资源成为学者关注的议题，而如何更好地预测城市排水量成为一个关键点。

20世纪70年代，许多学者关注城市排水系统水力模型的研究和开发，发展至今几十年已经积累了丰富的经验。目前常用的排水系统水力模型软件主要有英国Wallingford软件公司的 Infoworks ICM软件和美国环保局开发的城市暴雨管理模型(storm water management model，SWMM)。

城市排水系统计算模型中关于排水量的计算主要分为管网汇流和地面径流两部分。在传统的城市排水管网设计和管理中,均采用恒定流水力学理论计算管网的汇流过程,但城市雨、污水管网及合流制管网中的水流是非恒定流,并具有突涨突落的特点。周玉文等[1]开发了一种非恒定流模型，模型可以用于模拟和预报暴雨条件下市区的积水面积和深度。根据模拟计算结果,可以提出改造排水系统的最佳设计方案。祁继英等[2]针对排水系统经历短历时强降雨时产生的波动性问题，将排水系统的传统设计与数学模型有机结合，分析了雨水排水系统的水力学特征。

目前，地面径流的排水设计主要依靠各地的暴雨强度公式对降雨量和降雨强度进行计算。利用这种方式得到的预测数据与实际情况存在较大偏差。张大伟等[3]基于城市暴雨强度公式,应用芝加哥降雨过程线模型,对清华大学的雨水排水系统进行建模分析，给出了一些在排水管道设计方面的建议。卢金锁等[4]对西安市暴雨强度公式进行了修正，采用了高斯-牛顿法等6种优化算法对公式参数进行推导求解；结果表明，新公式关于暴雨强度预测的精度明显优于旧的公式。城市排水系统设计标准偏低,易遭遇超标准暴雨，容易导致暴雨期城市地区地面积水。针对这一问题，徐向阳等[5]建立了城市地面积水数学模型，该模型能够真实地模拟暴雨造成的城市地面积水的涨消过程。

城市排水系统的集成化模拟是国际上推行的一种研究方法。徐速等[6]将SWMM与河流水质模型相结合,构成城市排水系统集成化模拟工具,模型可以实现动态模拟暴雨径流的全过程。李建勇[7]基于Infoworks ICM模型，以上海市杨浦滨江区内的排水系统为例，完整地模拟城市雨水循环过程，利用实测流量数据进行了模型的验证。

传统计算城市排水量的公式推导法在计算过程中进行了大量的简化和假设，由于公式缺乏严谨的证明，参数依赖于历史数据和经验等一系列原因，使得预测结果不甚理想。同时，恒定流水力学理论的计算方法，无法适用于预测城市水流的突涨突落的特点。基于系统集成化模拟和海绵城市的概念，针对城市排水的波动性和非线性特征，提出一种基于模糊神经网络预测的城市排水预测算法，通过神经网络自我学习的机制，采用灰色模型构建城市排水预测模型，建立城市排水量预测回归函数。

1 城市排水系统

海绵城市建设的背景下，如何预测城市排水量成为关键点。城市排水系统如图1所示，计算模型主要分为两部分，城市生活、工业用水流入的管道汇流，还有降雨量造成的地面雨水径流。

图1 城市排水系统Fig.1 Urban drainage system

1.1 海绵城市

海绵城市建设应遵循生态原则，结合自然环境恢复与人工措施，在确保城市排水和防涝安全的前提下，最大限度地发挥城市对雨水的蓄积、渗透和净化等作用，促进雨水资源的再利用，提升生态环境[8]。海绵城市的建设不是要替换传统的排水系统，而是对城市排水系统的支援和辅助。在海绵城市的建设中，有必要整体规划自然降水、地表水和地下水的系统性，协调供水和排水，以及水循环利用的其他方面，并考虑其复杂性和长期性。

中国海绵城市建设的时间表已经明确，只能推进，不可推迟。全国130多个城市制订了海绵城市建设方案。核心目标是通过建设海绵城市，在现场利用70%的降雨量。为实现这一目标而制订了时间表，2020年，20%的城市建成区满足这一要求，到2030年，城市建成区的80%必须达到要求。

1.2 城市高压排水系统

高压排水泵组位于绿色公共建筑13层的横向通道中。根据《给水排水设计手册,第五册:城镇排水》[9]，排水管道的流量计算公式为

Q=Av

(1)

(2)

式中：Q为排水管道的流量，m3/s；A为水流有效断面面积，m2；v为水流断面的平均流速，m/s；R为水力半径，m；I为水力坡度，采用排水管的坡度；n为粗糙系数。

排水管的水头损失是使用基于所述管段的不同流的达西公式[10]计算分段。其计算公式为

(3)

式(3)中：hf为水头损失，m；λ为水头损失系数；L为管道长度，m；D为管道内径，m；V为管道流速，m/s；g为重力加速度，m/s2。

1.3 雨水排水系统

在排水管网设计中,为了确定雨水管渠的尺寸和坡度,必须首先确定管渠的设计流量,而雨水管渠的设计流量主要取决于地区的降雨强度。降雨计算采用以下暴雨强度公式[9]：

(4)

t=t1+mt2

(5)

式中：q为设计的降雨强度，L/(s·hm2)；A1为重现期为1 a的设计雨力参数；C为雨力变动参数；T为设计降雨重现周期，a；b为降水历时修正参数；n为暴雨衰减指数；t为降雨持续时间，min；t1为地面集水时间，min；t2为管道内通行时间，min；m为管道中的雨水流量时间的延迟系数。

设计的雨水流量：

Q=ψqF

(6)

式(6)中：Q为设计的雨水流量，m3/s；ψ为径流系数；F为流域面积，hm2(1 hm2=104m2)。

2 基于模糊神经网络的排水特征量化

TS(Takagi-Sugeno)模糊模型最早由Takagi和Sugeno[11]两位学者在1985年提出。该模型的主要思想是将非线性系统用许多线段相近地表示出来，即将复杂的非线性问题转化为在不同小线段上的问题。将T-S模型与通常的模糊神经网络的分析结构有机地结合，得到多输入单输出条件下的T-S模糊神经网络结构，如图2所示,由前件网络和后件网络组成[12-14]。

图2 T-S模糊神经网络结构Fig.2 T-S fuzzy neural network structure

2.1 前件网络

第1层是输入层，输入值x=(x1,x2,…,xn)T,该层中的节点数量为n。

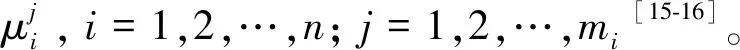
mi是xi的模糊分区数,其中隶属函数使用高斯函数表示为

(7)

第3层是模糊规则层，其作用是匹配模糊规则的前提并计算每个规则的适用性。也就是说，模糊运算符用作连续乘积运算符。

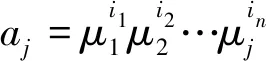
(8)

第4层中的节点数量与第3层中的节点数量相同，并且它实现了归一化计算以避免在学习过程中由过度校正参数引起的振荡。该层的公式表示为

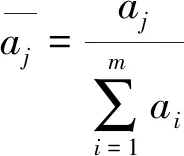
(9)

2.2 后件网络

第1层是输入层，其中0号节点的输入值x0=1的作用是提供模糊规则结果的常数项。

第2层有m个节点，其作用是计算每个规则的后果。

(10)

式(10)中：k=1,2,…,n;j=1,2,…,m。

第3层完成系统的输出计算，即

(11)

可以看出，y是所有规则的后果的加权和，其权重系数是每个模糊规则归一化后的适用度，即前件网络的输出作为结果的第3层。

2.3 学习算法

2.3.1 误差计算

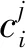
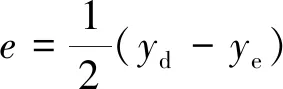
(12)

式(12)中：yd是网络的预期输出;ye是网络的实际输出;e是预期产出与实际产出之间的误差。

2.3.2 系数校正

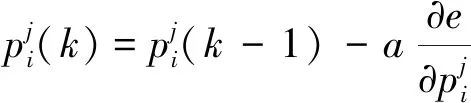
(13)

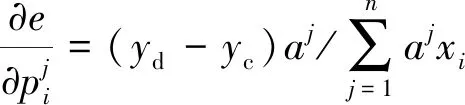
(14)

2.3.3 参数校正

(15)

(16)

式(15)和式(16)分别是隶属函数的中心和宽度。

3 实验分析

3.1 广州市排水数据收集

以广州市为例，对城市排水量的影响因素进行分析。根据广州市统计局官方数据，初步选取工业总产值x1、工业用水费x2、农林牧渔业总产值x3、降水量x4、国内水价x5、城市总人口x6、市政排水价格x7、城市人均居住面积x8作为影响城市排水的因素。城市排水量y为预期的预测值。收集的数据如表1所示。通过多变量回归分析城市排水的影响因子，得到表2所示的结果。

通过表2分析可得，城市总人口x1、降水量x4、生活用水价格x5和总人口x6被选为预测城市排水的影响因子，构成新的样本组。

3.2 城市排水预测结果

在T-S模糊神经网络的基础上对其进行了算法改进，将灰色模型用于城市排水预测，建立回归预测目标函数。鉴于城市排水量突涨突落的波动性特征，将灰色模型数据与三次指数平滑法结合进行实时分割，通过设置分割点的方法用于建立滑动窗口，通过构造误差预测序列来确定分割点，以提高检测过程的鲁棒性。

指数平滑算法可以对同时含有趋势和季节性的时间序列进行预测，所有先前的观测值都对当前平滑值产生了影响，指数平滑法的基本公式为

St=ayt+(1-a)St-1

(17)

式(17)中：St为时间t的平滑值；yt为时间t的实际值；St-1为时间t-1的平滑值；a为平滑常数，其取值范围为[0,1]。

在MATLAB 2014b中运行T-S模糊神经网络模型。将选取的预测城市排水量的影响因子，即城市总人口x1、降水量x4、生活用水价格x5和总人口x6输入到模型中，通过收敛得到城市排水量的预测数据。

为了对比不同算法预测的准确性和运行的性能，分别采用支持向量机、灰度支持向量机和预测算法对广州市2004—2014年的城市排水量进行预测，获得的预测结果如图3所示。

图3表明，与几种算法相比，本研究提出的算法优于其他3种选择对比算法。T-S模糊神经网络预测算法优于支持向量机算法和灰度支持向量机算法。随着灰度支持向量机算法的灰度改进方法的增加，其算法性能优于简单的支持向量机算法。预测性能比较如表3所示。

表3表明，本文提出的算法在运行时间方面具有最小均方根误差，明显优于其他3种对比算法，表明了该算法在计算精度和运行效率方面的优势。

4 结论

基于T-S模糊神经网络模型，提出改进的城市排水量预测算法。将灰色模型用于城市排水预测，建立回归预测目标函数。将灰色模型数据与三次指数平滑法结合进行实时分割，通过设置分割点的方法用于建立滑动窗口，得到数据的实时统计特性。

尽管本研究在数据方面存在一些限制，但成功地将模糊神经网络模型应用在城市排水量预测方面。在T-S模糊神经网络模型的基础上，针对城市排水量突涨突落的波动性和非线性特征，通过设置分割点和结合指数平滑法，对城市排水量的预测算法进行了改进。模拟结果很好地预测了城市排水量的波动性和非线性特征。

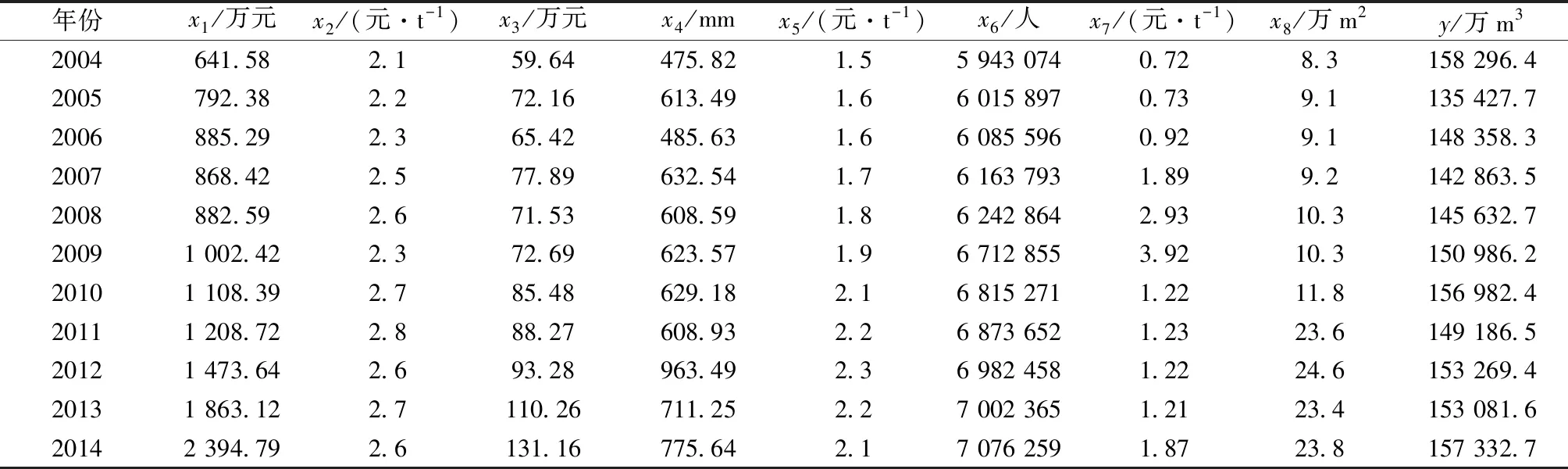
表1 城市排水数据收集

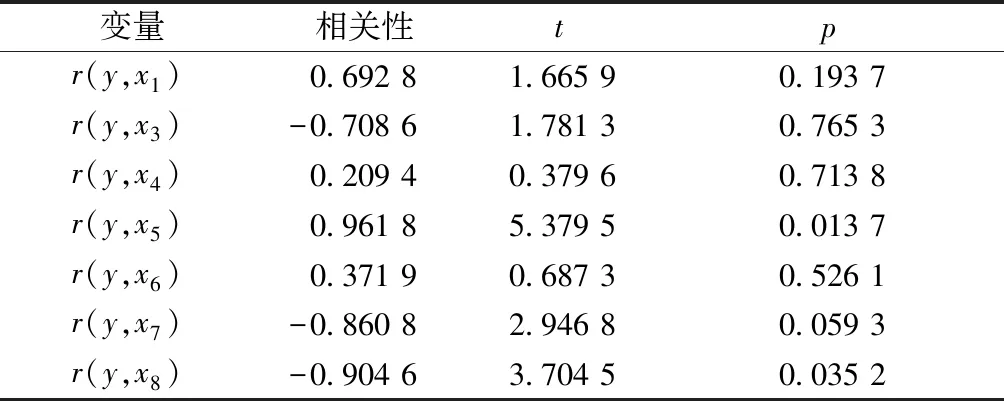
表2 影响因子的多变量回归分析结果

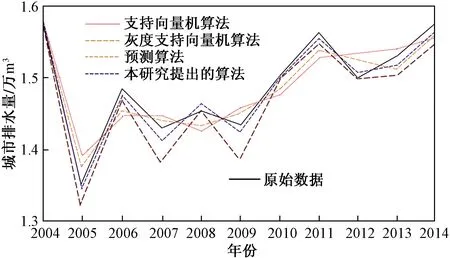
图3 预测结果的比较Fig.3 Comparison of prediction results

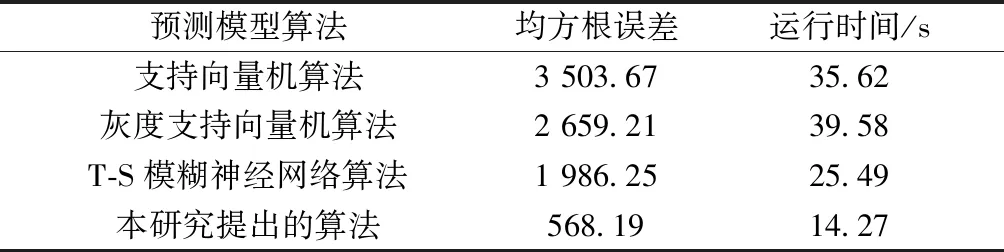
预测模型算法均方根误差运行时间/s支持向量机算法3 503.6735.62灰度支持向量机算法2 659.2139.58T-S模糊神经网络算法1 986.2525.49本研究提出的算法568.1914.27

通过城市排水预测模拟实验，对比不同算法的预测精度和运行性能表明，本研究提出的算法在准确度和运行时间方面均优于其他3种算法，能够有效提高城市排水的预测精度和预测效率，更好地反映了整体趋势。