考虑楼板效应的钢框架结构连续倒塌分析

郑文豪

(北京市市政工程设计研究总院有限公司 100082）

引言

连续倒塌是指建筑结构在爆炸等非常规荷载作用下， 由于局部损坏的扩展导致结构发生较大的破坏甚至整体倾覆性倒塌[1]。 随着连续倒塌事件的频繁发生， 国内外学者纷纷对连续倒塌展开了研究。 文献[2]推荐采用静力线弹性计算方法。但静力线弹性分析不能真实地反映结构连续倒塌时的动力非线性效应， 使得计算结果偏不安全，为了较准确地模拟结构连续倒塌过程， 建议采用动力非线性计算方法[3，4]。 文献[5]对钢筋混凝土框架结构抗连续倒塌设计方法进行了研究， 基于非线性动力分析的拆除构件设计法进行分析的基础上， 对基于线弹性静力分析的拆除构件法的原理和设计参数进行了分析和验算， 提出适合我国工程结构的设计参数。 文献[5，6]对一榀底层中柱失效的多层平面钢框架进行连续倒塌仿真分析。 当具体对结构进行动力分析时， 常采用抽柱法对结构进行抗连续倒塌分析设计[7]。 而抽柱法中失效时间的长短对结构的动力效应影响较大，故选取一个合理的失效时间至关重要。 文献[8]基于单榀钢框架进行详细的连续倒塌分析， 研究了底层柱失效时间对结构响应的影响和竖向荷载传力路径以及梁的受力机理。

鉴于目前对于钢框架连续倒塌动分析较少，动力分析大部分失效时间及失效位置不明， 并且基本均为单榀结构或纯框架结构的情况。 为探究楼板对钢框架结构抗连续倒塌性能的影响， 本文在考虑楼板效应的基础上对空间框架结构进行了抗连续倒塌分析， 从失效时间、 失效位置、 抗力提高系数的角度进行了对比分析， 为抗连续倒塌设计提供一定参考。

1 工程实例及有限元模型

1.1 工程实例

北京大兴区某员工宿舍， 钢框架结构， 首层层高 4.2m， 2 层 ～6 层层高 3.2m， 平面布置如图1 所示。 采用压型钢板组合型楼板， 如图2 所示。 组合楼板截面相关参数见表1。 压型钢板采用 YX-120 -230 -690(II） -2.3。 楼面、 屋面恒荷载分别为 4.5kN/m2、 5.0kN/m2； 楼面活荷载 2.5kN/m2， 上人屋面活载 2.0kN/m2。 墙体均采用 390mm ×190mm ×190mm 混凝土空心小砌块。 建筑场地类别为Ⅱ类， 抗震设防烈度8 度，设计地震基本加速度值为0.20g。 基本风压W0=0.45kN/m2， 地面粗糙度为 B 类。 钢材采用Q345B， 混凝土强度为C30。

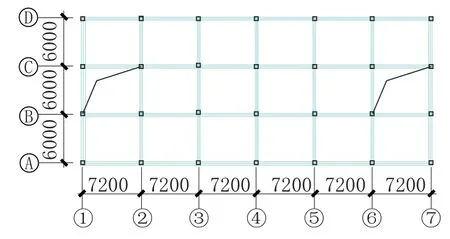
图1 平面布置示意图(单位： mm)Fig.1 Plane layout of structure (unit: mm）

图2 组合楼板组成Fig.2 Composition of composite floor

表1 组合楼板截面参数Tab.1 Sectional parameters of composite floor

1.2 有限元模型

基于ETABS 软件对钢框架结构进行连续倒塌分析， 组合楼板采用ETABS 中组合楼板deck单元进行模拟。 deck 单元可以用于模拟压型钢板+后浇混凝土面层楼板， 此单元仅有membrane性质且单向传力， 在建模时的箭头方向即板的传力方向， 充分利用etabs 中对组合楼板模块这一特性， 按照YJK 压型钢板的相关参数对etabs 中组合楼板定义。 应用YJK 对本结构进行抗震设计。 选用 Q345B 钢材， 梁截面采用 H500 × 300 ×10 ×16， 柱截面采用箱形截面首层为□500 ×500×20， 2 层 ～5 层为□400 ×400 ×20， 底层柱脚、梁柱节点均刚接。 计算结果满足多遇地震作用下弹性层间位移角、 罕遇地震作用下弹塑性层间位移角变形控制条件， 并符合二级框架抗震设计各项指标要求。

基于ETABS 软件对钢框架结构进行动力连续倒塌分析， 组合楼板采用ETABS 中组合楼板deck 单元进行模拟。 梁两端布置M3 塑性铰， 柱梁端布置P-M2 -M3 铰来体现结构的非线性行为。 分别建立空间纯框架及含楼板空间框架模型， 如图 3 所示。

图3 ETBAS 有限元模型Fig.3 ETBAS finite element model

2 抗连续倒塌分析理论

结构连续倒塌分析方法主要有[3]: 局部抵抗偶然荷载设计法(Specific Local Resistance Method）和抽柱法。 其中， 抽柱法是当前应用最为广泛的分析方法。 通过在规定的较短时间内对结构某构件进行失效处理， 然后去分析研究剩余结构的反应[9]， 从而达到对结构抗连续倒塌性能进行评估的目的。

2.1 抽柱位置

采用抽柱法模拟构件失效状态， 分别对GSA2003 中建议的角柱、 边柱及内柱三种结构构件失效状态进行模拟。 其中抽柱对象均为首层柱， 抽柱位置如图4 所示。

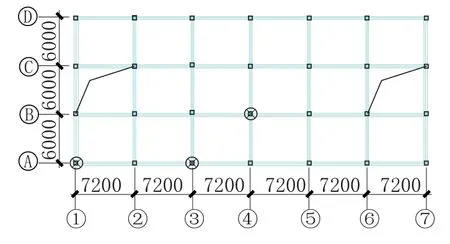
图4 抽柱位置示意图Fig.4 Schematic diagram of column drawing position

2.2 荷载组合

拆除构件法分为线性静力、 非线性静力、 线性动力、 非线性动力等几种分析方法。 GSA2003推荐的静、 动力分析法荷载组合公式如下:

3 抗连续倒塌分析

在连续倒塌中， 关键构件的破坏位置及失效时间直接关系到剩余结构在荷载作用下的响应，故对两结构分别从不同失效位置、 不同失效时间角度来探究楼板对钢框架结构抗连续倒塌能力的影响。

3.1 失效时间对结构的影响

以文献[9]推荐的几种失效时间: 1ms、10ms、 1/10 剩余结构竖向振动周期 (T2/10）、100ms、 1/10 剩余结构基本自振周期 (T1/10）、T2、T1分别对两结构进行不同工况下连续倒塌模拟， 得到不同失效时间下失效位置竖向位移时程曲线。

1.角柱失效工况

由图5 可见， 失效时间的长短对结构动力响应影响显著， 失效时间越短结构的动力响应越明显。 角柱失效后， 振动响应逐渐衰弱， 失效处节点位移随着时间逐渐趋于稳定。 纯框架结构在1ms、 10ms、T2/10 及 100ms 失效时间下， 动力响应基本一致， 也最为强烈， 失效处竖向最大位移可达 52mm 左右。 纯框架结构在 1ms、 10ms、T2/10 及100ms 失效时间下， 动力响应均比较强烈且竖向最大位移比较接近， 失效节点竖向位移最大值达46mm。 楼板的存在使结构在角柱失效后竖向位移有一定程度的减小。

纯框架结构在失效后2s 时结构动力响应基本趋于稳定， 而含楼板结构在1.3s 时结构的动力响应已经基本趋于稳定状态， 楼板的存在使结构在构件失效后能较快地趋于稳定状态。 失效时间对有、 无楼板剩余结构动力响应影响均比较显著， 失效时间T2/10 基本能反应结构在角柱失效后的动力响应状态， 当失效时间为T1时， 两结构动力响应均有明显减小。

图5 角柱失效竖向位移时程曲线Fig.5 Time history curve of vertical displacement due to corner column failure

2.边柱失效工况

由图6 可知， 边柱失效情况下纯框架结构与含楼板结构的竖向时程位移有较大区别。 纯框架结构在边柱失效后振动响应比较明显， 含楼板结构振动较微弱。 随着失效时间的增加， 纯框架结构竖向位移逐渐减小， 并且这一较小作用随失效时间增长表明比较明显。 对于含楼板结构失效时间的长短对结构失效位置处竖向位移基本无影响。

图6 边柱失效竖向位移时程曲线Fig.6 Time history curve of vertical displacement due to side column failure

纯框架结构竖向最大位移为62mm， 含楼板结构最大竖向位移为30.2mm， 可见在边柱失效情况下， 楼板对结构抗连续倒塌能力改善较角柱失效情况更为明显。 同时由图6 可见，T2/10 基本能够表征结构边柱失效下的结构振动响应， 这一点同角柱失效情况。

3.内柱失效工况

由图7 可见， 内柱失效工况下， 纯框架结构与含楼板结构不同失效时间下失效位置竖向位移差异非常明显。 纯框架结 构在 1ms、 10ms、T2/10、 100ms、T1/10 失效时间下， 结构的振动响应基本一致， 最大竖向位移为86mm。 当失效时间为T2、T1时， 纯框架结构失效处竖向位移明显随着失效时间增长而减小。 含楼板结构在不同失效时间下结构的竖向位移并没有区别， 并且楼板基本无振动响应。 这是由于含楼板结构因楼板的存在， 提高了结构的完整性， 使结构能在更为短的时间内完成新的内力分配。 含楼板结构最大竖向位移稳定为36mm， 可见楼板能有效降低失效处竖向位移， 从而提高结构抗连续倒塌能力。

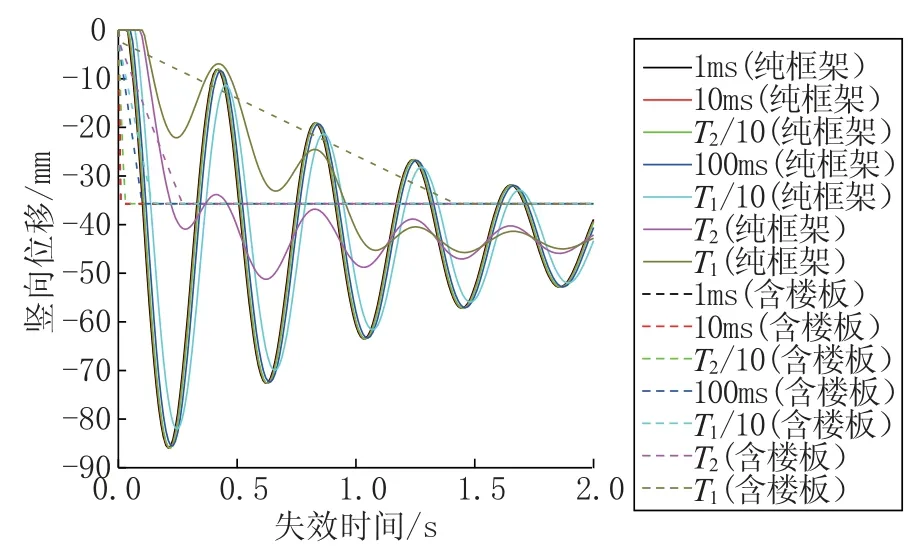
图7 内柱失效竖向位移时程曲线Fig.7 Time history curve of vertical displacement due to internal column failure

3.2 抗力提高系数

本文以失效点在动力非线性分析下的最大竖向位移Ud与静力线弹性分析(与动力非线性分析采用相同的荷载及荷载组合）的竖向位移US的比值(抗力提高系数R=Ud/US）作为动力效应指标。通过计算可得角柱失效、 边柱失效及内柱失效三种情况下抗力提高系数R与失效时间Δt之间的关系。 其 中 时 间 分 别 取 1ms、 10ms、T2/10、100ms、T1/10、T2、T1。

1.角柱失效工况

由图8 可见， 角柱失效情况下纯框架结构与含楼板结构抗力提高系数均小于2， 并且随着失效时间的增加， 动力放大系数逐渐减小。T2/10 为失效时间的情况下， 结构位移放大系数为最大值， 进一步说明T2/10 作为失效时间可反应结构在构件失效下的最大动力响应。 当失效时间为T1时， 两结构的抗力提高系数均接近1， 表明此时动力分析的竖向位移与静力分析位移较为接近。

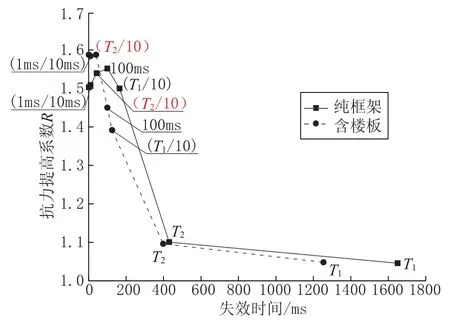
图8 角柱失效抗力提高系数Fig.8 Improvement coefficient of corner column failure resistance

2.边柱失效工况

由图9 可见， 边柱失效情况下纯框架结构与含楼板结构抗力提高系数均小于2， 并且随着失效时间的增加，R逐渐减小。 纯框架结构位移动力系数最大值为1.7， 最小值为1.08。 而含楼板结构的R最大值为 1.025， 最小值为 1.014， 基本为1 附近。 由此可见忽略楼板的作用大大低估了结构抗连续倒塌能力。

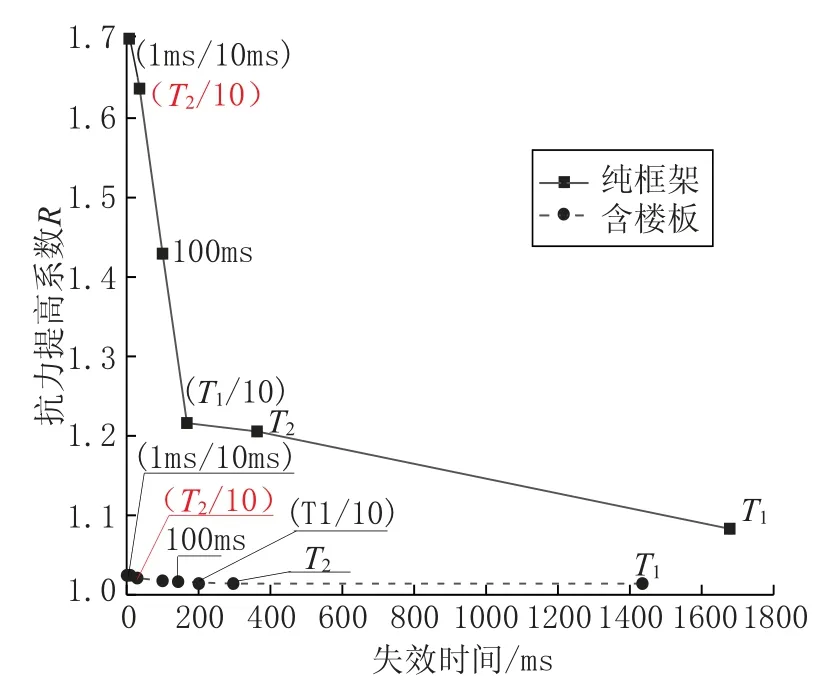
图9 边柱失效抗力提高系数Fig.9 Improvement coefficient of side column failure resistance

3.内柱失效工况

由图10 可见， 内柱失效情况下纯框架结构与含楼板结构抗力提高系数均小于2， 并且随着失效时间的增加，R值逐渐减小。 纯框架结构位移动力系数最大值为1.9， 最小值为1.03。 而含楼板结构的R最大值为1.005， 最小值为1。 可见内柱失效情况下， 楼板对结构抗连续倒塌能力影响也相当明显。

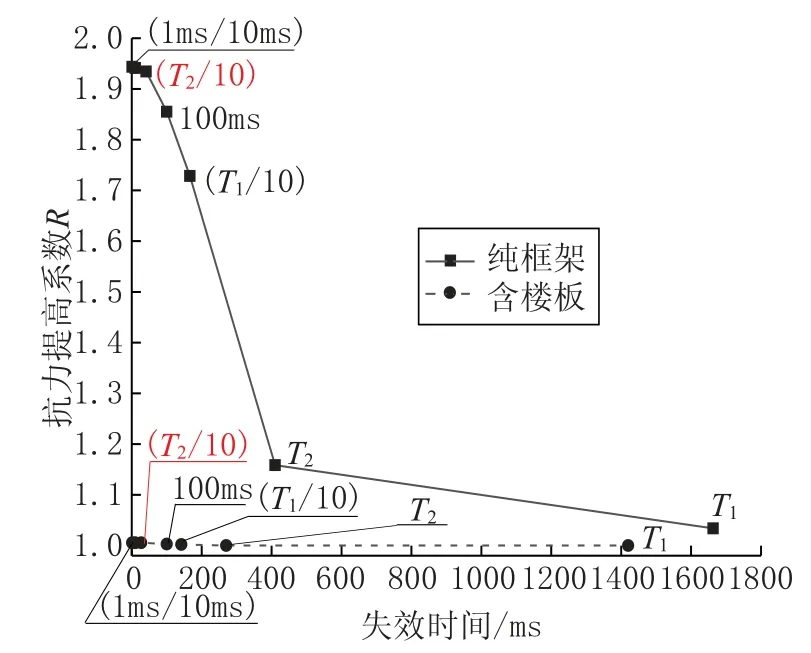
图10 内柱失效抗力提高系数Fig.10 Improvement coefficient of internal column failure resistance

综上所述， 在角柱失效情况下， 楼板对结构竖向抗力提高系数改善不明显。 在边柱失效及内柱失效情况下， 抗力提高系数改善相当明显。 连续倒塌研究中， 楼板的忽视会大大低估结构的抗连续倒塌能力。 同时通过R可知， 在失效时间较短时， 动力响应均比较强烈， 这时在连续倒塌分析时， 应以动力分析为主。 随着失效时间的增长， 抗力提高系数逐渐趋于1，故在较长的失效时间情况下， 动力响应与静力响应比较接近， 这时可采用静力分析方法代替动力分析法。

3.3 竖向传力路径

由以上分析， 以T2/10 为失效时间， 分别对角柱失效、 边柱失效及内柱失效三种情况下失效位置附近构件内力及位移变化进行研究。 为清楚表示失效处研究对象， 取失效处一榀结构如图11所示。

1.角柱失效工况

分别取2 层柱C1 轴力、 首层柱C2 轴力及梁B24 弯矩为研究对象， 其内力时程曲线如图12所示。

由图12 可知， 角柱失效后失效处上方柱C1轴力在较短时间内下降为0 左右， 失效处相邻柱C2 内力增加， 并逐渐趋于稳定。 梁B24 在角柱失效后形成悬臂梁， 在较短的时间内弯矩有大幅度的增加， 随着失效后时间增长， 内力逐渐趋于稳定。 纯框架结构内力波动明显大于含楼板结构。

图11 失效处框架编号Fig.11 Frame number of failure position

图12 角柱失效内力时程曲线Fig.12 Time history curve of failure internal force of corner column

2.边柱失效工况

分别取2 层柱C9 轴力、 首层柱 C10 轴力及梁B44 弯矩为研究对象， 其内力时程曲线如图13所示。

由图13 可知， 边柱失效后， 纯框架结构柱C9 内力迅速较小， 在0 值附近轻微波动， 含楼板结构在较短的时间内将为0， 构件退出工作。首层柱C10 在较短时间内轴力由大幅度的增加，纯框架结构的增幅比较明显， 随着失效时间的增长， 纯框架结构C10 轴力逐渐趋于稳定。 含楼板结构在边柱失效后， 首层柱C10 在较短的时间内增到4300kN 后基本稳定在这一值； 边柱失效后纯框架结构梁B44 有较大幅度的波动， 含楼板结构弯矩相对比较稳定， 在194kN·m 附近轻微波动。 由这三个构件内力图可知， 楼板增加了结构的整体性， 使在边柱失效后更短的时间内完成新传力路径的形成。

3.内柱失效工况

分别取2 层柱C14 柱轴力、 首层柱C15 轴力及梁B11 弯矩为研究对象， 其内力时程曲线如图14所示。

由图14 可以看出内柱失效后， 柱C14、 C15及梁B11 内力呈现趋势基本与边柱失效一致。 楼板的提高结构稳定作用在内柱失效情况下更加明显。 这是由于不同于角柱失效， 在边柱及内柱失效时， 楼板与相邻梁与柱之间存在“拉结”作用，使在关键构件失效后仍能在较短的时间内完成力的传递。 角柱失效楼板形成“悬臂端”， 故在角柱失效情况下， 纯框架结构与含楼板结构内力变化时效比较一致。

图13 边柱失效内力时程曲线图Fig.13 Time history curve of failure internal force of side column

图14 内柱失效内力时程曲线Fig.14 Time history curve of internal force due to internal column failure

4 结论

为探究楼板在结构连续倒塌中的作用， 基于抽柱法对角柱失效、 边柱失效及内柱失效三种工况进行了连续倒塌模拟， 通过对比不同失效位置工况下失效位置竖向位移及抗力提高系数， 得到以下主要结论:

1.纯框架失效时间越短结构的振动响应越明显， 含楼板结构仅在角柱失效工况下失效时间对结构振动响应有较明显影响。 两结构1/10 竖向振动周期均能较好地表征结构失效下的动力响应状态， 故建议抗连续倒塌分析研究中可以1/10竖向振动周期为失效时间。

2.楼板能有效降低结构失效位置处竖向位移， 提高结构抗连续倒塌能力。 忽略楼板作用可能导致低估结构抗连续倒塌能力。 楼板对结构抗倒塌能力的改善作用在边柱失效及内柱失效情况下更加明显。

3.通过对比抗力提高系数可知， 当失效时间较短时应以动力分析为主研究结构的连续倒塌能力， 当失效时间较长， 动力分析与静力分析结果基本一致， 这时可以静力分析代替动力分析来表征结构动力响应。

4.楼板加速结构新传力路径的形成， 提高了结构整体稳定性， 提高了结构的抗连续倒塌能力。