地下连续墙锚碇基础在开挖过程中性能分析*
程晔 袁鹏 陈旭浩 过超
(1.南京航空航天大学土木与机场工程系 210016;2.江苏省机场基础设施安全工程研究中心 南京210000; 3.朗诗绿色集团 南京210004;4.中交公路规划设计院有限公司 北京100088)
引言
地下连续墙由于其良好的工作性能, 已被广泛应用于高层建筑、 地铁车站、 地下变电站等大型基坑工程中。
目前国内外学者对地下连续墙作为支护结构在基坑工程中的应用作了大量的研究, 孙学先[1]、 姜涛[2]分别从现场模型实验和数值模拟的角度对地下连续墙在施工过程中承载力和荷载传递的机理进行了研究; 丁勇春[3]通过对基坑工程中地下连续墙试验槽段进行现场监测, 发现土体侧移和地表沉降值随槽段开挖深度的增加而增大, 且土体侧移主要发生在软土层; Clough 和O'Rourke[4-6]通过对不同类土中的墙体径向位移与基坑最大开挖深度之间的关系进行研究, 得出墙体径向位移与抗隆起安全系数、 支护体系的刚度、 支撑的平均间距之间的联系。 Karlsrud[7]通过对奥斯陆(Oslo, 挪威首都)软粘土基坑开挖进行研究, 提出更为详细的抗隆起安全系数与变形的关系。 Ou[8]等通过对台北软粘土中的10 个抗隆起安全系数均较高的基坑进行研究, 得到墙体最大水平位移与基坑开挖深度的比值, 并与Peck[9]预估图表计算出的结果进行比较。
由于圆形地下连续墙具有拱效应, 在开挖过程中对比矩形形式能更好地控制变形[10]。 因而在桥梁工程中, 圆形的地下连续墙开始应用于锚碇基础。
润扬长江大桥北锚碇[11]为采用地下连续墙加内撑的结构形式, 其底部嵌入微风化的粗粒花岗闪长岩, 李劭晖、 徐伟[12]通过数值模拟计算,发现地下连续墙在嵌岩面上的负弯矩主要和地下连续墙的嵌岩深度有关, 并根据计算结果和施工实践提出了不同岩层时所需的嵌岩深度。 阳逻长江大桥[13]、 鹦鹉州长江大桥[14]、 珠江黄埔大桥[15]均为圆形地下连续墙加内衬的支护结构形式, 其底部分别嵌入砂砾岩、 微风化白云质灰岩以及弱风化砾岩。 李劭晖[16]以阳逻大桥南锚碇为研究背景, 通过现场实测变形, 以有限元软件ANSYS 对土体的m值进行反分析, 预测墙体的变形, 为开挖时施工的安全性提供了理论依据;王琨, 张太科[17]等针对珠江黄埔大桥南汊悬索桥南锚碇的支护特点, 利用有限单元法对其施工过程进行了仿真分析, 并与现场监测结果进行对比,结果表明施工过程中圆形嵌岩地下连续墙的拱效应显著, 能够有效减小墙体竖向应力、 径向位移。
综上所述, 目前的研究中地下连续墙应用于常规基坑工程十分注重监测和反演分析。 但是将其应用于锚碇基础的工程实例还较少, 对于锚碇基础采用嵌入软岩的地下连续墙作支护结构, 且不设内部支撑的工程, 缺乏相关的监测和分析。本文针对虎门二桥泥州水道桥西锚碇工程, 对开挖过程中地下连续墙的径向位移、 墙外土压力等进行实时监测, 并与数值模拟的结果进行对比分析。
1 工程概况
虎门二桥是广东省高速公路网规划中连接广州和东莞的重要东西向通道, 全线为桥梁工程,总长12.89km, 为标准的八车道高速公路, 共设置两座跨江大桥, 其中泥州水道桥为(548 +1688)m 的双塔双跨钢箱梁悬索桥, 其西锚碇采用重力式圆形锚碇基础。
1.1 工程地质与水文条件
西锚碇(图1)位于番禹区海鸥岛沙南村境内, 距坭州水道西岸约100m, 地貌为珠江三角洲平原类型, 区域覆盖层主要由第四系全新统海陆交互相淤泥质土、 砂土和第四系更新统冲击相粉质粘土、 砂土、 圆砾土组成; 基底为白垩系白鹤洞组(K1b)泥岩, 存在风化不均匀、 风化夹层现象, 中风化泥岩饱和单轴抗压强度为5.06MPa~9.49MPa, 微风化泥岩饱和单轴抗压强度为10.38MPa ~ 19.79MPa, 属极软岩 - 较软岩。 各土层分布见表1。
地下水类型以第四系松散层孔隙承压水及基岩裂隙水为主, 水位埋深较浅, 稳定在0.5m左右。

图1 虎门二桥西锚碇基础构造示意Fig.1 Structure of the west anchorage foundation of Second Humen Bridge

表1 各层土的参数Tab.1 Parameters of soil profile
1.2 施工工艺与支护体系
西锚碇的地下连续墙为外径 90m, 壁厚1.5m 的圆形结构; 施工槽段分 I 期和II 期两种各30 个槽段(图2); 锚碇区岩石饱和单轴抗压强度较低、 基岩破碎、 裂隙发育, 为避免地下连续墙底脚发生渗流及踢脚破坏, 墙体嵌入中风化泥岩3m ~4m。
西锚碇区内衬的施工采用逆作法, 分层开挖土体, 分层整体现浇钢筋混凝土帽梁和内衬结构。 内衬与土体分层的高度均控制在3m 以内,共分 8 层, 其中帽梁1 层(宽 3m, 高 3m), 内衬7 层; 第1 层内衬高3m, 宽1.5m; 第2 层 ~ 第5层内衬高 3m, 宽 2m; 第 6 层、 第 7 层内衬高2.1m, 宽2m。

图2 虎门二桥地下连续墙槽段划分Fig.2 Diagram of section division of diaphragm wall of Second Humen Bridge
1.3 施工监测及监测点布置
为研究地下连续墙在开挖过程中的受力与变形, 对其径向位移、 竖向应力及墙外土压力进行监测, 各测点布置如图3 所示。 地下连续墙径向位移采用预埋测斜管进行监测, 测斜管安放于相应槽段的钢筋笼上并在浇筑地下连续墙时随钢筋笼一起下放至槽孔内, 共设置8 根测斜管, 编号为CX01 -CX08; 地下连续墙中钢筋应力采用钢筋应力计进行监测, 钢筋应力计设在槽段中部径向剖面的内弧和外弧主筋上, 每个槽段上监测点沿地下连续墙的深度分为7 层布置(4.5m ~22.5m,间隔为3m), 编号为 G01 -A/B ~ G08 -A/B; 墙外土压力的监测通过预埋的土压力计, 在地下连续墙背坑面的监测点分层埋设, 编号为T01-T04。

图3 西锚碇开挖施工测点布置Fig.3 Monitoring points of the west anchorage foundation
2 有限元模型的建立及参数设置
采用通用程序有限元软件ABAQUS 建模, 对地下连续墙锚碇结构的开挖过程进行模拟, 土体、 地下连续墙、 内衬的有限元网格模型分别见图4, 锚碇各部分结构的参数见表2。

图4 有限元网格模型Fig.4 Typical finite element mesh
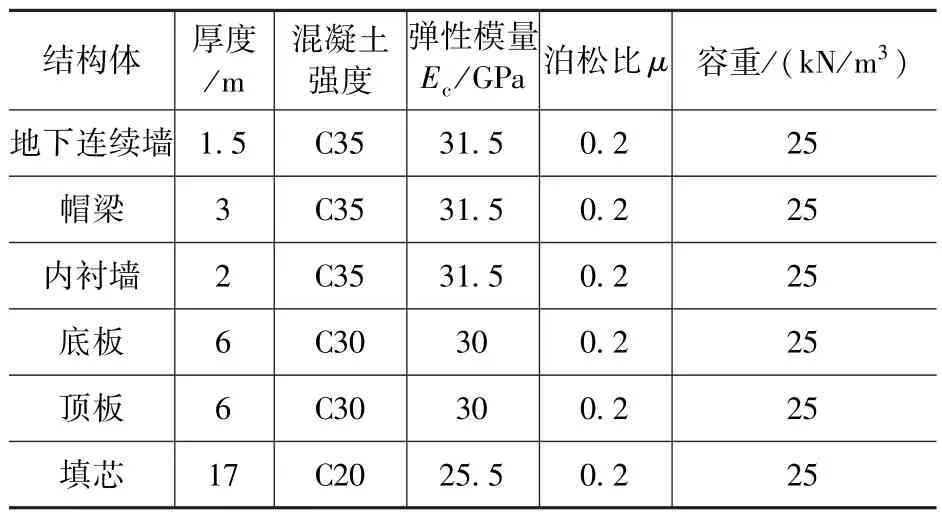
表2 锚碇各部分结构的模型参数Tab.2 Model parameters of anchorage structure for each part
模拟开挖时, 将土体开挖及内衬施工的过程进行分步计算, 通过单元的“生死”功能模拟土体的开挖和内衬的施工; 土层近似等效成厚度相等的成层土, 采用Mohr-Coulomb 弹塑性模型。
地下连续墙和各层土间的接触采用以库仑摩擦模型为基础的面-面接触方式来模拟, 模型中假定地下连续墙的墙背极其粗糙且与填土不相互滑动, 因而墙土界面的外摩擦角α一般为土体内摩擦角φ的 0.67 ~1.00 倍, 模拟中取 0.8 倍,则墙外编号①~④土层的墙土摩擦系数分别为0.07、 0.34、 0.29、 0.47。
3 开挖过程中监测及数值模拟结果分析
3.1 径向位移的实测值与模拟值对比分析
通过将数值模拟结果与47#槽段上CX07 号测斜管的径向位移监测数据进行对比分析, 验证模型的可靠性。
图5 分别为现场监测和数值模拟得到的不同开挖深度d时, 不同埋深h处径向位移s的变化曲线, 其变形规律基本一致。 墙体底部的s随d的增大变化较小, 基本为0; 墙体径向位移最大值smax的位置随d的增大而变化。 开挖初期(d小于 9m),smax一般位于顶部; 随着开挖深度的加大(d=9m ~15m),smax的位置下移至开挖面附近; 当继续开挖,smax的位置位于开挖面以上, 且随着d的加大,smax的埋深位置距开挖面的距离也增大, 最终稳定在埋深h约13m 处。最终的smax约为15mm, 相当于 0.451%H(H为地下连续墙高度), 低于工程中报警值0.6%。
开挖初期, 帽梁的环向约束作用较小, 地下连续墙的位移特征与悬臂梁近似; 之后随着开挖的进行, 顶部的帽梁和底部嵌入的岩层分别在圆形地下连续墙的顶部与底部形成环形约束, 控制住了墙体顶部与底部的位移, 使得围护结构的径向位移最终呈现为“中间大, 顶部较小,底部最小”的形式。 同时由于圆形地下连续墙和内衬的共同作用体现了明显的拱效应, 墙外土压力很大一部分被地下连续墙及内衬的环向压应力平衡, 减小了水平截面上的弯矩, 从而控制住了墙体的径向位移。
3.2 竖向应变的实测值与模拟值对比分析
在实际工程中, 通过对地下连续墙钢筋的应力进行监测并记录, 基于共同变形的原则, 将钢筋应力转换成应变, 从而方便模拟值和实测值进行对比。 将53#槽段 G08 -A 测点的监测数据与模拟值进行对比分析。
图6 分别为现场监测和数值模拟得到的不同开挖深度d时, 地下连续墙竖向应变值ε随墙体埋深h的变化曲线, 两者基本一致。 随着开挖的进行, 同一埋深h处,ε基本上持续增大。 同一开挖工况下,ε先随h的增加呈现递增的趋势, 并在基坑底部附近(埋深约 20m 处)ε达到最大值εmax;之后随着h的增加, 直至岩土分层界面附近,ε持续减小; 然后, 在开挖底部以下嵌岩段, 随着h的增加,ε继续增大。
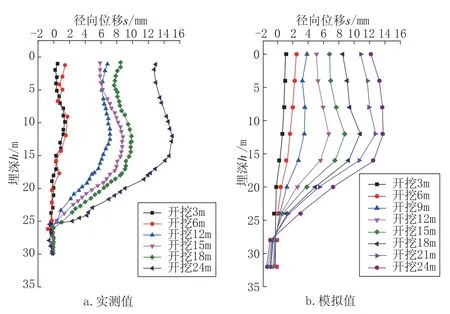
图5 径向位移-埋深变化曲线Fig.5 Relation curves of lateral displacement and burial depth
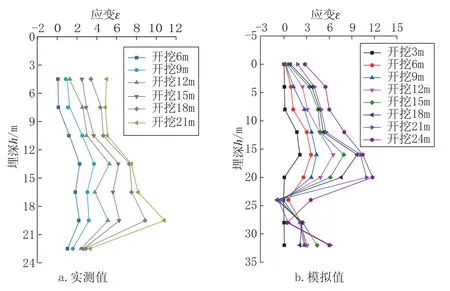
图6 应变-埋深变化曲线Fig.6 Relation curves of vertical strain and burial depth
这是因为随着墙内土体的开挖, 墙内土体对墙体的支撑作用逐步减少, 墙外土压力持续增加, 因而在同一开挖工况下, 随着埋深h的增大, 地下连续墙竖向应变与径向位移的变化相对应。
3.3 墙外土压力实测值与模拟值对比分析
将17#槽段T02 墙外土压力监测点的数据与模拟值结果进行对比分析。 图7 分别为现场监测和数值模拟得到的不同开挖深度d时, 地下连续墙外土压力p随着墙体埋深h的变化曲线, 其变化趋势基本一致。 随着开挖的进行, 墙体的径向位移s增大, 使得同一埋深h处的p持续增大。 同一开挖工况下, 随着h的增加,p在土层中呈现出逐渐递增的趋势,约在h为20m 处,p达到最大值; 之后随着埋深h的增加, 直至岩土分层界面附近(约23m 处),p持续减小; 而在开挖底部以下的嵌岩段, 压力值依旧在逐步增加。
由于作用在墙体外侧的土压力受墙体位移的影响, 当开挖引起墙体产生径向位移, 墙外岩土分界面以上的土压力由静止土压力逐渐转变为主动土压力, 但始终小于理论计算的主动土压力值。 原因是基于极限平衡理论按水土分算方法得到的极限状态下郎肯主动土压力值往往高估了孔隙水压力的贡献, 因而主动土压力的计算值往往偏大。 随着土层过渡到嵌岩段, 岩层对墙体向外径向位移的约束, 导致墙外土压力逐渐转变为被动土压力。 接近土层部分的墙体位移较小, 相应的压力曲线出现下降段, 其后随着h的增加, 墙体向外径向位移增大, 相应的土压力持续增大,甚至超过了土层中压力的最大值。
4 结论
1.墙顶的帽梁和底部嵌入的岩层可形成环形约束, 控制住顶部与底部的位移, 随着开挖的进行, 地下连续墙的径向位移逐渐呈现为“中间大, 顶部较小, 底部最小”。

图7 墙外土压力-埋深变化曲线Fig.7 Relation curves of earth pressure and burial depth
2.开挖过程中, 内衬对地下连续墙竖向钢筋应力影响较大, 它与地下连续墙共同受力限制了墙体的竖向应变, 有效地避免了墙体在开挖过程中发生破坏。
3.墙外土压力p随埋深h的增加, 呈现R状分布, 先增加后减小然后再增加。 土层中, 随h的增加, 径向位移s增大, 墙外的土压力逐渐接近理论计算的主动土压力值; 而随着土层过渡到嵌岩段, 岩层对墙体向外径向位移的约束, 导致墙外土压力随埋深h的增加逐渐转变为被动土压力。

