输电线路角钢塔交叉斜材极限承载力研究*

刘洪义 李正良 刘凯

(1.东北电力设计院有限公司 130021；2.重庆大学土木工程学院 400045；3.山地城镇建设与新技术教育部重点实验室(重庆大学） 400045）

引言

随着国内电网工程建设量加大， 在保证电力建设安全性的前提下， 对其经济性提出更高的要求。 等边角钢输电铁塔是目前国内应用最为广泛的架空输电结构， 而交叉斜材是角钢塔的基本支承构件， 约占单基塔重的30%， 研究交叉斜材的受力特性对输电塔的优化设计有重要意义。

目前国内外对交叉斜材的研究内容较少， 尤其是试验研究部分， 缺乏足够的试验数据作为理论研究支撑。 国外学者Donald D.Cannon[1]等进行了两种节间的交叉斜材承载力试验研究， 斜材包括等边角钢和不等边角钢， 指出交叉斜材稳定承载力特点并给出斜材压杆计算长度取值的建议。 Kemp A.R.[2]等改变交叉斜材试验中端部连接的螺栓数量， 以及主材的倾斜角度， 将试验值和美国规范进行对比， 提出更为精确的斜材设计公式。 国内学者朱永庆[3]对 ASCE 手册52 的相关结论以及TLMRC 试验结果进行了分析， 依据所建模型利用微分方程推导出斜材稳定承载力计算公式， 并进一步提出[4]受拉杆件内力变化对受压杆件计算长度的影响作用。 李宏男[5]等利用ANSYS 对交叉斜材极限承载力进行了非线性分析， 提出当拉杆和压杆内力比值在0 到1 变化时， 极限承载力与该比值近似成线性递增关系，并根据分析结果提出一种简单实用的计算方法。陈绍蕃[6]在考虑屈曲相关性的塔架交叉斜材稳定承载力研究中， 主要改变交叉斜材的连接位置，依据弹性稳定理论， 推导出精度较规范高的承载力计算公式。 江文强[7]等利用ANSYS 壳单元建立4 种斜材布置方式的有限元模型， 考虑节点板厚度的影响， 进行非线性分析得到极限承载力，通过对比发现斜材布置方式对极限承载力影响较大， 采用现行规范计算会偏于保守。

本文在上述研究基础上， 根据交叉斜材的受力特点设计全新试验装置， 并扩大试验中交叉斜材拉压比的范围， 对两种常用节间进行了极限承载力研究， 结合ANSYS 有限元分析结果， 给出交叉斜材的受力变化特点。

1 试验概况

1.1 节间设计

1.仅斜材节间

斜材的长度根据试验方案中给定的名义长细比确定， 为研究有辅助材和没有辅助材节间破坏模式的差异， 将两种节间的名义长细比均设为110， 仅斜材节间由斜材最小轴回转半径确定交叉点到斜材端部的较长段。 交叉斜材夹角选择铁塔设计中常用的74°， 斜材短段与长段的比值设定为常用的0.88， 根据低合金高强度结构钢[8]的最新要求， 斜材采用 Q355 钢。 斜材尺寸为L80 ×7， 长度为 3270mm， 连接处螺栓为高强承压型螺栓， 节间具体构造如图1 所示。

图1 仅斜材节间构造(单位： mm)Fig.1 Structure of only diagonal material section(unit: mm）

2.复杂节间

与仅斜材节间不同， 有辅助材的节间斜材长度根据斜材的平行轴回转半径确定， 交叉斜材夹角仍取74°， 短段与长段比值仍为0.88。 辅助材也采 用 Q355 钢， 斜 材 尺寸 不 变， 长 度为5091mm， 辅助材尺寸为 L40 × 4。 图 2 为复杂节间构造。

图2 复杂节间构造(单位： mm)Fig.2 Structure of complex section(unit: mm）

1.2 试验方案

1.加载方案

加载部位由反力框架、 千斤顶、 力传感器、连接件和斜材单肢依次连接， 该反力框架由四根箱型截面钢梁组成， 具有足够的刚度抵抗节间的变形。 一共设置两个千斤顶沿着斜材轴向加载， 由力传感器读取荷载数值， 通过静态应变测试系统可以直接获取斜材端部荷载大小，从而控制加载拉压比。 制作双角钢构件固定千斤顶位置， 保证加载方向始终沿轴向， 复杂节间的辅助材端部利用连接件与反力框架相连，实现对辅助材的端部约束。 节间底部利用厚20mm 的钢板支座与框架螺栓连接固定。 图3 为两种节间的加载装置。

图3 加载装置Fig.3 Test set-up

试验开始前通过预加载判断各项测试指标变化在合理范围内， 然后开始正式加载， 加载制度为单调静力分级加载制度， 加载过程中通过油泵控制拉压比保持稳定， 直到斜材发生失稳破坏。

2.测点布置方案

除了在节间斜材端部布置力传感器来获取极限承载力外， 还需要在试验中测量关键截面的平面外位移和应变。 截面的平面外位移使用拉线式位移传感器进行测量， 仅斜材节间和复杂节间均测量7 个方向的位移， 包括2 个沿斜材轴向的位移， 另外5 个位移布置在交叉点， 以及交叉点与斜材端部之间的中间位置截面。 仅斜材节间的应变片布置在交叉点处以及交叉点与斜材端部之间的中间截面处。 复杂节间应变片布置在各螺栓连接处之间的中间截面以及辅助材跨中截面。 以上各截面为两种节间的平面外位移和应变控制截面。

3.加载工况

根据《架空输电线路杆塔结构设计技术规定》[9]中的内容， 交叉斜材计算长度的取值方法以拉压比为-0.2 作为分界点， 因此试验工况以拉力等于压杆压力的20%分级展开， 这里规定将一拉一压时的受压杆和同时受压时压力较大的杆统称为压杆。 输电塔在实际建造中设计使用更多的是复杂节间， 在有限的试验资源下应重点分析复杂节间的试验现象， 因此扩大复杂节间的拉压比范围从-1.0 到1.0， 并且在扩大的基础上减小拉压比增量， 以此获得复杂节间更为精确且全面的试验数据。 为防止试验偶然误差， 每种拉压比进行3 次对比试验。 本文涉及的试验工况见表1。

表1 节间试验工况Tab.1 Test conditions of sections

2 试验结果及分析

2.1 仅斜材节间试验结果

试验结果表明， 仅斜材节间的破坏模式均为压杆长段发生屈曲破坏， 图4 列举了拉压比分别为0.2 和-0.6 的结构失效图， 当拉压比小于或等于-0.2 时， 压杆长段绕最小轴发生失稳。 当拉压比大于-0.2 时， 压杆长段绕平行轴失稳。

图4 仅斜材节间失稳破坏Fig.4 Deformation of the only diagonal material section

图5 提取了交叉点的荷载平面外位移曲线以及压杆加载点的荷载轴向位移曲线， 位移均取绝对值。 由荷载位移曲线可以看出， 在达到峰值荷载前， 交叉点的荷载-平面外位移曲线变化趋势相近， 说明仅斜材节间在不同拉压比下达到极限承载力前拥有相似的受力状态， 相同荷载下， 一拉一压状态的交叉点位移要大于同时受压状态。过了峰值荷载后， 交叉点的刚度随拉压比增大而减小， 因为拉杆的支撑作用增大了交叉点的刚度。

对于荷载- 轴向位移曲线， 随着拉压比增大， 拉杆对压杆在交叉点的约束逐渐减弱， 压杆的轴向位移峰值逐渐减小。 不同拉压比情况下其曲线变化基本类似， 表明仅斜材节间的破坏模式与两斜材的拉压比关系不大。 随着持续加载， 拉杆不同的受力情况会对压杆刚度产生不同的影响， 拉杆受压时压杆的轴向刚度比拉杆受拉时大。

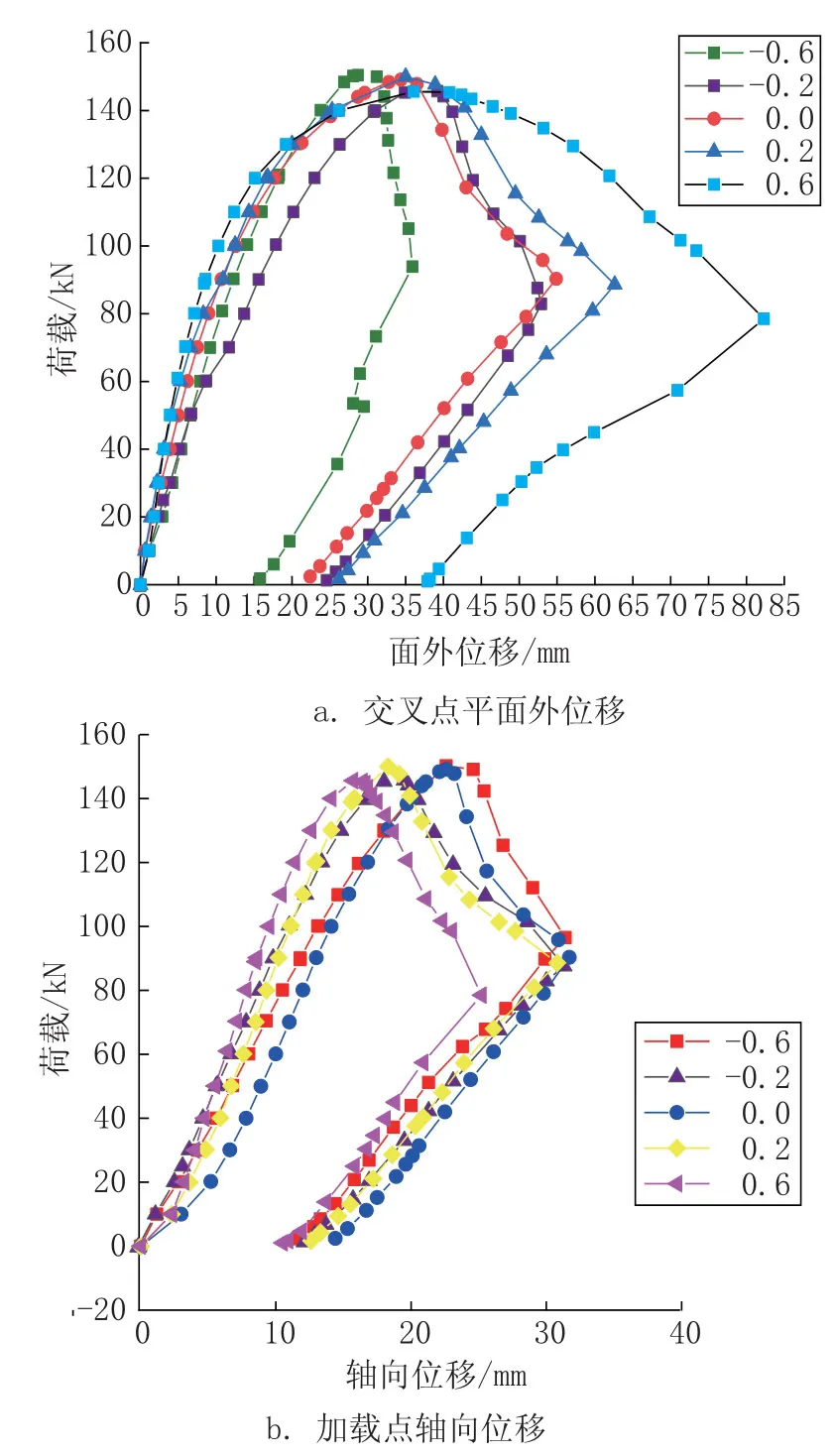
图5 仅斜材节间荷载-位移曲线Fig.5 Load-displacement curves of only diagonal material section

分析应变数据， 当结构最终破坏时， 最大应变截面位置不受拉压比影响， 均在压杆长段中点附近， 与节间最后的破坏模式相符合。 对于压杆， 在到达极限承载力之前， 压杆交叉点与端部之间的中间部分应变增长速度要快于交点处应变增长速度， 到达极限荷载后， 压杆三个控制截面应变较为接近。

当拉压比≤-0.2， 到达极限荷载时， 压杆控制截面的应变要小于拉压比＞-0.2 时的应变，这表明当拉杆拉力不大或拉杆受压时， 压杆受到轴向压力会带动节间向平面外变形， 从而带动拉杆也向平面外变形， 在拉杆加载端产生支反力，使拉力读数增大， 为了保证拉压比， 采取放松拉杆加载端或者使拉杆由受拉转变为受压， 这样使平面外约束减弱， 加速了节间平面外变形， 应变读数也随之增大。

拉杆的三个控制截面最大应变在交叉点处，并且随着拉压比增大， 拉杆的约束效果减弱， 节间平面外变形加大， 拉杆交叉点处的应变也随之增大。

2.2 复杂节间试验结果

与仅斜材节间不同， 复杂节间的破坏模式存在压杆长段屈曲和压杆整体屈曲两种情况。 图6列举了拉压比分别为0.8 和-0.2 的结构失效图。当拉压比≤-0.2 即两根杆为一拉一压且拉杆内力大于或等于压杆的20%时， 复杂节间发生破坏的位置从压杆长段中间开始， 当拉压比大于-0.2， 则压杆带动整个节间发生整体平面外屈曲。 复杂节间均绕平行轴发生屈曲， 可见辅助材增强了交叉斜材的整体稳定性。 如图6 所示， 压杆绕其平行轴失稳， 可以看到半波形失稳模式且拉压比越小这个半波的趋势越明显， 这与目前的理论研究比较吻合。

图6 复杂节间失稳破坏Fig.6 Deformation of the complex section

图7 提取了复杂节间交叉点的荷载-平面外位移曲线和压杆加载点的荷载-轴向位移曲线，位移取绝对值。 分析表明， 交叉点平面外位移在荷载较小时， 不同拉压比对曲线变化影响较小，随着荷载增大， 越接近极限承载力， 拉压比对曲线变化影响越明显。 拉压比越大即另一杆提供的支撑越小， 交叉点的面外刚度就越小， 且变化幅度远大于仅斜材节间。

对于荷载-轴向位移曲线， 与仅斜材节间区别明显， 另一杆受拉即拉压比为-1.0、 -0.6、-0.2 时的曲线相似度较大， 可以看出拉杆内力的大小对结构的稳定承载力影响较小。 随着拉压比增大， 拉杆对压杆在交叉点的约束逐渐减弱，压杆的轴向位移峰值逐渐减小。 荷载较小时各拉压比下的压杆刚度相差不大。 随着荷载增大， 另一杆受压节间的刚度反而增大， 该趋势比仅斜材节间的更为明显。

图7 复杂节间荷载-位移曲线Fig.7 Load-displacement curves of the complex section

分析控制截面的应变， 由于节间半波失稳模式与拉压比有关， 当拉压比≥0.8 时， 此时半波失稳模式较不明显， 节间整体向外发生平面外屈曲， 控制截面应变分布较为均匀。 当拉压比≤0.5 时， 随着拉压比减小， 半波失稳模式越明显， 斜材交点和压杆加载端之间的部分斜材屈曲明显， 导致与其相连的左边长辅助材发生明显变形， 左边长辅助材的应变明显高于其他控制截面， 这一现象与复杂节间的破坏模式相吻合。 表2 统计出两种节间的破坏模式随着拉压比的变化。

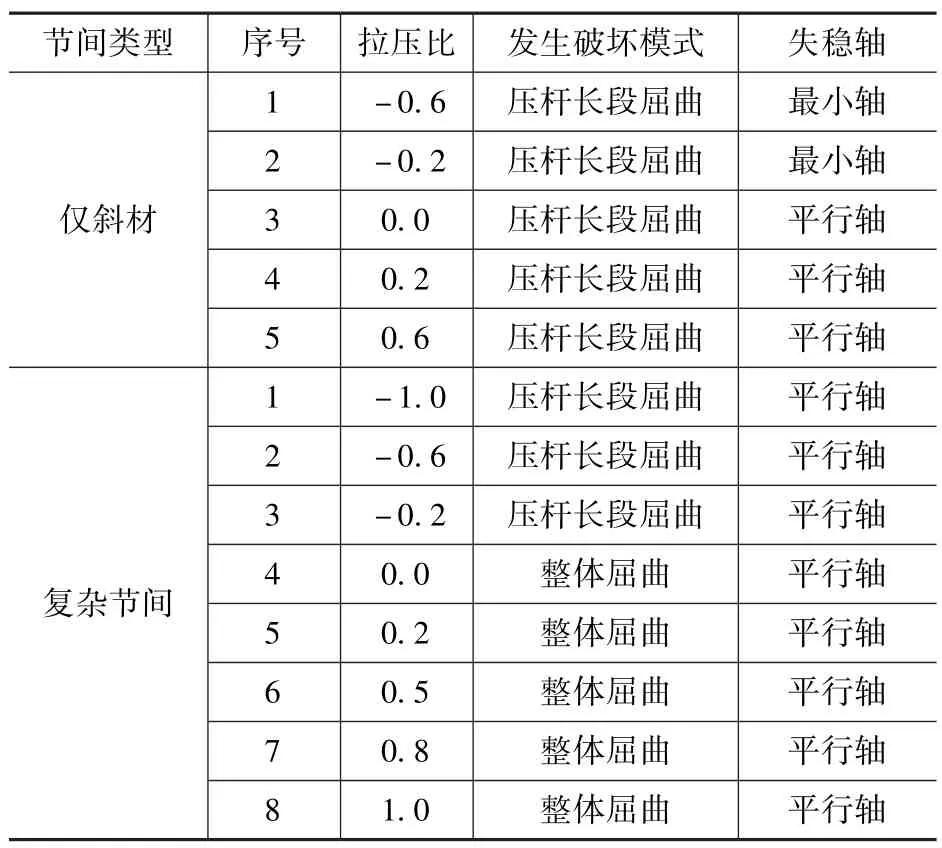
表2 交叉斜材试验破坏结果Tab.2 Test failure results of the cross bracing

2.3 极限承载力

不同拉压比工况下的试验极限承载力均取各自3 组试验的平均值。 从图8 可以看出， 仅斜材的极限承载力随着拉压状态的改变浮动并不大，仅斜材节间拉压比为-0.6 时的极限承载力为152.53kN， 拉压比为 0.6 时极限承载力为143.88kN， 相差了5.67%左右， 而拉压比为0.2时的承载力却高于拉压比为-0.2 时， 未表现出承载力随拉压比增大而严格减小的规律， 这是由于仅斜材节间的整体性较弱， 破坏荷载只跟压杆长段的失稳相关， 另外一杆的受力状态对压杆的影响不大。

图8 不同拉压比的极限承载力Fig.8 The ultimate bearing load of the different T/C ratio

对于复杂节间， 其极限承载力受拉压比影响较大， 拉压比为-1.0 时与拉压比为1.0 时相比， 极限承载力改变了47.66%。 随着拉杆由受拉转变为受压状态， 压杆的极限承载力逐渐减小。 在一拉一压状态下， 拉杆拉力的变化对压杆承载力影响较小， 拉压比从-1.0 到-0.2， 压杆承载力变化了4.13%； 而在同时受压状态下， 另一杆压力增大对极限承载力变化影响明显， 拉压比从0.2 到1.0， 承载力变化了33.87%， 但在拉压比到达0.8 后变化减缓， 0.8 到1.0 承载力变化了7.36%。 因为仅斜材节间构件长度由最小轴计算得到， 长度较复杂节间小， 所以仅斜材节间极限承载力总体上大于复杂节间。

3 有限元分析

3.1 有限元模型建立

两种节间整体有限元模型如图9 所示。 根据本文试验构件的力学特点， 选择SHELL181 壳单元进行分析。 该单元有4 个节点， 每个节点包含6 个自由度。 屈服强度和弹性模量设置为材性试验实测值， 钢材密度取下料真实值， 泊松比取0.3， 选择双线性随动强化(BKIN）作为本构模型， 根据材性试验的应力-应变曲线， 切线模量设置为弹性模量的1%。 试验中底座未发生变形，在有限元分析中将其弹性模量放大100 倍， 以此保证构件破坏而底座不发生变形， 同时减少应力集中， 有利于计算收敛。

图9 有限元节间模型Fig.9 Finite element model

本文对螺栓连接处网格进行细化， 图10 展示了交叉斜材连接处的网格细化方式。 网格划分方式为自由划分， 自由划分网格的基本尺寸为20mm。

图10 网格细化示意Fig.10 Meshing subdivision diagram

根据试验加载工况， 在斜材上部螺孔周围施加沿斜材方向的节点集中荷载来模拟试验工况，同时约束加载点在其余两个方向的位移， 保证加载方向始终在斜材轴向。 支座底部为固定端， 约束支座底面所有节点的自由度。 因构件连接处的螺孔连接紧密， 有限元分析中将交叉斜材连接处和支座连接处等周围部分节点进行耦合， 以简化计算模型， 对比采用SOLID186 实体单元在螺孔处建立的螺栓模型， 两者分析结果接近， 表明该简化方式可行。

3.2 有限元分析结果

1.破坏模式对比

两种节间在有限元分析结果中的破坏模式和试验结果相符合， 为节省篇幅， 图11 给出了仅斜材节间拉压比为-0.6 和复杂节间拉压比为0.8 两种工况的破坏形态。 两种节间屈曲时平面外位移最明显， 因此选择平面外位移作为图11 中的量值。 仅斜材节间拉压比为-0.6 发生压杆长段屈曲，且沿着最小轴失稳； 复杂节间拉压比为0.8 发生压杆整体屈曲， 沿着平行轴失稳。 与试验现象吻合。

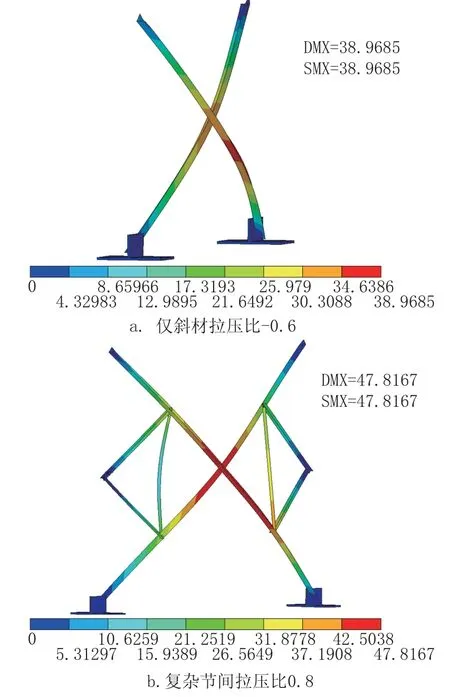
图11 破坏形态(单位： mm)Fig.11 Failure mode(unit: mm）

2.荷载-位移曲线对比

图12 为两种节间的交叉点荷载-面外位移曲线试验结果和有限元结果的对比。 因复杂节间工况较多， 此处省略拉压比为1.0 时的对比， 拉压比为1.0 的有限元分析结果和拉压比0.8 类似。 观察发现， 随着拉压比增大， 极限承载力减小， 曲线整体变化趋势与试验所得曲线一致。 构件刚度随着拉压比的变化趋势也与试验结果相同。 进入非线性段后， 部分工况有限元计算收敛困难， 因此缺少明显的下降段。 试验中存在缝隙等误差， 以及各构件连接处不是完全耦合， 底座也不是完全固接， 综合以上原因， 部分工况在峰值荷载时的位移误差较大， 仅斜材节间峰值荷载位移与试验结果吻合得更好， 复杂节间构件尺寸更长， 误差相对较大。 有限元分析结果中的轴向位移总体较小， 但整体变化趋势与试验结果相吻合。

3.有限元应变分析

观察有限元中的应变分布可以发现， 应变分布规律与试验结果较为吻合， 仅斜材节间压杆长段和交叉点附近应变较大， 拉杆最大应变在交叉点处； 复杂节间的半波失稳使左侧长辅助材应变明显增大， 应变变化趋势也与试验结果较为吻合。 为节省篇幅， 图13 给出了仅斜材拉压比为-0.2 和复杂节间拉压比为0.2 时， 荷载为峰值荷载的应变分布。

图12 荷载-位移曲线对比结果Fig.12 Comparison results of load-displacement curves

图13 应变分布Fig.13 Strain distribution

3.3 极限承载力对比分析

图14 不同拉压比极限承载力对比Fig.14 Comparison of ultimate bearing capacity at different tension-compression ratios

图14 为不同拉压比下两种节间的极限承载力试验值与有限元值的对比曲线， 分析 表 明，有限元计算的极限承载力随拉压比的变化趋势与试验结果相符合。 因试验中存在螺栓孔隙以及试件安装误差， 轴向加载也存在一定偏差， 所以有限元值与试验值有一定出入， 但整体与试验值吻合良好， 表明本文的有限元分析模型具有合理性。

表3 为两种节间极限承载力的试验结果、 规范[9]计算结果以及有限元计算结果的对比。 分析表明， 试验值与规范值和有限元值计算结果吻合较好， 整体随着拉压比的变化趋势一致。 试验极限承载力在多数拉压比工况下大于规范计算结果， 表明规范计算有较多的富余。

表3 试验承载力与规范承载力、 有限元结果对比Tab.3 Comparison of test results， code results and finite element results

仅斜材节间试验承载力与规范计算承载力比值最大为1.19， 最小为1.04； 复杂节间试验承载力与规范计算承载力比值最大为1.19， 最小为1.00。

4 结论

本文对两种节间在不同拉压比下的稳定承载力进行试验研究， 同时建立等比例ANSYS 有限元模型进行数值分析， 主要得出以下结论:

1.仅斜材节间在不同拉压比下破坏模式均为压杆的长段发生屈曲， 屈服区域位于压杆长段中点和交叉点之间， 当拉压比≤-0.2 时， 绕截面最小轴失稳， 当拉压比＞-0.2 时， 绕截面平行轴失稳。

2.复杂节间存在压杆长段屈曲和压杆整体屈曲两种破坏模式， 当拉压比≤-0.2 时， 复杂节间压杆长段发生屈曲破坏， 当拉压比＞-0.2 时，发生压杆整体平面外屈曲破坏。 压杆呈半波形失稳且拉压比越小半波的趋势越明显， 复杂节间的屈曲破坏均绕平行轴产生。

3.随着拉压比增大， 拉杆对压杆的支撑作用减弱， 压杆半波趋势减弱， 仅斜材节间在相同荷载下， 交叉点的平面外位移增大， 压杆的轴向位移减小。 复杂节间拉杆存在同样明显的约束作用，随着拉压比增大， 拉杆支撑作用减弱会使得压杆轴向位移减小， 交叉点平面外位移增大。

4.仅斜材节间在破坏时， 压杆长段中点附近截面应变最大， 随着拉压比增大， 压杆整体的截面应变增大， 压杆交叉点处截面应变最大。 随着拉压比增大， 复杂节间半波失稳模式越明显， 导致与压杆相连的左边长辅助材发生明显变形， 左边长辅助材的应变明显高于其他控制截面。

5.两种节间的极限承载力均随拉压比增大而减小， 复杂节间减小的幅度要明显高于仅斜材节间， 拉压比对仅斜材节间承载力影响较小， 对一拉一压下的复杂节间承载力影响较小， 对同时受压时的复杂节间承载力影响较大。 试验承载力在多数拉压比工况下要高于规范[9]计算结果。