永磁同步电机模糊滑模调速系统设计及优化

许 轲

(华南理工大学机械与汽车工程学院，广东 广州 510641)

永磁同步电机在体积、质量和效率等方面相较其他电机具有较大优势，因此在工业领域应用广泛。对永磁同步电机转速控制的研究是学术界的热点，在传统比例-微分(proportion integration，PI)控制的基础上，相关学者提出了滑模控制、自适应控制、神经网络控制等提高调速过程快速性和稳定性的方法，但实际工程应用中，仍以PI控制和滑模控制为主。

滑模控制具有开关特性，可使系统在一定条件下沿设计好的状态做小幅、高频率上下运动，该运动对外界扰动与参数改变不敏感，因此滑模控制系统鲁棒性好[1]。为进一步提高滑模控制的响应速度，高为炳院士提出指数趋近律以加快趋近阶段的运动速度，但同时也给滑动模态阶段带来了更大的抖振[2]。为削弱抖振现象，相关学者又提出多种方案，如变指数趋近律滑模[3]、边界层积分滑模[4]以及引入非线性项的末端滑模[5]等，这些方法使得滑模增益减小，在削弱抖振的同时对滑模控制的快速性和鲁棒性又产生了一定的影响。于是多位学者提出将模糊控制与滑模控制相结合[6-7]，柔化控制信号，在降低抖振的同时，减小对滑模控制系统快速性和鲁棒性的影响。

目前永磁同步电机(permanent magnet synchronous motor，PMSM)调速系统中多采用基于指数趋近律的滑模控制方法[8-10]，模糊滑模控制则主要针对指数趋近律中的等速趋近项系数，等速趋近项主要在系统状态接近滑模面时发挥作用，因此通过模糊控制柔化该项系数，可使系统状态点平稳地进入滑模面，进而削弱系统抖振[11]，但需注意的是指数趋近律中的指数趋近项也会影响系统的响应效果。普通模糊滑模控制中，该项系数固定，且为了兼顾大阶跃时的响应效果，该值多取较大值，此时系统状态点能快速到达滑模面，但在抖振时会增大抖振幅度，且在小阶跃时易带来较大超调[12]。因此，本文在模糊化等速趋近项系数的基础上也对指数趋近项系数进行模糊化，设计了同时模糊化等速趋近律系数和指数趋近律系数的模糊滑模控制系统，并应用于PMSM转速控制系统。

1 永磁同步电机建模

在dq坐标系中，永磁同步电机系统可用以下4个方程描述：

1)定子电压方程。

(1)

式中：id，iq分别为两相旋转绕组中的电流；R为绕组电阻；ud和uq分别为两相旋转绕组中的电压；ψd和ψq分别为两相电流产生的磁链；ωe为转子电角速度。

2)定子磁链方程。

(2)

式中：Ld和Lq分别为d轴和q轴电感；ψf为永磁体磁链。

3)电磁转矩方程。

Te=1.5np(ψdiq-ψqid)

(3)

式中：Te为电机电磁转矩；np为电机极对数。

4)运动平衡方程。

(4)

式中：J为整个机械负载系统折算到电机轴端的转动惯量；TL为电机轴端的负载转矩。

2 模糊滑模转速控制系统设计

2.1 滑模控制设计

在转速控制系统中，定义切换函数为：

s=cx1+x2

(5)

式中：c为待设计变量；x1,x2为系统状态变量。x1,x2定义为：

(6)

式中：ωref为电机的目标电角速度。

为求趋近律，先对状态变量求导：

(7)

于是，求得趋近律为：

(8)

为保证滑模面可达，即满足Lyapunov条件，采用指数趋近律形式：

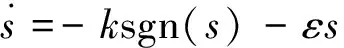
(9)

式中：k为等速趋近项系数，需满足k>0；ε为指数趋近项系数，需满足ε>0。

对比式(8)和式(9)，可求得滑模转速控制系统的控制率为：

(10)

式中：τ为时间变量。

对上述滑模转速控制系统做如下分析：

利用Lyapunov函数来判断系统的稳定性，定义Lyapunov函数V=0.5s2，采用指数趋近律，可得：

(11)

可见，该控制系统是渐进稳定的，解式(11)可得：

(12)

可见，函数V(t)指数收敛，收敛速度取决于ε，当|s|较大时，指数项εs能保证系统状态点以较大速度趋近于滑动模态，因此指数趋近律尤其适合解决具有较大阶跃的响应控制问题，但若ε取值过大，在较小阶跃时又会出现超调量过大的情况，且稳态时会加剧系统抖振。通过模糊控制实时调节ε的取值，可使系统在大阶跃和小阶跃下均具有较好控制效果。

指数趋近中，趋近速度会逐步减小到0，因此单纯的指数趋近，运动点是渐进逼近切换面，不能保证在有限时间内到达切换面，所以需要引入等速趋近项ksgn(s)，当s接近于0时，趋近速度是k，而不是0。k与系统状态点趋近滑模面的速度以及状态点在滑模面上滑动时的抖动幅值相关，因此k的取值将对滑模控制系统稳态性能产生直接影响。本文通过模糊控制实时调整k，在保证系统状态点快速趋近滑模面的同时削弱系统抖振。

2.2 模糊控制设计

模糊滑模转速控制系统结构框图如图1所示。

2.2.1ε值模糊控制设计

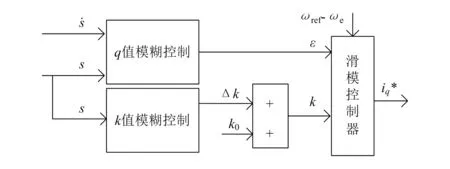
图1 模糊滑模转速控制系统结构框图

图2 ε值模糊控制输入输出隶属度函数

模糊控制规则表见表1。

表1 模糊控制规则表

根据模糊规则得到模糊控制系统的3D效果如图 3所示。在Simulink中采用重心法进行解模糊计算：

(13)

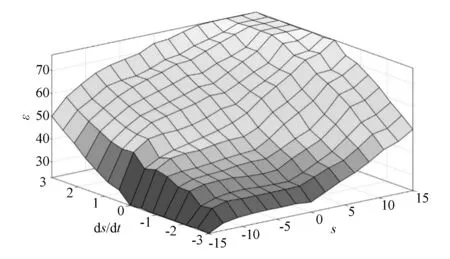
图3 模糊控制系统输入输出3D效果图

2.2.2k值模糊控制设计

k值模糊控制的输入为切换函数s，输出为k的浮动值Δk。同样根据普通滑模控制系统设计及调试时获得的经验，定义s和Δk的论域均为{-3,-1,0,1,3}，输入输出隶属度函数图像如图4所示，同样采用重心法解模糊得到实际Δk值。

图4 Δk值模糊控制输入输出隶属度函数

3 仿真验证

3.1 仿真模型搭建

基于以上分析设计模糊滑模转速控制系统，并在Simulink中搭建基于该控制系统的电压解耦型双闭环矢量控制系统，其结构框图如图5所示。

其中电机参数见表2。

图5 电机控制系统结构框图

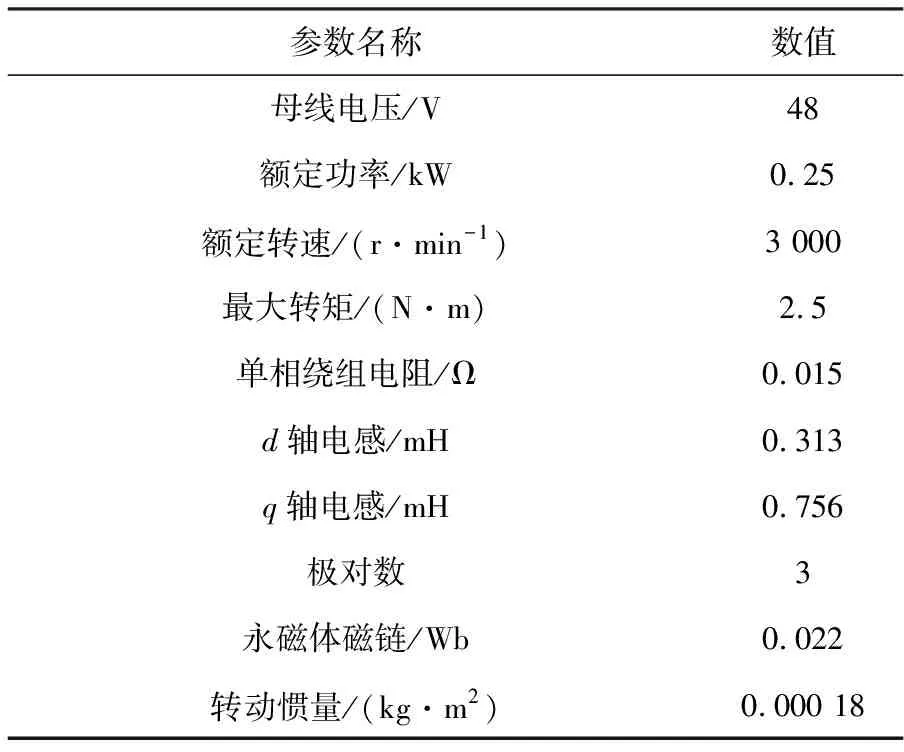
表2 电机参数

3.2 仿真结果及分析

为验证本文所提模糊滑模转速控制系统在全速范围内的有效性，以普通滑模控制以及仅模糊化k值的模糊滑模控制作为对照组，分别给定500 r/min和2 500 r/min为目标转速，同时在0.1 s处将负载转矩由0.5 N·m提升到1.5 N·m，得到3种方法在低转速和高转速下的转速响应曲线，如图6和图7所示。仿真中，普通滑模控制系统中参数取值：c=5.5，k=60，ε=75，模糊滑模控制系统中参数取值：k0=60。定义转速进入2%误差时系统进入稳态，3种方法转速响应效果对比以及抗干扰性对比见表 3、表 4。

由表可见，在低转速和高转速下，模糊滑模控制的调速效果和抗干扰性要明显优于普通滑模控制，并且同时模糊化k值和ε值的模糊滑模控制较仅模糊化k值的滑模控制在转速稳定时间、超调量和抗干扰性方面均有所提高。在500 r/min低转速下，同时模糊化k值和ε值的模糊滑模控制转速响应时间缩短30.5%，超调量降低14.3%，负载突变时，转速波动下降31.3%，转速重新稳定时间缩短41.7%。各指标均有较大提升，但2 500 r/min高转速下，稳定时间提升12.7%，超调量和负载突变时转速波动的优化效果不甚明显。

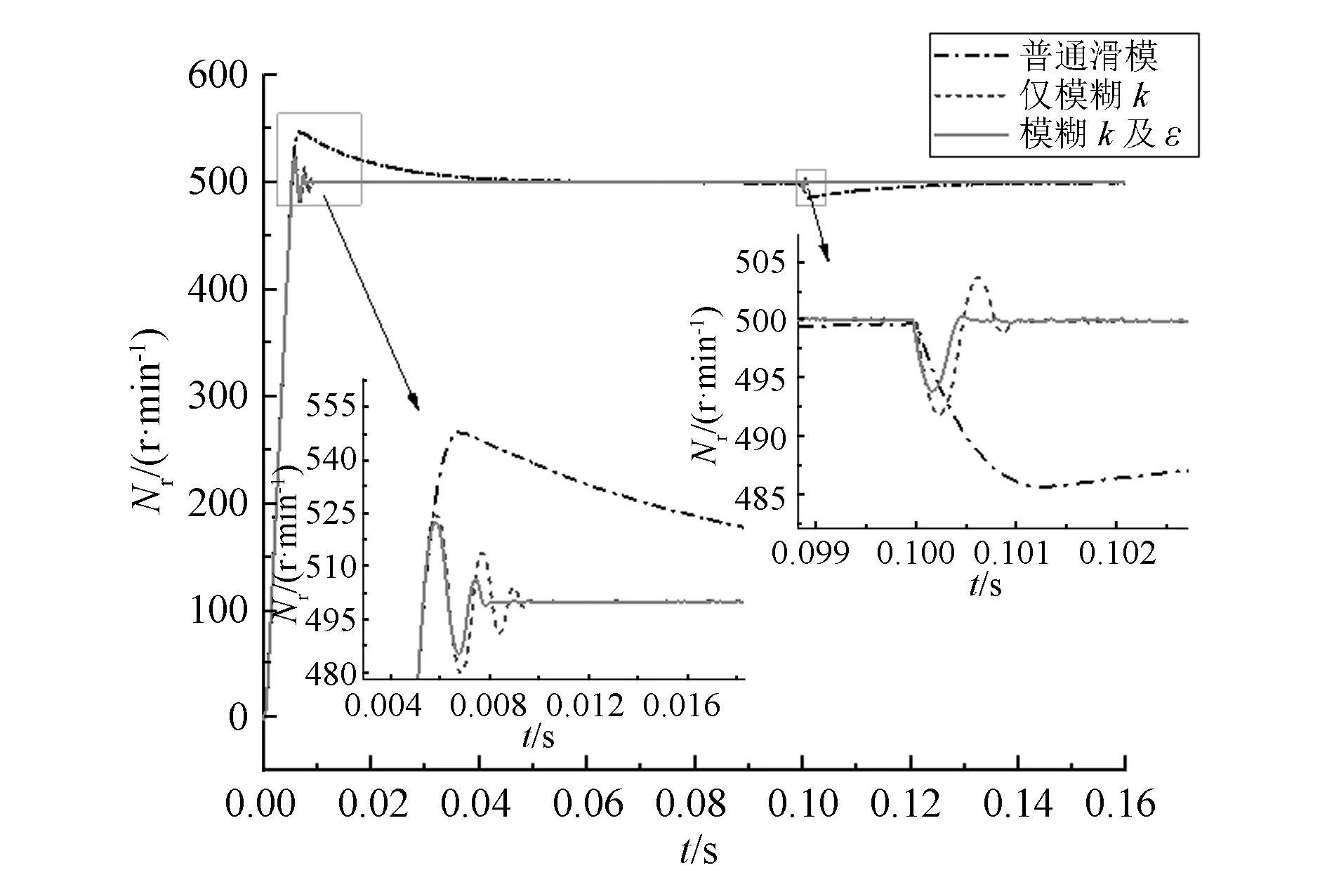
图6 转速为500 r/min时3种方法转速响应曲线

图7 转速为 2 500 r/min时3种方法转速响应曲线

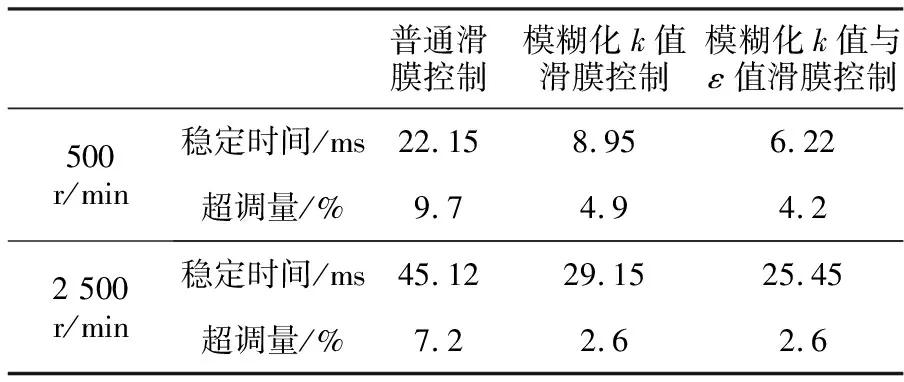
表3 3种方法转速响应效果对比

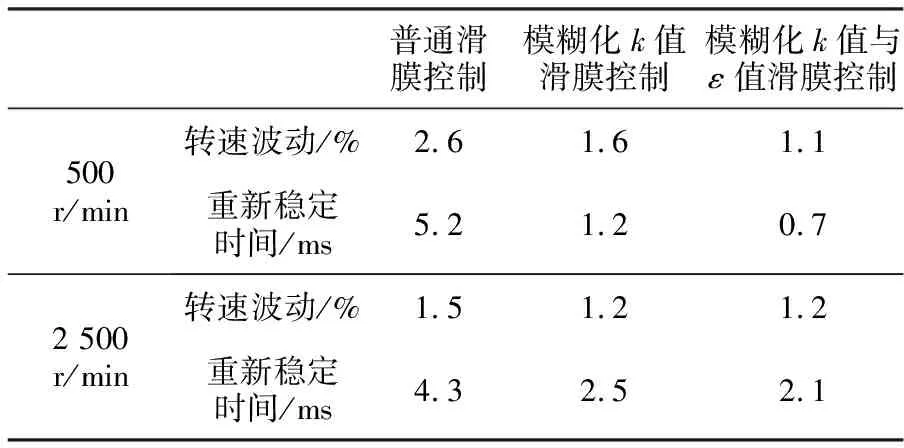
表4 3种方法抗扰性对比

4 结束语

本文基于模糊控制和滑模控制的思想，设计了应用于永磁同步电机调速系统的模糊滑模转速控制系统，在对等速趋近项系数k进行模糊化的基础上，设计了对指数趋近项系数ε进行模糊化的二维模糊控制系统，仿真结果显示，相较于仅对k值进行模糊化的模糊滑模控制，同时模糊化k值和ε值的模糊滑模控制调速效果更好，在稳定时间、超调量和抗干扰性等方面均具有一定的优越性，尤其在低速时，仅模糊化k值的滑模控制需要兼顾目标转速较高时的调速过程，因此在低速阶段响应时间和超调量均会较大，而同时对ε值进行模糊化的方案很好地解决了该问题。