基于指数平滑和XGBoost的航空发动机剩余寿命预测

赖儒杰 范启富

（上海交通大学电子信息与电气工程学院 系统控制与信息处理教育部重点实验室）

航空发动机是飞行器的核心部件， 其稳定、可靠地运行是飞行安全的基础。 传统的发动机维护采取简单的被动和主动策略，即当发动机出现故障时进行零件维修或更换，或者发动机运行到默认时限则对零件统一更新［1］。 由于航空发动机结构复杂， 运行状态受众多环境因素的影响，其使用寿命范围较大，固定的默认时限设置无法权衡维护策略的安全性和经济性。 近年来针对航空发动机的故障预测与健康管理 （Prognostics and Health Management，PHM）的研究广泛开展，通过准确预测剩余寿命 （Remaining Useful Life，RUL），可以对发动机的健康状态即时监测，采取合理措施进行维护，从而在保证飞行器可靠飞行的同时，降低发动机维护成本。

PHM领域的RUL预测方法主要分为3类：基于物理模型、 基于数据驱动和二者结合的方法［2，3］。基于物理模型的方法需要对部件进行退化过程建模，高度依赖部件原理的相关知识；基于数据驱动的方法是利用统计学、机器学习及深度学习等方法对多源传感器的数据进行分析从而得出预测模型；二者结合的方法则在提出物理模型的基础上，用数据驱动方法对模型参数进行学习和调优。

由于航空发动机复杂的结构和工作原理使得准确建模极为困难，对RUL预测采用上述第1类和第3类方法的文献较少， 基于数据驱动的方法则被广泛研究。 传统机器学习方面：文献［3］使用滑动时间窗处理原始信号的时间序列，对时间窗内信号提取平均值和趋势系数作为特征，最后利用支持向量回归（SVR）进行拟合。 该方法的特征处理简单有效，模型参数少，易于调整，但在官方评价指标上预测效果欠佳。 深度学习方面：文献［4，5］分别使用卷积神经网络（CNN）和长短期记忆网络（LSTM）搭建深度模型进行特征提取，后接全连接网络进行回归；文献［6］提出一种基于双边长短期记忆网络（BiLSTM）的自编码器（AE）结构计算健康指数（HI），再对HI进行线性回归；文献［7］则将神经网络与集成学习结合，使用差分进化算法训练出一种以深度信念网络（DBF）为基学习器的集成模型。 深度学习具有强大的非线性拟合能力，但由于其结构复杂，通常需要大量数据才能较好拟合。 文献［6，7］虽然从模型结构和训练方式上进行改进， 但受制于数据样本较小，预测效果提升有限。

由于航空发动机退化过程中传感器变化呈现明显的趋势性，合理的时域方法可以有效提取特征。 另一方面，一些新兴的机器学习方法在小样本数据集上也表现出强大的回归能力，如Chen T Q和Guestrin C于2016年提出XGBoost，该算法的卓越性能在众多数据竞赛中得到广泛认可［8］。 因此，笔者将传统信号处理方法与XGBoost结合：首先根据传感器信号的变化趋势进行特征筛选，使用指数平滑对传感器数据降噪处理，利用时间窗增强特征，最后使用XGBoost进行回归。 笔者选择在NASA C-MAPSS航空发动机仿真数据集上进行试验。

1 指数平滑

指数平滑（Exponential Smoothing，ES）常采用指数加权移动平均（Exponential Weighted Moving Average，EWMA）实现。 EWMA是一种监测过程平均值的统计方法，其一般形式为［9］：

其中，xt为t时刻真实值，yt为t时刻观测值，衰减因子α∈（0，1）（α为定值）。

笔者采用Python数据分析库Pandas中提出的一种修正权重的观测值计算方式，即各项系数为指数函数的一般加权平均：

式（2）适用于有限长序列的观测值计算，且满足t→∞时与式（1）等价。

对于任一给定α，在计算yt时，由于距离当前时刻较远的xt-i权重较小， 对计算的影响可忽略，因此可理解为近端一定范围s内的xt-i起主要作用，即{xt-i|0≤i≤s-1}。 视s为平滑系数，α与s关系如下：

2 XGBoost

XGBoost 是广义梯度提升决策树（Gradient Boosting Decision Tree，GBDT） 的一种高效实现。GBDT以迭代的方式构建多棵CART树，对每一轮的预测残差逐步进行拟合。 XGBoost在GBDT的基础上对目标函数引入L2正则项和二阶导数，并从系统设计的角度对运算性能进行优化［8］。

考虑数据集D={（xi，yi）}有n个样本，每个样本m维特征（|D|=n，xi∈Rm，yi∈R）。 训练得到K棵树的集成模型，其预测结果表示为：

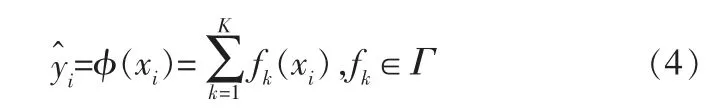
其中，Γ={f（x）=ωq（x）}（q：Rm→T，ω∈RT）为K棵树的集合，q为树的结构，T为树的叶节点个数，ω为叶节点权重。

目标函数定义为：

其中，l为损失函数，Ω为复杂度函数， ‖ω‖2为叶节点权重的L2范数，惩罚系数γ和λ用于调整模型复杂度，控制过拟合。

损失函数可自定义， 但需满足二阶可导，对于回归问题通常采用平方误差：

训练阶段，每一轮增加一棵树对上一轮的预测残差进行拟合，第t轮的目标函数如下：

对损失函数进行二阶泰勒展开，并去除常数项，目标函数改写为：

每一轮迭代采用贪心算法构建CART树，详细过程见文献［8］。

3 数据预处理和特征工程

试验数据来源于NASA C-MAPSS航空发动机仿真数据集中FD001子集。监测数据包括3个操作变量和21个传感器数据。 训练集包含100台发动机从启动到失效各个运行周期的监测数据，最长周期数362cycle，最短周期数128cycle，共20 631个样本； 测试集包含100台发动机从启动到某一运行周期（中断时刻）的监测数据及对应RUL，最长周期数303cycle，最短周期数31cycle，共13 096个样本。

训练集的RUL标签设置通常有两种方式：线性退化和分段线性退化。 考虑运行初期发动机性能较稳定，退化不明显，笔者采用分段模型，初始RUL设置为127cycle［2］，训练集的RUL标签设置如图1所示。

传感器数据变化趋势见表1。 笔者忽略数值恒定的传感器，选取剩余14个传感器的信号作为输入特征［7］。 由于原始信号噪声较大，采用式（2）进行指数平滑处理，使预测算法更好地捕捉信号的趋势变化。 图2展示训练集1号发动机3号传感器信号的平滑效果， 可以看出平滑系数s越大，信号波动越小。

图1 训练集RUL标签设置

表1 传感器数据变化趋势

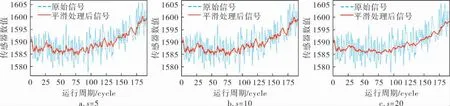
图2 不同平滑系数时的平滑效果

针对多变量时间序列问题，仅使用单个样本点的信息会使得数据利用不充分，因此使用定长时间窗增加各传感器连续时间步历史数据［7］，达到特征增强的目的。 同时由于运行时长也是影响RUL的重要因素之一， 运行时长也被作为一维特征。 设时间窗宽度为Ntw（含当前时刻），选取传感器14个， 则特征工程处理后每个样本点包含14×Ntw+1维特征。 考虑测试集最短周期数为31cycle，本试验中Ntw取值为30。

由于各传感器真实数值差异较大，训练前需对各特征进行归一化处理， 笔者采用Min-Max归一化，将特征值映射到［0，1］范围：

4 试验结果分析

该数据集通常采用Score、RMSE和Accuracy指标对预测结果进行评价［3］（其中Score为该数据集的官方指标）：

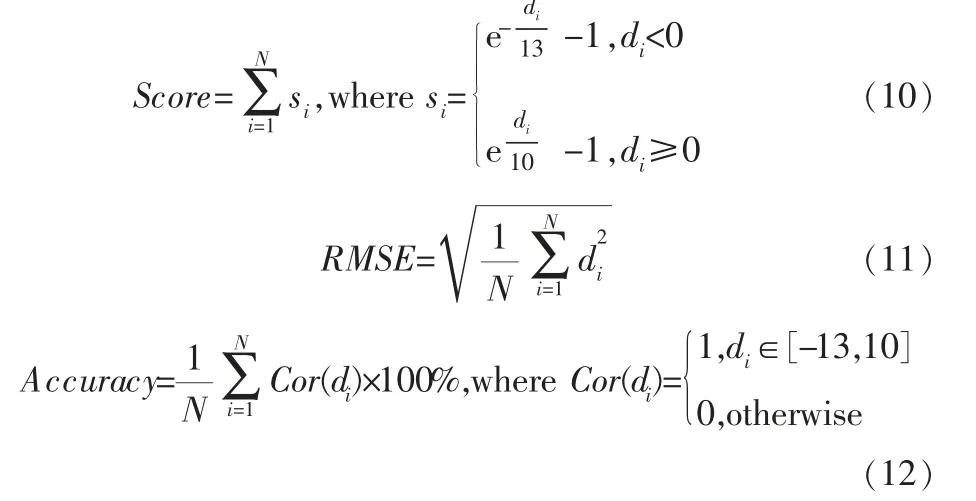
其 中，di为 预 测 误 差，di=RULest，i-RULactual，i，RULest，i和RULactual，i分别为第i个样本的RUL预测值和 真 实 值，Cor（di）表 示 当 预 测 误 差di属 于［-13，10］区间时认为该样本估计准确。

绘制的指标评价结果如图3所示。 Score为非对称指标，对过预测惩罚较大，对欠预测惩罚较小；RMSE为对称指标；Accuracy用于统计在合理误差范围内的预测结果比例。

图3 评价指标结果

试验使用Python 语言下scikit-learn 接口的XGBoost回归模型，在经指数平滑和特征工程处理后的数据集上进行训练和测试， 训练中损失函数使用XGBoost 算法默认的平方误差 （式（6））。对于不同平滑系数处理后的训练集，分别采用5折交叉验证进行超参数选择，得到各条件下的模型最优参数， 然后使用训练集所有数据对最优参数下的模型进行训练， 最后对测试集中断时刻的RUL进行预测， 并结合其真实RUL进行效果评估，试验结果见表2（表中粗体字为该列最佳值）。

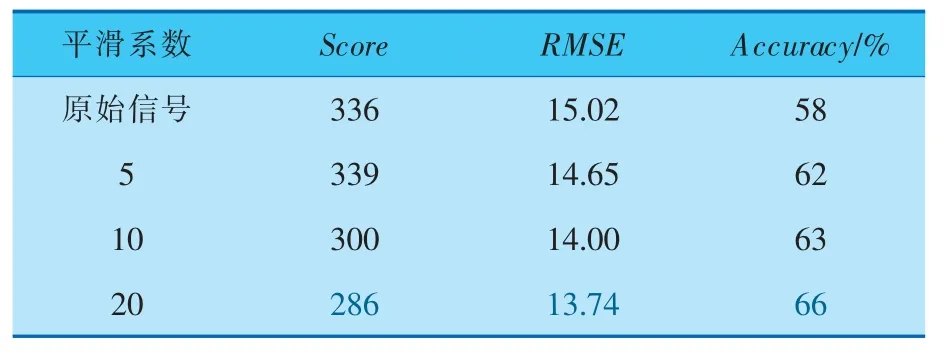
表2 不同平滑系数取值下XGBoost预测效果对比

由表2可知， 随着平滑系数的增大平滑效果增 强，Score 整 体 呈 减 小 趋 势，RMSE 减 小，Accuracy提高，即算法性能在3个指标衡量下均得以提升，由此推测XGBoost算法对噪声较敏感，使用平滑后的数据作为输入，可使算法更好地捕捉趋势特征，取得更好的预测效果。 平滑系数为20时，XGBoost的参数列表和预测结果见表3、图4。

表3 XGBoost参数列表

图4 XGBoost预测结果

进一步将笔者所提方法与其他主流方法的预测效果进行比较分析，结果见表4（表中粗体字为该列最佳值）。 笔者所提方法在RMSE指标上取得最好结果， 考虑XGBoost采用平方误差作为损失函数进行训练， 可认为充分发挥了XGBoost的拟合能力。 对比BiLSTM-ED方法，BiLSTM-ED的Score值更小， 而RMSE略高， 且Accuracy明显较低， 推测该方法倾向于欠预测RUL。 对比SVR方法，SVR的Accuracy略高于笔者所提方法，而Score则明显较高，推测该方法在误差边界外的预测值偏离真实值较大。

表4 笔者方法与其他主流方法预测效果对比

综上所述，笔者所提方法预测值相对于真实值总体偏差最小， 且预测没有明显偏向性；在RMSE指标上取得最优结果，Score和Accuracy指标略差于最好方法，但显著优于其他方法，因此可以认为笔者所提方法综合性能最佳。

5 结束语

针对航空发动机退化过程多源传感器测量信号，使用修正权值的指数平滑方法对有限长时间序列数据进行降噪处理，并添加时间窗内历史数据进行特征增强， 使XGBoost的预测性能得到大幅提升。 通过与其他前沿算法进行对比，可验证笔者所提方法在对称指标上预测效果最佳，在非对称指标上仅次于最优方法，因此可体现出方法优异的综合性能。 下一步工作可研究其他信号处理算法进行数据平滑（如卡尔曼滤波）以及使用非对称损失函数训练XGBoost对其预测性能的影响。