一种面向复杂多用户类型的天然气站场分输优化方法及应用

王树祺 毛炳强 张 麟 吕 峰 颜 辉 贾立东 张 超 殷卫兵

（1.中国石油天然气股份有限公司北京油气调控中心；2.中国石油天然气股份有限公司管道分公司；3.中国石油天然气股份有限公司管道大连输油气分公司；4.北京安稳优自动化技术有限公司）

随着人们环保意识的增强，天然气的使用越来越普及。 但国内的部分天然气分输站场仍存在分输控制质量和效益欠佳的情况。 针对如何将天然气安全、稳定、高效地分输到用户的问题，国内外学者从天然气分输控制和分输优化两个方面进行了大量的探讨。

分输控制方面，李立刚等采用改进的自适应广义预测控制进行分输压力控制，对系统模型进行在线辨识， 由辨识模型的阶跃响应系数计算G矩阵和预测向量， 避免了G矩阵不收敛且无需再进行Diophantine方程计算， 解决了天然气长输管网分输站用气量大范围波动、天然气调节阀死区较大引起压力控制不平稳导致的难以建立准确的控制模型、 控制参数难以整定等问题［1］。Hadian M等针对天然气分输管网压力控制滞后的问题，使用人工神经网络对天然气输气管网建模， 并采用布谷鸟优化算法训练神经网络的权值，采用模型预测控制，使得控制速度更快，误差更小［2］。 周湃等改进了天然气分输站场单路调压系统和多路调压系统的调节方法。 改进后，单路调压系统为先进行阀位调节，使阀后的流量或者压力接近所需要的设定值之后再进行流量或者压力微调；多路调压系统为一路调压装置设定为自动调节流量控制，其他路调压装置设定为手动调节。 改进后可有效提高分输效率，保护现场调压设备［3］。

也有学者从分输优化方面进行了一些有意义的探讨。 Rusnak D和Ferber P使用稳态优化模拟器对天然气输气管道进行了动态优化［4］，得到了在模拟时间内，天然气分输管道全线的能耗最小值。 但这种方法仅考虑能耗问题，并未将天然气输气管道运行收益最大化。 Park H J等对天然气田的生产过程进行了优化，针对影响天然气田生产的确定性因素采用模糊非线性规划的方法进行预测［5］。 针对天然气采气管径和产气井的生产效率采用遗传算法进行优化。 这种方法结构非常复杂，增加了求解难度，因此并不常用。 杨毅等以天然气分输管网系统运营部门的最大收益为目标，在管网节点的进（分）气流量、进（分）气压力、天然气分输管道能承受的最大压力、分输管网中压缩机站能提供的最大功率以及压缩机、天然气调节阀等非管道元件的模拟方程约束下，采用改进线性化算法，提高了求解速度［6］。这种方法考虑的约束更加全面， 但是计算过程非常复杂，增加了求解难度与求解时间。 刘武等以天然气压缩机运行过程中的最小费用为目标［7］，以压缩机站场的特性参数、管网的输送工艺数据及上游油气田产量等为约束条件，建立了天然气分输过程分输网管调度优化模型。 将遗传算法和差分进化算法结合进行模型求解，提高了收敛效果，得到网管运行过程中经过优化的调度方案。 这种方法在建模过程中仅考虑了压缩机费用的最小化，没有对整个天然气输气过程的费用进行优化，因此不能达到收益最大化。 彭赟等根据天然气的生产和销售是连续过程的特点， 使用动态规划理论，建立了天然气产销运行优化调度模型，利用遗传算法对模型进行求解，解决了天然气产销不平衡和运行不平稳的问题［8］。 这种方法按照月份对天然气进行调度优化， 没有考虑日指定小时分输。昂扬以各个天然气供气源的流量和压力平衡、天然气输气管道的水力运行条件及压缩机站的工作特性等为约束条件，建立了以天然气输气管网能耗最小为目标的模型，使用自适应动态规划法对模型进行求解［9］。 这种方法在建模过程中只考虑了能耗最小，不能保证整个天然气输气管网的收益最大化。 刘奇以天然气管道运行公司的收益为目标函数，以天然气不同的售气价格和管网压缩机能耗为约束， 建立天然气分输的优化模型。利用基于遗传算法优化的小波神经网络进行调度优化模型中压缩机功率和调度方案之间的建模，使用枚举法对优化模型进行了求解［10］。 这种枚举法寻优过程比较繁琐、计算量比较大。

以上所有这些探讨都没有考虑多种用户用气类型带来的用气规律的不同和日指定分输总量的约束性条件， 笔者即针对此问题展开研究。考虑不同用户类型售气价格不同，在满足天然气用户基本用气需求和用气安全的前提下以天然气公司售气收益最大为目标建立按小时进行分输的优化模型， 采用自适应遗传算法进行求解，得到最优日指定分输方案。

1 考虑多用户类型的日指定分输优化模型

求解实际优化问题时，需将实际问题抽象为最优化问题的数学模型，在此基础上求解，得到优化方案。 建立数学模型的过程中，考虑问题是否完善、模型是否合理是能否找到最优解的关键［11］。 求解最优化问题时建立的数学模型一般包含目标函数和约束条件，本项目中的目标函数即优化变量的函数，不同的需求对应不同的目标函数［12］。 求解时，优化变量取值有一定的限定范围，取值的约束在求解过程中称为解的约束条件。

1.1 目标函数与优化变量

目标函数为天然气销售公司售气收益F的最大化，在建模过程中考虑不同天然气用户的售气价格不同，对分输方案进行优化，得到下式：

式中 C1——每方天然气的购气成本，元；

C2——除购气成本之外的其他费用，元；

Pj——化学工业用户每方天然气销售价格，元；

Pk——不可中断工业用户每方天然气销售价格，元；

Pl——燃气公司每方天然气销售价格，元；

Pm——可中断工业用户每方天然气销售价格，元；

Sjt——第t个小时对化学工业用户的供气量，m3；

Skt——第t个小时对不可中断工业用户的供气量，m3；

Slt——第t个小时对燃气公司的供气量，m3；

Smt——第t个小时对可中断工业用户的供气量，m3；

St——第t个小时总的供气量，m3。

从收益模型可以看出，天然气售气收益等于向各个不同天然气用户供气量与相应天然气用户的售气价格的乘积的总和减掉购气成本和其他日常开销。 通过约束条件可以在满足不同天然气用户用气需求和安全用气的前提下，将更多的天然气输送给售气价格更高的用户，使得销售收益最大［13］。

1.2 约束条件

建立天然气日指定小时分输优化模型需要考虑的约束条件有： 管道所能允许的最大供气量、上游能够提供的最大最小供气量、用户小时最大用气量及保证用户用气的最小供气量等。 用户对天然气的需求非常大，但是天然气的供应量要受到产气量和天然气处理能力的约束，管网对所能允许的最大供气量也有一定的要求［14］。 因此，天然气的供气量只能在一定的约束范围内波动［15］。 除此之外，为满足用户的安全用气，也会根据用户的不同产生不同的供气约束：

式中 Smax——管线所能允许的最大供气量，m3；

Smin——保障输气压力的最小供气量，m3；

Sjtmax——第t个小时化学工业用户的最大供气量，m3；

Sjtmin——第t个小时化学工业用户的最小供气量，m3；

Sktmax——第t个小时不可中断工业用户的最大供气量，m3；

Sktmin——第t个小时不可中断工业用户的最小供气量，m3；

Sltmax——第t个小时燃气公司的最大供气量，m3；

Sltmin——第t个小时燃气公司的最小供气量，m3；

Smtmax——第t个小时可中断工业用户的最大供气量，m3；

Smtmin——第t个小时可中断工业用户的最小供气量，m3。

2 模型求解方法

自适应遗传算法（Adaptive Genetic Algorithm，AGA）是基本遗传算法的一种改进算法。 基本遗传算法存在收敛速度慢、收敛精度低、不稳定及容易局部收敛等缺点。 自适应遗传算法在寻优过程中能够自适应地调节交叉概率和遗传概率，更好地产生新个体，防止出现局部极值，从而搜索到全局最优解。 与现有的其他算法相比，自适应遗传算法全局寻优的收敛速度、求解精度有很大的改进和提高。 因此，笔者采用自适应遗传算法，对交叉概率和变异概率进行实时的调整［16，17］。

图1为自适应遗传算法的流程， 主要包括以下步骤：

a. 按问题的实际情况， 选择最适合求解的编码方法。 提供含有N个遗传染色体的初始种群。

b. 通过计算得到遗传算法中群体的染色体对应的适应度值，并进行适应度值调整。

c. 若某次运算过程中得到的解符合要求或者达到了最大迭代次数， 那么停止迭代计算，输出最优解。 否则，用随机的概率从现有的种群中选出一定的个体构成一个新的种群，继续进行迭代计算。

d. 对种群中的染色体进行交叉运算，得到新的个体。

e. 设置较小的变异概率，选择种群中某些染色体，进行变异运算产生新的种群。 重复步骤b。

图1 自适应遗传算法流程

交叉概率和变异概率的调整方式为：

其中p0为概率的初始值；pc为交叉概率；pm为变异概率；k1、k2为常数；Δf为max（f）-mean（f）。 由上述步骤，可以根据染色体的实际情况，自适应调整交叉概率和变异概率［18］。

3 案例验证

案例为中石化某油气公司2018年8月某一周的天然气销售运行情况。该油气公司用户有A（燃气公司用户）、B（可中断工业用户）、C（不可中断工业用户）、D（化学工业用户），每方销售价格分别为：2.85、3.67、3.97、2.65元。 所选取一周的天然气日计划销售量分别为：3.42×105、3.46×105、3.28×105、3.35×105、3.35×105、3.45×105、3.36×105m3。

染色体采用二进制编码方式， 表示4类用户一天每小时的供气量。 种群规模为50，遗传代数为100，初始交叉概率为0.9，初始变异概率为0.1。优化后得到7天的天然气按小时和按天汇总的供气量如图2所示。 4类用户分别的天然气日指定小时供气量如图3所示。

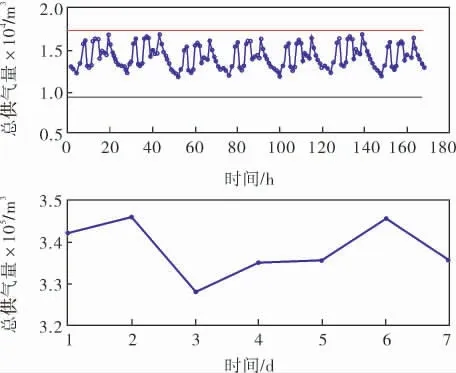
图2 优化后7天的天然气按小时和按天汇总的供气量

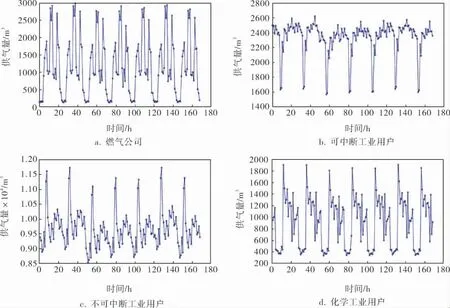
图3 优化后4类用户的小时供气量

图4是笔者所提分输优化法与综合权重法、改进剩余小时法的日指定分输方法获得收益的对比图。 由于到量停输法比较简单，没有经过任何优化，因此不具备对比价值。 改进剩余小时法优于剩余小时均量法，因此选择综合权重法和改进剩余小时法做了对比。 由图4可以看出，收益最高的为分输优化法，其次为综合优化法，最差的为改进剩余小时法。

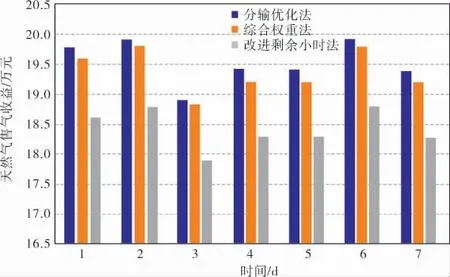
图4 不同分输方案的收益

4 结束语

研究了天然气日指定分输优化方案。 以天然气售气收益最大为目标，在满足天然气用户基本用气需求和输气安全的基础上，考虑不同用户售气价格不同的因素，建立了目标函数，采用自适应遗传算法对模型进行了求解。 结果表明：与现有的综合权重法、改进剩余小时法等分输方案相比，该方案能有效增加售气收入。