基于引力搜索算法的局部遮阴下光伏系统最大功率点跟踪算法研究

蒋鹏程 汤占军 刘萍兰

（昆明理工大学信息工程与自动化学院）

局部遮阴情况下，为了应对光伏阵列的热斑效应，在单块光伏电池处引入旁路二极管，导致一部分电池短路， 造成阵列输出的P-V特性曲线呈多峰形式，此时，将阵列外部电压控制在多峰曲线最大值所对应的电压可使输出的功率最大化，即最大功率点跟踪。 由于传统最大功率点跟踪（Maximun Power Point Tracking，MPPT）算法存在不能区分极大值与最大值的局限，使得阵列输出的功率往往只能跟踪到多峰曲线的极大值而不是最大值， 导致跟踪错误进而造成功率损失。针对该局部阴影下传统MPPT算法失效的问题，许多学者提出基于粒子群算法、遗传算法及蚁群算法等诸多优化算法［1～4］的MPPT控制方法，都能很好地实现最大功率点的跟踪控制。

引力搜索算法 （Gravitational Search Algorithm，GSA）［5］是一种新型群智能算法，该算法具有全局搜索能力强、收敛速度快等特点，常用于多分类数据集的分类、故障诊断等问题，但在以光伏MPPT控制为例的多峰曲线寻优方面应用较少［6］。 鉴于此，笔者将GSA与光伏系统的最大功率跟踪相结合，探讨它实现光伏MPPT的可能，利用MATLAB/simulink搭建仿真模型， 在不同环境条件下进行仿真分析， 对比它与电导增量法（INC）和模糊控制法（Fuzzy）的跟踪效果。

1 多峰光伏阵列模型

光伏阵列由多块光伏电池串联、 并联组成，现以3×1光伏阵列为例， 对其多峰特性进行仿真分析。

当光伏阵列局部被阴影遮蔽时，由于所受光照强度不同，被阴影遮挡的光伏电池的光生电流较小，相当于负载，损耗其他光伏电池所产生的功率，导致电池发热，减少电池的使用寿命。 对此， 通常引入旁路二极管短路被遮挡的光伏电池，以避免热斑效应［7］。

3×1光伏阵列如图1所示。 若光伏阵列各电池所受光照强度依次为1 000、800、600W/m2， 此时电池1、2、3对应的光生电流存在Iph1＞Iph2＞Iph3， 即电池2、3形成正向偏压，其旁路二极管导通，阵列输出电流为Iph1；当阵列受后级电路的影响，导致加在两端的电压逐渐升高，由于光伏电池输出的电流与电压成反比，此时Iph1逐渐减小，当阵列中各电池的光生电流变为Iph2＞Iph1且Iph2＞Iph3时，电池1、3形成正向偏压，其旁路二极管导通，阵列输出电流为Iph2；同理，当阵列两端电压持续上升至Iph3＞Iph1且Iph3＞Iph2时，阵列输出电流为Iph3。 光伏阵列的P-V特性曲线如图2所示，遮蔽情况下，其特征曲线呈现多峰［8］。

2 GSA算法

GSA是伊朗学者Esmat于2009年提出的一种新型群智能优化算法［9］。 标准的GSA以万有引力与牛顿第二定律为基础，认为：粒子间存在万有引力，质量越大且距离越近的粒子间引力越大，而粒子会在受其他粒子引力合力的方向上产生加速度， 该加速度的方向始终指向质量较大的粒子， 使得不同粒子向质量较大的粒子方向移动。 最终，质量最大的粒子的位置成为最优解。如图3所示，4个粒子之间存在万有引力，粒子M1受其他粒子引力F12、F13、F14的合力F1始终指向质量最大的粒子M3的方向， 并在该方向上产生加速度。

GSA中第i个粒子的质量Mi（t）的计算式为：

其中，mi（t）是第i个粒子相对于迭代中最好和最差适应度的占比，用于粒子质量的计算；N是粒子总数；fiti（t）是第i个粒子在t次迭代的适应度；best（t）、worst（t）分别是迭代时所有粒子中最好和最差的适应度，且根据优化目标的不同分为求解最大值问题与最小值问题，具体如下：

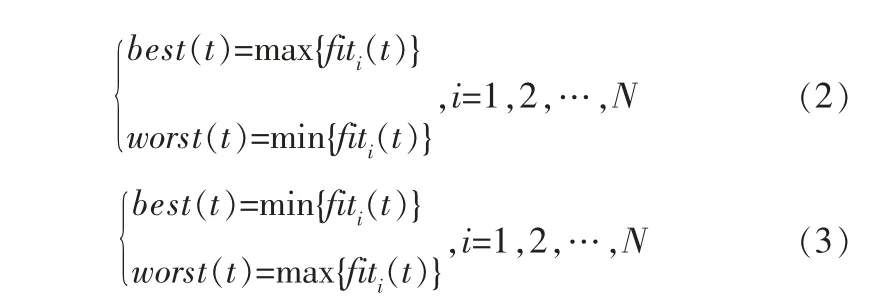
式中 G0——初始引力；

T——最大迭代次数；

α——衰减系数。

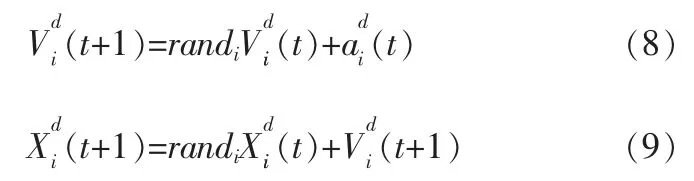
GSA算法步骤总结如下：

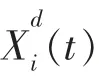
f. 重复步骤b～e，直到满足终止条件后，迭代结束。

3 基于GSA的MPPT控制算法

将引力搜索GSA应用于光伏系统MPPT控制方法中，利用群体中各粒子之间的万有引力相互作用产生的群体智能指导优化搜索［10］，来解决传统MPPT方法跟踪到极大值而不是最大值所导致的功率损失问题。

3.1 终止判定策略

为了能够在GSA优化中及时终止算法的迭代以减小输出功率的波动， 需要给GSA寻优设置终止条件。 在光伏系统MPPT控制中，光伏阵列输出的功率作为需要优化的目标在算法中代表粒子的适应值；占空比控制作为实现MPPT的方法在算法中代表粒子的位置；设置所有粒子间最大的适应值与位置的差值分别小于很小的阈值λ和θ时，认为MPPT完成，停止迭代。

3.2 重启条件

当外部光照情况改变时，光伏系统输出功率也会相应改变。 此时，最大功率点（MPP）发生偏移， 之前GSA迭代的位置所对应的工作点电压不再是当前MPP对应的电压，为减小功率的损失，需重启MPPT算法。

设置每隔一段时间采集阵列输出的功率，代入下式计算功率变化量ΔP：

ΔP是前后时刻的功率变化占比，反应功率的变化量。 对此，根据需要设置ΔP＞0.05时，重启MPPT算法。

3.3 算法流程

基于GSA的MPPT控制方法的算法流程如图4所示。

图4 基于GSA的MPPT控制方法的算法流程

4 仿真结果与分析

在MATLAB/simulink中搭建仿真模型，以验证基于GSA的MPPT算法的可行性。采用图1中3×1的光伏阵列搭建如图5所示的光伏系统模型，其单块光伏电池的参数为： 开路电压21.5V、 短路电流0.62A、峰值电压17.5V、峰值电流0.55A。

图5 光伏系统模型

图5中，Ipv、Upv为光伏阵列输出的电流和电压；电容Cpv介于光伏整列与Boost电路之间，起隔离干扰作用；Boost电路由电感L、绝缘栅双极型晶体管Q、二极管D和电容C共同组成，并在其后连接负载R。在局部遮阴情况下，对电导增量法（INC）、模糊控制（Fuzzy）和GSA算法的跟踪效果进行对比，并在光照突变情况下验证GSA算法的重启效果。

4.1 局部阴影情况下的仿真分析

两种局部遮阴情况分别设置如下：

a. 温度25℃， 光照强度依次为1 000、800、600W/m2；

b. 温度25℃，光照强度依次为1 000、500、1 000W/m2。

图6是在两种局部遮阴情况下的跟踪效果对比，具体数据见表1。

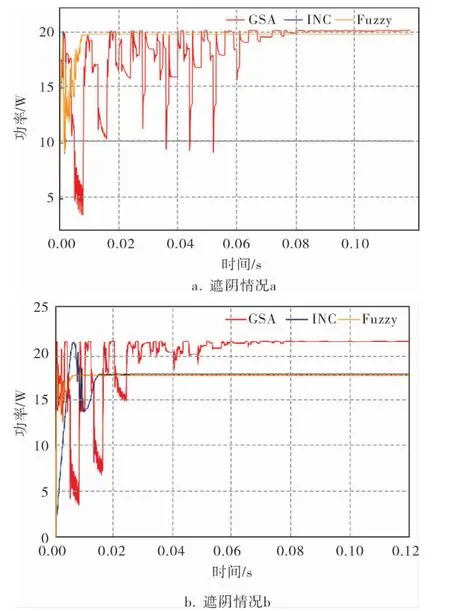
图6 局部遮阴情况下的仿真对比

表1 局部遮阴情况下的仿真数据

由图6、表1可知，两种遮阴情况下，基于GSA的MPPT方法分别在0.081、0.084s时跟踪到的最大功率分别为20.13、21.41W，相对于这两种遮阴下的标准最大功率20.14、21.56W，该跟踪方法使光伏系统输出的功率达到了标准功率的99.95%和98.05%。而传统的INC方法，虽然两种遮阴情况下跟踪均在0.02s内达到稳定，但它是收敛在局部极值而达到的稳定， 稳定时功率分别为10.22、17.24W，相较标准功率的差值较大，输出功率只达到标准功率的49.65%、79.96%。 Fuzzy方法，虽然在遮阴情况a 下在0.011s 时便稳定输出为19.83W， 输出功率达到了标准功率的98.46%，相对于GSA的跟踪效果相差无几，但在遮阴情况b时其输出功率稳定在17.24W， 只达到标准功率的79.96%，即收敛在局部极值。

综上所述， 局部遮阴情况下， 传统的INC与Fuzzy虽然能快速实现跟踪，但存在错误跟踪的风险，造成功率损失。 证实基于GSA的MPPT算法相比于传统MPPT算法，能实现精确跟踪，从而减小功率的损失。

4.2 光照突变下的仿真分析

为验证光照突变时算法的跟踪效果，在遮阴情况a跟踪0.1s时切换到遮阴情况b， 其仿真结果如图7所示，具体数据见表2。

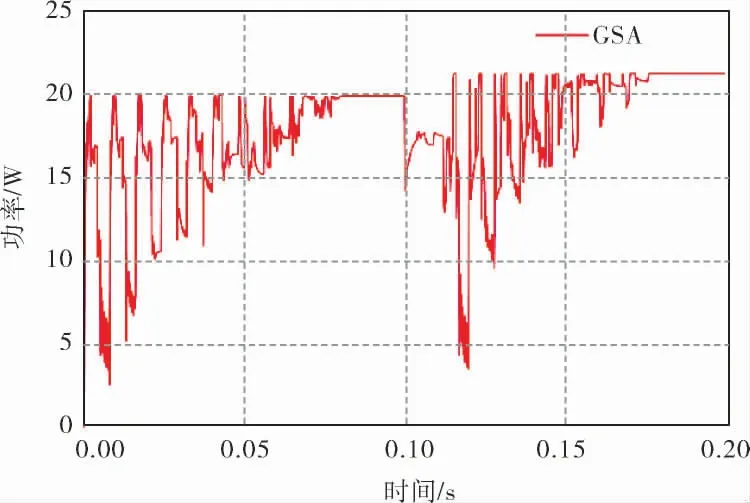
图7 光照突变下的仿真结果

表2 光照突变情况下的仿真数据

由图7、表2可知，遮阴情况a下GSA算法通过0.081s的更新迭代，跟踪到最大功率19.97W，即此时标准输出功率的99.16%；0.10s时阵列所受光照条件改变，之前跟踪稳定的工作点在新的遮阴情况下输出的功率为17.35W，代入式（10）计算得ΔP≈0.13，满足截止条件，算法重启，0.078s后跟踪到新的最大功率21.34W，即此时标准输出功率的98.98%。 两种遮阴情况下均能实现精确跟踪，且光照突变时算法能自动重启，重新跟踪到新遮阴情况下的最大功率点。

5 结束语

针对局部遮阴情况下传统MPPT算法在光伏阵列最大功率点跟踪控制时失效的问题，提出以GSA算法为基础的MPPT算法，该算法依据群体中各粒子之间的相互引力与该引力作用下产生的加速度，来指导优化搜索，以避免跟踪陷入局部最优。 仿真结果表明：GSA算法相较于以INC和Fuzzy为代表的传统控制算法，能够避免错误跟踪的风险，实现光伏阵列最大功率精确跟踪，从而提高发电功率。