线性规划布局模型在葡萄种植中的应用
李强 雷晓军 虎良荣 阮兰仓


摘 要 现代农业规模化种植中,在条件不变的情况下,统筹安排、合理布局是使总的经济效果达到最佳的科学方式,是提高农业产量的有效方法之一。基于此,结合贵州省铜仁市现阶段农业现状及铜仁市川硐镇乌泥村葡萄种植情况,运用线性规划就如何布局使其葡萄产量最佳进行分析,并给出葡萄种植的一般布局模型、解法及应用推广示例。
关键词 线性规划;布局模型;农业;葡萄种植;合理布局
中图分类号:F22 文献标志码:B DOI:10.19415/j.cnki.1673-890x.2020.09.090
在社会生产活动中,运用数学分析方法是提高经济效果的科学方式。进入21世纪,随着应用数学的高速发展,数学分析方法的运用在农业种植中的作用越来越明显。特别是在规模化种植越来越普遍的现代农业种植中更具有不可或缺的作用。曾有过一系列关于线性规划在经济中应用的理论成果[1]。
在研究规模化种植业的活动中,因地制宜、合理布局、确定各种品种及不同作物在土壤上的种植面积,完成种植计划的同时,使总产量达到最大是现代农业生产的基本要求,也是规模化种植业所面临的巨大挑战。基于此,结合铜仁市乌泥村葡萄种植的实际情况,就规模化葡萄种植布局进行分析。
1 铜仁市农业生产发展概况
基于党和政府制定的一系列惠农政策,我国农业呈现出全面、稳定、协调发展的良好态势。但与发达国家和现代农业发展的要求相比,我国农业生产发展的水平依然较低,生产组织化程度及规模化程度不够。调整农业生产结构,使产业布局不断优化,全面提高农村农业规模化、高度现代化是我国农业发展的必然趋势[2]。
随着新农村建设的推进,铜仁市新农村试点建设取得了一系列成就。但就总体而言,依然面临以下3个方面的问题:1)外来商收购农特产品时,只有特色没有数量和质量;2)本地农户不敢大量种植,担心销路;3)种植碎片化,规模化不够。加强科技下乡,支持铜仁市“三农”事业发展,是改变这种现状行之有效的手段之一,也是实现铜仁市农业现代化发展的基本要求[3]。
2 预备知识
线性规划一般形式[4-5]为maxZ=C1x1+C2x2+…+Cnxn,使得
其中xj(j=1,…,n)为决策变量,为目标函数。
线性规划模型的常见解法有单纯形法、图解法、两阶段法以及对偶单纯形法[6-7]。
线性规划问题解的基本性质:1)所有可行解构成的集合称为可行域;2)如果集合k中任意两点s、t之间连线上的点都是集合k中的点,即对于任意的s、t∈k,都有θS+(1-θ)t∈K(0≤θ≤1),则称k为凸集;3)设k是凸集,x∈K,若x不能用不同的两点x1∈k和x2∈k线性表示成x=θx1+(1-θ)x2(0≤θ≤1),则称x是k的一个顶点(或极点);4)线性规划问题的基本可行解对应于可行域的顶点。
为了叙述讨论的方便,作出如下規定:1)任何一编号区域内的土壤成分相同;2)同一种作物的不同品种均视为不同品种的作物;3)播种面积不得大于土地面积,且作物的种植面积非负。
对模型作如下2点说明:1)所有讨论均是在光照、管理、水分等其他条件不变的情况下,即研究相同成分的土壤对不同品种作物的生长情况;2)所涉及数据均来自农民口中,所涉及数据可靠性较低。
3 布局模型及应用
3.1 种植布局模型
为了改变铜仁地区葡萄种植面临的问题,扩大种植规模,进行如下的布局讨论。一般地,假设将要在B1,B2,…,Bn这n块土地上种植m中不同品种的葡萄A1,A2,…,Am。根据多年来的经验,可知各葡萄在各土地上的产量。据此作出葡萄种植计划如表1所示(产量单位:kg·hm-2)。
表1中:ai表示葡萄Ai今后的计划种植面积(i=1,2,…,m);bj表示土地Bj的作物种植公顷数(j=1,2,…,n);Cij表示在土地Bj上种植葡萄Ai的产量(i=1,2,…,m,j=1,2,…,n)。
用线性规划的方法来研究这一实际问题,根据规定,计划播种总的面积不得大于土地的实际面积,即需满足公式1。
假设xij(i=1,2,…,m,j=1,2,…,n)为土地Bj上种植葡萄Ai的公顷数,在各块土地上种植葡萄Ai的公顷数应小于等于Ai的计划播种公顷数,即应满足公式2。
又因为种植面积不大于土地原有面积,即在土地Bj上种植各葡萄的公顷数应小于等于Bj的面积,于是有公式3。
其中,xij应满足公式4。
于是,在满足公式1~4的情况下,求一变量xij(i=1,2,…,m,j=1,2,…,n)的值,使达到最大值,这样就可以得到一个关于线性规划的布局模型,使得:
在这里,记模型Ⅰ的约束系数的约束矩阵为A,右端向量为b。其中,
由于,在结合实际种植时,应尽量利用土地这一客观事实。可以证明,A的秩至多为m+n-1,因此A至多有m+n-1个线性无关的列。因此,布局模型Ⅰ的任意一个基本解都至多有m+n-1个基变量。这m+n-1个基变量对应的值就是一种葡萄的种植方案,在众多方案(即众多解)中一定存在一个最优解,在满足种植计划的前提下,使总的产量最多。而求出这个最优解,就是对应的合理布局。
3.2 最优布局模型的解法
考虑实际种植情况,不妨设种植模型Ⅰ的可行区域D={x∈Rn|Ax=d,x≥0},其中A为模型Ⅰ的约束系数的约束矩阵,b为右端向量,x为一个满足所有约束条件的向量[8-9]。其中,x=(x11,…,x1n,x21,…,xmn)T,b=(a1,…,am,b1,…,bn)T,
有以下3条定理。
1)种植模型的可行区域D={x∈Rn|Ax=d,x≥0}是凸集。证明:?x,y∈D,有W=θx+(1-θ)y,其中θ∈[0,1],又x≥0,y≥0,Ax=d,Ay=d,故AW=θAx+
(1-θ)Ay=d,即W∈D。
2)种植模型可行域中的顶点是有限的,而这些顶点就是对应的种植模型的基本可行解。
3)种植模型的基本可行解是有限的,且有限的基本可行解中至多有有限个最优解。
事实上,由组合的知识可知,在n块不同土地上种植m种不同的葡萄,可确定不超过(nm)种不同的方法;另一方面,可以根据种植计划把现有土地分成与种植计划相同的块数,在实际中,这种方法是有限的。
结合定理1、2,可以知道种植模型一定存在一个基本可行解是最优解,而这个最优解就对应一种最佳的布局方案。可以用常见的线性规划解法及数学软件Lingo来求布局模型的最优解。
3.3 葡萄种植应用举例
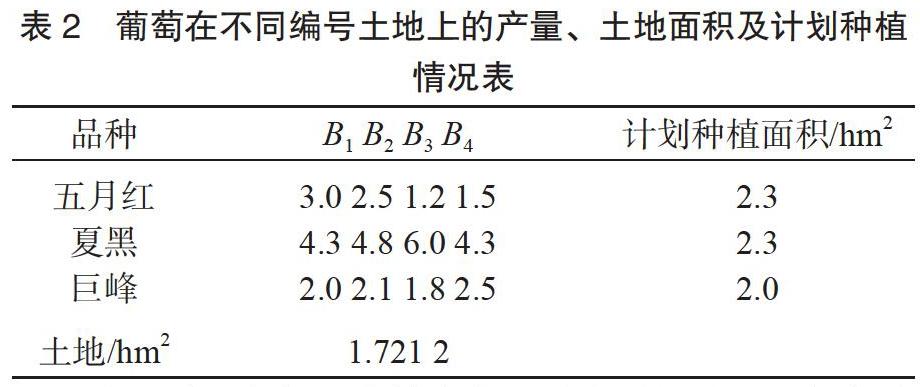
为了说明布局模型Ⅰ的合理性及可行性,结合铜仁市川硐镇乌泥村葡萄种植情况,运用模拟数学实验的方法来进行布局浅析。1)在乌泥村选取4块土壤成分不同的土地各100 hm2,而每一块土地的土壤对同一种葡萄的生长影响一致,设这4块土地分别为B1、B2、B3、B4。2)选定五月红、夏黑、巨峰3中优良葡萄进行种植。结合以往葡萄种植经验,不同葡萄在不同编号土地上的单位产量、土地面积及计划种植情况见表2。
为了讨论方便,并结合实际种植时的需要,假定计划种植面积与土地实际面积相等。
令xij(i=1,2,3,j=1,2,3,4)分别为五月红、夏黑、巨峰在B1、B2、B3、B4这4块土地上的种植面积,并用Z来表示3种葡萄的总产量。由模型Ⅰ可知,在完成种植计划的前提下,总产量最大,即说明布局合理。于是,有以下結果。maxZ=3x11+2.5x12+1.2x13+1.5x14+4.3x21+4.8x22+6x23+4.3x24+2x31+2.1x32+1.8x33+2.5x34
使用Lingo来求解布局模型Ⅱ,解得x11=1.7,x12=0.7,x22=1.3,x23=1,x34=2,Z=24 067。
于是,得到一组变量x=(1.7,0.7,0,0,0,1.3,1,0,0,0,0,2),
表示在编号为B1的土地上种1.7 hm2五月红,在编号为B2的土地上种0.7 hm2五月红,在编号B2的土地上种1.3 hm2
夏黑,在编号B4的土地上种2.0 hm2巨峰为最佳的布局方案。此时,在往年其他情况(如管理、光照、水分等)不变条件下,葡萄总的产量预计为315 500 kg。于是得到最优布局如表3所示。
考虑葡萄种植的长期性,将编号为B2的土地分成B21和B22两块。其中,B21=0.7 hm2,B22=1.3 hm2,于是,就得到所要的最佳布局方案及预期产量表4。
4 布局的推广
结合实际不难发现,该模型在水果、农产品和蔬菜等种植中均有重要的作用,如在蔬菜大棚种植蔬菜时可根据市场需求量及土壤情况,选择最佳的土壤来种植。同时也可为制定铜仁地区未来农业发展方向提供参考。
5 结论
随着科学技术的不断发展,未来农业一定会走向规模化发展的道路,葡萄种植也是如此,而科学合理的布局是未来农业发展的有力武器。笔者在实际考察的基础上给出了不同土壤中不同作物生长情况的一般布局模型,并进行了简单的应用举例和应用方向的推广,促进了葡萄规模化种植中线性规划布局模型的应用。
参考文献:
[1] 雷晓军,梁治安.证券组合投资模型优化[J].商场现代化,2007(24):171-172.
[2] 付海兰,雷晓军.网络环境下职业技术教育立体化教学的构建与实践[J].中国大学教学,2011(8):39-41.
[3] 张勇.新农村建设长效机制探索——对铜仁地区新农村建设的社会人类学调查及思考(上)[J].铜仁学院学报,2008,10(3):54-58.
[4] 刁在筠,刘桂真.运筹学[M].北京:高等教育出版,2007.
[5] 《现代应用数学手册》编委会.运筹学与最优化理论卷[M].北京:清华大学出版社,2001.
[6] Winston W L.运筹学概率模型应用范例与解法[M].北京:清华大学出版社,2006.
[7] 孔祥智.2009中国“三农”前景报告[M].北京:中国时代经济出版社,2009.
[8] 焦宝聪,陈兰芝.运筹学的思想方法及应用[M].北京:北京大学出版社,2008.
[9] 邢文训,谢金星.现代优化计算方法[M].北京:清华大学出版社,2001.
(责任编辑:赵中正)
收稿日期:2020-02-15
作者简介:李强(1977—),男,贵州松桃人,硕士,副教授,研究方向为数学教育与数学建模。
为通信作者,E-mail: 1132129812@qq.com。

