热防护服热传导过程的仿真研究
陈波红 覃月宁


摘 要:在高温环境下作业的工作人员,着装时既要考虑服装的功能性,也要考虑其舒适性。基于此,本文针对由三层不同材料的热防护服及空气层共四层的热防护系统建立热传导模型,并利用有限差分计算、仿真模拟假人皮肤表层的温度分布。其次,本文利用二分法,并编程模拟仿真得到当外界温度为65℃,作业时间为60min,皮肤表层温度不超过47℃且超过44℃的时间不超过5min时,热防护服第2层的最优厚度设计值为19.09mm。
关键词:热传递模型;有限差分;最优厚度设计;仿真模拟;二分法
0 引言
在消防、炼铁、陶瓷制造等高温作业环境中,工作人员必须穿着专用的热防护服工作,以免被灼伤。特别是消防人员,必须穿着热防护服才能进入高温环境中作业。考虑到消防人员作业时,要便于行动但不便穿着太厚重的服装进行作业,热防护服也存在热传导,作业时间有限。因此,本文介绍热防护服的热传导模型并给出热防护服最优厚度的设计方法,是必要且有社会价值的。
近年来,关于防护服热湿传递模型的研究已成为热点。根据热防护服制作是使用单层一种材料还是多层多种不同材料,热传递模型分为单层模型和多层模型。基于热传递单层模型的研究,很多学者给出了热防护服热传递的多层模型。Mell等[1]提出了包含热传递及热辐射的多层材料热传递模型;鉴于湿热水气对热传递的作用,Lawson等[2]建立了多层织物的热湿传递模型;由于空气层对热防护服的防护效果有显著影响,Ghazy等[3]建立了防护系统中包含空气层的多层织物的热传导模型。
本文综合上述的研究,给出热防护服包含多层材料及空气层的多层热传导模型及該模型的仿真研究。如图1给出由三层不同材料构成的热防护服、防护服与人体皮肤间的空气层、人体皮肤组成的防护系统,根据热防护服所使用的纺织材料的特性,通常第1层的厚度为0.6mm,第2层的厚度在0.6~25mm之间,第3层的厚度为3.6mm,第4层的厚度在0.6~6.4mm。
1 热传递模型
为设计专用的热防护服,现将体内温度控制在37℃的假人放在设定的高温实验室环境里,针对外界环境温度为75℃,假人第2层厚度为6 mm、第4层厚度为5 mm且工作时间为90min的条件下进行实验,测量得到假人皮肤外侧的温度。
本文将建立热传导模型,仿真计算假人皮肤表层的温度分布,并将得到的数据形成仿真图表。为了简化模型,把热传导看做只有由外界向皮肤侧一个方向的热传导。
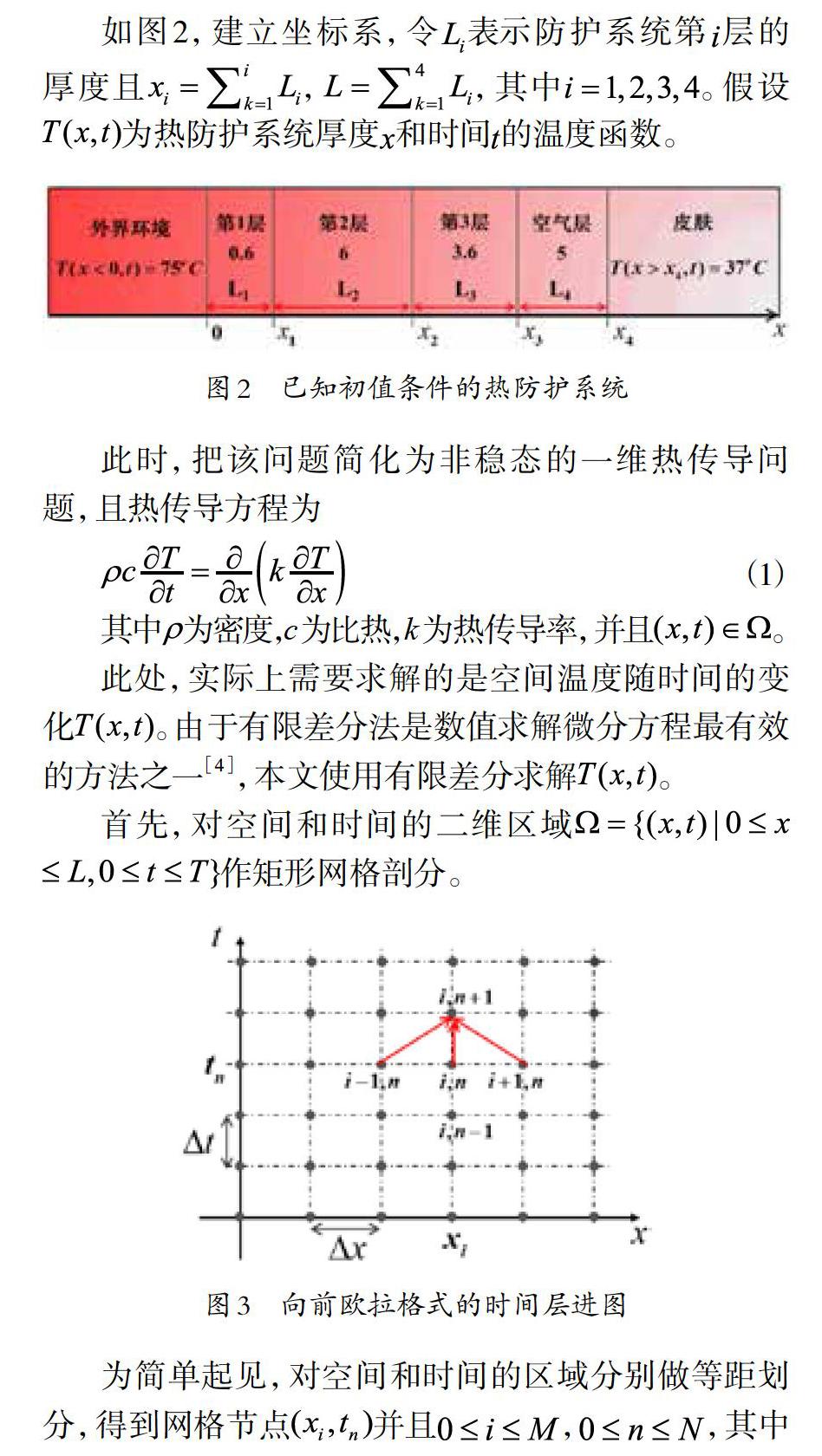
如图2,建立坐标系,令表示防护系统第层的厚度且,,其中。假设为热防护系统厚度和时间的温度函数。
由式可知,给出了n时间步和n+1时间步温度场的关系表达式。可知,只要n时间步的温度场知道,就由此可求得n+1步的温度场,即可得到所有网格点的数值解。
2 模型的求解与仿真
假设热防护服各层材料的参数如表1,初始条件,根据表格中的参数利用Matlab进行编程仿真模拟[5]。
可得,图4为利用有限差分获得的稳态时温度分布数值解,图5为不同时刻的空间温度分布,图6为仿真模拟得到的数据与实验数据的拟合图。
由图6可知,仿真模拟得到的温度数据与实验数据之间的误差很小,说明上述建立的热传递模型切合实际。
3 热防护服某层厚度的最优设计
如今假定热防护系统中的,当外界环境的温度为65℃,为确保工作人员的作业时间为60min,作业时间内,假人皮肤外侧温度不超过47℃且超过44℃的时间不超过5min,下面给出热防护服第2层的最优厚度。
以外界环境温度恒为65℃,皮肤的外侧温度要求小于47℃,且皮肤外侧温度超过44℃的时间小于5min为约束条件,建立单一变量的优化模型并求的最小值。假设为温度分布函数。故上述问题转化为如下的优化模型:
初始条件为℃,假定系统第2层厚度分别为12.8mm和25mm,得到假人皮肤表层的温度变化,如图7、图8。由图可知,时,30min时假人皮肤表层的温度已到达44℃,不满足约束条件;时,60min后假人皮肤表层的温度尚未到达44℃,不满足约束条件,为了兼顾热防护服的制作成本和舒适性,此厚度也不是好的方案。
本文利用二分法给出最优值的算法,令计算精度 。算法如下:
第1步,取0.6mm,计算系统的温度分布。
如果满足上述约束条件,则第2层的最小厚度0.6mm,算法结束。如果不满足上述约束条件,取,算法转第2步。
第2步,取,计算系统的温度分布。
如果不满足上述约束条件,则所用材料不满足要求,算法结束。如果满足上述约束条件,取,转第3步。
第3步,若,则第2层的最优厚度取为。否则,转第4步。
第4步,令,计算系统的温度分布。如果满足上述约束条件,取,
转第3步。如果不满足上述约束条件,取,
转第3步。直至得到的取值满足假人皮肤外侧温度不超过47℃且超过44℃的时间不超过5min。
利用Matlab编程可得,满足约束条件的第2层最优厚度为。图9给出了满足约束条件的假人皮肤的温度随时间变化的曲线。
4 结束语
本文针对由三层不同材料的热防护服及空气层共四层的热防护系统建立热传导模型,并将模型离散化,进而利用有限差分法求解模型。基于该模型,得到的假人皮肤表层温度的模拟数值,并将模拟数值与假人实验数值进行分析、比较,两组数据之间的误差极小,说明本文建立的热传递模型是切合实际的。另外,本文利用二分法,编程模拟仿真外界温度为65℃,作业时间为60min,作业时间内假人皮肤表层温度不超过47℃且超过44℃的时间不超过5min时热防护服第2层的最优厚度为19.09mm。这给制造热防护服的设计者提出了很有价值的参考,同时也减少了热防护服制作的材料成本和时间成本。
参考文献:
[1]Mell W E, Lawson J R. Heat transfer model for fire fighters protective clothing [J]. Fire Technol, 1999, 36:39-68.
[2]Lawson J R, Mell W E,Prasad K. A Heat Transfer model for firefighters protective clothing:continued developments in protective clothing modeling[J]. Fire Technol, 2010, 46(4):833-841.
[3]Ahmed Ghazy, Donald J. Numerical simulation of heat transfer in firefightes protective clothing with multiple air gaps during falsh fire exposure[J]. Numerical Heat Transfer Applications, 2012, 61(8):569-593.
[4]花冬英, 李祥贵. 微分方程的数值解法与程序实现[M]. 北京:电子工业出版社, 2016..
[5]卓金武, 王鸿钧. MATLAB数学建模方法与实践(第3版)[M]. 北京:北京航空航天大学出版社, 2018.

