基于松弛算法的停机位分配优化方法

邢志伟，乔 迪*，刘洪恩，高志伟，罗 晓，罗 谦

（1.中国民航大学电子信息与自动化学院，天津 300300；2.中国民航局第二研究所工程技术研究中心，成都 610041）

（∗通信作者电子邮箱331746800@qq.com）

0 引言

随着近年来旅客吞吐量和飞机起降架次逐年增加，航班延误对机场运行的扰动日益严重。停机位资源的分配是机场运营管理的重要环节之一，合理的机位资源分配方案是减少冲突、提高机位利用率的重要途径。在航空需求无限增长与机位资源有限的不均衡现象日益突出的情况下，如何在减少航班延误或提前到达对机位分配方案产生的冲突的同时又提高机位利用率是机场运行亟待解决的问题。

目前，已有很多国内外学者分别从不同的角度对机位分配问题进行了深入研究。李亚玲等［1］以最大化停机位利用率和最小化旅客行走路程为优化目标，提出了能够动态、灵活进行机位分配的禁忌搜索算法；Yu等［2］从缓冲时间成本、设备及工作人员调度成本、旅客满意度等方面进行建模，并通过将二次模型转化为等效的混合整数规划（Mixed Integer Programming，MIP）模型用启发式算法进行求解；Liu 等［3］以最小化空闲时间段和远机位数为优化目标，设计相应的遗传算法；Behrends 等［4］考虑了因旅客登机及货物运输对航班造成延误影响并设计遗传算法求解；Deng 等［5］通过分析停机位和航班特点，以空闲时间均衡、旅客行走距离最短、远机位数最小为目标，设计了一种改进的蚁群优化算法；Stollenwerk 等［6］以旅客总的换乘时间最短为优化目标，设计量子退火方法进行求解，但是只能解决小范围的问题，当范围过大时花费的成本较高；冯霞等［7］考虑了航班在推出-滑入机位时在滑行道存在的冲突情况，在模型中添加防冲突约束，并设计了禁忌搜索算法求解。以上研究均未考虑航班延误对机位分配结果的影响，且旅客的行走距离、旅客换乘时间等数据不易在机场实际运行中准确地获取。从提高鲁棒性的角度出发：李军会等［8］通过分析航班延误分布，以机位冲突概率最小为目标，设计贪婪禁忌搜索算法；Kumar 等［9］从新的角度出发，提出了以区域使用成本最小、运营收入最大、机位分配的鲁棒性这几个角度出发进行设计；刘君强等［10］以最小延误费用原则为约束，采用混合集合规划进行指派模型的建立与求解；Dorndorf 等［11］以最小化机位冲突为目标，将此问题看作是区域划分问题来求解，在设计过程中没有像其他研究一样建立虚拟停机位；杨新湦等［12］以机场运行系统扰动最小为优化目标，建立停机位与滑行路径临时改派双层模型；Kim 等［13］通过分析航班到离港情况建立了避免冲突的鲁棒性模型；Van Schaijk 等［14］提出了一种将确定的机位约束由随机机位约束替换的方法，并建立了线性规划模型，验证了该方法具有较好的鲁棒性。

以上大部分研究都是从鲁棒性、旅客行走距离、换乘时间等方面进行研究，未考虑到机位利用率与鲁棒性的关系。本文综合考虑了停机位的利用率及鲁棒性，提出了一种新的停机位分配方法，通过分析航班到达的分布特点，设计同机位相邻航班间的缓冲时间，并考虑运行中的相关约束，建立停机位分配模型。针对该分配模型的特点采用拉格朗日松弛算法对其进行仿真模拟优化，并与实际机场运行数据进行验证和对比，说明本文所提出的方法能够较好地提高机位利用率，并减少航班冲突数量。

1 停机位分配模型

1.1 问题描述与模型假设

机场停机位分为近机位和远机位，近机位配有廊桥，乘客上下飞机方便，乘客在远机位登机则需要借助摆渡车，不但给旅客带来不便，而且增加机场运营成本。停机位分配是指将有限的停机位资源合理地分配给某个时间段内的到港航班，兼顾旅客登转机时间、航班地面服务时间、航班类型、航班时刻、停机位类型等因素，最终实现对未来某个时间段内的到港航班分配合适的停机位，并且在分配过程中力求提高机场运行效率、减少运营成本，同时又能提高旅客满意度。

不失一般性，需要解决的问题可以描述为：存在m个停机位为航班停靠及旅客登机服务，选取的时间段内有n个航班需要停靠在机位上。稳定性是反映停机位分配方案鲁棒性的指标，即停机位分配方案在受到扰动后的偏离程度，假设QA为实际运行时偏离停机位分配方案的航班数量，n为总的航班数量，则可用QA/n的值来评价分配方案的鲁棒性。如果在同一机位相邻两航班间的时间间隔较大时，前序航班产生的延误对后续航班的影响较小，则QA/n的值越小鲁棒性越好；反之，若两航班间的间隔过小时，前序航班产生的延误对同一机位后续航班的影响较大，则QA/n的值越大鲁棒性越差。另一方面，如果两航班间的间隔时间较大，虽然鲁棒性很好，但是会造成资源浪费，因此如何合理地进行设计是一个关键问题。航班j和航班i是分配在同一机位的两个航班，且航班j是航班i的紧后航班，[di，aj]表示航班i和j间的空闲时间窗。结合机场运行实际需求，设定停机位分配的优化目标如下：

1）最小化每个停机位的空闲时间，即所有停机位的未被占用时间总和最小。

2）最小化远机位的占用时间，即尽可能把航班分配到近机位，最小化远机位个数，从而既方便旅客登机又减少摆渡车等的费用。

本文研究停机位分配问题，基于如下假设：

1）机场停机位数量充足，在某时间段内不会出现航班无机位可分配的情况；

2）不考虑某些特定区域机位指定给某固定的航空公司使用；

3）进港航班均服从“先到先服务”的原则；

4）航班计划信息完备已知，包括航班机型、到离港航班时刻计划等；

5）不考虑某些停机位因设备故障等特殊原因而导致的不可用的情况。

1.2 模型构建

1.2.1 符号变量说明

停机位分配模型所使用的符号参数说明如下：

1）输入变量：N为航班集合；M为停机位集合；εi为航班i的飞机型号；ρk为机位k允许停放的最大机型；TP为同一机位相邻两个航班间的最小安全缓冲时间；ai为航班i的到港时间；di为航班i的离港时间；ti为航班i在远机位的停放时间；Tik为机位k相邻两航班间的空闲时间；U为航班过站时间；i，j=1，2，…，n，i≠j；k=1，2，…，m；飞机型号为｛1，2，3｝；停机位大小为｛A，B，C｝，分别代表大型、中型、小型停机位。

2）决策变量：yik为机位k是否指派给航班i，yik=，i=1，2，…，n，k=1，2，…，m；Zi为航班i是否被分配到远机位，；yijk为相邻两航班i、j是否被分配到同一停机位k，同时i＜j，yijk=。

1.2.2 优化目标

根据上述分析，停机位分配模型的优化目标如下。

1）最小化各机位空闲时间为：

2）最小化远机位占用时间为：

1.2.3 约束条件

如果航班i和航班j为同机位的相邻航班，则两航班间要有安全缓冲时间，需要满足：航班i离港时间-航班j进港时间≥最小安全缓冲时间；如果航班i和航班j为同机位的紧前紧后航班，可以推算两航班间的空闲时间应小于航班过站时间：航班i离港时间-航班j进港时间≤航班过站时间。综上停机位分配模型的约束条件如下：

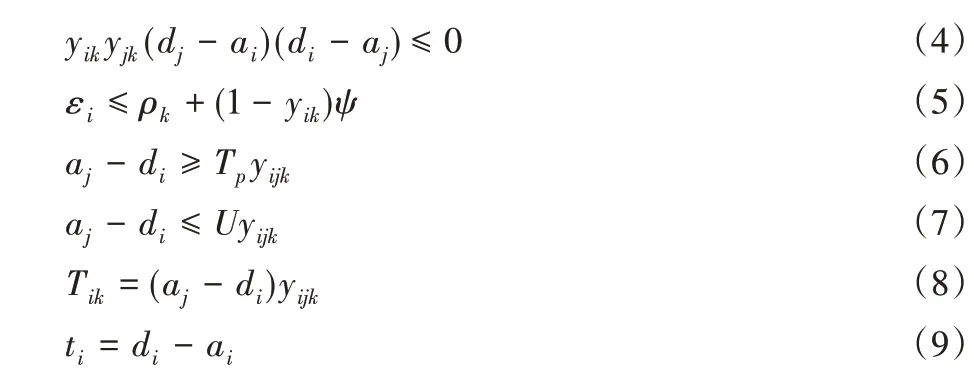
式（3）表示每架航班只能且必须分配一个停机位。式（4）表示同一停机位在同一时刻只能停放一架飞机，分两种情况：1）航班i先被分配到停机位k上，航班j后被分配到停机位k上，即ai＜di＜aj＜dj；2）航班j先被分配到停机位k上，航班i后被分配到停机位k上，即aj＜dj＜ai＜di。式（5）表示机位大小与机型的约束，ψ为一个足够大的正整数。式（6）表示分配在同一机位的相邻两架航班的最小缓冲时间约束。式（7）表示分配到同一机位的两航班间隔时间与过站时间的约束。式（8）表示机位空闲时间。式（9）表示航班占用机位时间。

2 基于双目标松弛算法的停机位分配模型

根据1.2 节的介绍，停机位分配调度模型是一个典型的NP（Non-deterministic Polynomial）-hard 混合整数规划问题，拉格朗日松弛算法可以通过将机位分配问题中的困难约束条件松弛到目标函数中，从而降低模型的求解难度。同时通过求解松弛问题，可获得原问题的解的上下界，然后对拉格朗日乘子进行不断的迭代更新，使得松弛问题的解逐渐逼近原问题的解。

2.1 拉格朗日对偶解的分析

假设zIP为本文机位分配中的目标函数，zLR为将机位分配模型中的某个约束条件进行松弛后其对应的松弛问题，由于约束条件松弛，解空间范围增大。这时，zLR为使得近机位空闲时间和远机位占用最小解的下界，zLD为原问题的拉格朗日松弛对偶问题。若松弛问题存在可行解，则有ZLR≤ZLD≤ZIP表示其对应问题解的一个值。为了更好地接近原问题的最优解，因此用机位分配问题的拉格朗日对偶问题的对偶解来代替机位松弛问题的解。证明如下：

有限个离散点的集合Q={x|Bx≥d，x∈}是该问题的解集，且可证明Con(Q)为凸集。

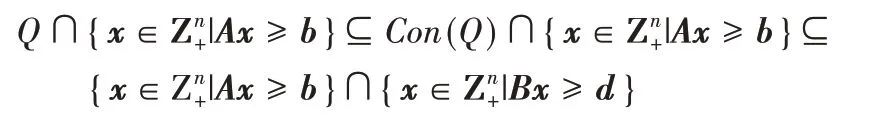
得到：

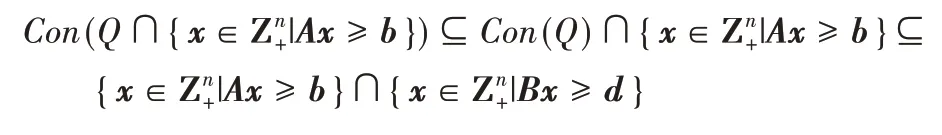
若zLD的目标值有界，则

s.t.Ax≥b（松弛约束）

即zLD=min{cTx|Ax≥b，x∈Con(Q)}，所以有：

然后在已知的可行解域中对凸函数使用次梯度算法通过不断的迭代求得全局最优解。

2.2 机位分配问题的拉格朗日对偶松弛问题

对机位分配模型中的约束式（3）松弛，则原问题变成了不考虑机位约束的问题。松弛后的模型相较于原模型约束条件减少一个，限制因素减弱，即解空间增大。拉格朗日松弛算法是一种求最值问题很有效的方法，设λi是非负的拉格朗日乘子，zLR为机位分配问题的拉格朗日松弛问题，则有：

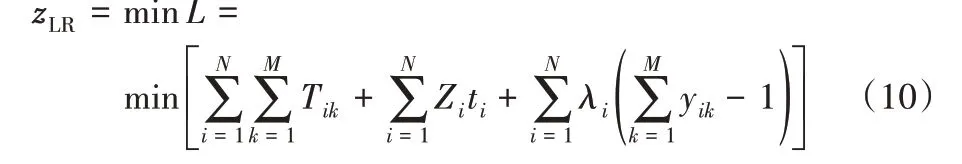
上述目标函数需满足式（4）～式（9）和式（11）：

记zLD为原问题的拉格朗日松弛对偶问题，则有：

将式（13）的拉格朗日松弛对偶问题分成两部分：式（14）为非正则子问题；式（15）为正则子问题。当给定一组拉格朗日乘子λi时，式（14）为一个确定的值。正则子问题可基于不同航班进行分解。

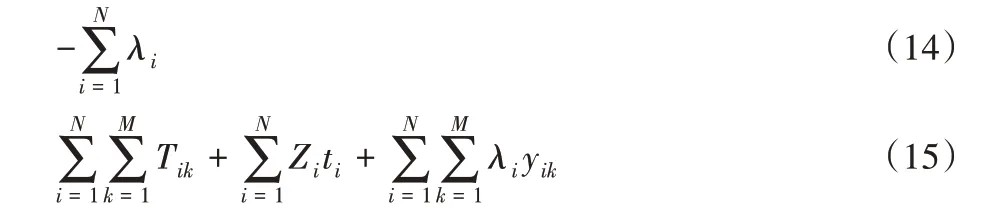
正则子问题可以给予航班分解：

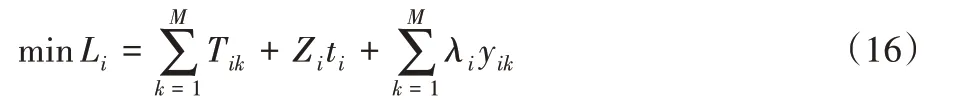
其中，λi反映了航班占用机位k所需要付出的代价，占用不同的机位需要付出相应的代价。式（16）的目标是确定航班占用的机位及其空闲的时间，使其占用机位所付出的代价和空闲时间总和达到最小。

2.3 次梯度算法优化拉格朗日乘子

次梯度算法是一种求解拉格朗日问题的有效方法，Tik、Zi、ti、yik可以通过子问题的求解过程得到。

式（17）中拉格朗日乘子的初始值为0，上标u表示迭代次数。Si表示拉格朗日乘子λi的次梯度方向，如式（18）所示：

θu表示第u次迭代的步长，如式（19）所示：

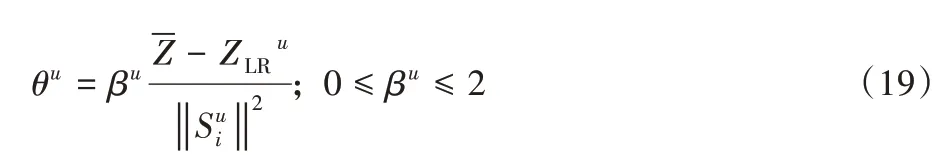
2.4 构造可行解

对偶问题得到的解对原问题来说可能是不可行的，因为可能不符合唯一性的约束条件（3），因此需要对松弛问题的解进行可行化，从而获得原问题的上界。本文设计了一种启发式算法，其步骤如下：将式（16）求得的解作为启发信息，将的值从大到小排序，其值越大表明该机位冲突越严重，可调整的余地越小；其值越小表明机位冲突越少。按照从难到易的顺序分别将子问题的解放到原问题中判断其是否可行，若可行则为原问题的一个解；反之则无解。假设通过拉格朗日问题得到的解y=(y1k，y2k，…，ynk)T不是机位分配问题的可行解，即存在i使得=0时，一个直观的可行化方法是：调整这些分配失败的航班的优先级，优先分配前一次规划失败的航班，在规划失败的航班中选取让λi为最小的k；令yik=1，并重复上述判别和计算直到所有的航班都被分配，这样可以将拉格朗日算法产生的所有解扩展至可行解。若上述方案最终还是无法得到可行解，则以再增加停机位个数来完成。

2.5 机场停机位分配调度优化算法

基于松弛算法的停机位分配调度优化算法具体步骤如下：

步骤1 初始化：令当前迭代次数u=0，令所有拉格朗日乘子λi=0。

步骤2 计算下界：用动态规划求解每个航班的子问题，得到原问题解的下界。

步骤3 解的可行化：对松弛问题的解进行可行化，得到原问题解的上界。

步骤4 更新解的上下界。

步骤5 判断是否满足终止条件：所得问题解的上界和下界差小于最优间隔或迭代次数大于200 时，则终止迭代，获得最终解［15］。

步骤6 更新拉格朗日乘子：设定迭代步长初始值为β=2，则令βu+1=0.8βu且u=u+1，根据2.3 节介绍的次梯度算法更新拉格朗日乘子λi，并跳转到步骤2（参考文献［15］对系数进行设定）。

3 实例分析

本文以某国际机场为研究对象，选用该机场5 月份某个繁忙日8：00—12：00 的航班数据，在此时间段内共有56 架航班、38 个停机位，其中包括近机位34 个、远机位4 个。数据样本如表1所示。

3.1 预分配方案前后对比

从图1 所示的原计划机位分配甘特图可以看出，1 号和9号停机位中两航班间的空闲时间较少，当有航班延误时对后续航班占用机位的影响较大，分配方案的鲁棒性较差。与原分配方案相比，如图2 所示的优化后机位分配图，其航班间的空闲时间分布均匀且间隔较大，能较好地吸收一定时间范围内航班延误产生的扰动，减少航班延误对分配方案的影响。

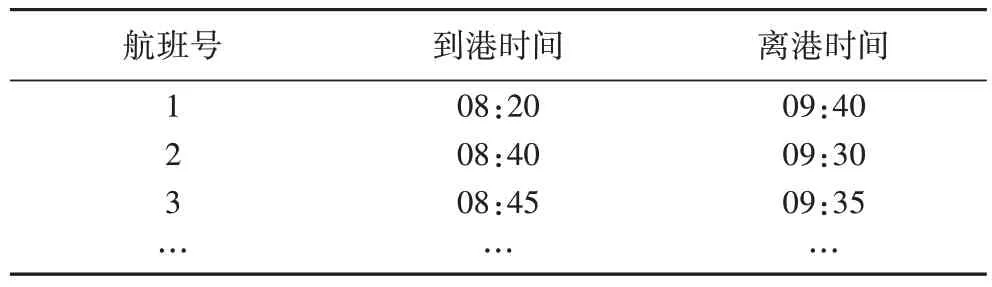
表1 部分航班计划Tab.1 Part of planning flight schedules

图2 优化后的停机位预分配甘特图Fig.2 Gantt Chart of gate pre-assignment after optimization

式（20）和（21）分别为机位空闲时间及机位占用比的计算方法：

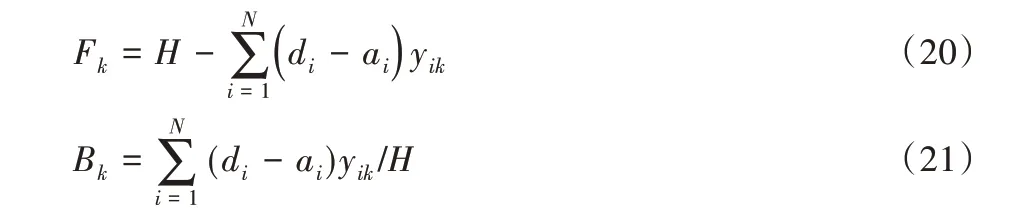
其中：Fk为第k个机位的空闲时间；H为机位总时间；Bk为第k个机位的占用比。

3.2 机位空闲时间对比

优化前后的机位空闲时间如图3所示。从图3中可知，优化前机位最大空闲时间为270 min，最小空闲时间为140 min，求得其平均空闲时间约为220.9 min；优化后的平均空闲时间为204.2 min，空闲时间缩短了7.56%，满足了目标函数中缩小机位间的空闲时间的需求，验证了本文所提方法的有效性。

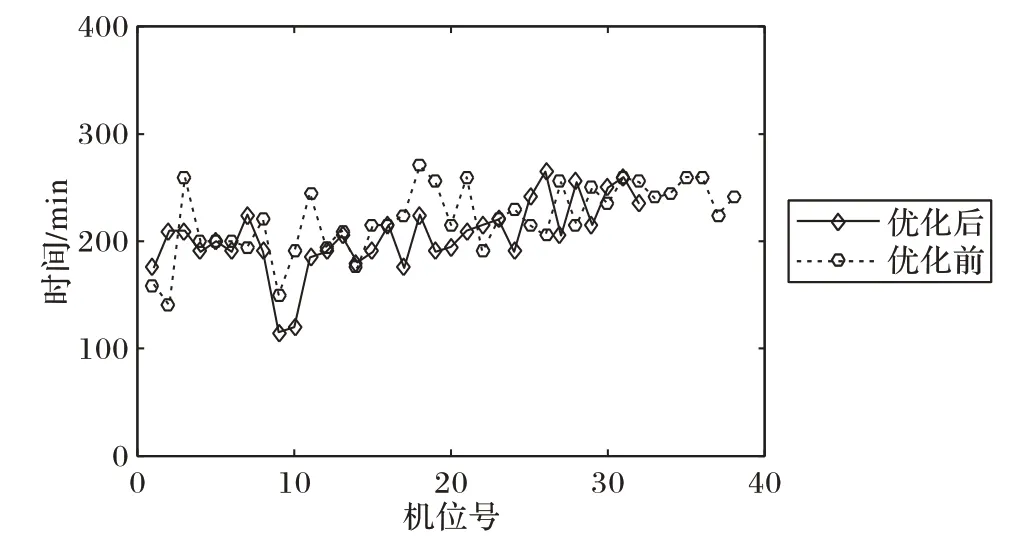
图3 优化前后的机位空闲时间Fig.3 Gate idle time before and after optimization

3.3 机位占用比对比

从图4 可以看出，优化后的机位预分配方案中几乎大部分机位的占用比均有所提高，平均占用比为34.12%，而优化前的平均占用比只有28.74%，增幅为18.72%。大大提高了机位的利用率。

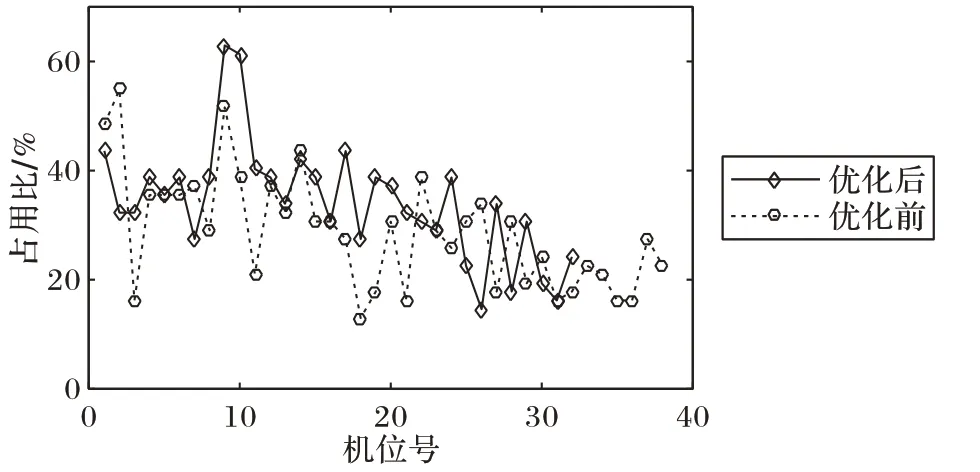
图4 优化前后机位占用比（8：00—12：00）Fig.4 Gate occupancy ratio before and after optimization（8：00 to 12：00）

根据调查，该枢纽机场的航班高峰时段分别为8：00—12：00和15：00—18：00，同理采用上述方法对15：00—18：00 的39 个航班进行分配，得到机位占用比如图5 所示。从图5 中可以看出，优化后使用停机位的数量从30 个减少到26 个，停机位占用比从22.84%提高到26.36%。综上可知，本文提出的基于松弛算法的停机位分配方法可以适应不同航班延误时间、不同航班密度等情况。

图5 优化前后机位占用比（15：00—18：00）Fig.5 Gate occupancy ratio before and after optimization（15：00 to 18：00）

表2 部分航班实际到离港时刻Tab.2 Arrival and departure time of some real flights

3.4 实际运行对比

将当日航班实际到、离港时刻运用到预分配方案中，表3为实际运行数据。这56 个航班中，航班最早到达时刻为8：22，航班最晚离港时刻为19：00。与原分配方案相比，优化后分配方案所用停机位数量从38个缩减到32个，机位使用量减少了15.79%，并且所有航班都被分配在近机位上，符合优化目标中最小化远机位占用时间的要求，这样既方便旅客上下飞机，又减少了调用摆渡车等的使用费用。

表3 实际运行数据Tab.3 Actual operation data

从表3 中可以看出，实际运行中，优化后的占用比相较优化前提高了22.47%，原冲突率为5.36%，优化后冲突率为3.57%，所以总的来说优化后的方案整体性能较好，达到了提高机位占用比、减少航班冲突的效果。

4 结语

本文研究了停机位分配问题，以提高停机位利用率为目标，并提出基于松弛算法的停机位分配模型求解方法，具体包括如下几个方面：1）通过对机场的停机位分配业务流程进行深入分析，基于机场航班实际运行需求，构建了停机位分配模型。2）使用拉格朗日松弛算法对模型进行求解，得到一个停机位预分配方案。3）将实际运行数据运用到预分配方案中并与原方案进行对比，结果分析表明，所提方法得到的结果使得机位利用率提高，冲突率降低，在实际运行中是可行的。

停机位分配是一个动态调整的过程，其分配方案的影响因素也十分复杂，包括航班延误、不同天气条件等影响，接下来下将针对实时动态调整停机位分配的问题进行近一步研究。