面向不均衡数据集的过抽样算法

崔 鑫，徐 华，宿 晨

（江南大学物联网工程学院，江苏无锡 214122）

（∗通信作者电子邮箱1525754926@qq.com）

0 引言

不均衡数据，即各类别样本数量分布严重不平衡的数据。对于均衡数据，传统分类算法可以取得良好的分类效果，但在实际问题中，如人脸年龄估计、异常检测、软件缺陷预测、图像标注等，需要分类的数据通常是不均衡的。而传统分类方法用以解决不均衡数据分类问题，往往在少数类上的分类效果并不能让人满意。这是由于不均衡数据中少数类数量过少，导致数据集并没有包含足够的分类信息。此外传统分类方法追求整体的正确率最大化导致分类结果更倾向于多数类，而可能误分类人们更关注的少数类。所以针对不均衡分类问题，学术界有必要去寻找一种行之有效的算法。

对于不均衡数据分类问题有一系列方法陆续被提出，这些方法可以分为算法层面和数据层面。算法层面包括代价敏感［1］、特征选择［2］和集成学习方法。在不均衡分类问题中人们通常更关注少数类，因此少数类才是不均衡分类的关键。针对不均衡数据中样本重要性不同的特点，代价敏感学习给予各类别不同的错分代价。例如在二分类问题中给予少数类更高的错分代价，迫使分类器对少数类取得较好的识别效果。特征选择方法在用于不均衡分类问题同样取得较好的效果。如果数据集中不同类别样本分布不均衡，则特征分布也可能会不均衡。因此选取最具有区分度的特征不仅可以降低复杂度，还有助于提高少数类的识别精度。集成学习即组合多个弱分类器得到一个强分器，由于其独立性，集成学习常与抽样方法、特征选择方法相结合，例如：Guo等［3］提出了集成学习方法BAK（BPSO-Adaboost-KNN），该算法将基于简化粒子群优化（Simple Particle Swarm Optimization，BPSO）的特征选择方法与Adaboost相结合；Liu 等［4］提出了集成算法GU-MOACOFS（Genetic Under-sampling and MultiObjectiveAnt Colony Optimization based Feature Selection），该算法更是同时使用了欠抽样、特征选择和集成方法。

数据层面的方法是采用重抽样方法均衡数据集中样本分布，重抽样分为过抽样和欠抽样。例如较为简单的过抽样方法是随机过抽样（Random OverSampling，ROS），该算法随机复制少数类样本以增加少数类样本的数量。由于该算法实现简单且性能良好，随机过抽样算法经常在研究中被用作基准算法进行比较。Ha 等［5］提出了基于遗传算法的欠抽样（Genetic Algorithm based Under-Sampling，GAUS），通过对损失函数寻找最优解得到最佳数据子集。与遗传算法一样，聚类算法也被用于提高抽样算法的性能，例如：Rayhan 等［6］提出的欠抽样算法（Clustering based Under-Sampling approach with BOOSTing algorithm，CUSBOOST），该算法在聚类所得簇中随机选择部分样本；Lin 等［7］提出了两种基于聚类的欠抽样方法，则直接使用簇心或最接近簇心的样本来代替原数据。过抽样和欠抽样虽然可以平衡数据分布，但欠抽样可能会删除对分类有价值的数据，过抽样则会增加过拟合的风险而且可能引入不合理的样本数据。针对过抽样会引起过拟合的缺点，Chawla 等［8］提出了合成少数类过抽样技术（Synthetic Minority Over-sampling TEchnique，SMOTE）算法，其思想是用少数类与其近邻的少数类合成新样本；但噪声样本可能参与合成新样本，模糊多数类和少数类间的边界。

针对上述SMOTE 的不足，许多研究人员提出了SMOTE的改进算法［9-11］。Bastista 等［12］提出了将SMOTE 算法和数据清洗方法相结合的方法SMOTE+ENN（Edited Nearest Neighbor）和SMOTE+Tomek links，在一定程度上保证了多数类和少数类的可分性。Han 等［13］提出Borderline-SMOTE 算法，该算法只对边界附近的少数类进行抽样。袁铭［14］提出了R-SMOTE 算法，在2个少数类样本上使用N维球体，使生成的样本在分布球体之内。R-SMOTE 算法消除了生成少数类实例分布的限制，提高了少数类的分类精度。赵清华等［15］提出了最远点算法（Max Distance SMOTE，MDSMOTE），摒弃了传统SMOTE 算法将正类样本点分组的思想，只关注少数类样本质心点和距离样本质心点最远距离的样本点。

以上算法的性能与SMOTE 算法相比得到了一定程度的提高，但总体分类性能还是稍显不足。为了进一步提高SMOTE 算法的性能，避免噪声样本参与合成样本，提高新样本的合理性，本文结合聚类算法提出了SMOTE 的改进算法

CSMOTE （Clustered Synthetic Minority Over-sampling TEchnique）。CSMOTE算法抛弃SMOTE在最近邻间线性插值合成样本的思想，使用少数类的簇心与其对应簇中样本进行线性插值合成样本，并根据簇心和样本间的欧氏距离只选用了部分样本。由于对参与合成的样本进行了筛选，所以可以一定程度避免使用噪声数据合成新样本，同时保证多数类与少数类间边界的明确性。最后在多个实际数据上，与四个SMOTE 的改进算法以及两种欠采样方法相比较，CSMOTE 算法具有更好的分类效果，说明该算法可以有效解决不均衡数据分类问题。

1 CSMOTE算法

1.1 CSMOTE算法设计思想

在不均衡数据集中，SMOTE 算法虽然可以平衡类分布，却可能会模糊多数类和少数类的边界。如图1（a）所示。假设SMOTE 对图1（a）中的少数类A 进行过抽样，在样本A 的最近邻中随机选择一个样本，假设选择了样本B，样本A 和B 的线性插值可以合成样本C。样本C 因为侵占多数类的样本空间，所以合成的样本C 是一个不合理的样本数据。在这种情况下，合成的样本C并不会有助于分类器的训练，反而由于样本C 的存在会使得数据变得更加难以区分，同时会影响分类器的性能，所以保证新样本的合理性是十分有必要的。

针对上述问题，本文提出了CSMOTE算法，该算法在少数类数据集的各个簇的范围内合成新样本。CSMOTE 算法的基本思想是对于簇中的一个少数类样本minority，计算minority与其对应簇的中心点center的欧氏距离dis，如果不存在某个多数类样本majority与center的距离d小于dis，则使用minority和center进行线性插值生成新的少数类样本，否则放弃使用样本minority。如图1（b）所示，在少数类集合上使用k-means 算法得到了簇A 和B。图中圆形表示多数类，矩形表示少数类，星型代表簇的中心点。在簇A中，由于多数类样本D 与簇A 中心点的距离小于簇A 中所有少数类样本与簇A 中心点的距离，所以CSMOTE 放弃在簇A 的范围内合成新的样本数据。簇B 中心点与最近的多数类样本的距离大于簇B 中心点与簇中少数类样本的距离，所以簇B 中的少数类均可参与新样本的合成。综上所述，CSMOTE 在簇B 中使用簇中心点和少数类样本合成新样本，且放弃了在簇A中合成新样本，从而避免了合成的样本点落入多数类的样本空间，保证了新样本的合理性。此外，CSMOTE 将簇的中心点加入到少数类数据集中，这可以丰富数据集中少数类的样本分布。

1.2 CSMOTE算法流程

CSMOTE 算法流程如图2 所示，首先将不均衡数据集分为少数类和多数类，在少数类上使用k-means聚类获得多个子簇。依次在每个子簇中进行过抽样，在子簇中随机选择参与合成的样本，并根据所选样本与对应簇心的欧氏距离判断其是否可以参与合成。然后将簇心与所选样本进行线性插值获得新样本。最后将合成的新样本、簇心以及原少数类样本与多数类相结合获得均衡的数据集，将均衡数据集作为训练集用于训练分类器。算法具体步骤如下所示：

输入 多数类集合maj={x1，x2，…，xm}，少数类集合min={x1，x2，…，xn}，聚类的个数k，过抽样的倍数Rate，重复选择的次数T。

输出 合成的少数类集合newMin。

1）首先对少数类集合使用k-means 聚类，生成k个簇{C1，C2，…，Ck}，其对应的聚类中心为{u1，u2，…，uk}，初始化newMin={u1，u2，…，uk}。

2）如果所有的簇都已遍历，则转到步骤6），否则依次遍历簇集合{C1，C2，…，Ck}取得簇Ci。

3）在簇Ci中随机选择一个样本xj，如果isUse(xj)==True，转到步骤4）；否则重新选择样本xj，如果重新选择T次均没有选择到样本满足isUse(xj)==True，则转到步骤5）。

4）生成一个0到1之间的随机数Rate，利用簇Ci中心点ui和xj合成一个新样本xnew：

5）重复步骤3)Rate*|Ci|次，然后转到步骤2）。

6）输出合成的少数类newMin。

isUse(xj)：

a）计算xj和聚类中心点ui的欧氏距离dis。

b）遍历maj集合中样本xt，计算xt和聚类中心点ui的欧氏距离d。如果存在xt使得d＜dis，则返回False；否则返回True。

CSMOTE 算法中的子步骤isUse(xj)是用于判断选中的样本xj是否可以参与合成新样本。步骤1）对少数类集合进行kmeans聚类获得k个簇，并将所有的簇心加入到合成的少数类集合。步骤2）对簇集合进行遍历，步骤3）在当前簇中随机选择样本，并用子步骤isUse(xj)来判断该样本是否可以参与合成，如果不满足条件则重新选取；否则跳转步骤4）使用选中的样本和对应的簇心合成新样本并加入到合成的少数类集合。步骤5）控制合成的样本数量，每个簇合成的样本数量为对应簇中样本数量的Rate倍。步骤6）输出合成的少数类集合。

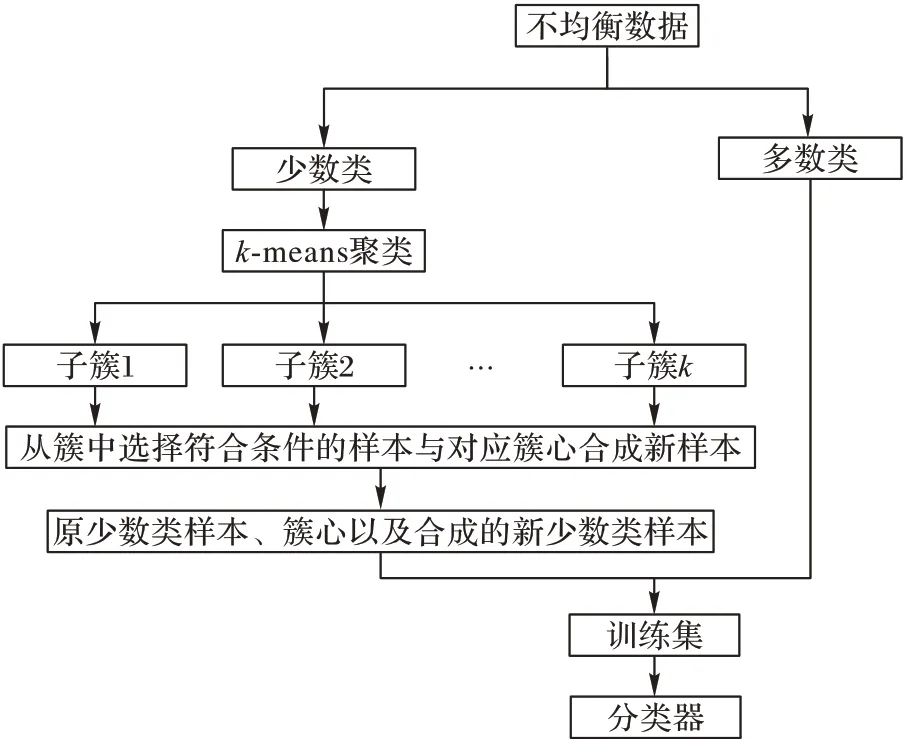
图2 CSMOTE算法流程Fig.2 Flowchart of CSMOTE algorithm

1.3 CSMOTE算法复杂度分析

定义n为少数类样本数量，m为多数类样本数量，样本属性个数为b。子步骤isUse(xj) 的时间复杂度为O(m)。CSMOTE 算法流程中，步骤1）中，对少数类集合使用k-means聚类的时间复杂度为O(bfkn)，其中，f为迭代次数，k为k-means 算法的分类数，由于f和k一般远小于n，所以k-means算法的时间复杂度可简化为O(n)。在步骤2）到步骤5）中，算法的时间复杂度为O(kn(Tm+d))，T为重复选择的次数，本文中将其设为当前簇的样本数，所以时间复杂度为O(kn(nm+d))=O(n2m)。综上，CSMOTE算法时间复杂度为O(n2m)。

CSMOTE 算法空间复杂度取决于子步骤isUse(xj)中存储簇心与所有多数类样本的距离，因此，CSMOTE 算法空间复杂度为O(kn(nm+d))=O(n2m)。CSMOTE 算法的时间和空间复杂度均高于SMOTE 算法，可知CSMOTE 通过牺牲时间和空间上的效率获得了分类性能的提高。

2 实验与结果分析

2.1 数据集和评价指标

本文实验选用了六个数据集分别为pimax、german3、horseM、breastM、ilpdM、transfusionM。这六个数据集源于不同的实际应用领域，数据集的详细信息见表1，其中样本比率表示多数类与少数类的数目之比，数值越大表明该数据集的不均衡程度越大。在实验中曾尝试在输入数据时采用归一化处理，但是与未采用归一化处理相比较，除了在transfusionM 数据集上分类性能略有提升之外，其他数据集上所得分类性能均有较为严重的下降。此外，尝试在子步骤isUse(xj)计算欧氏距离时采用归一化处理，分类性能却略有下降。基于分类性能以及复杂度的考虑，实验中将不再对数据进行归一化处理。

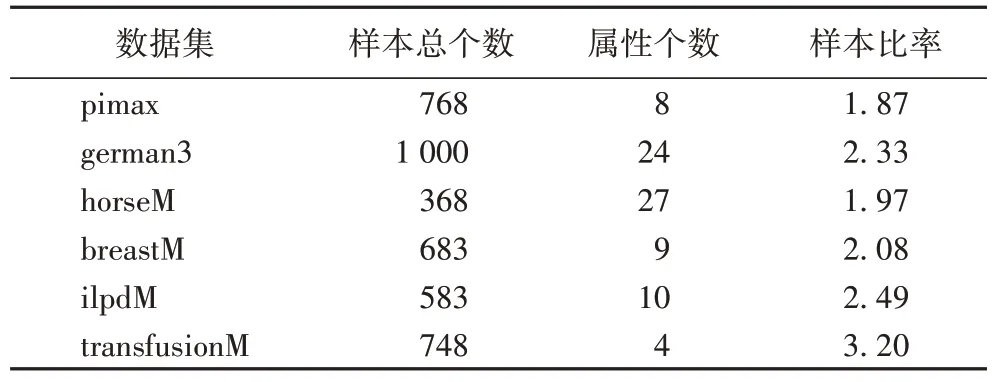
表1 数据集详细信息Tab.1 Details of datasets

在不均衡分类分类器的评估中，因为分类精度无法反映少数类的分类效果，所以分类精度将不再适用。为此，研究人员提出了许多基于混淆矩阵的评价指标，例如recall、sensitivity、F-measure 以及GM（Geometric Mean prediction accuracy）。混淆矩阵如表2 所示，少数类为正类，多数类为负类，列表示预测类别，而行表示真实类别。

表2 混淆矩阵Tab.2 Confusion matrix

TP表示正类样本被正确分类的数量，TN表示负类样本被正确分类的数量；FN表示正类样本被错误分类为负类的数量，FP表示负类样本被错误分类为正类的数量。本文实验采用接受者操作特性曲线（Receiver Operating Characteristic curve，ROC）下的面积（Area Under the Curve，AUC）［16］来定量比较不同分类模型的性能，越大的AUC 代表分类的效果越好，AUC 为1 表示达到了最理想的分类效果，而AUC 为0.5 表示是随机猜测。AUC的计算式如下：

式中：TPrate表示少数类中被正确分类的比率，其取值范围为［0，1］；FPrate表示多数类中被错误分类的比率，其取值范围为［0，1］。TPrate、FPrate计算式如下：

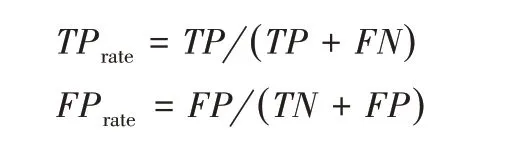
2.2 实验步骤

图3 展示了实验流程，实验流程描述如下：给定一个二分类的不均衡数据集，第一步基于K折交叉验证将数据集分为训练集和测试集。第二步将训练集分为多数类子集和和少数类子集，然后使用过抽样方法增加少数类子集中样本数量，将过抽样后的少数类子集和多数类子集相结合获得均衡数据集。最后，分类器在均衡的训练集和测试集分别进行训练和测试。

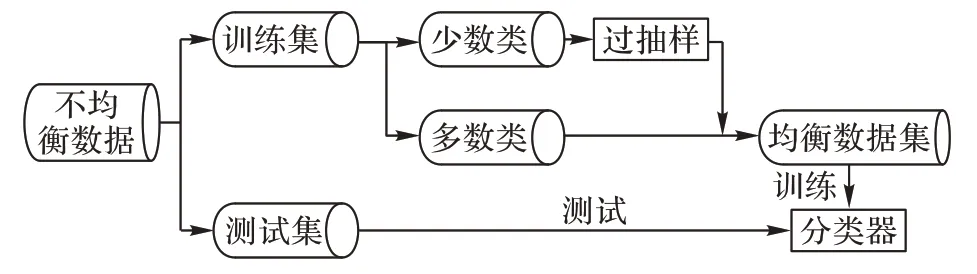
图3 实验流程Fig.3 Flowchart of experiment

2.3 CSMOTE算法聚类参数k的确定

聚类参数k会影响合成少数类的分布情况，所以参数k的确定对CSMOTE 算法的性能十分重要。因此本文将选择1、3、5、7、9、11 这6个1～11 之间的奇数作为k的值，通过对比CSMOTE 算法在不同参数k下过采样后分类器所得的AUC 值来确定最佳的k值。不同k值的CSMOTE 算法在pimax、german3、horseM、breastM、ilpdM、transfusionM 数据集上的分类结果如图4所示。

由图4 可以看出，在german3、ilpdM 和transfusionM 数据集上CSMOTE 在k=7 时获得了最大的AUC 值。而在pimax、horseM 和breastM 数据集上，k=7 时CSMOTE 虽然并未取得最优的AUC，但是与最优的AUC 值相比差距较小。其中在horseM 数据集上k=9 时取得最优值0.926，k=7 时则取得了仅次于最优的AUC 值0.925 8，k=7 时AUC 值仅比最优值低了0.000 2。在pimax 数据集，k=3 时取得最优值0.820 5，k=7 时取得的AUC 值为0.819，k=7 时AUC 值仅比最优值低了0.001 5。在breastM 数据集，k=3 和k=9 时取得最优值0.994 8，k=7 时取得的AUC 值为0.994 2，k=7 时AUC 值仅比最优值低了0.000 6。从六个数据集的均值来看，CSMOTE 在k=1，3，5，7，9，11 时获得的平均AUC 值分别为0.822 5、0.823 8、0.824 0、0.828 5、0.823 0、0.821 7，k=7 时AUC 值比k=1，3，5，9，11 时分别高出0.006、0.004 7、0.004 5、0.005 5、0.006 8，由此可知k=7 与其他k值相比具有一定优势。综上所述，在下文的实验中CSMOTE 的聚类个数k选择为7。聚类参数k取决于数据集自身的特点，即样本的分布情况。由于本文选用的数据集均为不均衡数据集，少数类可能被多数类分割为多个子区域，所以经过实验确定的聚类参数k较大为7。除了通过多次实验确定k值之外，在实际应用中确定k值的方法有：1）数据可视化，通过观察数据的聚合程度确定参数k；2）手肘法；3）轮廓系数法。

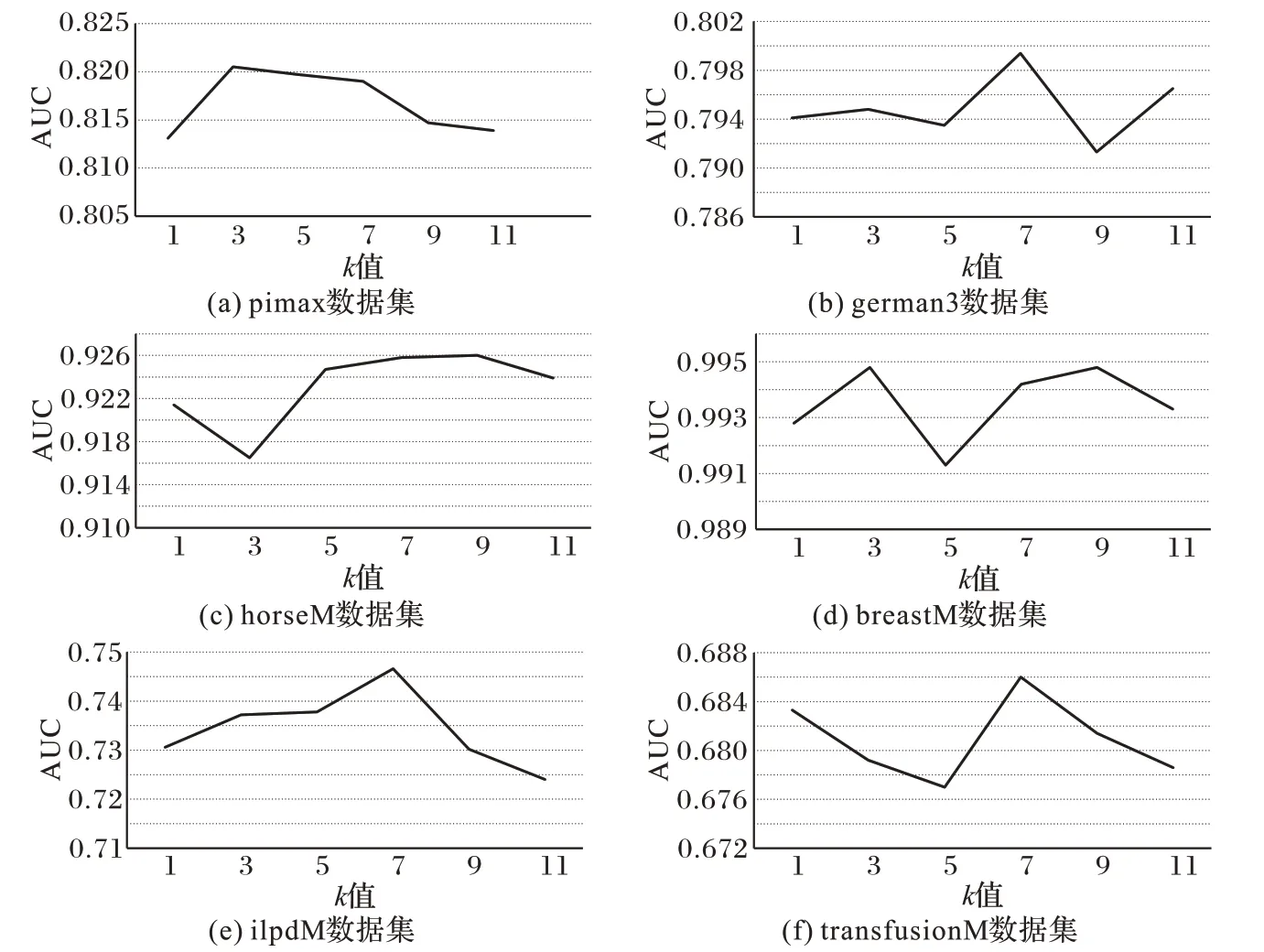
图4 不同k值的分类效果Fig.4 Classification effects of different k values on different datasets

2.4 不同算法的性能比较

为了进一步研究CSMOTE 算法的性能，在六个数据集上将CSMOTE 与Borderline-SMOTE、R-SMOTE、MDSMOTE、improvedSMOTE［17］和文献［7］所提出的两种欠抽样方法（分别简记为UC和UCN）进行比较。除了transfusionM 数据集之外，实验所采用的数据集的不均衡比均为2 左右，且考虑到CSMOTE 算法选择参与合成样本的条件过于苛刻，如果过抽样的倍数Rate设置过大可能会产生冗余样本降低算法的效率，所以过抽样的倍数Rate设置为1。CSMOTE在簇中随机选择参与合成新样本，但是难以保证一次就选到符合条件的样本，为了合成足够的新样本，同时考虑到时间成本，文中实验将重复选择的次数T设置为当前簇中样本个数。CSMOTE 聚类参数为2.3节调优所得k=7，实验所采用的分类器是以决策树为基分类器的bagging。实验中为保证结果的准确性，采用十折交叉验证法，将数据集平均分为10 份，然后依次选择其中1 份作为测试集，其余9 份作为训练集，该过程重复10 次。实验结果如图5 所示，不同算法在6 个数据集上AUC 的均值如表3所示。

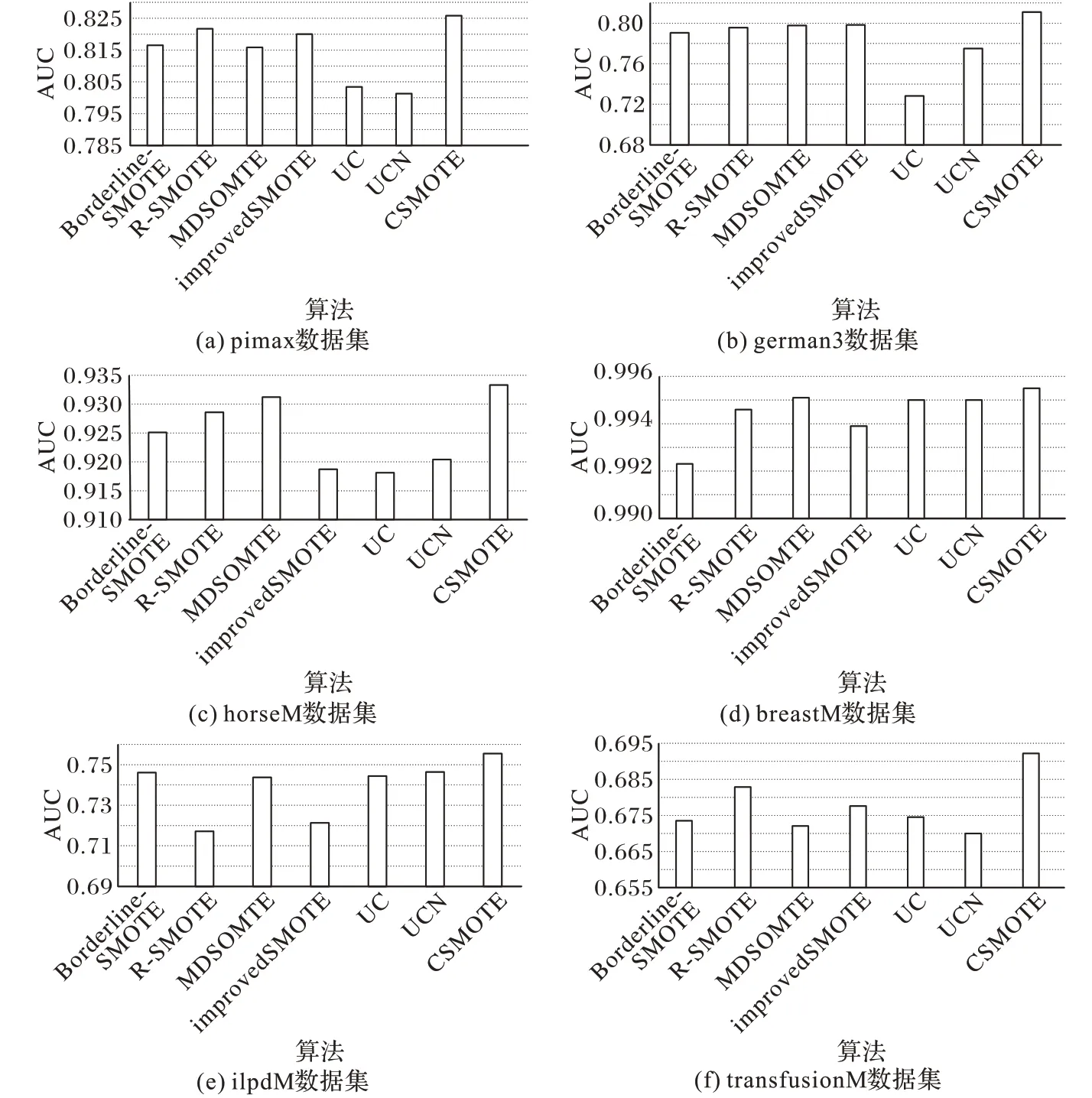
图5 不同数据集上七种算法分类性能对比Fig.5 Classification performance comparison of seven algorithms on different datasets

表3 七种算法的分类效果（AUC）对比Tab.3 Classification effect（AUC）comparison of seven algorithms

从图5和表3可以看出，在所有数据集上CSMOTE均取得了比其他算法更高的AUC，说明CSMOTE 的分类效果更好。其中，在german3 数据集上CSMOTE 的优势最为明显，可以比其他算法平均高出0.030 1。在pimax、horseM、ilpdM 和transfusionM 数据集上，CSMOTE 可以比其他算法平均高出约0.013 6。从均值来看，CSMOTE 依然具有优势，CSMOTE 比Borderline-SMOTE、R-SMOTE、MDSMOTE、improvedSMOTE、UC 和UCN 分别高出了0.011 6、0.012 1、0.009 6、0.013 9、0.025 0、0.017 5。在horseM 数据集上所有算法均取得了0.9以上的AUC，在数据集breastM 上更是达到了0.99 以上的AUC，这表明所有算法在这两个数据集上均取得了较可靠的效果。

CSMOTE 算法与对比算法相比：1）避免了噪声数据样本参与合成新样本；2）利用簇心和样本间的欧氏距离实现了对少数类的区别对待；3）根据样本间的距离只选用了部分少数类参与合成新样本，所以新样本不会模糊多数类与少数类的边界。综上所述，通过了一系列的实验验证表明，针对不均衡数据分类问题，提出的CSMOTE算法是有效的。

3 结语

针对不均衡数据分类问题，本文从数据层面的方法出发提出了CSMOTE 算法。在实际数据集上，CSMOTE 与四个SMOTE 的改进算法以及两种欠抽样算法的分类性能进行了比较，结果表明CSMOTE 算法在处理不均衡数据集时具有更好的分类效果。该算法解决了已有算法中的不足，利用簇心和样本间的欧氏距离选择部分少数类样本参与合成新样本，既避免了噪声数据样本参与合成新样本，又解决了SMOTE 算法模糊多数类与少数类间边界的问题，从而提高了不均衡数据的整体分类性能。由于CSMOTE选择少数类样本参与合成样本过程的条件较为苛刻，所以对于某些数据分布，参与合成的少数类数量过少导致合成的样本分布过于集中。故下一阶段研究工作就是解决CSMOTE在某些数据集中合成的新样本分布过于集中的问题。