多传感器系统中的小波变换应用研究

汤家森 李瑞祥 施伟斌 李辉

摘要：针对惯性传感器测量系统中采用单一传感器往往会因测量噪声及误差而降低系统检测精度等问题，根据传感器分辨率各不相同的特性，结合小波多分辨率分析的特点，采用Mallat快速算法并在各尺度上应用卡尔曼滤波处理，实现对不同传感器观测数据的融合。设计算法进行仿真实验，结果证明，算法有效提升了融合数据信噪比（SNR），得到不失真的融合信号波形，提高了惯性传感器系统精度。该算法相比对惯性传感器数据进行简单滤波处理再进行特征选取的普遍做法，应用在多传感器的人体姿态识别系统中可以降低数据处理复杂度，证明了利用小波变换对惯性传感器数据去噪融合的实用性。

关键词：传感器系统;小波变换;数据融合;姿态识别

DOI： 10. 11907/rjdk.191781

开放科学（资源服务）标识码（OSID）：

中图分类号：TP319

文献标识码：A

文章编号：1672-7800（2020）004-0199-04

0 引言

人体姿态识别研究中常采用惯性传感器如加速度计陀螺仪获取实时运动信号[1-2]，这类传感器在体积、重量和测量精度等各方面的优点使其得以广泛应用，单传感器系统测量结果往往伴随很多随机噪声，而将多种分辨率不一的传感器信号加以滤波及融合以提升系统测量精度，需要利用合适的方法。文献[3]提供的自适应加权融合算法将动态系统中不同传感器数据进行加权融合，算法较为直观但精度不佳;文献[4]对小波滤波后的数据采用提升小波变换，实现不同带宽信号融合，融合结果幅值衰减小于-2.5DB;文献[5]采用A-trous快速小波变换对滤波后的两组仿真信号进行融合，将不同分辨的信号转换成相同分辨率，证明了小波分析对传感器数据融合的有效性。小波变换在时频域均有良好的分辨性，在不同尺度下具有不同的局部特征。因此，小波提供了良好的信号处理方法，可以应用于惯性传感器系统。

本文利用小波分析的特有属性建立对多传感器融合的信号分析方法，通过比较相似度确定合适的小波基函数，并利用快速Mallat算法实现惯性传感器加速度计陀螺仪信号中的噪声抑制，以更好地分析惯性传感器系统的特征和规律。

1 惯性传感器系统信号小波去噪原理

1.1 小波函数基本特点

小波变换一方面继承于傅立叶变换局部化的思想，另一方面克服了傅里叶变换频率分析等缺点，可以作为对信号时频分析处理的理想工具。其主要特点是通过变换能够突出特征，也能实现对时间频率的局部化分析，通过伸缩平移运算对信号进行多尺度细化，能自动适应时频信号分析要求。

函数厂（t）对于给定小波基函数的连续小波变换为：

由式（1）可以看出，相比于只有一个频率变量的傅里叶变换，小波变换有两个变量：尺度a和平移量r。尺度a直接影响小波函数伸缩，不同尺度因子生成不同的频率成分;平移量r直接影响小波函数的平移，使得小波能够沿信号的时间轴实现遍历。

小波重建如式（2）。

考虑到实际传感器固有的采样频率，本文采用小波变换的离散形式。

1.2 小波基函数选取

对信号作小波变换处理，寻找适当的小波基函数作为母函数尤其重要。常见的小波基函数包括Db小波、Bior-thogonal小波、Coiflet小波、SvmletsA小波、Morlet小波、Mexican Hat小波、Meyer小波等[6]。

由式（1）可以看出，小波变换表达为信号和小波基函数的卷积。因此在小波变换过程中.原信号波形和小波基函数相近的特征会被放大，而不同特征的信号则被抑制。选取与原信号相似度高的小波基函数，有利于对特征信号的提取。因此，相似度也可以用来作为衡量小波变换效果的一种评价标准[7]。

小波基函数和原信号的相似度如式（3）。

DB5小波函数与行走状态下加速度计信号对比如图2所示。

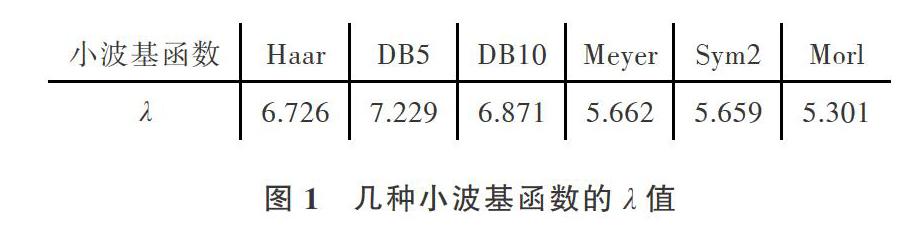
由图1、图2可知，DB5小波和惯性传感器采集到的运动信号相比，有较高的相似性，具有正交性。DB N（N=1，2，3，…，10）系列小波函数长度为2N-1，率波长度为2N，消失矩为N。其中，对本实验数据DB5的相似度要优于Haar及DBlO，如果小波分解层数过多则导致失真，分解层数不够则不能有效滤噪。

2 惯性传感器系统描述

3 多尺度融合算法设计

3.1 小波变换多尺度分解

采用Mallat分解，与用快速傅里叶变换实现傅里叶变换类似，Mallat算法也可以实现快速小波变换，具体流程如图3所示。

3.2 卡尔曼滤波

卡尔曼滤波对非平稳信号有较强的估计能力，可对小波变换得来的低频信号与许多高频信号在各尺度上分别加以处理，得到更优估计。

综上，基于小波变换和卡尔曼滤波的多尺度融合算法基本思路为：①通过Mallat快速小波變换把Ⅳ个传感器的原信号分解在若干个尺度上;②在各尺度上分别用卡尔曼滤波处理;③将各尺度上的全局估计结果应用Mallat快速重构算法，得到融合信号[14]。

4 实验与评估

采用传感器MPU9250、STM32F103单片机和电源灯硬件组成系统，采集人在行走过程中的加速度信息和角速度信息，验证信息融合的有效性，系统架构如图4所示。操作流程为开机后初始化MPU9250，然后在死循环里读取加速度传感器、陀螺仪等数据，将数据通过I2C总线协议传到单片机，单片机再将数据上传到上位机并储存串口上报给上位机，利用上位机软件实时显示传感器状态曲线。

用计算机算法仿真时，选择与原信号相似度较高的具有良好正交性与双正交性效应的DB5小波分析模拟信号，作5层分解，卡尔曼滤波处理后再小波重构，仿真结果如图5所示。其中，原始信号信噪比分别为9.5dB、8.6dB，融合结果为16.8dB。

对比图5（c）和图5（a）、图5（b）可知，对于非平稳信号去噪，小波变换结合卡尔曼滤波的消噪效果明显，保留了原始信号特征。图5（d）采用DB3小波作为小波基函数，作三层分解，算法融合结果出现图示两处失真，证明准确判断小波基函数及分解层数的影响意义。该方法可应用于人体姿态识别系统的测量数据处理上，鲁棒性良好。

5 结语

获取准确的传感器数据对人体姿态识别研究具有重要意义。本文基于传感器MPU9250采集到的加速度、角速度信息，构造与原信号相似度较高的小波基函数，根据小波分析多分辨率的特点，利用快速小波变换对多传感器信号进行多尺度分解重构，并在各尺度上对信号进行滤波处理。实验效果滤除了传感器运动过程中的随机噪声并突出信号特征，能更直观地观测信号，提高了惯性系统准确性。对传感器高低频率范围的适应性以及对处理后数据的特征提取是下一步研究重点。

参考文献：

[1]

CHOU K C，GOLDEN S A， WILLS KYAS. Multiresolution stochasticmodels. data fusion， and wavelet transform [Jl. Signal Processing，1993，34（3）：257-282.

[2]

SEOKHOON K. ANAND P， CWANGGIL J. Reduction of mixed noisefrom wearable sensors in human-motion estimation [J]. Computersand Electrical Engineering， 2017（ 61）： 287-296.

[3]李媛媛，张立峰，多传感器自适应加权融合算法及其应用研究[J].自动化与仪器仪表，2008（2）：10-13.

[4]蒋行国，杨文淑，包启亮，等.基于小波变换的两种惯性传感器数据融合[J].光电工程，2007，34（1）：90-94.

[5] 刘素一，张海霞，基于A-trous小波变换的多传感器数据融合方法[J].软件导刊，2006（ 21）：89-90.

[6] 胡昌华.基于Matlab的系统分析与设计——小波变换[M].西安：西安电子科技大学出版社，2001.

[7] 陈泽鑫.小波基函数在故障诊断中的最佳选择[J].机械科学与技术，2005， 24（2）：172-175.

[8] 原琦，丁家满.海量信息融合方法及其在故障诊断中的应用[J].软件导刊2018， 17（8）：174-177.

[9]

LIANG Y H. XUE K. JIN H Z.Lift fin stabilizers based on data fu-sion with ，vavelet de-noising technology[J].Journal of Control Theoryand Applications， 2010.8（ 4）： 485-490.

[10]

LIGORIO G，ANCELO M，SABATINI.A novel Kalman fiher for hu-man motion tracking with an inertial-hased dvnamic inclinometer[J]. IEEE Trans. Biomed Eng.， 2015， 62（8）：2033-2043.

[11]

CORRALES J A， CANDELAS F A. TORRES F.Hybrid tracking ofhuman operators using IMU/UWB Data Fusion by a Kalman Filter[C]. Proceeding of 3rd ADM/IEEE International Conference on Hu-man-Robot Ineraction. 2008： 193-200.

[12]

ELMAR G.A high performance hvbrid electrical optical interconnec-tion technology for high speed electronic systems[J].IEEE Transac-tions on Advanced Packaging， 2001， 24（3）：375-383.

[13]

Preece S J，Coulermas J Y. Laurence P J K， et al.A comparison offeature extraction methods for the classification of dynamic activitiesfrom accelerometer data[J].IEEE Transactions on Biomedical Engi-neering， 2009， 56（3）：871-879.

[14] 劉素一，张海霞，罗维平.基于小波变换和Kalman滤波的多传感器数据融合[J].微计算机信息，2006，22（ 16）：179-181.

[15] 邓自立，祁荣宾.多传感器信息融合次优稳态Kalman滤波器[J].科技快报，2000.6（2）：183-184.

[16]陈亚峰，王直杰.基于MPU6050加速度信号的匹配小波设计及去噪[J].电子设计工程，2017.25（6）：114-117.

[17] 崔锦泰.小波分析导论[M].程正兴，译.西安：西安交通大学出版社.1995.

[18]冯智勇，曾瀚，张力，等.基于MPU6050加速度信号的匹配小波设计及去噪[J].西南师范大学学报，2011，36（ 4）：137-141.

[19]高嵩，潘泉，肖秦琨.多传感器自适应滤波融合算法[J].电子与信息学报，2008，30（8）：1901-1904.

[20] 李洪波，杨军锋.自适应Kalman滤波在多传感器数据融合中应用[J].国外电子测量技术，2006. 25（6）：69-71.

[21]蔡猛.基于小波变换的多传感器最优信息融合[J].电光与控制，2013，20（ 12）：97-100.

[22] 孙书利，邓自立.多传感器线性最小方差最优信息融合估计准则[J].科学技术工程，2004，4（5）：334-337.

（责任编辑：孙娟）

作者简介：汤家森（1992-），男，上海理工大学光电信息与计算机工程学院硕士研究生，研究方向为无线传感器网络;李瑞祥（1967-），男，硕士，上海理工大学光电信息与计算机工程学院工程师，研究方向为无线传感器网络;施伟斌（1967-），男，博士，上海理工大学光电信息与计算机工程学院副教授，研究方向为无线传感器网络;李辉（1996-），男，上海理工大学光电信息与计算机工程学院硕士研究生，研究方向为无线传感器网络。