基于检测器集层次聚类的否定选择算法
王韫烨,孔 珊
(郑州师范学院 信息科学与技术学院,郑州 450044)
0 概述
异常检测是在网络和大数据安全分析中广泛使用的关键技术。由于异常检测系统与人体免疫系统有着高度的相似性,基于免疫机制的否定选择算法在异常检测中得到了深入应用并取得良好的效果[1],成为解决异常检测问题的主要算法之一。检测器的生成是否定选择算法中的重点部分,对检测效率和准确度具有重要影响[2]。因此,设计高效的检测器生成算法是否定选择算法研究的关键和热点[3]。
否定选择算法一般用字符串(含二进制字符串)和实值表示[4]。实值否定选择算法将自体与检测器的各项属性值表示为n维[0,1]实数范围([0,1]n)内的超立方体,更适合对现实问题进行描述,因而得到广泛应用[5]。由于半径固定的实值否定选择算法存在许多黑洞区域无法被检测器覆盖和检测,文献[6]提出V-detector算法,该算法是一种半径可变的实值否定选择算法,可以显著提高算法的检测率,为实值否定选择算法中最具代表性的算法,众多后续研究与应用都基于该算法展开[7-16]。
文献[7]提出改进的否定选择算法,该算法增加了检测器的覆盖半径。文献[8]通过二次否定过程提高了检测器生成性能。文献[9]基于自体分布由远及近分层次产生检测器,优化了否定选择算法的性能。文献[10]在小型样本空间中分离自体与非自体空间,提高了检测器的检测效率。文献[11]通过分析抗原空间的密度,提升了实值否定选择算法的性能。文献[12]采用基于子空间密度搜索的改进否定选择算法提高了空间覆盖率。文献[13]对否定选择算法性能参数进行分析,指出各参数对检测性能的影响。文献[14]将主动学习和否定选择算法进行集成后应用于垃圾邮件分类,增加了垃圾邮件分类准确性。文献[15]将改进的否定选择算法用于故障检测,提升了检测率。文献[16]用否定选择算法生成测试数据,有效提高了测试数据路径覆盖率。
上述否定选择算法均取得了较好的效果,显著提高了检测器的生成效率。但采用否定选择算法对数据进行异常检测时,需要对所有的检测器进行距离计算,这降低了检测效率,增加了检测时间,不利于快速检测。
本文提出一种基于检测器集层次聚类的否定选择算法,对检测器集进行从上到下的层次聚类处理,只计算待检测数据与聚类中心检测器之间的距离,以减少计算时间和能耗,对未被检测器匹配的数据进行分类,并分别从检测率、误检率及检测时间等方面将本文否定选择算法与V-detector算法和免疫实值否定选择算法进行对比分析。
1 算法关键技术
1.1 否定选择算法的检测过程
否定选择算法的检测过程由两个阶段构成:一是训练阶段,即检测器的生成阶段;二是检测阶段,即将待测数据通过检测器按照是否正常进行分类的阶段[17]。
在检测阶段,待检测数据需要与检测器进行匹配,因此,需要匹配的检测器数量越少,对数据做出异常检测的判断就越快。
V-detector算法及其改进算法检测阶段的过程为[6-11]:对任一需要检测的数据,计算其与所有检测器的距离,若待检测数据被任一检测器覆盖,则该待检测数据被标记为异常,否则该待检测数据被标记为正常。对于n维空间中待检测数据t=(ct,rt)而言,将其与检测器d=(cd,rd)之间距离记为dis=(t,d),其中ct为待检测数据的中点,rt为待检测数据的半径,cd为检测器的中点,rd为检测器的半径。为判断待检测数据是否异常,需要计算各待检测数据ti(ti∈t)与所有的检测器di(di∈d)之间的距离,其计算公式如下:
dis(ct,cd)=
(1)
若dis(ct,cd) 由否定选择算法的检测过程可以看出,该过程计算会耗费较多的计算时间,这不利于该算法的广泛应用。 本文在上述否定选择算法的基础上进行改进,改进后算法的主要思想为:对检测器集D进行从上到下的层次聚类处理,只计算待检测数据t与聚类中心检测器C之间的距离,不再计算待检测数据t与所有聚类成员检测器集D之间的距离,减少了计算时间和能耗。 本文设计的检测器层次聚类过程为: 1)对否定选择过程生成的成熟检测器集D进行层次聚类处理,每层生成的聚类中心构成新的检测器集C。 2)对于每个检测集T中的数据t=(ct,rt),分别计算其与检测器集C中每个检测器Ci的距离,从而判断该待检测数据是否正常并进行分类。其中,ct为待检测数据的坐标,cc为检测器Ci的坐标,rci为检测器Ci的半径。具体的判断方法为:若dis(ct,cc) 在二维实值空间[0,1]2进行仿真验证如下: 由上述可见,层次聚类方法中聚类半径逐渐减半,从而使得检测更精确,在减少检测时间的同时提高了检测率。 在二维实值空间[0,1]2中,孔洞区是指没有被任何检测器覆盖的检测区域[18]。对于处于孔洞区的待检测(分类)数据,可以通过否定选择算法将其分类为正常数据。然而未被检测器覆盖的区域有可能存在异常数据并导致分类错误,造成算法误检率升高[19]。在改进后的否定选择算法中,不再将待检测数据简单标识为正常数据,其性质由检测器与自体集的位置共同定量决定,即待检测数据的异常性由该数据到最近检测器的欧氏距离和最近自体的欧氏距离共同判定,分别表示为: Dis1=min dis(t,ci),ci∈C (2) Dis2=min dis(t,si),si∈S (3) 其中,Dis1为待分类数据t到检测器集合C中所有检测器ci的最短距离,Dis2为待分类数据t到自体集合S中所有自体si的最短距离。若Dis1>aDis2,则该待检测数据为正常数据,否则为异常数据。大量实验研究结果表明,a的取值为自体半径rs的20倍[18]。 改进后否定选择算法的检验过程分为检测器生成阶段与异常检测阶段,该算法的基本步骤如下: 1)使用文献[6]中V-detector算法生成成熟检测器集D。 2)对检测器集D进行层次聚类处理,得到检测器集C。 3)输入数据集T进行异常检测(计算T中数据和检测器集C中检测器之间的距离。 4)进行异常检测判断:如果被检测数据与检测器集C中的任一检测器匹配,则为异常数据,直接进行第6步;如果被检测数据未与检测器集C中的任一检测器匹配,进行第5步。 5)如果被检测数据未与检测器集C中的任一检测器匹配,则认为其处于孔洞区,需进一步测试以判定其是否为正常数据并进行标识。 6)算法结束。 在Windows 10环境下,使用JAVA对本算法进行编程实现。实验数据集为广泛使用的人造二维数据集,对实验结果以五角星形自体集为例进行分析,并与经典的V-detector算法[6]和免疫实值否定选择算法[9]结果进行对比。参数取值与所对比的文献保持一致:数据取自二维实值空间[0,1]2,训练数据集容量为1 000个,测试数据集容量为1 000个,目标覆盖率分别为90%、95%和99%。分别从检测率、误检率及检测时间三方面对实验结果进行分析。 选择实验目标覆盖率为95%,自体半径的取值区间为[0.01,0.30](每隔0.05取一个值),每个自体半径进行100次实验并取结果的平均值。 由图1可以看出,3种不同算法的检测率均随着自体半径的增大而降低,本文否定选择算法的检测率降幅比其他两种算法更小。这是因为孔洞区数据随着自体半径的增大而增加,本文否定选择算法由于对孔洞区数据的异常性进行了判定,提高了孔洞区数据检测的准确性,从而提升了算法的检测率。 图1 检测率随自体半径变化曲线 由图2可以看出,3种不同算法的误检率均随着自体半径的增大而降低,本文否定选择算法误检率的降幅比其他两种算法的更大。这是因为孔洞区数据随着自体半径的增大而增加,在V-detector算法和免疫实值否定选择算法中,孔洞区数据(部分数据可能为异常数据)全部被定义为正常数据,而本文否定选择算法对孔洞区数据异常性进行了判定,有效降低了算法的误检率。 图2 误检率随自体半径变化曲线 由图1和图2可知,检测性能与自体半径密切相关,随着自体半径的增大,算法的检测率和误检率均降低。因此,需根据实际问题选择适合的自体半径来调整算法的检测性能。 由图3和图4可以看出,当自体半径为0.2时,3种算法的检测率和误检率均随着目标覆盖率的增大而增加;和其他两种算法相比,本文否定选择算法的检测率更高且误检率更低;当目标覆盖率为99%时,3种算法的检测性能较接近,这是因为当目标覆盖率为99%时,所需成熟检测器的数量显著增加,对非自体区域的覆盖增大,处于孔洞区域的数据减少,此时本文否定选择算法的优势不明显。 图3 检测率随期望覆盖率变化曲线 图4 误检率随期望覆盖率变化曲线 由表1可以看出,V-Detector算法在采用不同形状检测器时检测时间均最长,免疫实值否定选择算法的次之,本文、否定选择算法最短;当检测器形状为环形时,本文否定选择算法的检测时间最短。这是因为V-Detector算法由于需要计算各待检测数据与检测器集D中所有检测器之间的距离以判断数据是否异常,因而所需的检测时间最长。 表1 不同算法的检测时间结果对比 免疫实值否定选择算法采用了检测器分级生成方式,在同样的检测率下,需要的检测器数量减少,因而所需的检测时间比V-Detector算法要短。本文否定选择算法由于用聚类中心检测器C代替检测器集D进行距离计算(C的数量远小于D),因而所需的检测时间最短。圆形检测器与环形自体集的形状较相似,匹配度较高,此时孔洞区待检测数据较少,因而检测时间最短。 为提高异常检测的效率,本文提出一种基于检测器集层次聚类的否定选择算法,通过对检测器集进行层次聚类,以聚类中心检测器代替初始检测器集进行距离计算,减少计算时间并对未被检测器覆盖的孔洞区域属性进行进一步判断。实验结果表明,本文否定选择算法较V-detector算法和免疫实值否定选择算法所需时间大幅减少,检测效率提高且误检率降低。下一步将在本文算法的基础上对聚类中心集和检测器集的数量关系进行研究。1.2 改进的否定选择算法
1.3 检测器集的层次聚类
1.4 孔洞数据的判定
2 算法流程
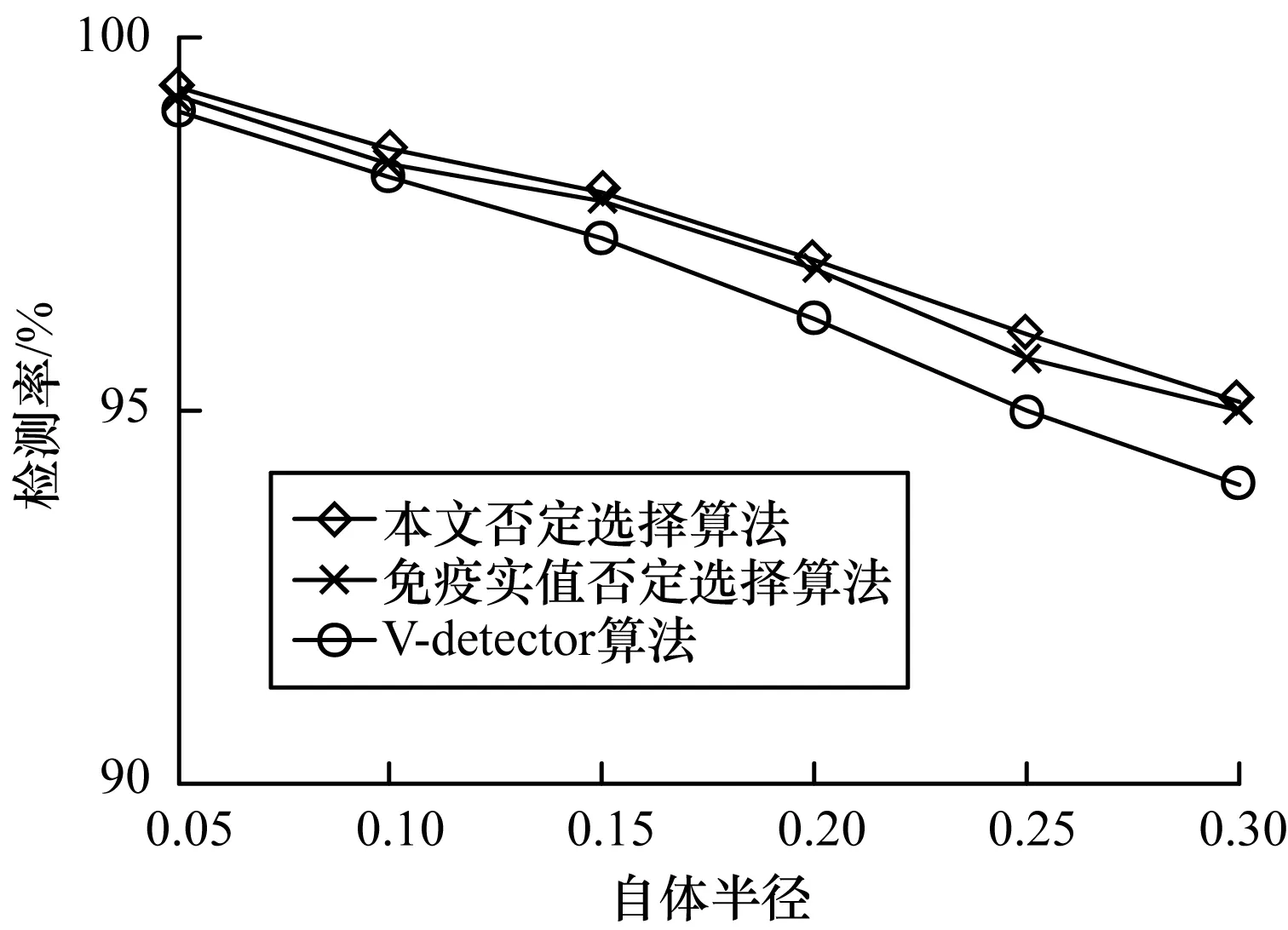
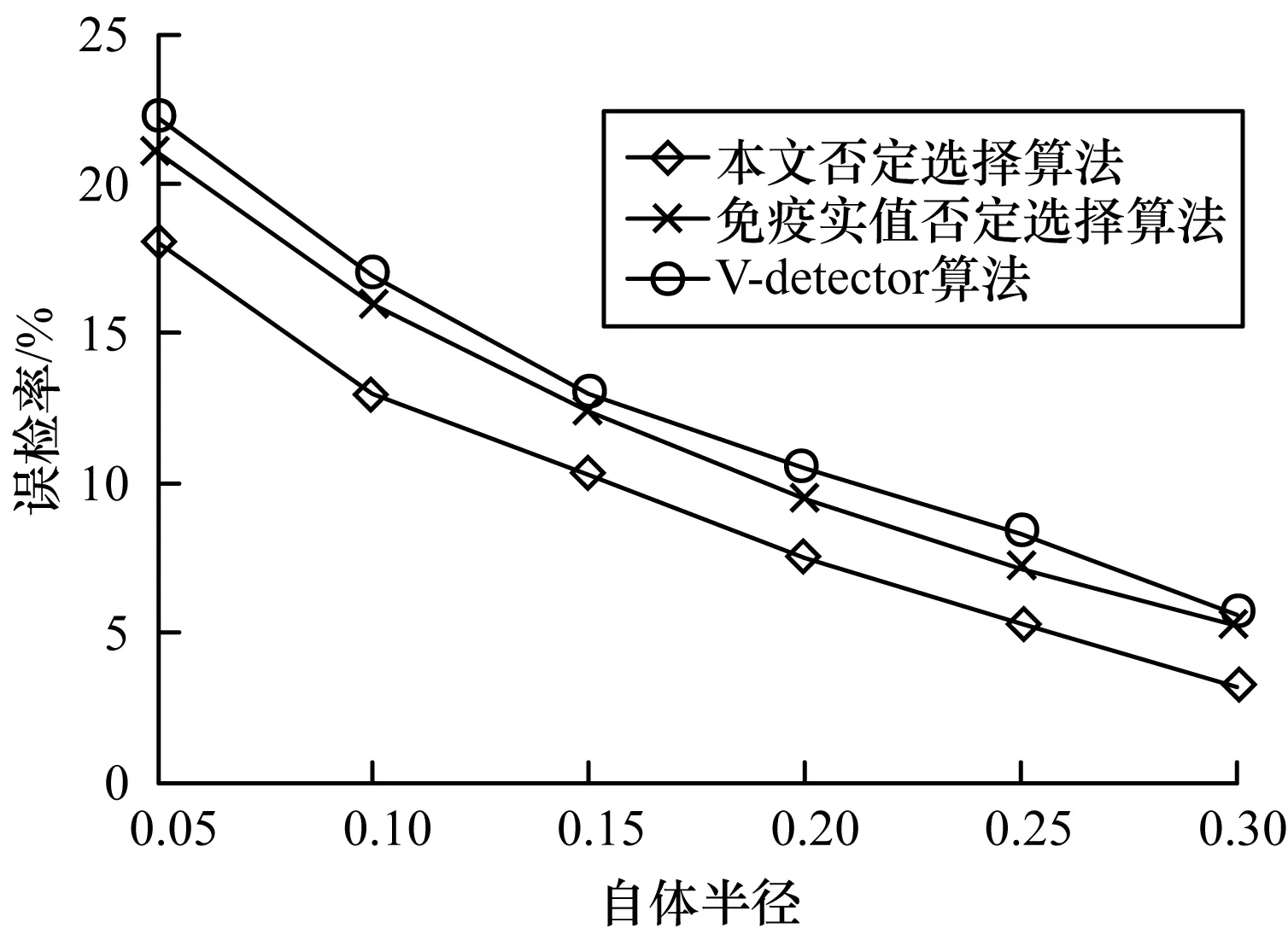
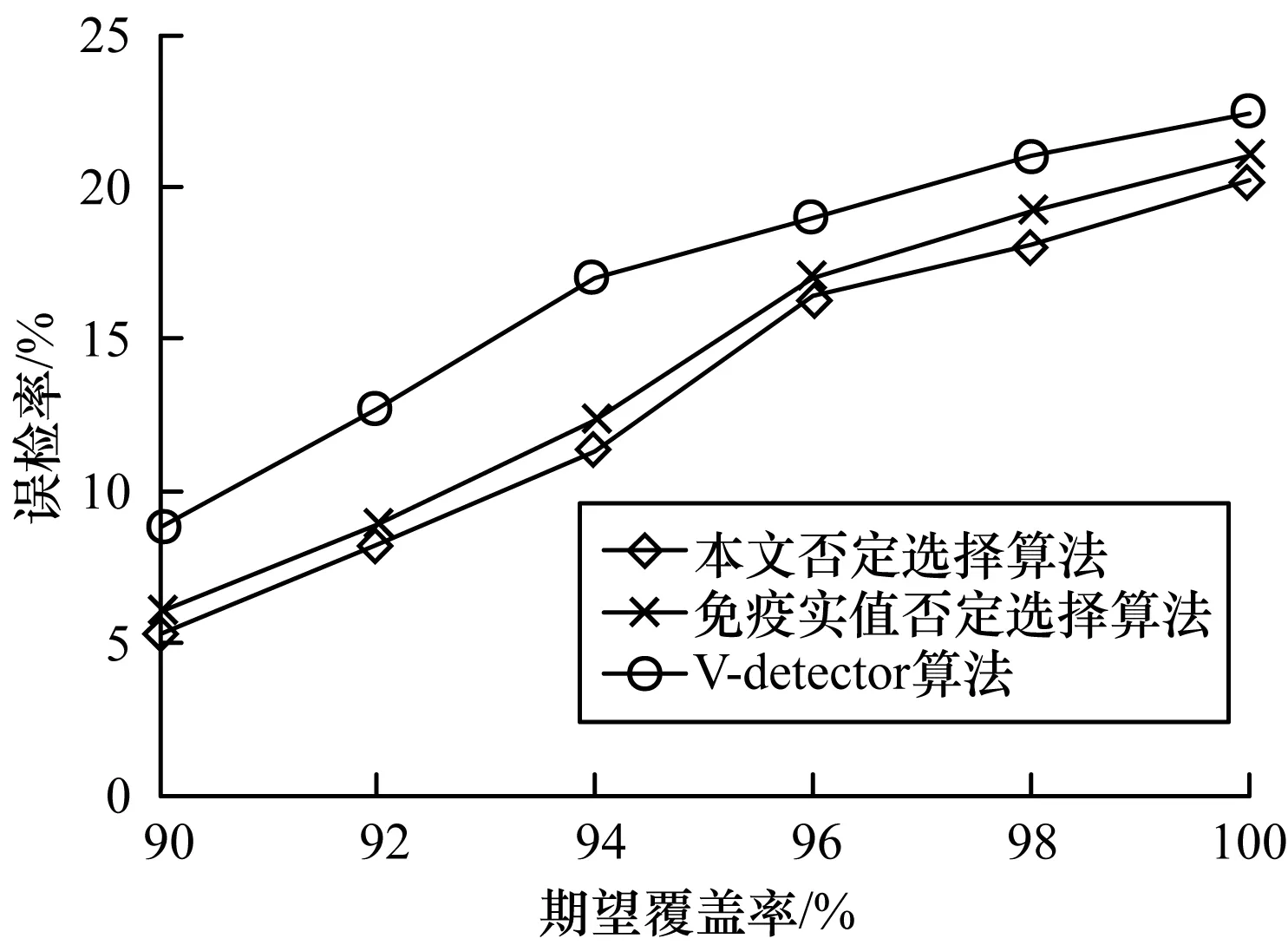
3 实验结果与分析


4 结束语

