基于MIKE 21模型与经验公式在桥梁防洪评价中壅水计算的对比分析

任锦亮 吕 军 张 健

(盐城市水利勘测设计研究院，江苏 盐城 224000)

盐城市南环路通榆河大桥位于江苏省盐城市亭湖区，桥梁跨通榆河而设，位于现有通榆河大桥两侧。由于跨河涉水桥在河道内设墩柱阻水，对通榆河河道行洪排涝有一定影响。根据《中华人民共和国水法》《中华人民共和国防洪法》和国家计委、水利部发布的《河道管理范围内建设项目管理的有关规定》(水政〔1992〕7号文)要求，该工程需进行防洪评价。

在桥梁防洪评价报告编制过程中，壅水分析计算是一项重要内容。目前，桥梁壅水的计算方法很多，主要有经验公式法、数学模型计算法和物理模型试验法。由于数学模型能够较好地模拟复杂地形，因此被广泛应用于桥梁壅水问题的数值模拟计算中。MIKE 21模型是较为成熟的平面二维数学模型。本文以盐城市南环路通榆河大桥工程桥区通榆河河段为例，运用MIKE 21软件进行建桥前后水位变化情况的数值模拟，并将计算结果与《公路桥位勘测设计规范》(JTJ 062—1991)、《铁路桥梁检定规范》中推荐的经验公式的计算结果进行比较分析。

1 研究区域概况

1.1 河流概况

通榆河是里下河地区南北向骨干河道，向里下河地区及渠北滨海、阜宁、响水地区供水，并具有排涝、航运等功能。河道自东台至响水177.7km，属于三级航道，其中东台至废黄河南段河道引水能力为100m3/s，河道底宽50.00m，河道底高程为-4.21m(85高程基准，下同)；废黄河北至响水段河道引水能力为50m3/s，形成三级航道，河道底宽50.00m，河道底高程为-1.21m。

1.2 工程概况

南环路是盐城市城市快速路网工程“一环五射”中“一环”的一部分，南环路全长12.6km。现有南环路跨通榆河大桥上部结构为(50+80+50)m三跨预应力混凝土变截面双箱双室连续箱梁，梁高1.50～4.65m，下部结构采用钢筋混凝土矩形实体式桥墩，钻孔灌注桩基础，桥墩平面尺寸为3.00m(垂直水流方向)×10.50m(顺水流方向)。承台厚度为3.00m，承台顶高程为2.80m，底高程为-0.20m，平面尺寸为10.00m(垂直水流方向)×13.75m(顺水流方向)。桥梁与通榆河垂直相交。

新建南环路跨通榆河主线桥位于现有通榆河大桥两侧，其中跨通榆河主桥上部结构采用悬臂浇筑预应力混凝土连续箱梁，跨径组成为(50+80+50)m，箱梁断面采用单箱单室直腹板形式，桥梁横坡由腹板变高度形成，梁中心高度为2.30～4.60m。主墩采用薄壁空心墩，钻孔灌注桩基础，墩柱断面尺寸为3.50m(垂直水流方向)×6.25m(顺水流方向)。承台厚度为3.50m，平面尺寸为10.00m(垂直水流方向)×11.50m(顺水流方向)，承台顶高程为-1.30m，底高程为-4.80m。

2 模型设计

2.1 模型原理

MIKE 21水动力模型系统是在Boussinesq假定和流体静压假定的二维/三维不可压缩雷诺时均N-S方程的数值解基础上，由连续性方程、动量方程、温度方程、盐度方程和密度方程组成，并通过一个湍流解决方案将方程组闭合。对于水平尺度远大于垂直尺度的情况，由于水深、流速等水力参数沿垂直方向的变化比沿水平方向的变化要小得多，因此，将三维流动的控制方程沿水深积分，并取水深平均值，可得到沿水深平均的二维浅水流动质量和动量守恒控制方程组。下面的控制方程均在笛卡儿坐标系(平面直角坐标系)下给出。连续性方程为

(1)

X方向动量方程和Y方向动量方程分别为

(2)

(3)

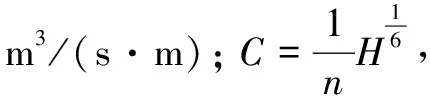
2.2 计算范围

数学模型计算范围应能充分涵盖工程可能要影响的范围及模型边界稳定所需的范围。综合考虑水文资料、地形及工程研究内容等因素，选取南环路跨通榆河大桥上下游各1.2km河段为计算范围。

现状河道断面为2015年7月实测断面，测量间距为100.00m，桥址处加密测量。通榆河设计断面标准为：河道底宽50.00m，河底高程为-4.21m，边坡1∶3(桥址上游600.00m至下游900.00m范围内为1∶4)，青坎高程为2.29m，青坎宽度为15.00m，堤顶高程为3.79m，堤防边坡1∶2.5。

本次模型采用无结构三角形和四边形混合网格剖分,见图1。在建模过程中，将概化处桥墩形状引入模型中，按不过水处理，桥墩周边模型网格自动加密。模型计算网格数为11185个，节点数为5931个。

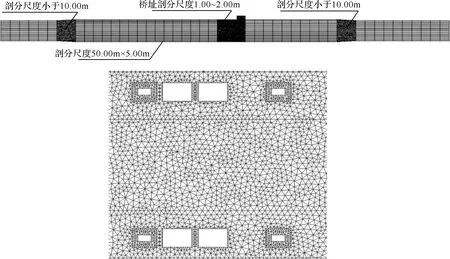
图1 水力计算网格剖分

2.3 模型参数

因为河道狭长，不考虑风力的作用。河道糙率根据率定并参照一定的经验进行取值，桥址上游为自然河坡，青坎以下取0.0225；桥址下游有混凝土护坡，青坎以下糙率取0.0180；青坎以上糙率取0.0300。

2.4 边界条件

模型采用河道设计标准进行计算，上游流量Q=226m3/s，下游20年一遇防洪水位Z=2.425m。支河口潮中河闸站流量为12m3/s。

2.5 桥墩模拟

南环路跨通榆河大桥左右两岸共有8个承台和8个桥墩，老桥4个承台平面尺寸为10.00m(垂直水流方向)×13.75m(顺水流方向)，桥墩平面尺寸为3.00m(垂直水流方向)×10.50m(顺水流方向)；新桥4个承台平面尺寸为10.00m(垂直水流方向)×11.50m(顺水流方向)，桥墩平面尺寸为3.50m(垂直水流方向)×6.25m(顺水流方向)。桥墩模拟三角形边长尺寸为1.00～2.00m，与实际桥墩外形轮廓相吻合。

2.6 检测点布置

为比较建桥前后壅水情况，需在河道中间设置检测点。建桥后桥墩阻水，桥墩处水位变化较大，因此水位检测点放在桥墩处；同时桥墩远离河道中泓，流速较小，因此流速检测点放置在流速较大的河道中央。本次模型共设置了30个检测点，水位点与流速点在水流方向位置一致。检测点示意图见图2。

图2 检测点示意图(单位：m)

2.7 模型准确性分析

由于模型范围较小，无法提供上下游精确的水位流量进行验证，因此采用水力学计算方法对模型的准确性进行评估。

2.7.1 模型计算与曼宁公式对比

为了评估模型计算的准确性，在相同条件下采用水力学曼宁公式进行对比分析。将设计断面放入模型中，糙率取0.0225，用模型算得20年一遇河道流量为170.0m3/s，而用同样的水力要素代入曼宁公式，算得河道流量为169.5m3/s；用模型算得供水工况河道流量为99.0m3/s，而用同样的水力要素代入曼宁公式，算得河道流量为100.0m3/s。模型计算结果与水力学公式计算基本吻合，因此模型流量计算基本正确。

2.7.2 实测断面与设计断面对比

根据实测河道断面，目前桥址上下游通榆河断面河底高程一般为-6.00m，较设计底高程-4.21m相差较大。因此将实测断面与设计断面分别放入模型中进行计算，算得实测断面河道过流能力为227m3/s，规划断面河道过流能力为226m3/s，两者相差并不大。经对比分析，现状桥址上下游断面在防洪水位2.44m时平均过水面积为515m2，而设计断面为513m2，两者基本相同。为方便计算，在本次模型的计算中用设计断面代替现状实测断面。建桥前后河道模型概化图见图3。

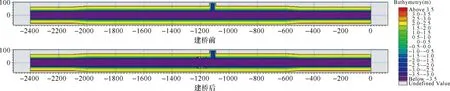
图3 河道模型概化图(单位：m)

2.8 壅水计算

由建桥前后检测点水位变化情况(见表1)可以看出，建桥后桥位上游产生壅水，桥位下游产生跌水。桥前最大壅水高度为0.0062m，壅水长度约1000m。建桥前后水位线、水位差对比情况见图4、图5。

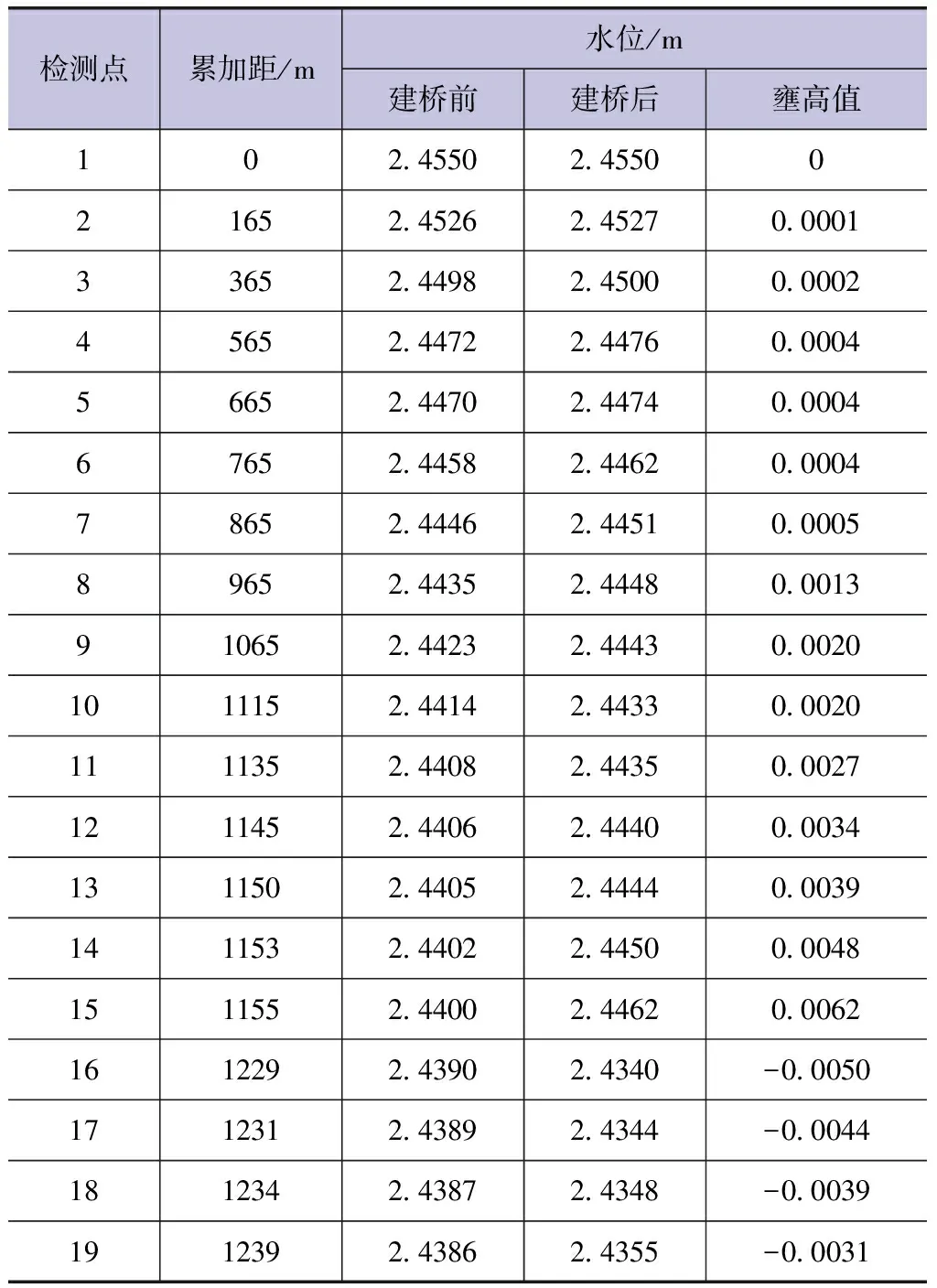
表1 大桥所在河段建桥前后检测点水位变化情况

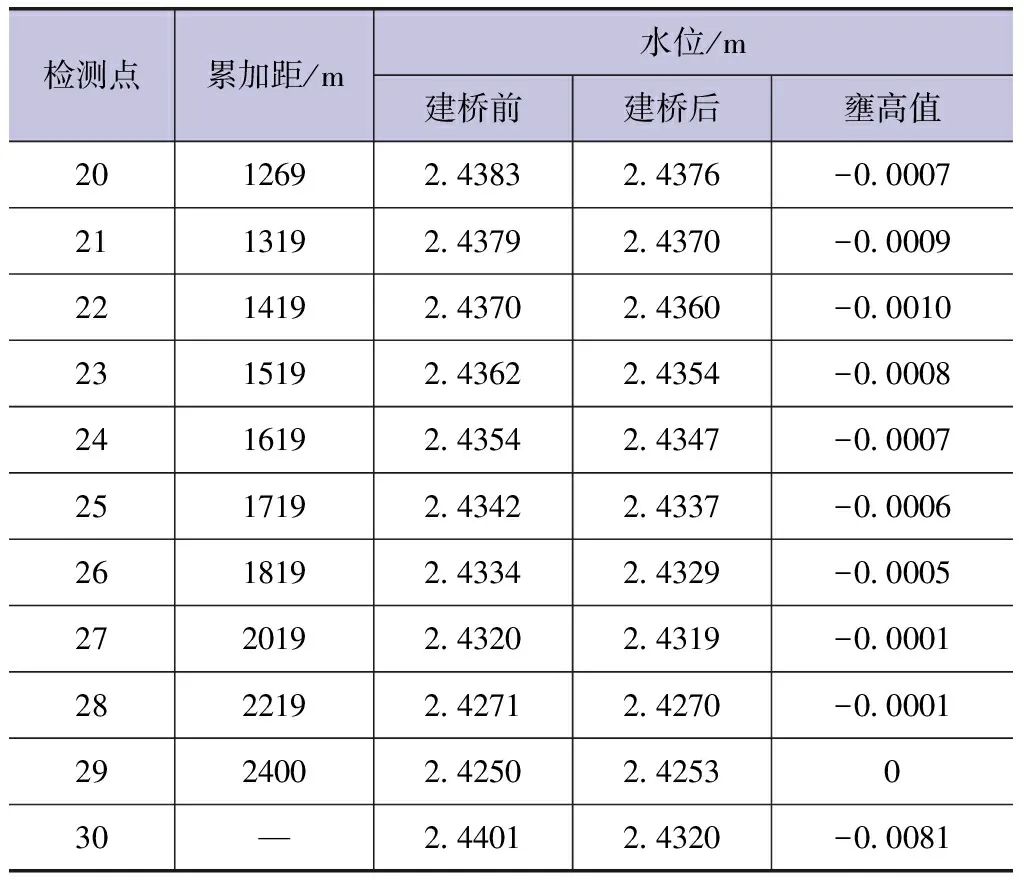
续表

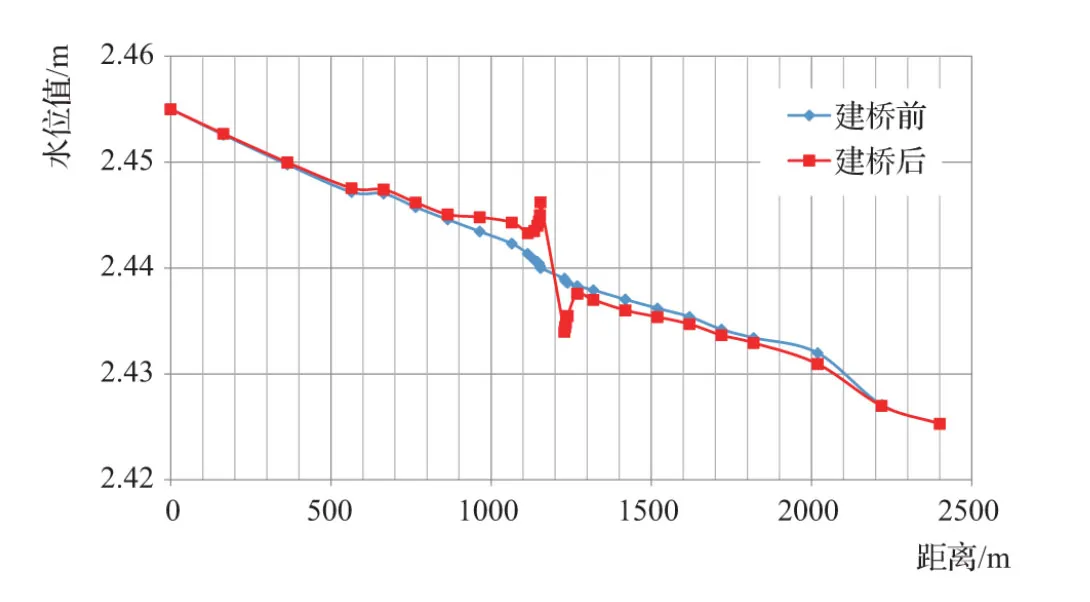
图4 20年一遇建桥前后水位线对比情况

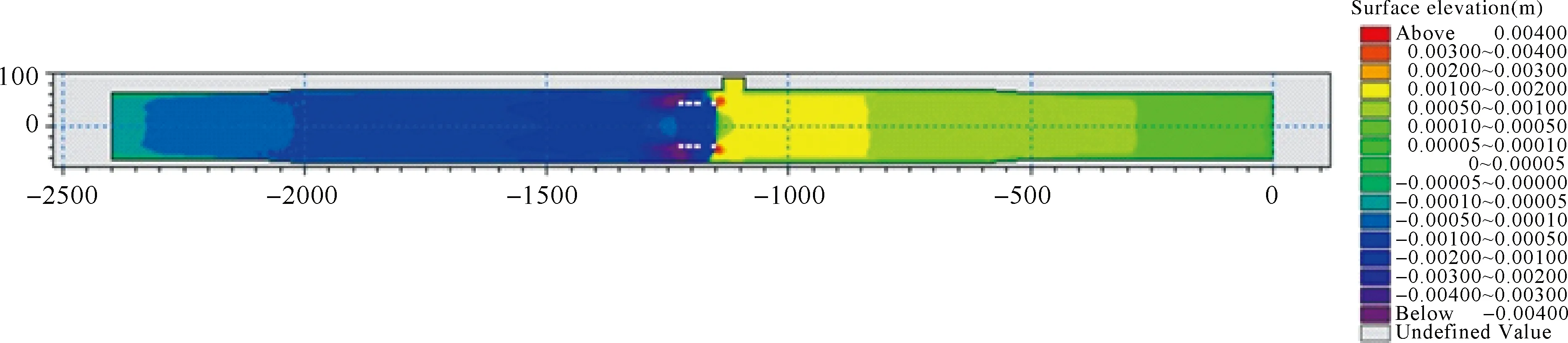
图5 20年一遇建桥前后水位差对比情况(单位：m)

3 规范经验公式计算

工程中常采用经验公式法进行壅水计算，具有参数少、形式简单、便于应用等优点。但桥前壅水高度受河道比降、过水断面尺寸、河床质组成、桥墩形状和布置形式等多种因素的影响，目前还没有被广泛接受的经验计算公式。本文采用《公路桥位勘测设计规范》(JTJ 062—1991)和《铁路桥梁检定规范》推荐的经验公式分别进行桥梁壅水计算。

3.1 经验公式1

根据《铁路桥梁检定规范》，桥前最大壅水高度可按下式计算：

(4)

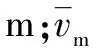
根据《铁路桥梁检定规范》，壅水曲线全长可按下列近似公式估算：

(5)

式中：L为壅水曲线长度,m；ΔZ为桥前最大壅水高度,m；I为水面比降。

3.2 经验公式2

《公路桥位勘测设计规范》(JTJ 062—1991)对桥前最大壅水高度计算推荐了3种不同条件下的经验公式方法。自2015年《公路工程水文勘测设计规范》(JTG C30—2015)发布后，原《公路桥位勘测设计规范》1991版废止，2002版作废，因《公路工程水文勘测设计规范》(JTG C30—2015)中没有壅水分析计算的相关内容，故本处仍采用旧规范中壅水计算方法进行桥前最大壅水高度计算：

(6)

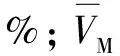
《公路工程水文勘测设计规范》(JTG C30—2015)提供的壅水曲线全长计算公式同《铁路桥梁检定规范》提供的公式(式(5))，这里不重复介绍。

3.3 计算结果

南环路通榆河大桥桥墩为方形墩柱、方形承台，由于老通榆河大桥承台位于地面线以上，按承台进行计算，得到桥墩阻水情况见表2。按经验公式1和公式2分别计算桥前最大壅水高度及壅水曲线长度，结果见表3。经公式1计算，桥前最大壅水高度为0.01234m，壅水曲线长度约2006.9m；经公式2计算，桥前最大壅水高度为0.00630m，壅水曲线长度约1024.4m。

表2 桥墩阻水情况

表3 经验公式法计算结果

4 二维模型与经验公式计算结果对比分析

通过模型计算与两种规范经验公式计算的壅水长度和壅水高度结果对比可以发现，《公路桥位勘测设计规范》公式2壅水计算值与模型计算值基本一致，而《铁路桥梁检定规范》公式1壅水计算结果明显偏大。

两种规范经验公式都具有形式简单、易于计算的优点。《铁路桥梁检定规范》推荐的公式1是在总结现有桥梁公式基础上，通过实测资料验证的最新公式，较《公路桥位勘测设计规范》推荐的公式2优点在于考虑了桥梁压缩程度和河床中冲刷影响的动能折减对桥前壅水的影响。且公式2参数取值的随意性和不确定性较大，会造成壅水计算结果的不稳定。然而在本次桥墩阻水面积比大于20%的情况下，公式2的计算值却更接近二维模型的计算值。故不同经验公式研究背景与考虑因素各不相同，每种经验公式都具有一定的局限性，在本文研究工况条件下，公式2的精度要优于公式1。

5 结 论

本文以拟建的南环路通榆河大桥为例，运用MIKE 21模型对建桥前后水位变化情况进行数值模拟，计算结果符合桥墩的阻水特点。通过对模型壅水计算结果与规范经验公式进行对比分析，本文研究工况条件下，采用《公路桥位勘测设计规范》经验公式壅水计算值与模型计算值基本一致，而《铁路桥梁检定规范》经验公式壅水计算结果明显偏大。

桥梁壅水由于受诸多因素影响，很多因素难以准确求得，经验公式的参数值大多是根据实验资料等方法近似确定，由于研究背景与考虑因素的不同，每种经验公式都具有一定的局限性。MIKE 21水动力数值模型能够较好地模拟复杂地形，因此在区域水文、河道等资料满足要求时，建议采用数学模型计算壅水值。在应用经验公式时应采用多种规范类公式相互验证，以提高桥梁壅水计算的可靠性。