基于压缩感知的探地雷达信号时延估计∗

（新疆铁道勘察设计院有限公司 乌鲁木齐 830011）

1 引言

目前研究人员提出多种探地雷达回波信号时延估计方法，最为常用的是基于快速傅里叶变换和基于匹配滤波的回波信号时延提取算法[6～7]。基于快速傅里叶变换方法的问题在于时延估计的分辨率与系统的工作带宽有关，系统带宽越宽，时延估计分辨率越高，但系统工作带宽同时又受到探测环境和设备尺寸的制约，难以有效平衡。基于匹配滤波方法的问题在于地下各个层次的回波存在时域交叠现象，匹配滤波时延提取过程中，幅值大的回波会遮盖幅值小的回波，严重降低了探测性能[8]。为了解决上述问题，研究人员分别提出多种基于多分辨谱估计的探地雷达时延估计算法，典型方法包括多重信号分类算法[9]和子空间旋转不变法[10]。这些方法的优点在于能够获得很高的时延估计分辨率，且算法抗噪性强，但对探地雷达信号相关性要求很高。

针对探地雷达回波信号时延估计问题，本文提出一种基于压缩感知的探地雷达回波信号时延估计方法。首先，介绍了探地雷达回波信号模型和压缩感知基本理论，论证了应用压缩感知理论解决探地雷达回波信号延时估计的有效性。然后，构建了基于压缩感知的探地雷达信号回波估计模型，并对传统正交匹配追踪算法进行改进，降低基函数错选概率。最后，利用仿真实验验证算法的有效性。

2 探地雷达回波信号模型

探地雷达的基本工作过程为，雷达向待探测地面发射频率很高的电磁信号，信号到达地面后，经过不同层次浅层地板反射，会有时延不同的回波信号返回雷达接收机[11]。因此，接收机接收的回波信号是有不同时延的回波信号组成的，探地雷达回波信号模型可表示为

其中，s(t)为探地雷达发射信号，τk表示第k个回波信号的时延，假设回波信号个数为K，对应K个地表反射面。探地雷达回波信号时延估计的任务就是在接收机接收的回波信号中准确提取出时延参数τk。

实际工作环境中不可避免存在噪声，实际接收机接收的回波信号模型为

其中，n(t)表示探地雷达回波信号中的噪声，可以建模为零均值高斯白噪声。

让，德之主也。让之谓懿德。凡有血气，皆有争心，故利不可强，思义为愈。义，利之本也，薀利生孽。姑使无薀乎！可以滋长。

3 压缩感知基本理论

对于任意一个信号，如果该信号可以表示为少数函数线性组合的形式，则说明该信号具有稀疏性。只有具备稀疏性的信号，才能够进行压缩采样。对于一个稀疏信号，可以表示为

式中，φi为压缩采样后的基函数，θi为基函数对应的系数。压缩感知就是将信号“压缩”到基函数中，压缩后的系数中只有少数的值较大，其他值忽略不影响信号质量。对于一个可压缩信号，可以选用一组基函数进行观测

式中，A表示观测矩阵。信号压缩感知处理过程中，基函数的性能直接影响信号处理质量，为此需要在压缩感知过程中，对基函数进行约束，通常的做法是应用约束等距性理论。经过约束的基函数能够保证信号重构的质量。约束等距性理论为，对于观测矩阵A，如果满足：

则认为其满足约束等距性理论，能够对信号记性压缩采样。其中，δ为介于0和1之间的常数，Θ表示系数向量。信号重构质量是评价信号压缩采样性能的重要指标。信号重构过程可以描述为一个最优化问题：

式中，‖Θ‖0表示l0范数。压缩感知信号重构需要采用优化算法完成，常用的信号重构优化算法为正交匹配追踪算法[12]。

4 压缩感知时延估计

假设雷达发射信号为

压缩感知的基函数字典可以由发射信号的时延构成：

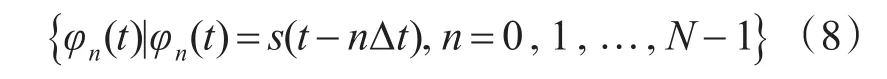
其中，N表示基函数字典中基函数个数，∆t表示时延：

式中B表示探地雷达发射信号的带宽。雷达回波信号压缩采样的过程可以表示为

经过压缩采样后，雷达回波信号可以由基函数字典稀疏表示，假设稀疏度为K，K≪N。

在探地雷达的实际工作过程中，各个浅地层次的回波信号可以由基函数字典中的少量基函数的线性组合表示。信号重构问题可以转化为式（6）给出的最优化问题，文献[13]提出一个最优解转化方法，将l0范数的求解转化为

上式为l1范数的求解。目前，求解压缩感知信号重构的典型方法为贪婪类算法和凸优化类算法，其中正交匹配追踪是应用十分广泛的贪婪类优化算法。针对本文的探地雷达回波信号时延估计问题，本文提出一种基于改进正交匹配追踪的最优化重构算法。

正交匹配追踪算法进行基函数选择的过程中，当多个基函数匹配度相近时，还存在错选基函数的可能。针对探地雷达信号回波压缩感知重构过程中的基函数错选问题，对原始正交匹配追踪算法进行改进。改进后的正交匹配追踪算法步骤介绍如下。

步骤1：初始化。设置初值r0=y，迭代次数P，索引值集合Λ=∅；

步骤2：计算各个基函数的匹配度值，得出匹配度向量，排序后选出前2K个基函数对应的索引值，更新索引值集合Λ；

步骤3：利用最小二乘法实现信号逼近

并按照由大到小排序选择出前K个基函数；

步骤4：计算信号残差

步骤5：判断是否满足迭代停止条件，如满足，寻优结束输出重构基函数；如不满足，返回步骤2，继续迭代，直到满足迭代条件或者达到最高迭代次数为止。

根据压缩感知的约束等距性理论可知，前2K个匹配度高的基函数构成的集合能够近似代表观测信号，因此这种寻优方式选择出的基函数可以保证是最优的。算法的实现流程如图1所示。

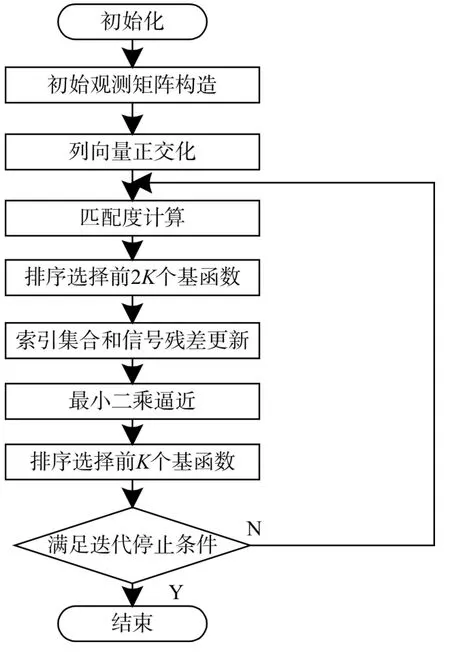
图1 改进正交匹配追踪流程

5 仿真试验分析

为了验证文中提出的基于压缩感知探地雷达回波信号时延估计性能，对其进行仿真实验，并与常用时延估计方法进行性能对比。仿真参数设置如下，探地雷达发射信号调制波形为应用广泛的线性调频脉冲信号，雷达接收机混频输出的中频信号频率f0=25MHz，脉冲信号宽度Tb=0.2us，信号调制带宽B=25MHz。假设雷达回波信号由三个浅层层次的回波分量构成，设定三个回波分量的时延分别为0.459μs，0.821μs和0.842μs，其中第一个回波分量和第二个回波分量的强度为第三个回波分量的2倍，三个回波分量的设定值如图2（a）所示。分别采用匹配滤波方法和文中提出的压缩感知方法估计雷达回波信号时延，信噪比为20dB，估计结果如图2（b）和图2（c）所示。

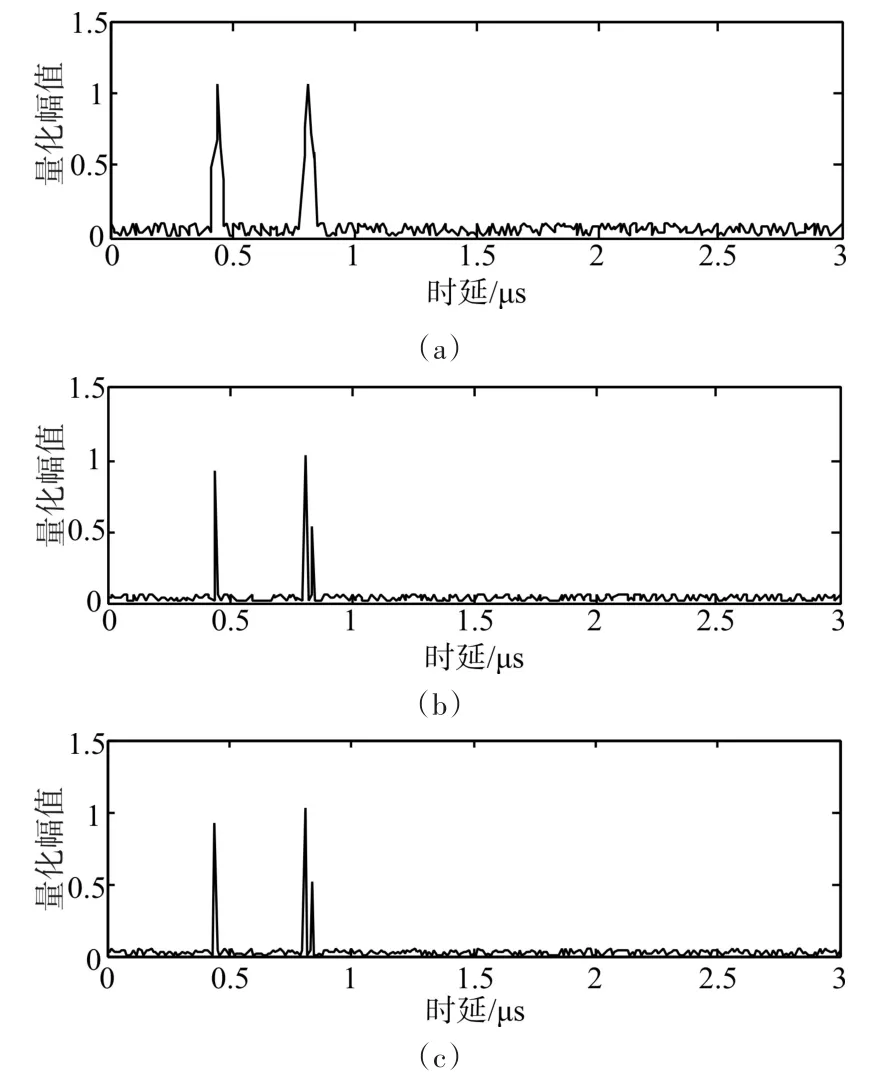
图2 估计结果比较

仿真结果表明，匹配滤波方法能够有效估计出回波分量1和回波分量2，由于匹配滤波旁瓣影响，强回波分量对弱回波分量存在遮盖，匹配滤波方法无法估计出回波分量3。而本文提出的压缩感知回波延时估计方法不受回波分量强度影响，能够有效估计出回波信号中的三个分量。对比图2（a）的回波分量时延位置可知，压缩感知回波时延估计准确，验证了该估计算法的有效性。

首先，测试算法对不同回波分量个数的适应性，回波信号信噪比为20dB，回波分量个数分别设置为1、3、5、8、9、11，每个回波分量个数条件下分别进行100次蒙特卡洛仿真实验，统计各个回波分量的时延估计误差，图3为三种估计方法对各个回波分量时延估计误差的统计结果。

实验结果表明，匹配滤波方法的估计误差随着回波分量个数的增加而增大，这是因为匹配滤波估计方法不能有效应对强回波对弱回波的遮盖，当回波分量个数较多时，回波分量的时延估计性能下降。传统正交匹配追踪和文中提出的改进正交匹配追踪均是基于压缩感知的雷达回波信号时延估计方法，两种方法的估计性能均优于匹配滤波估计方法，且有效克制了强回波分量对弱回波分量的遮盖，估计误差与回波分量个数无关。对比两种匹配追踪算法克制，改进的正交匹配追踪具有更低的估计误差，这是因为改进追踪算法有效避免了传统正交匹配追踪的错选基函数问题，提高了信号重构质量，因此具有更优的时延估计性能。

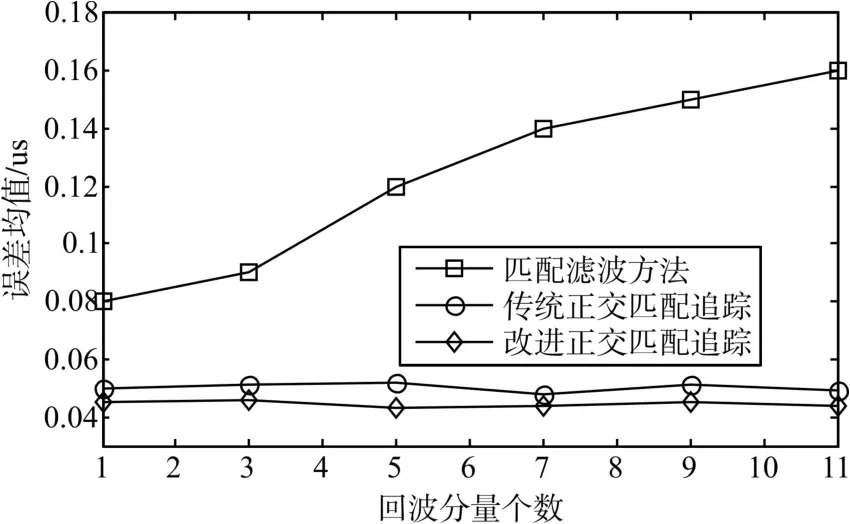
图3 不同回波分量个数条件下估计性能比较

然后，测试算法对噪声的适应性，在回波信号中加入强度不同的噪声，信噪比范围为5dB～25dB，步进5dB，回波分量个数为3，各个信噪比下分别进行100次蒙特卡洛实验，统计3个回波分量的估计误差，图4为回波分量估计误差均值统计结果。实验结果表明，随着信噪比的增加，三种估计方法的误差均呈现出下降的趋势，但匹配滤波算法的估计误差最大，传统正交匹配追踪算法次之，本文提出的改进正交匹配追踪算法的估计性能最佳。实验结果表明文中方法具有优良的探地雷达回波信号时延估计性能。

图4 不同噪声条件下估计性能比较

6 结语

本文研究了探地雷达回波信号时延估计问题，提出了一种基于压缩感知的回波时延估计方法。该方法能够有效避免探地雷达回波时延估计过程中强回波分量对弱回波分量的遮盖，并且通过改进正交匹配追踪提高了基函数的重构质量，提升了回波时延估计精度。仿真实验结果验证了该方法的有效性，为实际探地雷达回波信号时延估计提供了一种新的思路。