一种低能耗与高精确度的WSN数据融合算法
宋 蕾,任秀丽
(辽宁大学 信息学院,沈阳 110036)
0 概述
无线传感网中数据融合[1]是指将同一目标的多个观测数据相互融合,以减少数据冗余并提高系统可靠性[2],进而延长网络生命周期。传感器节点在数据采集、传输与统计过程中,随着网络时延增加、通信量增多和节点生命周期缩短等问题[3],致使数据精确度下降,且节点能耗随之增加。
针对节点能耗和数据精确度问题,文献[4]提出低能耗的E-CPDA算法,在提高数据精确度的同时增加了簇结构动态变化的能耗。文献[5]提出面向车组网的MGDAA算法,通过综合数据的冗余和互补信息来提高融合精确度,但会增加节点能耗。文献[6]提出基于车辆检测器数据压缩重构和交通流特征的Megrez算法,提高了数据精确度,但也增加了节点能耗。针对上述算法存在的问题,本文提出一种基于博弈论的数据融合算法(Data Fusion Algorithm Based on Game Theory,DFABGT)。该算法分为基于博弈论[7]的节点选取和基于贝叶斯理论[8]的数据融合两部分,簇内节点通过收益和能耗确定效益函数选取低能耗节点,再将效益函数的最大值作为权重代入置信距离得到可靠数据。
1 网络模型
在无线传感网中,n个节点构成m个簇结构。簇头收集簇内节点传输的数据,Sink节点融合数据,以保证全局最优[9]。1)传感器节点同构且位置固定,感知半径、通信能力和初始能量相等,每个节点具有唯一ID,且周期性地向簇头传输数据;2)节点非均匀分布,簇头能感知簇内节点的位置与剩余能量,簇内节点能感知自身剩余能量;3)不论剩余能量是否有限,能耗控制均需在节点承受的能量范围内;4)节点自感知且主动收集数据,Sink节点没有能量限制。网络模型[10]如图1所示。

图1 网络模型
2 DFABGT算法
DFABGT算法分为基于博弈论的节点选取和基于贝叶斯理论的数据融合两部分。基于博弈论的节点选取以降低能耗为目标,簇内节点通过效益函数最大值选取最佳策略。基于贝叶斯理论的数据融合以提高数据精确度为目标,簇头通过置信距离选取有效数据传输给Sink节点,并采用贝叶斯融合数据。
2.1 基于博弈论的节点选取
簇内节点通过收益和能耗相互博弈选取最佳策略得到低能耗节点。博弈论[11]的基本要素为参与者、策略和效益函数。参与者指需要决策的个体,即簇内节点。策略指具体规则,令节点具有选择善意融合(Good Fusion,GF)、恶意融合(Bad Fusion,BF)与不融合(Not Fusion,NF)的能力,记为S={GF,BF,NF}。效益函数指行动函数,以判断不同策略的期望值。效益函数由收益和能耗构成,具有如下要素:
要素1收益(α)用于判断节点是否参与数据融合处理,其中,αi=1表示第i个节点参与融合处理,αi=0为不参与融合处理,收益集合记为{α1,α2,…,αn}。
要素2善意融合能耗WG表示节点融合数据包的能耗。
要素3恶意融合能耗WB表示由于链路信道、节点或数据包遭受网络攻击导致融合呈现恶意结果,其能耗值为融合数据包的能耗与网络攻击的能耗(WA)。
要素4不融合能耗WN表示任意两个节点中若有一个节点不参与融合,则另一个节点有融合能耗但没有收益;若两个节点均不参与融合,则节点均没有收益或能耗。
不同策略组合形成的效益值构成博弈策略(如表1所示),说明如下:
1)假设节点i与节点j均选择融合策略时,节点i与节点j均有收益(αi=αj=1)且为对方付出相应的融合能耗;当节点i选择融合策略、节点j选择不融合策略时,节点i与节点j均没有收益(αi=αj=0),节点j付出不融合能耗但节点i付出相应的融合能耗。
2)假设节点i选择不融合策略、节点j选择融合策略时,节点i与节点j均没有收益(αi=αj=0),节点j付出不融合能耗但节点i付出相应的融合能耗;当节点i与节点j选择不融合策略时,节点i与节点j均没有收益(αi=αj=0)或能耗。
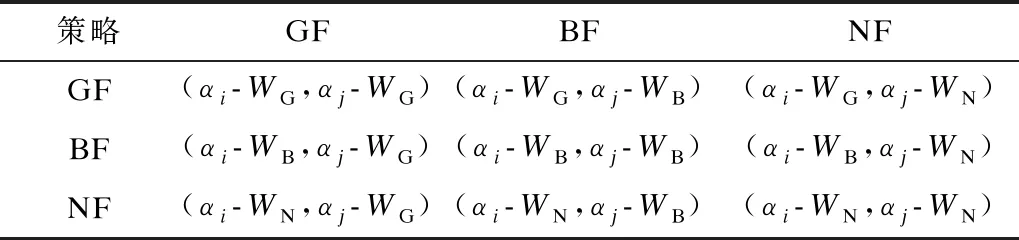
表1 博弈策略
参与融合的任意两个节点中一个节点选择善意融合、恶意融合与不融合的概率为β1、β2、β3,且β1+β2+β3=1表示全部的决策内容;另一个节点选择善意融合、恶意融合与不融合的效益函数记为p(GF)、p(BF)、p(NF),计算公式如下:
p(GF)=β1×(1-WG)+β2×(1-WG)+β3×WG
(1)
p(BF)=β1×(1-WB)+β2×(1-WB)+β3×WB
(2)
p(NF)=(β1+β2+β3)×WN=WN
(3)
因为WB=WG+WA,所以WB>WG恒成立,通常令WN=0,不论βi(i=1,2,3)取何值,总存在p(GF)>p(BF)>p(NF)。簇内节点通过多轮博弈剔除不融合节点,降低节点能耗。
2.2 基于贝叶斯理论的数据融合
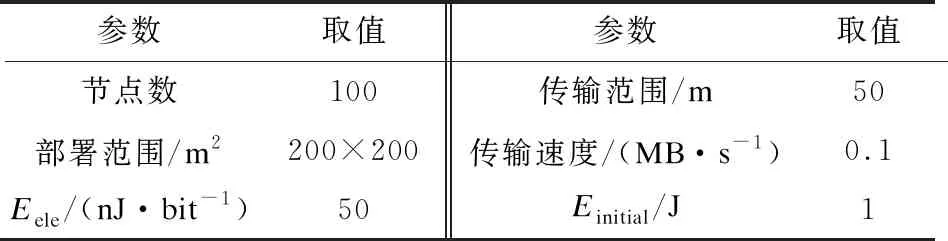
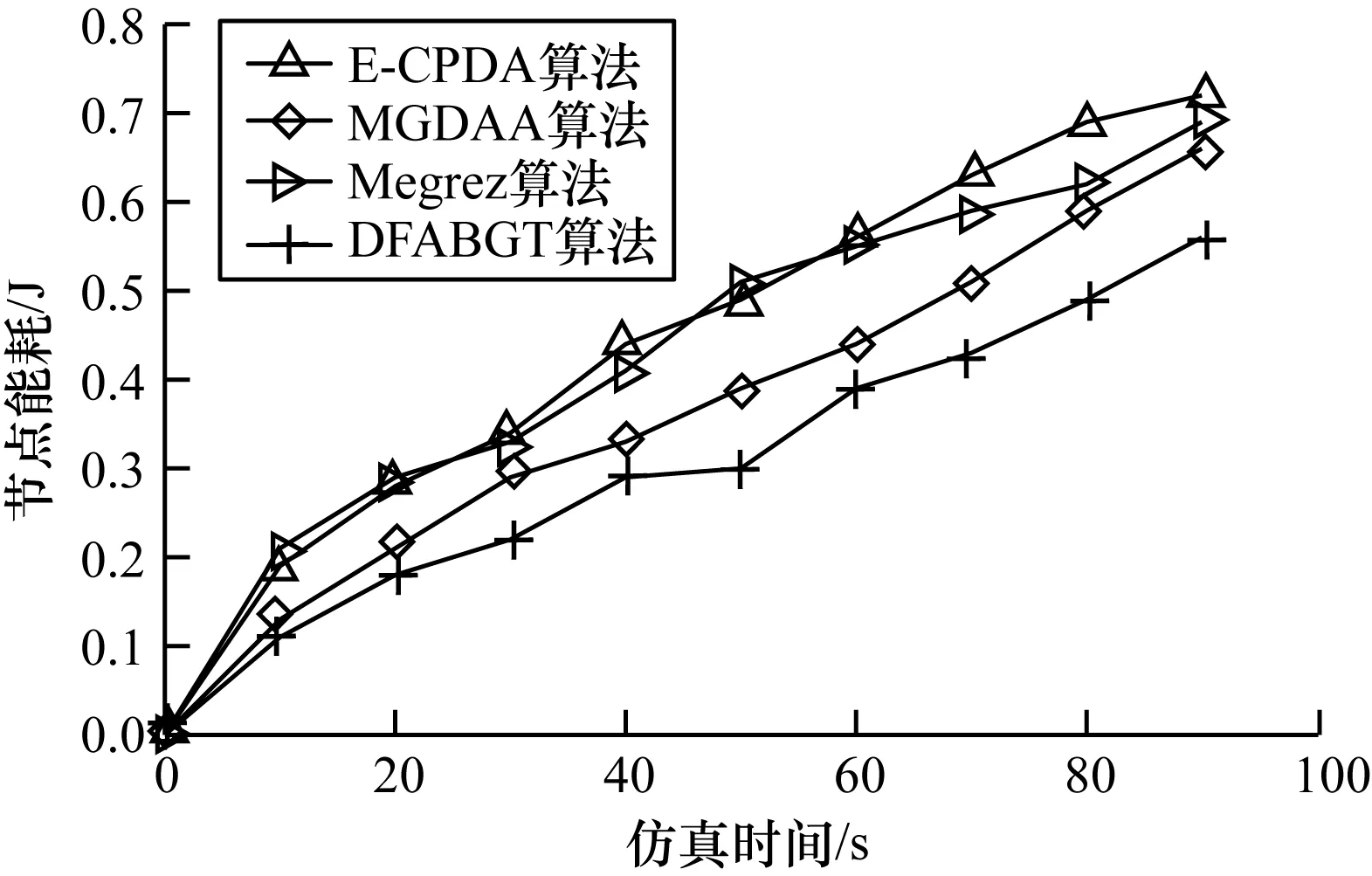
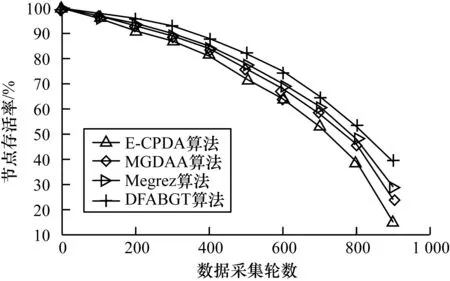
通过博弈论选取低能耗节点的方式不能保证采集数据均可靠,因此簇头需通过置信距离筛选可靠数据,提高精确度。置信距离[12]基于预判测量数据与实际数值的紧密程度,确保采集数据接近实际结果。令xi、xj为一次测量中第i个和第j个节点的输出,且i (4) 其中,分母用作归一化处理,分子中的概率密度函数定义如下: (5) 效益函数最大值p(GF)作为权重代入概率密度函数,确保节点在善意融合的前提下得到有效数据。当xi=xj时,dij=0;当xi≠xj时,dij∈(0,1)。定义二值变量rij为第i个节点输出数据对第j个节点输出数据的支持程度,通过融合结果确定阈值α与rij,具体公式如下: (6) 其中,1表示第i个节点的输出数据支持第j个节点的输出数据;0表示第i个节点的输出数据不支持第j个节点的输出数据。 假设节点的临界数为m,对n个节点中任意两个节点采集的数据计算置信距离得到m×m的二值关系矩阵,表示节点输出数据间的相互支持程度,筛选出l个有效数据。 (7) (8) DFABGT算法流程如图2所示,具体步骤如下: 步骤1在一轮博弈中,节点从善意融合、恶意融合与不融合中选择一个策略,依据能耗与收益计算效益函数。 步骤2通过效益函数值剔除不融合节点降低能耗。 步骤3将效益函数最大值作为权重代入置信距离公式,确保参与融合的节点均是善意融合且相互支持度最高。 步骤4依据融合结果确定阈值,将置信距离向量和阈值进行比较得到二值关系向量,构成二值关系矩阵。 步骤5由二值关系变量剔除小于阈值的置信距离值并且筛选有效数据,簇头节点将有效数据传输给Sink节点。 步骤6Sink节点采用贝叶斯理论融合数据得到融合结果。 步骤7为避免筛选善意或恶意融合节点,需要重复上述步骤完成多轮博弈,直至剩余节点均不融合时为止。 图2 DFABGT算法流程 将100个节点随机分布在200 m×200 m中,Sink节点部署在(100 m,100 m)处,处于集群中心且剩余能量最大的节点设置为簇头[14]。在OPNET仿真环境[15]下对DFABGT算法与E-CPDA算法、MGDAA算法及Megrez算法进行对比,仿真参数如表2所示。 表2 仿真参数设置 依据文献[16]中数据精确度定义,数据精确度等于融合前后的数据累和之比。考虑到贝叶斯理论,本文采用均值与方差作为判断融合结果精确度k的依据,具体计算如下: (9) 图3 数据融合算法的融合结果精确度比较 由图3可知,DFABGT算法、E-CPDA算法、MGDAA算法与Megrez算法的融合精确度随着节点数的增多均呈上升趋势。在传感器节点数为10~90时,DFABGT算法相比E-CPDA算法、MGDAA算法与Megrez算法精确度上升均值为3.9%、21.2%和12.1%。E-CPDA算法通过降低节点在通信过程中的碰撞几率提高精确度,但其未筛选数据;MGDAA算法通过改变簇结构冗余度和结构变化度从而破坏原始数据;Megrez算法中的压缩和重构过程破坏了原始数据;DFABGT算法在筛选原始数据时并没有破坏和构造数据,因此其精确度高于其他算法。 本文在无线传感网中采用简单的能耗模型[17],忽略节点在计算、存储等过程中的能耗,仅计算节点随着通信时间增加所消耗的能量。假设节点传输lbit数据经过的距离为d(20≤d≤25),数据融合过程中的节点能耗公式如下: (10) ERx_elec(l)=lEelec (11) 其中,ETx(l,d)为发送端经过距离d发送lbit数据的能耗,ERx_elec(l)为接收端接收lbit数据的能耗,d0=25 m为阈值,Eelec为节点收发每比特数据的能耗,εfsd2与εmpd4为信号自由空间模型和多径衰减模型中信号放大器的能耗参数[18]。当发送端与接收端的距离小于阈值时,采用自由空间的通信方式,发送端能耗与距离的平方成正比;否则采用多径衰减的通信方式,发送端能耗与距离的4次方成正比。 假设融合单位比特数据的能耗为EDA,由此可知EDA的取值范围为(0,ETx(l,d)+ERx_elec(l))[19],那么善意融合的能耗取值范围为(0,lEDA),恶意融合的能耗总是大于善意融合的能耗,而不融合的能耗为0。节点能耗的变化曲线,如图4所示。 图4 数据融合算法的节点能耗比较 由图4可知,DFABGT算法与E-CPDA算法、MGDAA算法和Megrez算法比较,节点能耗分别降低28%、22%和19%。E-CPDA算法通过减少通信传输量降低能耗,导致存在额外簇结构的能耗;MGDAA算法与Megrez算法以节点能耗为代价换取数据精确度,但却未兼顾节点能耗问题,而DFABGT算法通过融合能耗进行博弈来降低节点能耗,且未产生额外能耗。综上,DFABGT算法的能耗低于其他算法。 网络生命周期用于衡量负载均衡情况,本文采用文献[20]的定义,认为网络生命周期为首个节点的失效时间。网络中节点存活率的变化情况如图5所示。 图5 数据融合算法的网络生命周期比较 由图5可知,DFABGT算法与E-CPDA算法、MGDAA算法和Megrez算法进行比较,网络生命周期分别延长5%、3.1%和4.8%。E-CPDA算法、MGDAA算法和Megrez算法未筛选节点与数据,因此增加了能耗,且E-CPDA算法增加了簇结构的能耗,而DFBAGT算法通过选取节点、筛选数据,大幅度降低节点能量的消耗,使得节点存活率下降幅度低于其他算法。综上,DFABGT算法的网络生命周期更长。 本文从提高数据精确度和降低节点能耗两方面着手,提出基于博弈论的数据融合算法,簇内节点以收益和能耗为效益函数的输入参数进行博弈。通过效益函数最大值选取低能耗节点,对这些节点进行置信距离的计算来筛选有效数据参与融合处理。簇头将有效数据传输到Sink节点,由Sink节点采用贝叶斯理论融合数据。实验结果表明,本文算法能有效提高数据精确度,降低节点能耗,延长网络生命周期。下一步将考虑数据的安全隐私特性,在实现数据精确融合的同时保障数据安全。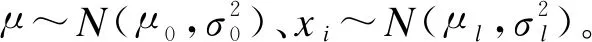
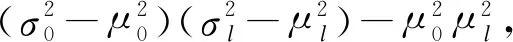
2.3 DFABGT算法实现

3 算法仿真与性能分析
3.1 数据精确度
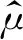

3.2 节点能耗
3.3 网络生命周期
4 结束语

