基于预约策略的港外集卡送取箱双目标优化模型

张 赫，邢江豪，闫建鑫，王 宇

(大连海事大学交通运输工程学院，辽宁 大连 116026)

随着港口吞吐量的逐年增长，集卡调度在港口的集疏港作业中显得越来越重要.在作业高峰时段，大量非平稳到达的集卡从各公路系统汇集到港口，造成公路系统以及闸口和码头堆场的排队拥堵[1-2].这不仅制约了港口货物集疏运速率，而且导致了集卡在码头的滞留，加重了二氧化碳等汽车尾气对大气造成的破坏.鉴于此，中外学者对预约机制下的港外集卡调度进行了一系列探讨和分析，得出了许多研究成果.曾庆成等[3]对集卡到达的规律使用非平稳排队模型，以遗传算法(genetic algorithm，GA)与驻点固定流体近似算法确定最优的预约份额.范厚明等[4]针对基于预约机制的送箱集卡多集装箱码头调度问题，以集卡数量最少化为目标函数建立集卡调度模型，并用改进的蚁群算法(ant colony optimization，ACO)求解.张赫等[5]将港口系统和公路运输系统进行整体调度优化，以最小化集卡工作时间为目标，将集卡调度运作路径进行了优化处理，增加了港公系统的运作速率.Namboothiria等[6]通过将车队运输费用最优化，来建立集卡调度模型，并指出了集卡车队在考虑预约机制因素下调度的影响.Kim等[7]通过分析得出利用M/G/1排队模型来建立集卡在堆场的排队过程.Chen等[8]考虑了集卡抵达受时间影响的特点，构造了预约机制下集卡非平稳排队模型，提出了集卡抵达分布、高峰时段阻塞缴纳费用的集卡控制办法.

综上研究为预约机制下的港外集卡调度优化提供了依据，但目前的研究都是针对集卡到达港口完成送箱或取箱的问题，而现实状况下往往是集卡往返于单一港外堆场与多个码头堆场之间的同时进行送取箱操作.本文在上述研究基础上，提出了港外集卡在预约时间窗下到达港口堆场内多个进出口箱区的优化调度问题，使得该问题的探讨更符合现实情况.

1 预约时间窗下集卡送取箱优化模型

1.1 问题描述

现将堆场内的箱区根据其目的地统一分为两种，一种是存放从船上卸下集装箱的进口箱区，另一种是存放等待装船集装箱的出口箱区.港口通过获取船舶到港时间以及集装箱的装卸量，并以此为依据为各进、出口箱区设定港外集卡的预约时段和各时段的预约份额[9].所有港外集卡都从港外堆场出发，首先，必须在预约时间窗下将港外堆场的集装箱运送至出口箱区，然后再判断是否满足进口箱区的预约时间窗与预约份额的限制，若满足，则到达进口箱区完成取箱操作，返回港外堆场，完成一次送、取箱任务.若不能满足预约时间窗的限制，则由港外堆场单独安排集卡完成任务.问题描述如图1所示.

本文考虑在预约机制下，单一港外堆场与多个具有不同送取箱需求的进、出口箱区的港外集卡调度问题.在预约时间窗与预约份额确定的条件下，合理安排港外集卡，求得港外集卡数量与所有港外集卡送取箱总时间相对应的成本最小值，以减少集、疏港过程中的资源消耗.

图1 港外集卡送取箱示意图Fig.1 Schematic diagram of the deliver and pickup container of the trucks

1.2 问题假设

1) 由于在不同时间段内，船舶到达码头的数量不均衡以及受到其他非平稳因素的影响，预约时间窗与预约份额在不同时段内存在较大的波动，故只考虑一个时段内的时间窗划分.

2) 各进出口箱区在该时段内的预约时间窗连续且各时间窗长度相同，预约份额确定.

3) 整个过程中，港外集卡的时间消耗主要是从港外堆场到港口的往返行程时间、闸口排队时间、码头停车场等待时间、装卸箱时间、进与出口箱区间行程时间.集装箱的装卸时间由场桥的运作时间决定并设为确定值.港外堆场到港口的往返时间与进、出口箱区间的行程时间统一成为集装箱运输时间，并由行程距离与港外集卡平均速度的比值确定.闸口排队时间和码头停车场等待时间统一成港口排队等待时间，并取各集卡等待时间的平均值[10-12].

4) 该时段的时间长度小于集卡从港外堆场到港口的行程时间最小值的三倍.

5) 所有港外集卡的出发时刻相同，且不考虑集卡的不确定因素，即假设所有集卡都能准时到达[13].

6) 各进、出口箱区的取、送集装箱数量必须在该时间段内完成，该时段内各进、出口箱区的时间窗划分确定且不可改变[14].

1.3 参数定义

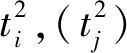
1.4 模型建立

1.4.1 目标函数的确定 目标函数的公式为：

(1)

1.4.2 约束条件 为满足各码头堆场的送、取箱需求以及预约时间窗限制，约束条件表示如下：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

∀i∈N，∀j∈M，∀l∈L；

(12)

(13)

(14)

(15)

(16)

在上述模型中，式(1)为目标函数，求得所有港外集卡完成集、疏港任务所消耗的总时间与调用集卡数量的成本最小值.式(2)、(3)与(4)表示一辆集卡单次最多到达两个不同任务的箱区完成送、取箱任务.式(5)表示到达出口箱区i的集卡数量必须满足该箱区的送箱总量.式(6)表示到达进口箱区j的集卡数量必须满足该箱区的取箱总量.式(7)表示集卡单次到达两个箱区完成送、取箱任务的数量，小于所有到达出口箱区的集卡数量与所有到达进口箱区的集卡数量两者的较小值.式(8)表示所有集卡都从港外堆场出发.式(9)表示所有集卡完成任务后都返回到港外堆场.式(10)表示集卡到达进口箱区完成送箱任务必须在到达出口箱区之前.式(11)表示集卡从港外堆场出发到达出口箱区i的时刻.式(12)表示集卡从出口箱区i出发到达进口箱区j的时刻.式(13)表示集卡从港外堆场出发到达进口箱区j的时刻.式(14)确保集卡从港外堆场出发到达出口箱区i的时刻满足该箱区的预约时间窗要求.式(15)确保集卡从出口箱区i出发到达进口箱区j的时刻满足该箱区j的预约时间窗要求.式(16)确保集卡从港外堆场出发到达进口箱区j的时刻满足该箱区的预约时间窗要求.

2 算法设计

遗传算法是一种应用广泛的启发式算法，对于大规模优化问题的求解具有高效稳定的特点.本文采用改进的遗传算法对模型进行求解，将港外集卡的调用数量与所有港外集卡所消耗的时间总和来构造适应度函数，并通过直接保留精英染色体的方式加快算法的收敛速度.算法的具体步骤如下.

步骤1编码与初始种群.

染色体的基因为各进出口箱区的编号，每条染色体采用自然数编码，并用自然数的大小表示进出口箱区，其中0代表港外堆场.例如(0 1 6 0 2 7 0 3 8 0 4 0 9 5 0 10 0)表示：自然数1至5为出口箱区，自然数6至10为进口箱区，两者相互交替排列.共调用6辆集卡，调度方案为0-1-6-0，0-2-7-0，0-3-8-0，0-4-0，0-9-5-0，0-10-0.为简化编码过程，可先不考虑港外堆场的编码，将染色体直接表示成(1 6 2 7 3 8 4 9 5 10).最后使用两次随机数，在满足交替排列的前提下，生成各进、出口箱区独立的自然数随机排列，完成初始化种群.

步骤2港外集卡数量car_num与消耗总时间all_time的计算.

先为N个出口箱区安排一辆港外集卡，再按染色体中基因排列的顺序调配港外集卡，若港外集卡只能满足出口箱区的时间窗则该港外集卡完成送箱任务后直接返回港外堆场，另外调配一辆空集卡来完成进口箱区的取箱任务.若港外集卡完成送箱任务后，还能满足下一个进口箱区对应基因的时间窗，则该集卡继续完成取箱任务，再返回港外堆场.每当有集卡返回港外堆场就更新港外集卡数量和港外集卡消耗总时间：car_num=car_num+1，all_time=all_time+该集卡此次消耗时间.

步骤3适应度函数计算.

通过对步骤2港外集卡数量car_num与消耗总时间all_time的加权求得整体总成本，并将其倒数作为个体的适应度值.

步骤4选择操作.

采用精英策略，直接保留父代中的最优个体，并用轮盘赌算法从父代中选择个体进入子代交配池.

步骤5交叉操作.

由于两个染色体的基因片段随机交叉后容易出现基因重复的现象，故要对交叉后的染色体进行消去冲突操作.并且染色体中的基因是由两种类型交替排列的方式组成，因此，消去冲突时需要考虑基因的排列方式.具体交叉过程如图2～图4所示.

1) 随机设定两个交叉点——点1和点2(如图2).

图2 随机设定交叉点
Fig.2 Randomly set the intersection

2) 染色体基因片段交叉(如图3).

图3 基因片段交叉Fig.3 Gene fragment cross

3) 消去冲突点——点3和点4(如图4).

图4 消去冲突Fig.4 Eliminate conflicts

步骤6变异操作.

按照非均匀的变异概率将染色体中的进口码头基因与出口码头基因分别随机交换.非均匀变异概率P由进化代数自动调整.

其中pmax，pmin为设定的初始变异概率，Tnow为当前进化代数，Tmax最大进化代数.

步骤7终止条件.

迭代到设定次数时终止算法.

3 算例分析

3.1 算例描述

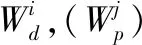
表1 各堆场间的行程时间表Tab.1 Itinerary schedule between terminal yards min

表2 各码头堆场集港信息Tab.2 Terminal yards information

3.2 结果分析

该算例实验在Anaconda下用Python编程求解，并在Intel 酷睿i5-4200u处理器，主频1.6 GHz，内存4 GB的计算机上运行.经过200次迭代与经过300次迭代，得到的收敛结果分别如图5和图6所示.

图5 GA算法进化200代的结果Fig.5 GA algorithm evolution 200 generation results

图6 GA算法进化300代的结果Fig.6 GA algorithm evolution 300 generation results

从图中结果分析得出，随着迭代次数的增加，种群中的染色体逐渐收敛稳定于最优值.当进化到300代时，输出的算例最优值达到最小并且处于收敛状态，此时得出的港外集卡调配方案见表3.港外集卡消耗总时间最优值为638 min，调配的集卡数量为10辆，最小成本为11 380.得到了在预约窗口下的港外集卡最优调度方案，达到了节省系统作业成本的目的，从而证明该算法是有效的.

表3 港外集卡最优调配方案表Tab.3 The optimal scheduling of trucks

运用同样的算例，在相同的设备下，采用蚁群算法求解，并与本文遗传算法求解结果进行比较，其结果见表4.

从表中可以看出，在相同算例下，两种算法都得到了相同的最优结果，但在不同迭代次数间，用遗传算法求解的结果相对于蚁群算法更贴近于最优结果，并且迭代的速度更快.

3.3 算例规模随机性分析

为避免算例规模的单一性造成随机性结果，将上述算法应用于不同规模的算例进行分析，如将上述问题扩展为算例1和算例2.算例1：30个箱区，其中 10个进口箱区，份额为20个集装箱；20个出口箱区，份额为32个集装箱.算例2：50个箱区，其中20个进口箱区，份额为40个集装箱；30个出口箱区，份额为40个集装箱.

表4 ACO与GA结果比较Tab.4 Comparison of ACO and GA results

新增的两个算例，在算法进化200代后，收敛结果如图7和图8所示.对于30个箱区算例，港外集卡消耗总时间最优值为2 176 min，调配的集卡数量为35辆，最小成本为39 260.对于50个箱区算例，港外集卡消耗总时间最优值为3 200 min，调配的集卡数量为54辆，最小成本为59 000.两种算例都得到了在预约窗口下的港外集卡最优调度方案，从而证明该算法通过了随机性验证，算法是有效的.

图7 30个箱区GA算法进化结果Fig.7 30 container block GA algorithm evolution results

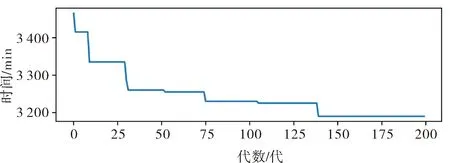
图8 50个箱区GA算法进化结果Fig.8 50 container block GA algorithm evolution results

4 结论

在港口与船舶以及港外堆场都建有预约机制的情况下，港方能够获取船舶靠港时间、装卸箱数量等集、疏港信息，并以此为依据，综合考虑港外堆场的实际运输能力，制定合理的集卡送取箱预约计划.将有效降低集卡非平稳到达情况下造成的港口排队拥堵，减少系统碳排放量，提高集疏港作业效率.本文针对预约时间窗下港外集卡多进、出口箱区的调度问题，建立了数学模型，并用改进的遗传算法求解.算例结果证实模型是有效的，设计的遗传算法也能较快地收敛到全局最优解.通过合理调配集卡在某时段内到达的进出口箱区，能够减少集卡数量与所有集卡的消耗时间，提高集卡的运输效率，降低港口设施空耗.这些优化结果可以为将来的港外集卡送、取箱调度提供理论参考依据.本文没有将港外集卡在闸口和堆场处的实际排队规律、时间窗滚动分布、场桥作业规律等问题构建到模型中，因此需要对这些问题做进一步的综合研究.