四阶电力系统混沌分析与新型滑模控制

方 洁，许丹莹，方 娜，邓 玮

(郑州轻工业大学电气信息工程学院，郑州 450002)

混沌是非线性系统特有的运动形式，具有内在随机性、分形性质、敏感依赖性等特点，在不同的初始值和系统参数下会产生多种不同的混沌运动状态，如多种周期运动共存[1]、混沌与周期运动共存[2]、多吸引子共存[3-4]等.电力系统作为一种典型的多变量、强耦合非线性系统，其参数变动、时滞或外部扰动等都会使系统产生丰富的动力学行为，且当变动量满足一定条件，例如为持续性周期性负荷扰动时，就会产生无规则的、突发性的混沌现象[5-6].在电网的运行过程中，混沌现象会引起过电压、过电流，严重时会诱发电网解列、造成电压崩溃，严重影响电网的安全稳定运行[7-8].随着电网的不断互联，电力系统的运行环境变得更加复杂，电网中局部的混沌有可能演变为系统整体性混沌，在临界条件下，电力系统有可能从偏离平衡状态直接发展为整个系统的崩溃[9-10].

当前，我国电力工业和国民经济的飞速发展对电网的安全、可靠运行提出了更加严格的要求，电力系统的混沌控制已经成为国内外学者的研究热点，目前已有的混沌控制的方法有自适应控制[11]、反馈控制[12]、滑模控制[13-14]等，其中，滑模控制具有响应迅速、对扰动敏感性低、实现简单等优点，因而比其他控制方法更多地应用于电力系统的混沌控制中.文献[15]通过对具有两个不确定参数的互联电力系统混沌行为的研究，设计了基于模糊控制器的滑模控制，解决了互联混沌电力系统的控制问题；文献[16]在确认互联电力系统存在混沌现象的基础上，设计了一种反演滑模变控制法，有效地控制了系统的混沌振荡，并具有较强的鲁棒性.

在对电力系统进行滑模控制时，传统的方法是选用符号函数作为滑动控制律，然而，由于符号函数本身的跳跃性，极易导致控制过程中出现严重的抖振现象.为了避免抖振现象对电力系统造成二次破坏，文献[17]在控制过程中选取双曲函数作为滑动控制律，文献[18]采用继电特性函数代替符号函数，文献[19]运用“小误差大增益，大误差小增益”的工程特性，建立了一种特殊免疫函数，这些措施均在不同程度上减轻了滑模控制中的抖振现象.

本文在以上研究的基础上，基于含有扰动项的四阶电力系统模型，首先使用相图、Lyapunov指数谱及分叉图分析了参数变化对系统特性的影响，确认了使系统产生混沌现象的参数范围.然后，将一种新的非线性光滑函数作为滑模控制的滑动控制律，采用反演滑模控制方法对处于混沌运动的电力系统进行控制.最后，通过MATLAB仿真证实了所设计控制器的有效性.

1 含扰动的四阶电力系统模型

电力系统是由发电机、变电站、输配电线路和用电负荷组成的复杂大系统，根据文献[18]可知，含扰动项的四阶电力系统模型如下：

(1)

其中，

V=

式中，δ为发电机功角，ω是发电机角频率，E′为暂态电压，Efdr为励磁输入电压，V0是母线电压，V为发电机端电压，Vref为母线参考电压，Efd为励磁电压，Efd0为励磁参考电压，x，xd和x′d分别为线路、发电机及发电机暂态电抗，H为等值转动惯量，TA是励磁时间常数，d是阻尼因子，Pm是机械功率，KA为励磁调节增益，-Pecos(2πfet)sinδ表示电磁功率扰动项，Pe为扰动幅值，fe为扰动频率；Plsin(2πflt)表示负载功率扰动项，Pl为扰动幅值，fl为扰动频率.

当参数d=4，Pm=1，KA=130时，观察δ、ω、E′以及Efdr的运动状态，从图1所示的相图可以直观地看出系统存在典型的混沌吸引子，处于混沌运动状态.

2 混沌特性分析

2.1 耗散性和吸引子的存在性

对于该四阶电力系统(1)，系统的能量函数为

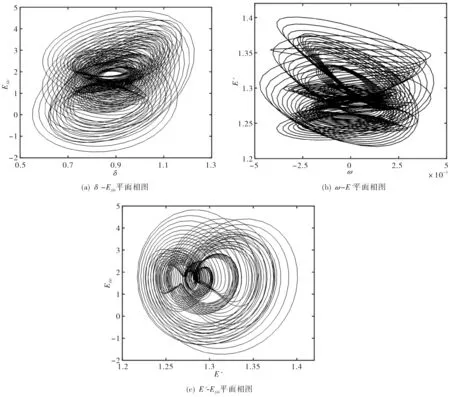
图1 四阶电力系统混沌状态相图Fig.1 State phase diagram of fourth-dimensional power system

(2)

要想确保系统(1)是耗散的，必须满足式(2)小于0，且以以下指数形式收敛：

(3)

模型中系统参数常用值如表1所示(表中各参数均为标幺值)[20].

2.2 参数变化对系统的影响性

随着参数的改变，系统平衡点的稳定性将会发

生变化，从而使系统处于不同的状态，为了更直观的体现参数d、Pm及KA变化对含扰动的电力系统的影响,令扰动项参数Pe=0.12，fe=0.2，Pl=0.08，fl=0.2，将[1.064，0，1.338，1.907]作为初始值代入分析，结果如下.

1) 固定参数d=4，Pm=1，调整KA，KA∈(70，170)时的Lyapunov指数谱如图2(a)所示，KA∈(100，140)时的分叉图如图2(b)所示.从图中可以看出，当KA∈(70，83.671)时，系统的Lyapunov指数均为负值，系统状态稳定；当KA∈(83.671，108.578)时，系统的Lyapunov指数有一个正值，三个负值，当KA∈(108.578，130.538)时，系统的Lyapunov指数有两个正值，两个负值，在这些阶段，系统出现混沌运动；当KA∈(130.538，170)时，系统的Lyapunov指数有一个正值，三个负值，此时最大Lyapunov指数值较高，初始轨道相差较大.

表1 系统参数常用值Tab.1 Common values of system parameters

图2 系统随KA变化的Lyapunov指数谱和分叉图Fig.2 Lyapunov exponent spectrum and bifurcation diagram of system with the variation of KAvalue

2)固定参数Pm=1，KA=128，调整d，d∈(0，5)时的Lyapunov指数谱如图3(a)所示，d∈(3.9，4.5)时对应的分叉图如图3(b)所示.从图中可以看出，始终存在Lyapunov指数大于0，即系统一直处于混沌运动状态；当d∈(3.543，4.412)时，系统的Lyapunov指数有两个正值，两个负值，d∈(3.543，4.051)时的最大Lyapunov指数较高，初始轨道相差较大.

3)固定参数d=4.07，KA=128，调整Pm，Pm∈(0.5，2)时的Lyapunov指数谱如图4(a)所示，Pm∈(0.95，1.05)时对应的分叉图如图4(b)所示.从图中可以看出，当Pm∈(0.5，0.924)时，系统的Lyapunov指数均为负值，系统状态稳定；当Pm∈(0.924，1.184)时，系统的Lyapunov指数有两个正值，两个负值，当Pm∈(1.184，2)时，系统的Lyapunov指数有一个正值，三个负值，在这些阶段，系统均出现混沌运动.

图3 系统随d变化的Lyapunov指数谱和分叉图Fig.3 Lyapunov exponent spectrum and bifurcation diagram of system with the variation of d value

图4 系统随Pm变化的Lyapunov指数谱和分叉图Fig.4 Lyapunov exponent spectrum and bifurcation diagram of system with the variation of Pmvalue

3 混沌行为的抑制

3.1 控制器设计及稳定性分析

对于模型(1)，以功角δ作为控制目标，添加控制器u后，得到受控系统(4).

(4)

假设1系统扰动是有界的.记电磁功率扰动项-Pecos(2πfet)sinδ为-Δe(t)，负载功率扰动项Plsin(2πflt)为Δl(t)，即存在正常数m，使得电磁功率扰动项-Δe(t)≤m；存在正常数n，使得负载功率扰动项Δl(t)≤n.

定理1对任意给定的目标函数r(t)，如果假设1成立，则在控制器(5)的作用下，系统(1)和目标函数r(t)能够实现同步，系统(1)的混沌行为被控制.

(5)

证明定义位置误差

e1=δ-r，

(6)

对式(6)求导并将式(4)代入得：

(7)

取第一个Lyapunov函数为

(8)

对(8)求导并将式(7)代入得到

(9)

令

(10)

将式(10)代入式(9)得到

(11)

取第二个Lyapunov函数为

(12)

对式(12)求导并将式(4)、式(10)、式(11)代入得：

(13)

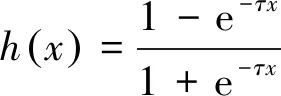
将控制器(5)代入式(13)得:

(14)

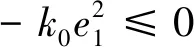
(15)

由假设1可得，-Δe(t)|≤m；Δl(t)|≤n，于是有

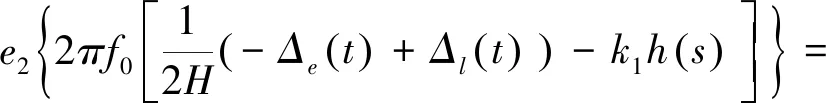
2πf0[(m+n)e2|-k1h(s)|e2|]≤

2πf0[(m+n)e2|-k1h(s)|e2|].

(16)

2πf0>0恒成立，故当k1h(s)|≥m+n时，可使得式(15)成立.

3.2 数值仿真

由上述混沌特性分析可知，当初始值为[1.064，0，1.338，1.907]，系统参数d=4.07，Pm=1.03，KA=128，扰动项参数Pe=0.12，fe=0.2，Pl=0.08，fl=0.2时，系统处于混沌状态.此时，选择控制器参数k0=5，k1=5，τ=200对系统进行控制.

令目标函数r(t)=0，功角δ的状态随时间的变化的曲线如图5(a)所示，功角δ的状态与参考信号之间的误差变量e1随时间变化的曲线如图5(b)所示，此时，控制器u的时序曲线如图5(c)所示.

令目标函数r(t)=1.5-0.2cost，调整扰动项参数为Pe=0.1，fe=0.2，Pl=0.1，fl=0.2，其余参数不变，功角δ的状态随时间的变化的曲线如图6(a)所示，功角δ的状态与参考信号之间的误差变量e1随时间变化的曲线如图6(b)所示，此时，控制器u的时序曲线如图6(c)所示.

由仿真结果可知，加入控制器后，功角δ可以迅速同步于目标函数r(t)并保持稳定，误差信号经过短时间的振荡后衰减到零，系统几乎没有抖振.

4 结论

本文针对含扰动项的四阶电力系统，利用Lyapunov指数谱及分叉图研究了阻尼因子、机械功率及励磁调节增益变化对系统状态的影响，其中，任意参数的微小变动都可能导致该四阶电力系统进入混沌状态.采用一种新的非线性光滑函数作为滑动控制律进行控制器设计，对系统进行反演滑模控制，选取不同的函数方程作为控制目标，实验仿真结果证明了本文控制方法的有效性.

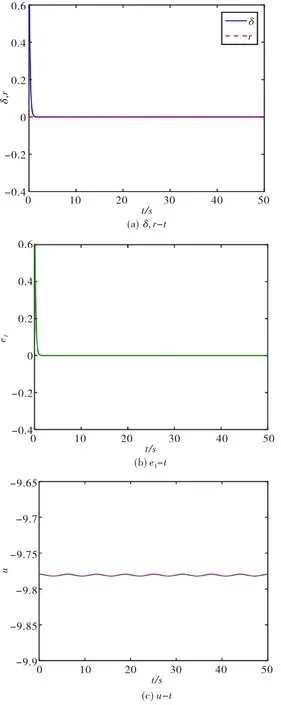
图5 目标函数为r(t)=0的滑模控制效果图Fig.5 Effect diagram of sliding mode control with objective function r(t)=0

图6 目标函数为r(t)=1.5-0.2cos t的滑模控制效果图Fig.6 Effect diagram of sliding mode control with objective function r(t)=1.5-0.2cos t