基于灰色理论与BP神经网络瓦斯涌出量预测研究
黄凯波,朱权洁,张尔辉
(华北科技学院 安全工程学院,北京 东燕郊 065201)
0 引言
煤炭是我国重要能源之一。近年来,随着煤矿开采深度的不断增加,矿井灾害频发,矿井瓦斯灾害作为矿井安全生产的主要灾害之一,长期以来严重威胁着矿工的生命安全,给国家和社会带来巨大的经济损失[1]。瓦斯是储存在煤层中的一种与煤伴生的气体,是以甲烷CH4为主的有毒、有害气体的总称,是各种气体的混合物。煤矿瓦斯是一种无色无味、易燃易爆的气体,在煤矿开采过程中,瓦斯气体从煤层中涌出,具有燃烧爆炸和突出的危险。煤矿瓦斯的主要危害形式有瓦斯窒息、瓦斯燃烧、瓦斯爆炸、瓦斯爆炸引起的煤尘爆炸或火灾等。近年来我国的煤矿瓦斯死亡事故呈现出事故危害大、重特大事故比例高,绝大多数是由于瓦斯爆炸造成的,这种事故一旦发生一次死亡人数基本在10人以上。煤矿瓦斯突出及瓦斯爆炸事故频发,严重影响了矿井的安全生产,对人身健康造成了极大的负面影响,严重限制了煤矿的生产进度。如何有效地防止瓦斯爆炸事故的发生,对煤矿的安全生产具有重要意义[2]。对煤矿瓦斯涌出量进行精准动态预测能够有效防止瓦斯灾害事故的发生[3],如何快速、有效、精准的预测瓦斯涌出量成了煤矿安全方面的一项难题。近些年来,许多国内外的学者相继对瓦斯涌出量预测做出相关研究。徐琦等[4]提出瓦斯涌出量的人工神经网络预测的研究,秦志[5]提出基于灰色理论的回采工作面瓦斯涌出量动态预测研究,张亮亮等[6]提出基于T-S模糊神经网络的瓦斯涌出量预测,贾花萍[7]提出灰色Elman神经网络的矿井瓦斯涌出量预测,张水等[8]提出瓦斯涌出量灰色-RBF网络模型的建立与应用,崔义强等[9]提出基于GA-GRNN的瓦斯涌出量预测,这些方法存在着精确度不够高,预测时间长,预测速度慢的问题。为解决上述问题,杨艳国等[10]采用多重分形理论,研究了钻屑量、钻屑解吸指数和不同孔深的特征参数对煤矿瓦斯突出事故的影响。朱志洁等[11]引入了PCA法,建立了PCA-BP煤与瓦斯突出预测模型。郭德勇等[12]应用物元和可拓集合理论建立了煤与瓦斯突出危险性预测的物元可拓模型。张子戌等[13]利用成熟的模糊理论和技术,提出了一种预测煤与瓦斯突出区域的模糊模式识别方法。温廷新等[14]提出了一种基于灰色关联熵的煤与瓦斯突出概率神经网络预测模型。这些方法并不能非常有效的预测瓦斯涌出,瓦斯涌出的影响因素非常多,因素与因素的之间存在着非常复杂的非线性关系,因此需要寻找一种能描述非线性的方法来预测瓦斯涌出量。
在现有的技术方法无法完全准确监测瓦斯涌出量的情况下,将成本更低、手段更先进、可靠性更强的灰色理论、人工神经网络相结合的方法引入到实际瓦斯涌出量监测当中,对于解决瓦斯涌出量变化的非线性问题、提高监测精度具有非常重要的现实意义。
1 灰色理论
灰色理论提出了对各个因素进行灰色关联度分析的概念,通过一定的方法,寻求系统中母因素和各个因素之间的数值关系。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,二者关联程度较高;反之,则较低。因此,灰色关联分析方法是根据因素之间发展趋势的相似或相异程度作为衡量因素间关联程度的一种方法[15]。
Step1:对X(0)作1-AGO,得序列
X(1)=(x(1)(1),x(1)(2),x(1)(3)…x(1)(n))
(1)
Step2:对X(0)作准光滑性检验。
(2)
当ρ(k)<0.5时,满足准光滑条件。
Step3:检验X(1)是否具有准指数规律。
(3)
Step4:对X(1)作紧邻均值生成。
Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))
(4)
于是
(5)
(6)
Step6:确定模型
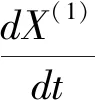
(7)
及时间响应式
(8)
Step7:求X(1)的模拟值
(9)
Step8:还原求出X(0)的模拟值:
(10)
Step9:检验误差残差:
(11)
相对误差:
(12)
残差平方和:
s=εT·ε
(13)
平均相对误差:
(14)
2 BP神经网络
BP神经网络是一种带导师的学习算法,是一种信号正向计算和误差反传的学习过程[16],其网络结构包括输入层、隐含层和输出层。在正向传播时,来自输入层的输入样本通过每一个隐含层逐层处理,然后传输到网络输出层。如果在输出层没有获得所需的输出,则将误差的反向传播,此时,误差信号从输出层传输到输入层,并一路调整各层的连接阈值和权值,使误差不断减小,直至达到目标精度[17]。
训练一个BP神经网络,可先计算网络加权输入矢量以及网络输出和误差矢量,然后求得误差平方和。当所训练矢量的误差平方和小于误差目标,则训练停止;否则,在输出层计算误差变化,采用逆向转播学习规则来调权值,并不断重复此过程。当网络完成训练后,最后以泛方式给出输出结果
其建模过程如下:
第一步,网络初始化,给各连接权值分别赋一个区间(-1,1)内的随机数,设定误差函数e,给定计算精度值ε和最大学习次数M。
第二步,随机选取第K个输入样本及对应期望输出,其公式如下:
x(k)=(x1(k),x2(k),…,xn(k))
(15)
d0(k)=(d1(k),d2(k),…,dq(k))
(16)
第三步,计算隐含层各神经元的输入和输出,其公式如下:
(17)
(18)
(19)
(20)
第四步,利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数δo(k),其公式如下:
(21)
(22)
(23)
第五步,利用隐含层到输出层的连接权值、输出层的δo(k)和隐含层的输出计算误差函数对隐含层各神经元的偏导数δh(k):
众所周知,新课程改革倡导的是自主、合作、探究式的学习方式。新课程改革背景下的课堂教学首先强调的是学生的自主学习,只要是学生能够独立完成的学习任务,教师就不需要去花费更多的时间。反过来,只要是学生自主学习过程中没有办法解决的问题就是接下来课堂学习所要着力突破的。因此,无论学生以什么样的方式进行探究,都要强调他们的合作协同。因为这些疑难都是学生在自主学习过程中产生的,是个人的智慧所无法解决的,确实需要教师组织学生通过集体智慧加以突破。
(24)
第六步,利用输出层各神经元的δo(k)和隐含层各神经元的输出来修正连接权值who(k) ,其公式如下:
(25)
第七步,利用隐含层各神经元的δh(k)和输入层各神经元的输入修正连接权:
(26)
第八步,计算全局误差,其公式如下:
(27)
第九步,判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
3 工程实例应用
3.1 工程背景
山西某矿长期以来深受瓦斯灾害困扰,严重制约着矿井安全生产的快速落实和煤炭采出率的稳步提升。近年来,该矿已有多起瓦斯事故突发,如瓦斯爆炸、煤与瓦斯突出等,给广大职工的生命安全和财产保障带来了严重的威胁。因此,开展瓦斯涌出量预测,掌握瓦斯涌出规律,防止瓦斯灾害事故,实现矿井瓦斯灾害的提前预警已成为该矿的主要工作之一。为确保预测结果的准确性,选取该矿某一突出煤层进行现场实测,测量指标包括煤层埋藏深度、煤层厚度、煤层瓦斯含量、煤层间距、日进尺、日常量和绝对瓦斯涌出量。现场实测结果如表1所示。以表1数据为支撑,利用本文提出的灰色-BP神经网络对该矿开展瓦斯涌出量精准预测。
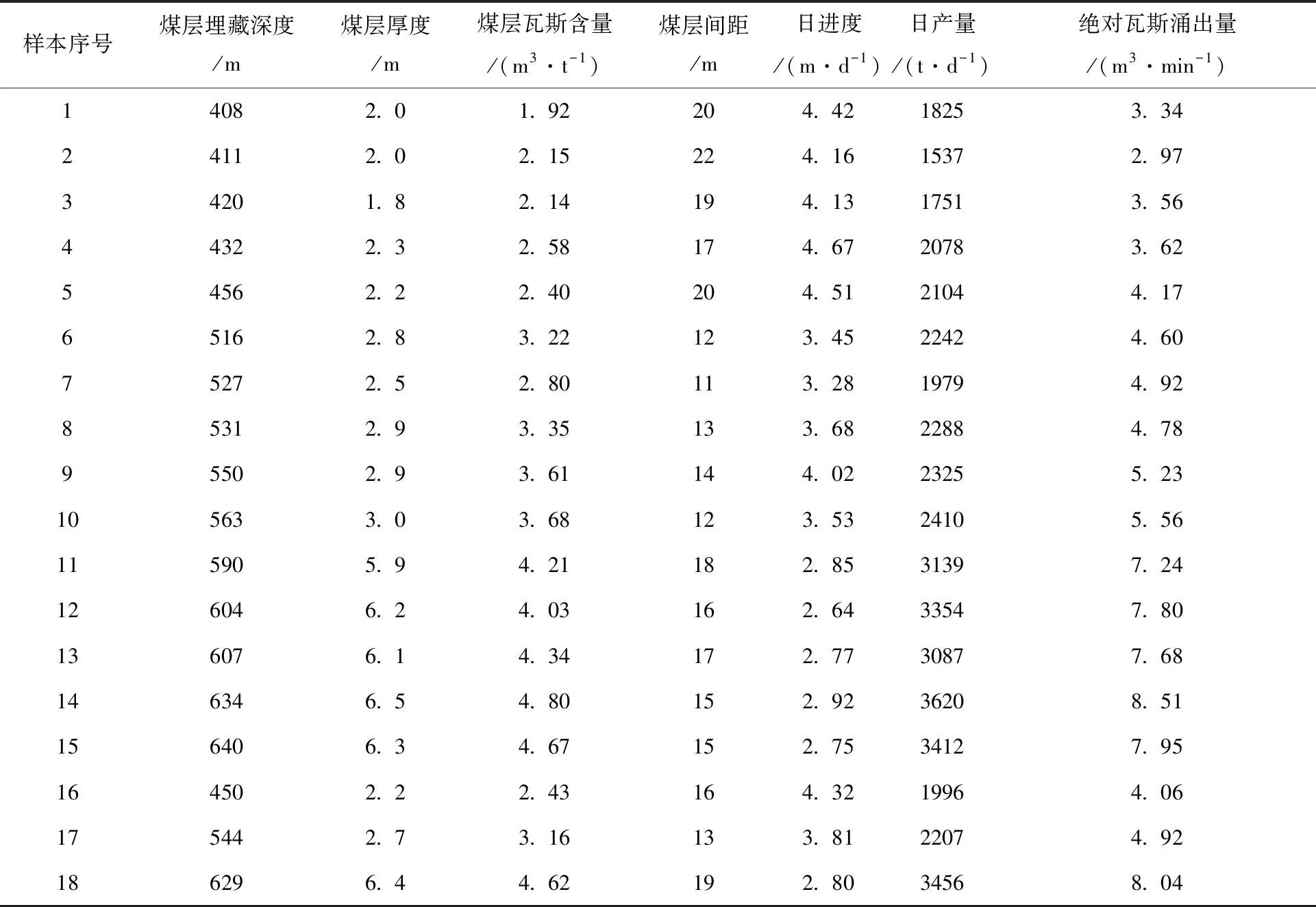
表1 观测原始数据
由上表数据并不能看出瓦斯涌出量与其影响因素之间的关系,因为数据较为离散,各特征关联性不强,利用常规的数学曲线方式无法进行预测,因此,需要借助更优的方法或预测模型进行分析。
3.2 预测模型构建
典型的BP神经网络包括输入层X,隐含层R,输出层Y进行连接。因此,可以利用人工神经网络在多输入层在瓦斯涌出产生的多方面原因做定向输入,经过复杂的计算最终得到预测数据。
本文引用实际测量数据,以此为基础,创建合格的符合预期的人工神经网络模型,以BP神经网络为例,对其进行预测。利用Matlab软件,网络参数设置训练次数为10000,训练目标为le-7,学习率为0.01,动量因子为0.9,显示间隔次数为50。
其中,BP神经元以m个输入层,m个隐含层,m个输出层组成,如图1所示。

图1 BP网络拓扑结构图
基于灰色—神经网络模型的瓦斯涌出量预测流程如下:首先,现场瓦斯数据实测,并对原始数据进行预处理,保证原始数据的准确性和统一性。其次,以实测瓦斯涌出量预测指标原始数据为基础,利用灰色预测得到初步预测值,将预测值通过BP神经网络进行修正得出修正后的预测值。再次,结合绝对瓦斯涌出量现场实测值,对比分析预测结果的准确信和有效性。最后,输出最终的预测结果,确定瓦斯涌出量规律。其流程步骤如图2所示。
本文将表1中现场实测数据作为原始数据利用灰色预测模型通过MATLAB软件进行数学运算,得到灰色预测值,再将灰色预测值反馈给已学习好的BP神经网络,通过基于BP神经网络构建的MATLAB代码得出BP预测值。将这两个值进行对比分析得出最终预测值。
3.3 结果分析
利用新的灰色—BP神经网络模型对表2中的数据进行预测,灰色理论预测结果与实际结果偏差较大,特别是其绝对值。大于20%,分别在序号为2、3、4、14、16、17;大于50%,分别在序号为16、17;其他大部分还是预测比较准确的,仅在局部出现预测不准确的情况。

图2 灰色—神经网络模型预测流程图
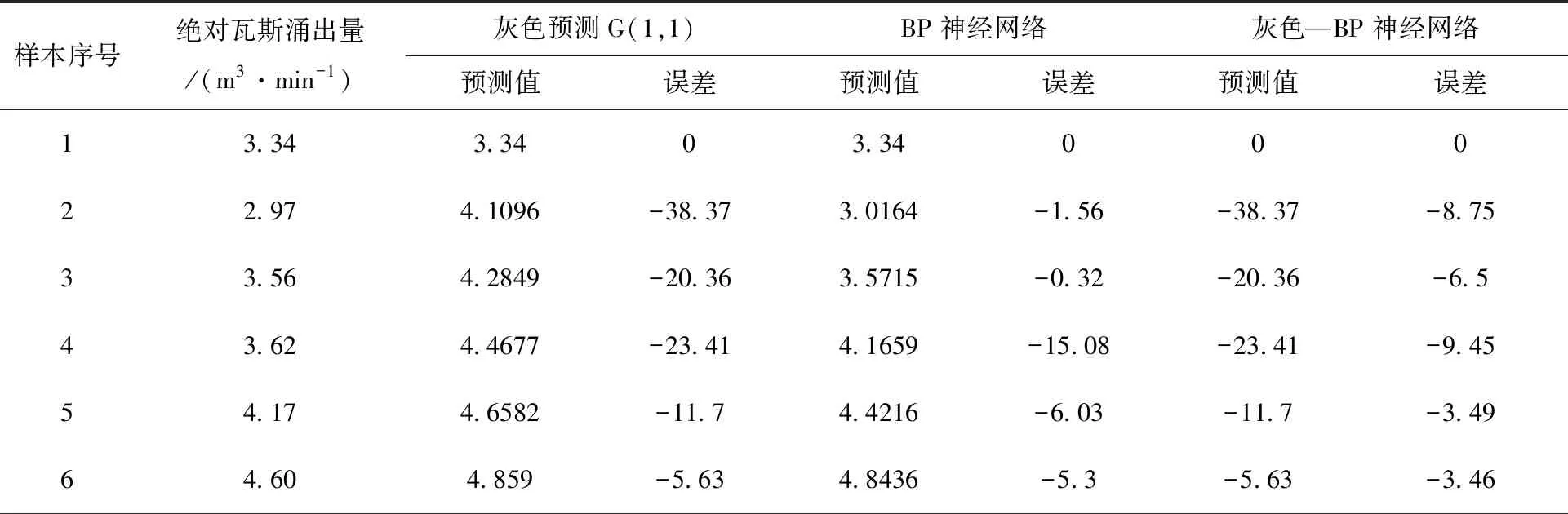
表2 数据预测对比图
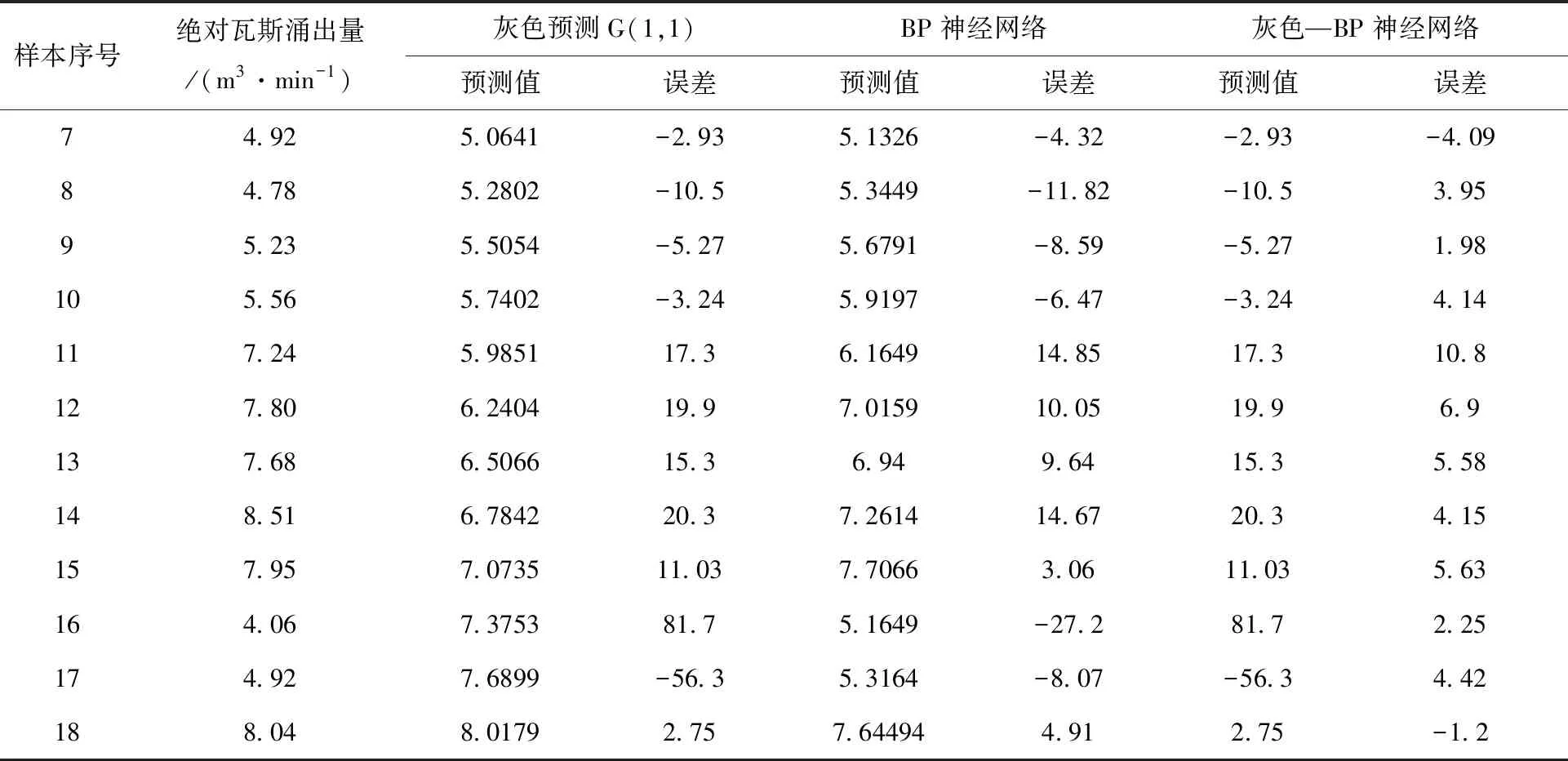
续表
将BP神经网络与灰色预测结合起来构建的灰色—BP神经网络预测模型有着很好的预测效果,与真实值得误差控制的非常小,总体上都能控制在10%以内。此外,将由原始绝对瓦斯涌出量、灰色预测模型预测值、灰色—BP神经网络模型预测值四种数据作对比,做成折线图如图3。由图3得出其灰色—BP神经网络预测值明显比其他两种预测值拟合的效果更好。在样本序号10以前灰色预测和灰色—BP神经网络预测结果和实际值相差不大,但在样本序号10以后,影响瓦斯涌出量的因素发生改变,灰色预测明显不能精准的对其进行准确的预测,但基于灰色—BP神经网络学习影响因素的变化而产生变化,使其能准确的进行预测。
图4为两种预测的误差绝对值的对比图,图中显示了灰色预测误差、BP神经网络预测误差以及灰色—BP神经网络预测误差。由图可知,灰色预测结果误差最大,且随机波动性较大,BP神经网络预测结果误差次之。灰色—BP神经网络预测误差最小,且误差波动较小,表明基于灰色—BP神经网络的瓦斯涌出量预测结果准确度有很大提高,且该方法预测结果稳定,无大幅度波动,不受人为因素和其他干扰因素的影响。
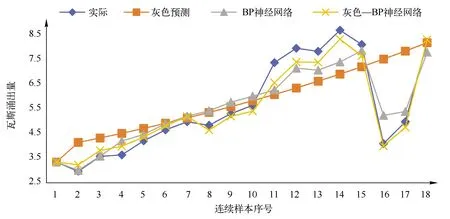
图3 对比折线图
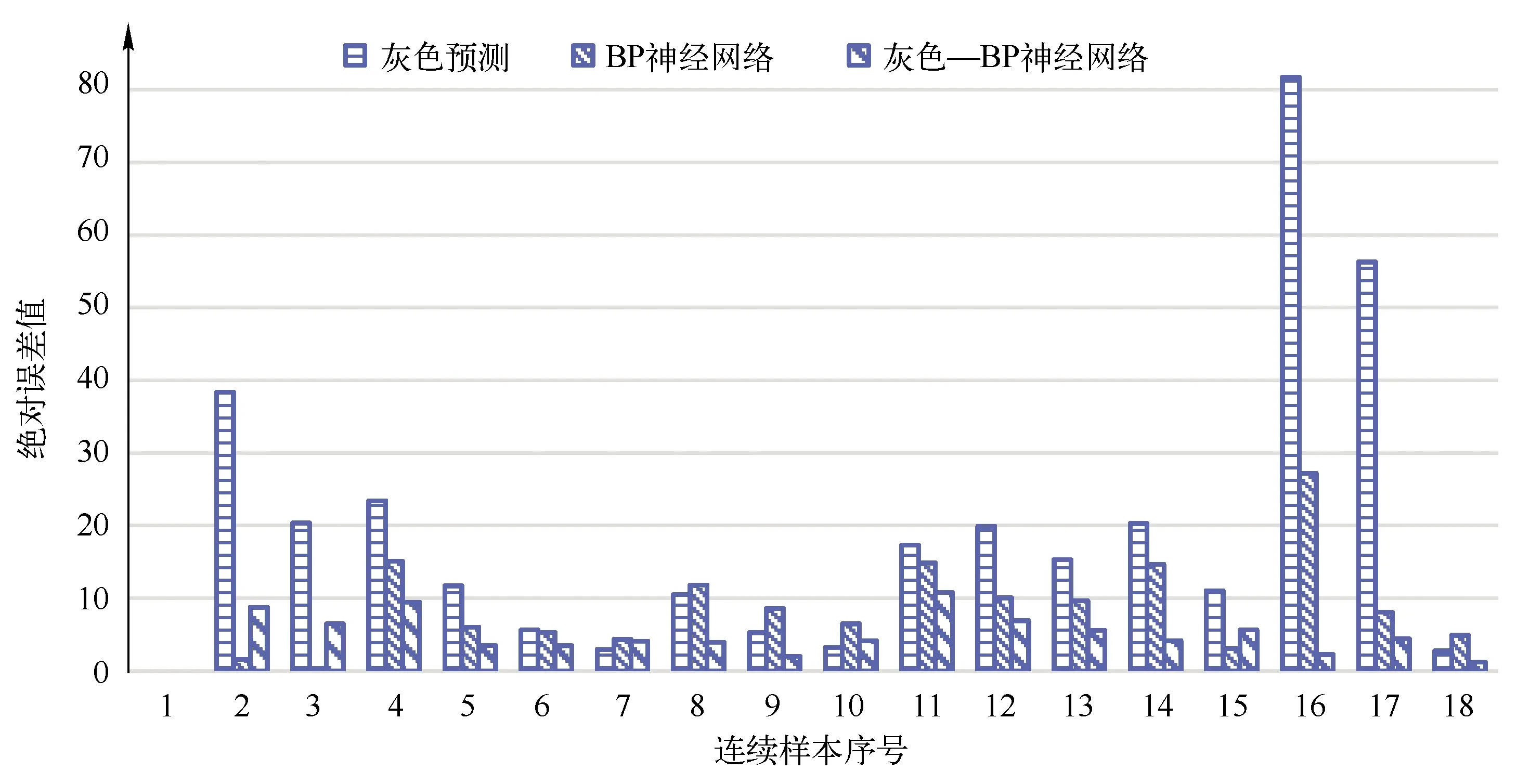
图4 误差对比图
4 结论
(1) 提出了基于灰色—BP神经网络的矿井瓦斯涌出量预测方法。确定了煤层埋藏深度、煤层厚度、煤层瓦斯含量、煤层间距、日进尺、日常量和绝对瓦斯涌出量作为瓦斯涌出量预测指标。
(2) 基于灰色—BP神经网络系统对山西某矿瓦斯涌出量进行了预测。通过对比灰色预测、BP神经网络和灰色—BP神经网络的预测结果误差。对比发现,灰色—BP神经网络预测的数据精确度和可靠性更高。由此表明灰色—BP神经网络在矿井瓦斯涌出量预测中的合理性和可行性。
(3) 鉴于灰色—BP神经网络系统在矿井瓦斯涌出量预测中的准确性和适用性,可推广应用于冲击地压、矿井突水等矿井灾害的预警中,对减低事故率,实现安全生产具有指导意义。

