基于机器学习的含植被水流流速分布研究
韩 宇,刘家备,穆 同,刘晓东,唐良川
(1.中国农业大学水利与土木工程学院,北京 100083;2.中国农业大学信息与电气工程学院,北京 100083)
植被广泛分布于天然河道中,洪水的产生,及水体生态修复都与河道中水生植被的存在有密切联系。水生植被包括淹没和非淹没两种情况,其对水流阻力,湍流特性和涡结构均造成显著影响,因此对含植被水流的研究是有必要的。近年来,含植被水流的水力特性,流速分布结构和生态效应研究受到广泛关注。本文采用机器学习及物理模型试验的方法讨论了水生植被对水流流速结构的影响。
Karman-Prandtl对数定律常被用来描述明渠竖向流速剖面。经Stephan和Gutknecht[1]修正后的速度剖面方程如下:
(1)
(2)
式中:u是顺水流的时均流速;u*是摩阻流速;κ是卡门常数;z是纵坐标;ks是等效砂粒粗糙度;C是积分常数;he是有效植株高度。
虽然,式(1)和(2)可以较好地描述渠道竖向流速分布,但不利于估计河道过流流量。Chezy和Manning公式广泛运用于估算渠道流速和流量:
(3)
(4)
式中:v是平均流速;Q是平均流量;A是过水断面面积;R是水力半径;S是水力梯度;n是Manning粗糙系数。
n的值由实验数据估算得到,这导致该值可能不精确[2]。此外,这些阻力系数不是专门为含植被河道选取的,所以在应用时它们的值往往会被低估[3]。水生植被对水流阻力具有显著影响,由圆柱绕流理论[4]可得:
(5)
式中:F为拖曳力;CD为拖曳力系数;Av为圆柱迎水面积;ρ为水黏度;U为平均纵向流速。
进一步的研究发现植被特征对水流结构有显著影响。植被孔隙度和柔韧性的降低可能会导致过渡层高的减小[5]。模拟实验表明,植被的密度和排列方式在一定程度上影响流速,阻力随着密度的增加而增大[6]。虽然平均流速可能随着植被密度的增加而减小,但湍流强度可能保持不变,甚至会增加[7]。此外,植被的长度、高度和柔韧性对水流结构的影响也存在不同[8]。
数值模拟是一种揭示水流结构与植被关系常规而有效的方法。其中最典型的是RANS模型和LES模型。RANS模型由一个或多个描述湍流各向异性的方程组成[9]。LES模型则是最近才发展起来,槐文信等[10]利用该模型研究了非淹没植被下的明渠水流。与RANS模型相比,LES模型使用的网格数是前者的100多倍,限制了其在实际中的应用。但是LES模型可以提供更多关于三维湍流场和雷诺应力的信息。并且由LES模型计算的速度和雷诺剪切应力的垂直分布比RANS模型的计算结果更加合理。RANS模型反映了流体的质量守恒和动量守恒:
(6)
(7)
式中:xi(=x,y,z)分别为顺水流、指向侧壁和垂直水面的坐标轴方向;ui(=u,v,w)分别为x,y,z方向的时均速度分量;t是时间;vm是分子黏度;vs是网格尺度黏度;ρ是液体密度;p是静态压降;Fi(=Fx,Fy,Fz)为每单位体积内沿x,y,z方向的阻力分量;gi=(0,0,-9.8 m/s2)为重力加速度。
虽然RANS模型在数值模拟中得到了广泛应用,但它的一个缺点是控制方程依赖网格的划分精度,求解的收敛性较差。为了克服这个困难,常用LES方法对其进行局部修正。近年来,通过数值模拟得到了大量有用的结果。王超等[11]采用深度平均的二维水动力模型模拟了南四湖植被带和非植被带的流场。槐文信等[12]应用混合掺长法,根据Karman相似理论改进了混合长度的表达,分析了含淹没和非淹没刚性植被的水流结构。他们将植被淹没情况下的水流结构划分为四个区域,而将植被非淹没情况下的水流结构分成了二个区域。王沛芳等[13]利用三维水动力模型预测了浅水湖泊淹没植被区水平速度的垂直分布。
目前大部分经验公式和数值计算都来自对处于特定工况下特定类型植被的研究,试验历时长、经费投入大,引入机器学习的方法可以提高实测数据的利用效率,使结果在工程应用中更容易被获得。机器学习能对具有一定内在关系的数据进行自适应建模,已在自然语言处理、计算机图像识别等领域取得了巨大的成功,在水力学的相关领域亦表现不凡。Azamathulla等[14]利用基因编程,以水力半径、特征粒径和底坡为自变量建立的高梯度水流中曼宁粗糙系数的预测模型要优于传统的经验公式。Ghani等[15]基于遗传规划推导的天然河流纵向扩散系数的表达式包含了河宽、水深等几何参数和平均剪切速度等水力参数,该表达式应用于宽幅河流时性能良好。Alexander等[16]将高斯回归分析引入到径流的概率预测中,开发了一种层次化的贝叶斯框架,用于推断河流流量的后验分布。顾峰等[17]通过随机森林优选后的特征变量对研究区内的湿地信息进行提取,提高了运行的准确性和效率。
本文的研究目的是将机器学习的方法引入到含植被水流断面流速的建模和预测中,使用四种不同的机器学习方法分析含植被明渠的流速分布,以物理模型试验得到的实测数据为训练集,分别建立数据驱动型模型,通过模型计算值与实际测量值间的比较评估每种模型的性能,确定最适合预测含植被明渠流速分布的机器学习模型。
1 模型介绍
1.1 神经网络
BP神经网络是一种多层前馈神经网络,由Werbos[18]在1974年首次提出。Hornik等[19]在1989年证明了多层前馈神经网络只需要一个有足够数量神经元的隐含层就能以任意精度逼近任意复杂的连续函数。该网络的主要特点是信号前向传递,误差反向传播。在前向传递中,输入信号从输入层经隐含层逐层处理,直至输出层。每一层的神经元状态仅影响下一层的神经元状态。如果输出层得不到期望输出,则转反向传播,根据预测误差调整网络权值和阈值,从而使BP神经网络预测输出不断逼近期望输出。BP神经网络的拓扑结构如图1所示。
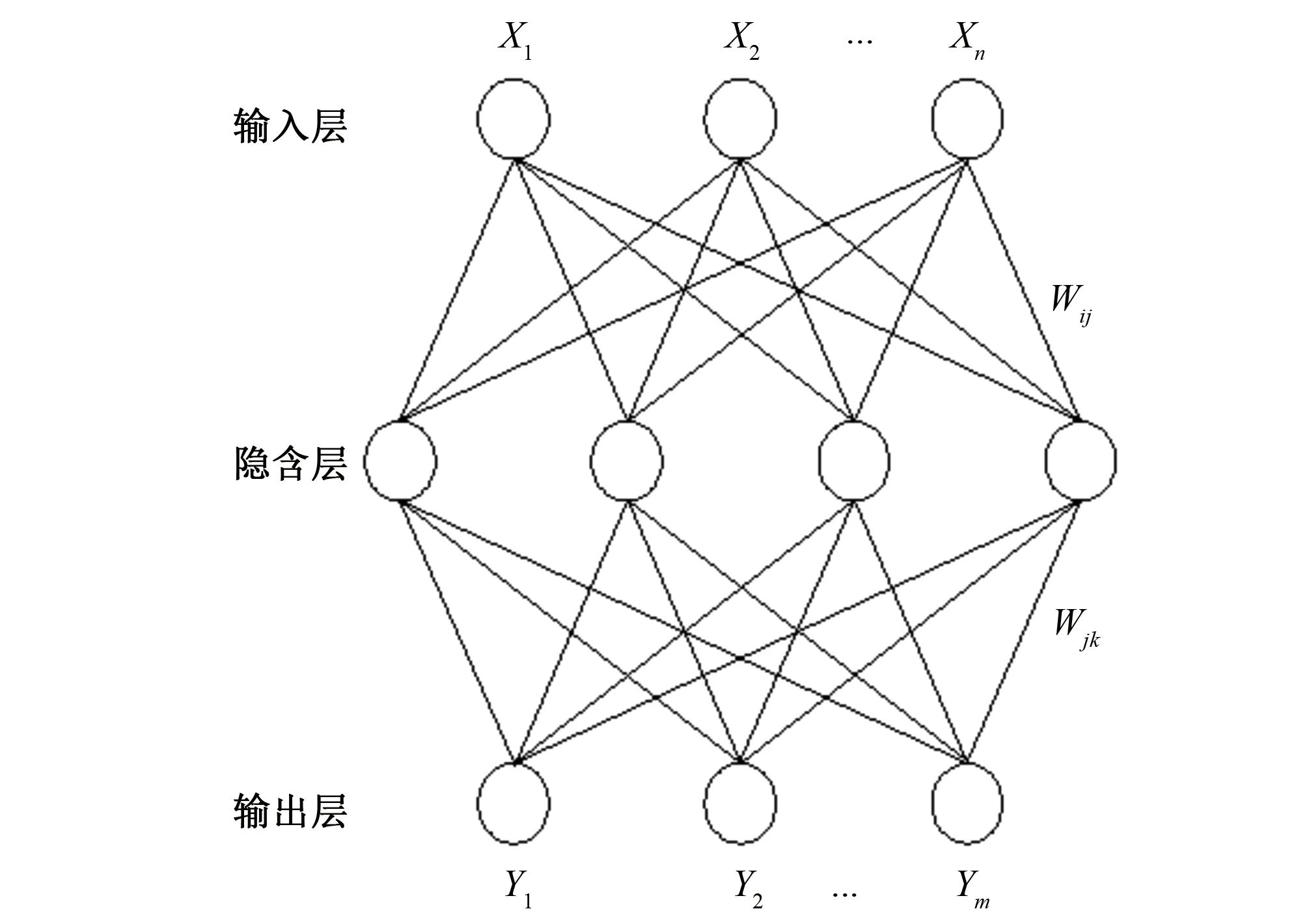
图1 BP神经网络的拓扑结构图Fig.1 Topology diagram of BP neural network
图1中X1,X2,…,Xn是BP神经网络的输入值,Y1,Y2,…,Ym是BP神经网络的预测值,Wij和Wjk为BP神经网络的权值。从结构图中可以看出,BP神经网络可以看成一个非线性函数,网络输入值和预测值分别为该函数的自变量和因变量。当输入节点数为n、输出节点数为m时,BP神经网络就表达了从n个自变量到m个因变量的函数映射关系。BP神经网络要通过训练使网络具有联想记忆和预测能力。
1.2 支持向量回归SVR
支持向量机由Cortes等[20]首先提出,常用于模式分类和非线性回归。对于一个给定的样本集D={(x1,y1),(x2,y2),…,(xm,ym)},求它的回归曲线就是要找到一条曲线f(x)=wTx+b使其预测值f(x)与真实值y尽可能相近,w和b是待定的参数。在支持向量回归SVR中,容许f(x)与y最多相差ε,即|f(x)-y|≤ε时,近似认为误差为0。这样就相当于在f(x)上下构造了一条宽度为2ε的间隔带,在此间隔带内的预测都是正确的。由此可得到SVR的基础形式:
(8)
式中:C为正则化项;lε为损失函数,
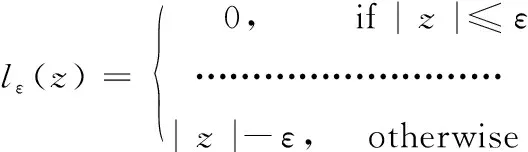
(9)
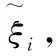
(10)
至此,SVR转化为了一个最优化问题。当优化问题存在不等式约束时,常使用拉格朗日乘子法与KKT条件进行求解。同时为便于后续处理,进一步将其转化为对偶问题,最终解得一个线性的回归函数。若要获得更复杂的非线性回归函数,还需引入核函数进行映射。
1.3 RBF神经网络
RBF径向基函数网络是一种单隐含层前馈神经网络,由Broomhead等[21]在1988提出。理论上可使用多个隐含层,但一般将RBF设置为单隐含层。它使用径向基函数作为隐含层的神经元激活函数,而输出层则是关于隐含层神经元输出的线性组合。RBF的本质是把以低维模式输入的数据变换到高维空间中,然后使在低维空间内线性不可分的数据集合在高维空间内实现线性可分。1991年,Park等[22]证明了RBF网络只要包含足够多的隐含层神经元,便能以任意精度逼近任意连续函数。RBF神经网络可表示为:

(11)
式中:x为输入向量;q为隐含层神经元的个数;wi和ci分别为第i个隐含层神经元的权值和中心;ρ(x,ci)是径向基函数,它是关于中心点径向对称且衰减的非负非线性标量函数。常用的高斯径向基函数为:
ρ(x,ci)=e-βi‖x-ci‖2
(12)
式中:βi为模型待定的参数。
1.4 随机森林RF
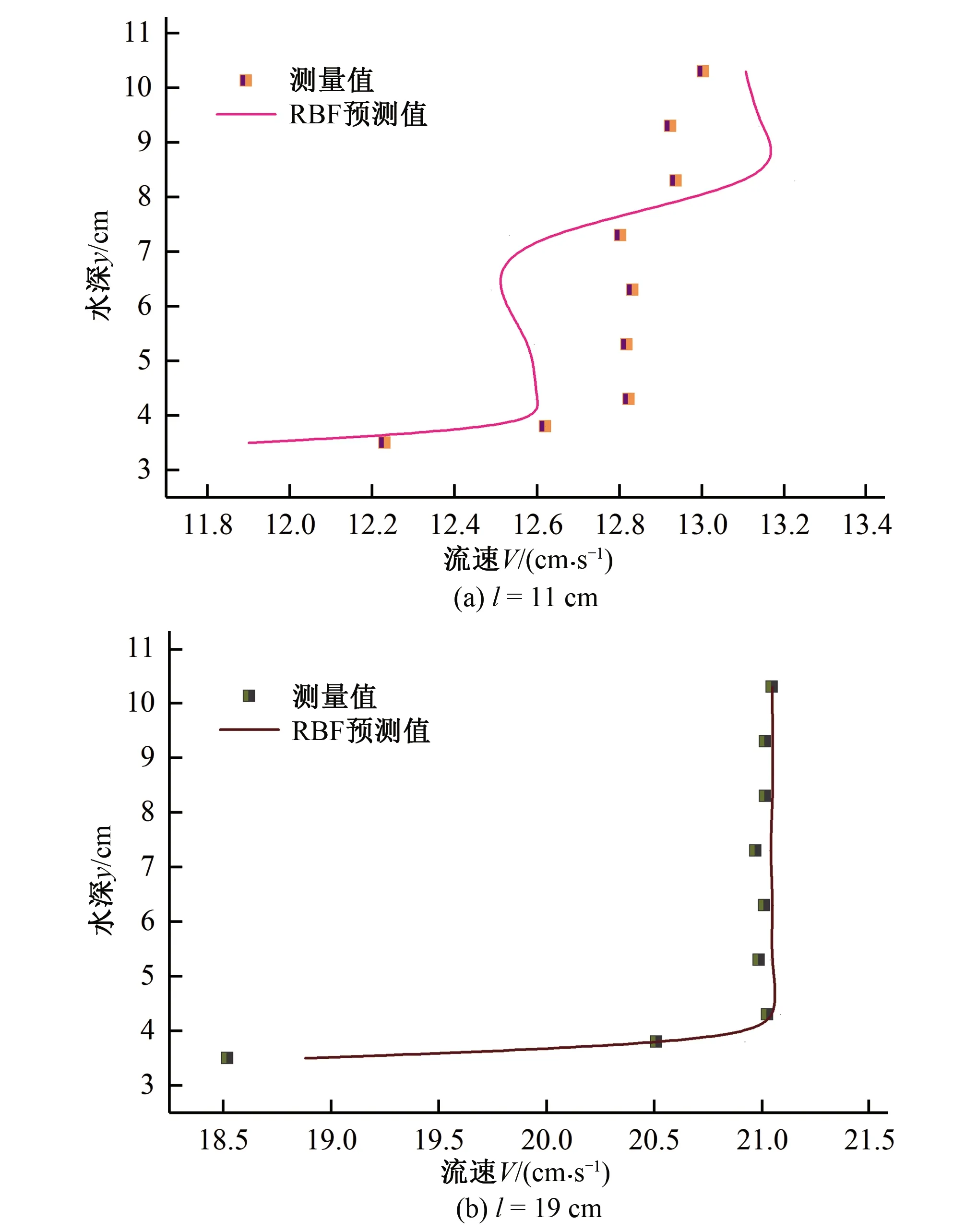
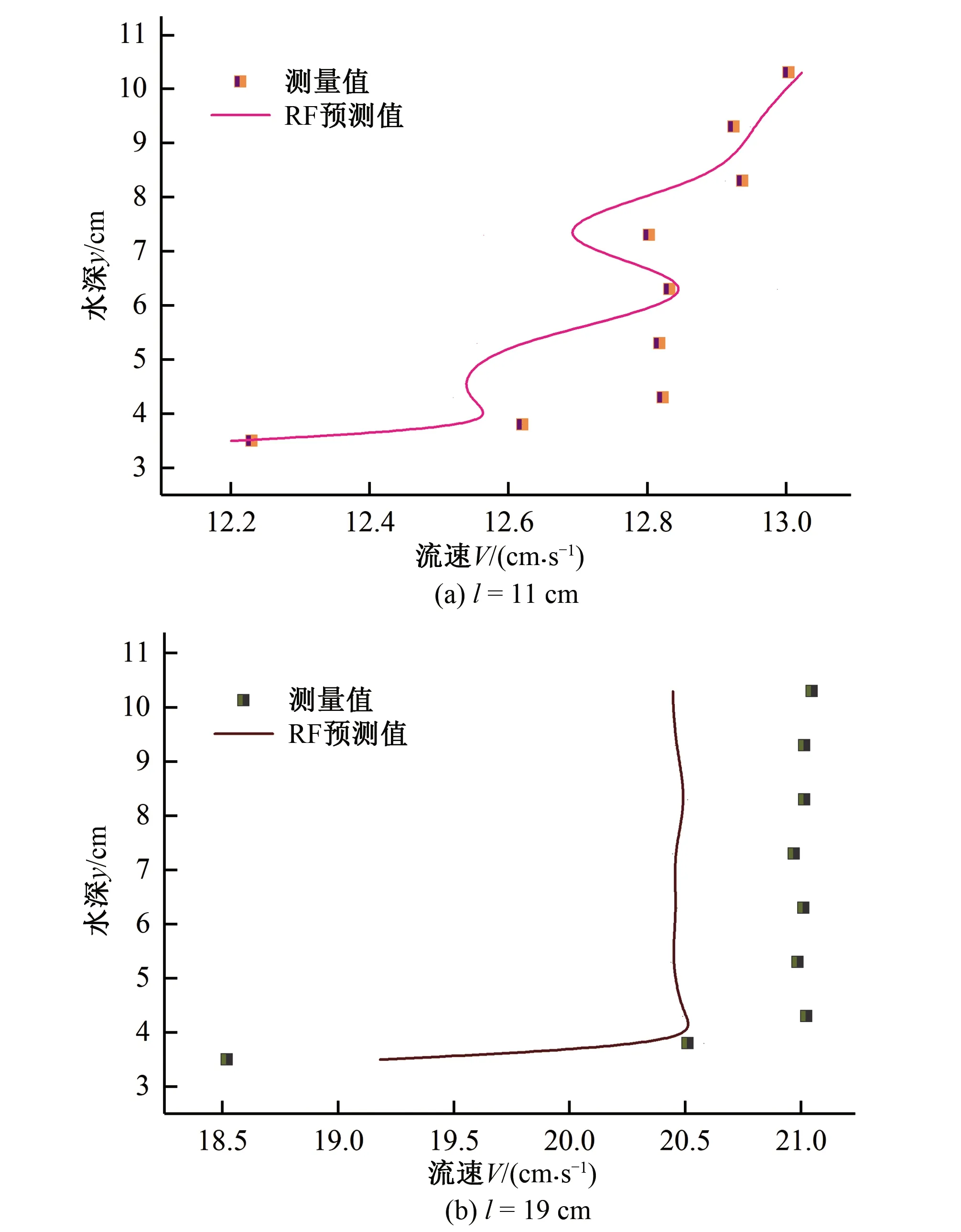
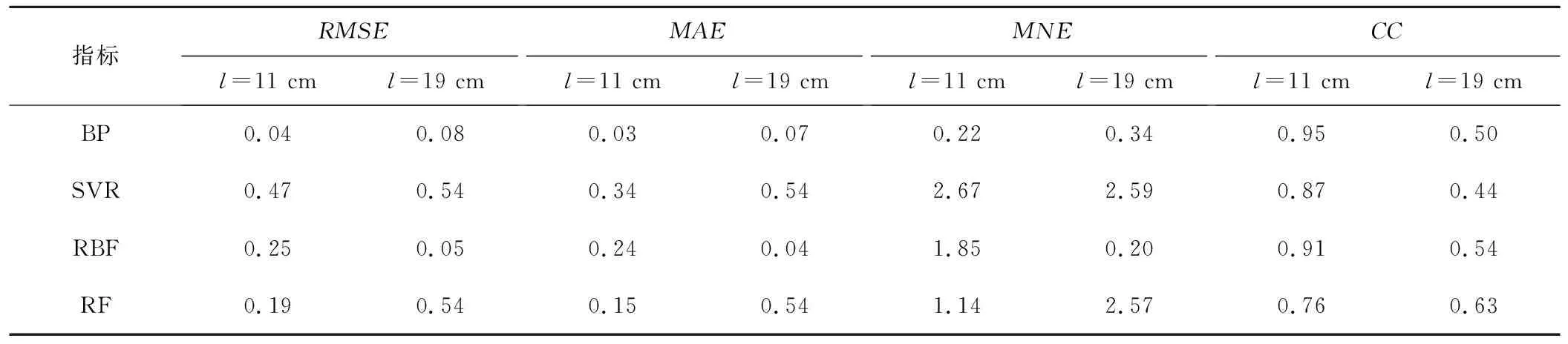
2001年,Breiman[23]在随机子空间的指导思想下提出了随机森林算法,并从理论和实践两个层面系统地阐述了该算法。自此随机森林算法得到迅速应用,被誉为“代表集成学习技术水平的方法”。随机森林本质上是由多个决策树组成的分类器,当其用于回归时,取每棵决策树结果的平均值作为最后预测的结果。随机森林实现过程是这样的:对于每一棵树,都从N个训练样本中随机且有放回地抽取n(n 本试验在中国农业大学水利与土木工程学院的水力试验大厅进行,试验水槽主要由测流装置、控制装置、供水及循环装置三部分组成。其中测流装置主要包括三维超声波多普勒流速仪(ADV)、电磁流量计和测压管;控制装置由尾门、稳流蜂巢、变频器等组成;供水及循环装置包括储水池、进水箱,玻璃水槽和循环管道等。试验装置布置图如图2所示。 图2 试验装置布置图Fig.2 Layout of test equipment 主体水槽长6.3 m、宽0.8 m、高0.6 m。两边为玻璃壁面,在中间距进水口0.5 m处放置长5.3 m、宽0.8 m、厚0.01 m的硬质塑料底板。在底板上以梅花状布置横向和纵向间距均为0.06 m的插孔。水流通过渠首的进水阀门,经过稳流蜂巢充分紊动消能,稳定后以接近均匀流的流态进入水槽。尾水箱处设有尾门,旋转把手调节尾门的相对开度可以控制水槽的水位。水槽的水深则由安装在水槽一侧的测压管读出。流量大小可通过变频控制器调节,由电磁流量计直接读出,可与测量流量进行比对校核。 无论是刚性还是柔性的天然水生植物,其自然特性复杂且不易固定,不适合直接用于测量试验。本试验采用高0.3 m、直径为0.005 m的亚克力有机玻璃棒来模拟非淹没刚性植物。图3为渠道试验实景图。该试验以植被的排数、间距和水流流速为试验变量,不同试验工况汇总于表1。Q是流量,H是对应的水深。 图3 渠道试验实景图Fig.3 Channel experiment scene map 表1 试验工况汇总 试验工况植被间距/m植被排数Q/(m3·h-1) H/m D10.061700.0900.061800.0990.061900.1060.0611000.1140.0611100.1210.0611200.128D20.181~270~1200.090~0.128D30.301~270~1200.090~0.128 流速的测量采用三维超声波多普勒流速仪(ADV),将其安装于水槽上方可以横纵移动的导轨上,设置采样频率为25 Hz,量程为0.5 m,每处测点的采样时间为3 min,每单点采集瞬时值约为3 000个。Takemurat等[24]在研究含植被河道的水力特征时发现测点的位置是一个非常重要的影响因素,且ADV是单点测速,故本试验采用渠道中部流速测量结果来近似代表整体植被群对水流流速作用的平均水平。又因植株对水流存在扰动作用,植被内部的流场时空分布不均,同一测点在不同时刻测得的流速变化范围较大,根据ADV的测量特点,对一处测点多次测得的瞬时值进行时均处理。 将试验得到的数据整理如表2。表2中Q(m3/h)是流量,l(cm)为测点沿流向距亚克力棒的纵向距离,y(cm)测点距槽底的垂直距离,V(cm/s)是速度时均值。 表2 试验数据集的统计参数Tab.2 Statistical parameters of the test data set 注:负号表示与正向相反。 以Q,l,y为输入参变量,V为输出参变量,构成机器学映射关系f。 V=f(Q,l,y) (13) 采取分层抽样的方式,把数据集的80%用于机器学习模型的训练,余下的20%,一半用于检验,一半用于测试。在对BP神经网络和RBF神经网络进行训练前,原始数据需进行归一化处理,把所有数据都转化为[0,1]之间的数。归一化的目的是消除数据间数量级的差别,避免因数据量级差别较大而造成误差的积累;并去掉各项特征指标的量纲,便于综合比较;同时可以加快求解的收敛速度,提高模型的精度。支持向量回归SVR本身具有正交最小二乘优选的属性,不需要对样本数据进行训练,但使用经过归一化处理后的数据可以显著减小其输出结果的均方根误差(RMSE)。是否对数据集进行归一化处理对随机森林RF的影响不大。综上,对4个模型都使用归一化后的数据。在本文中,数据归一化采用最大最小法处理: (14) 式中:x′为归一化后的数据;x为原始数据;xmin为原始数据序列中的最小值;xmax为原始数据序列中的最大值。 为了反映模型的训练情况,将流速V(cm/s)的测量值与模拟值进行一次线性相关分析,并计算两者的一次线性拟合函数和相关系数的平方R2,结果如图4至图7所示。图中竖轴y和横轴x分别代表流速V(cm/s)的模拟值和测量值。 图4 BP不同数据集的相关系数Fig.4 Correlation coefficients of BP data sets 图5 SVR不同数据集的相关系数Fig.5 Correlation coefficients of SVR data sets 图6 RBF不同数据集的相关系数Fig.6 Correlation coefficients of RBF data sets 图7 RF不同数据集的相关系数Fig.7 Correlation coefficients of RF data sets 测量值与模拟值一次拟合直线的斜率越接近1,相关系数越大,表明两者的差别越小,即模型的训练效果和测试效果越好。由上图可知,效果最好的是BP神经网络,其训练集模拟值与测量值间的相关系数达到了0.95,验证集达到了0.98,测试集达到了0.98,全集(所有数据)计算获得的模拟值与测量值间的相关系数达到了0.95。需要注意的是,验证集、测试集的样本容量和训练集、全集的样本容量相比较小,且数据集具体的划分选取有不同,导致它们之间拟合直线的斜率和相关系数存在一定差异,这一点在由SVR模型计算出的结果中尤为明显:测试集和验证集的相关系数分别达到了0.90和0.94,而训练集和全集的相关系数分别只有0.74和0.76。这说明了SVR模型在全局和局部上的模拟能力具有差别。 为验证机器学习模型的正确性,将Q=160 m3/s,l分别等于11 cm,19 cm时的计算结果与试验测量值进行对比,结果如图8至11所示。 图8 BP模型预测结果与试验结果对比Fig.8 Comparison of velocity values between prediction and measurement using BP 图9 SVR模型预测结果与试验结果对比Fig.9 Comparison of velocity values between prediction and measurement using SVR 图10 RBF模型预测结果与试验结果对比Fig.10 Comparison of velocity values between prediction and measurement using RBF 图11 RF模型预测结果与试验结果对比Fig.11 Comparison of velocity values between prediction and measurement using RF 根据图8至11结果显示,对应相同的l值,由不同模型计算出的V值与测量值的拟合程度存在明显差异。l=11 cm时,BP的预测值与测量值吻合良好,其余模型都存在局部失真的情况。l=19 cm时,BP和RBF的预测值除了在y=3 cm附近比实际值大,以上水深区域都与实际值拟合较好,而SVR的结果普遍偏大,RF则整体偏小。误差的来源主要有两个方面,一是用来训练和学习的数据集,二是每个模型内在的算法原理。BP神经网络是一个全局收敛和局本搜索优化的算法,具有很强的容错能力和泛化能力,部分神经元受到数据扰动的破坏不会对全局的训练结果造成很大影响,经过训练后的网络对新的或有噪声污染的数据依然能够进行正确的处理,所以BP整体的误差较小。SVR算法的核心是将低维数据集在高维空间内用超平面进行划分,使尽可能多的数据点到分划超平面的距离最近,但其不能保证所有的数据点都达到理想的位置,尤其是在本文样本容量大的情况下,更容易出现欠拟合的现象,进而导致误差过大。RBF性能的表现依赖于初始样本中心的选取,受病态数据干扰的影响较大。l越大,即距亚克力棒越远,流速值测量的结果受棒后涡动区的影响就越小,病态数据也越少,所以从图10可以看出,l=19 cm时的误差要比l=11 cm时的误差小很多。RF模型的误差主要源于数据本身,因为实验中难以保证在紊动强烈区所测数据的质量,所以使得RF的预测值与测量值相比偏差较大,并且这种误差不会随着决策树设置的多少而得到显著的降低。综上,提高训练数据的质量并合理选取机器学习的模型是确保预测结果可信度的有效方法。 引入以下统计指标,对4种机器学习模型进行综合评价。 均方根误差(RMSE): (15) 平均绝对误差(MAE): (16) 规范均方差(MNE): (17) 相关系数(CC): (18) 4个模型的RMSE值、MAE值、MNE值和CC值如表3所示。 表3 模型的统计指标评价Tab.3 Statistical index evaluation of the models 为了对各模型的性能做出综合评价,此处采用模糊数学中模糊意见集中决策的方法[25]:设论域U={u1,u2,…,un},将U中元素进行排序。有专家组|M|=m人,发表m种意见,记为V={v1,v2,…,vm}。其中vi是第i种意见序列,即U中元素的某一个排序。令u∈U,定义Bi(u)表示第i种意见序列vi中排在u之后的元素个数,若u在第i种意见序列vi中排在第k位,则Bi(u)=n-k。称为u的Borda数。论域U的所有元素可按Borda数的大小排序,Borda数越大,评价越高。现以RMSE值、MAE值、MNE值和CC值为意见指标,列表4计算各模型的Borda数。 (19) 表4 模型的排序Tab.4 Ordering of the models 按Borda数的大小进行排序:B(BP)>B(RBF)>B(RF)>B(SVR),则综合预测性能最优的是BP神经网络,其次是RBF神经网络,再次是随机森林RF,最次的是支持向量回归SVR。 (1)基于机器学习模型计算的含非淹没刚性植被水流流速的垂向分布与实际测量值拟合良好,能够较好地反映含植被水流层间的流速变化。 (2)根据流量、水深和纵向距离等变量便可结合机器学习方法对具体数据自适应建模,必要输入参数较少,能对离散流速值间的空白进行预测和填补。 (3)BP神经网络的综合预测性能最优,而其余模型误差较大。保证训练数据的质量和合理选取机器学习的模型能够有效提高预测值的可信度。同时在工程计算中可考虑综合使用多种模型,进一步提高预测结果的使用价值。 □2 试验装置与测量设备
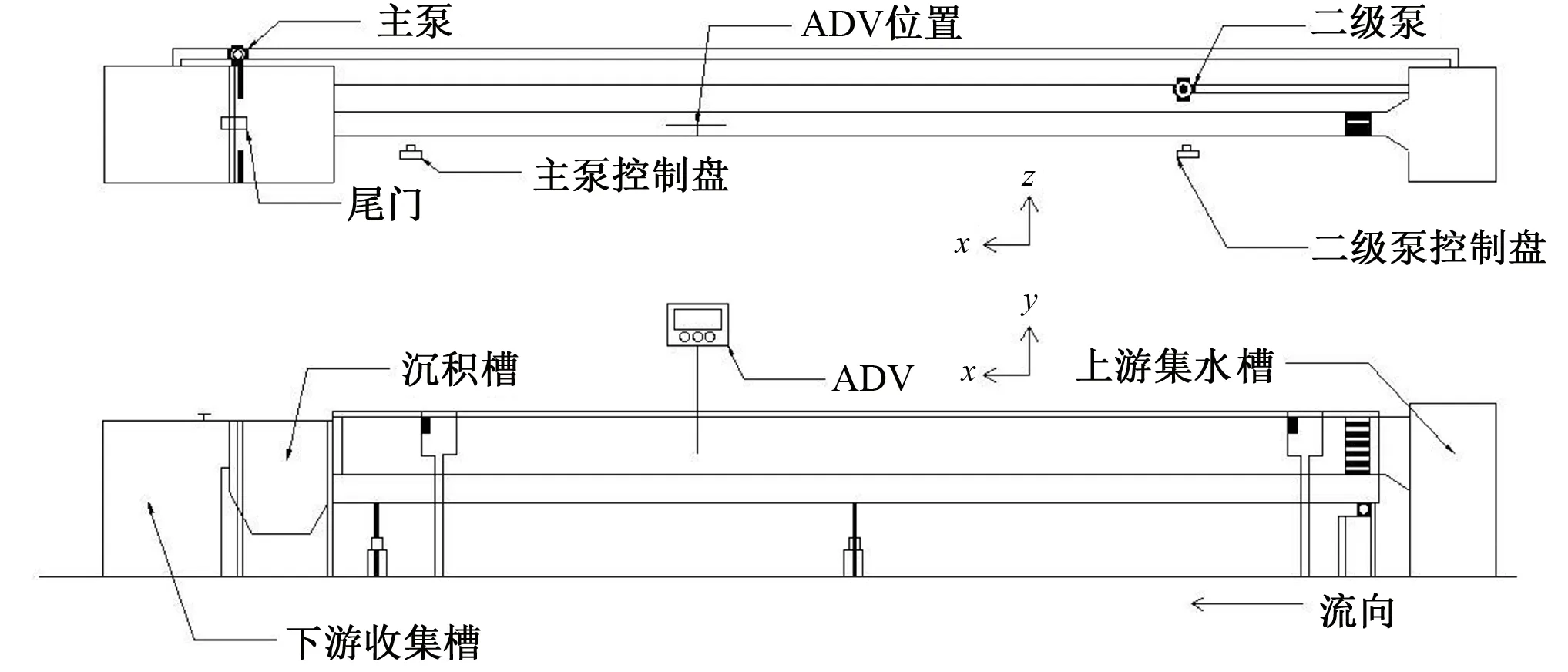

Tab.1 Summary of test conditions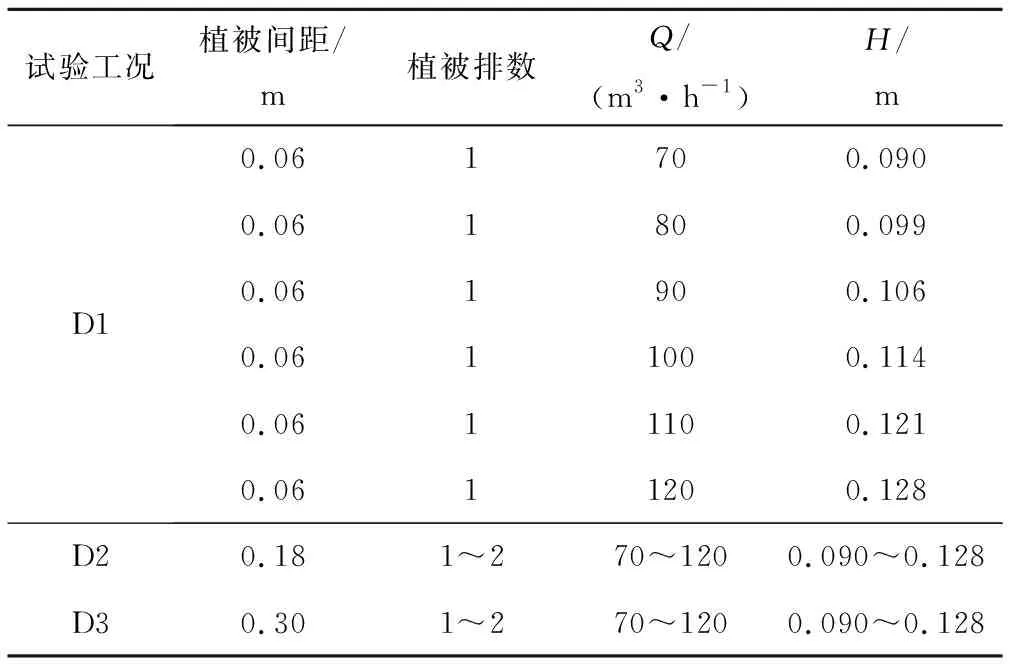
3 数据的分析及处理
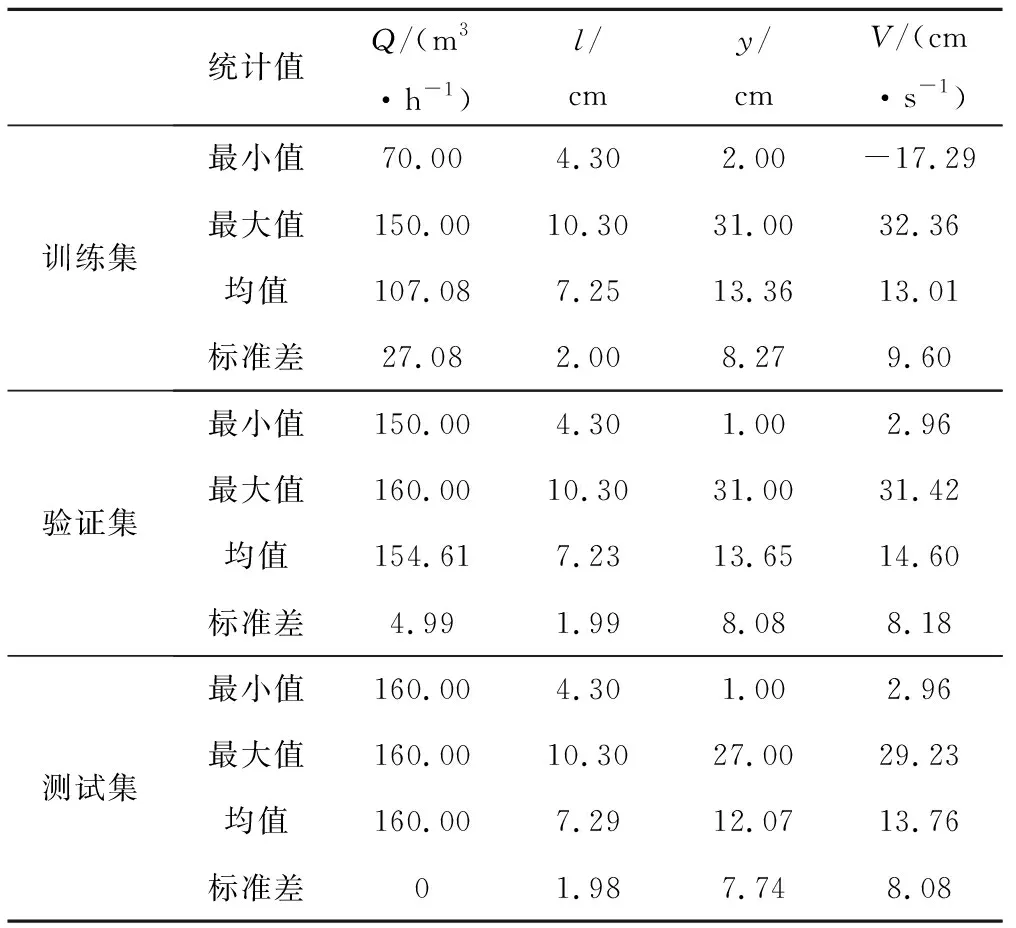
4 模型的训练情况
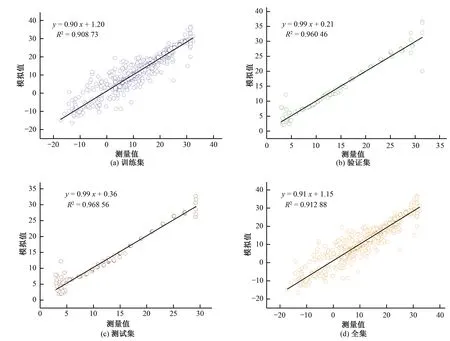
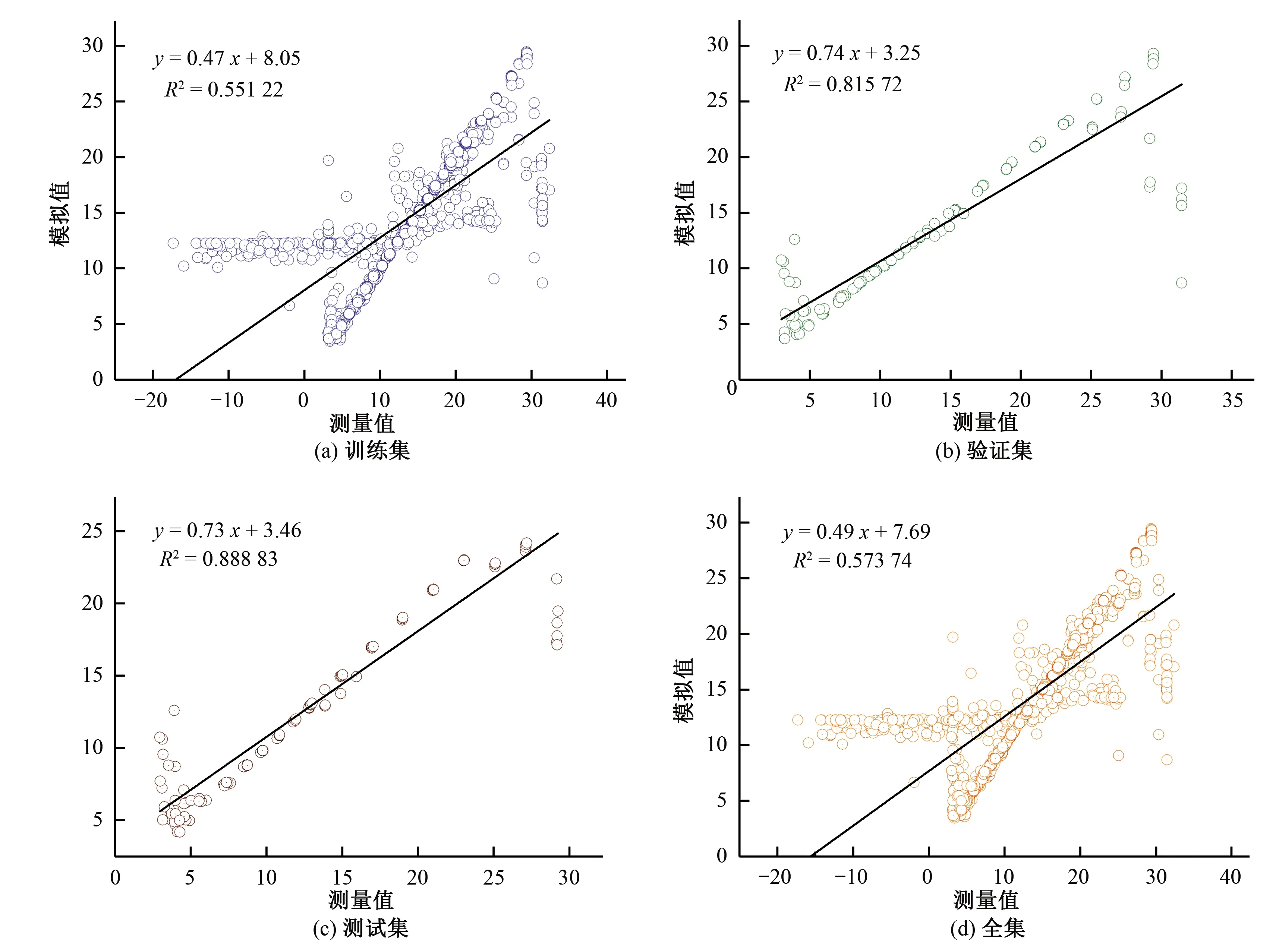
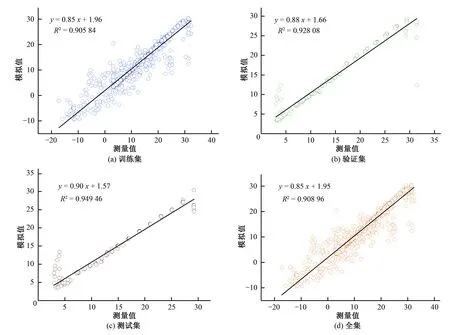
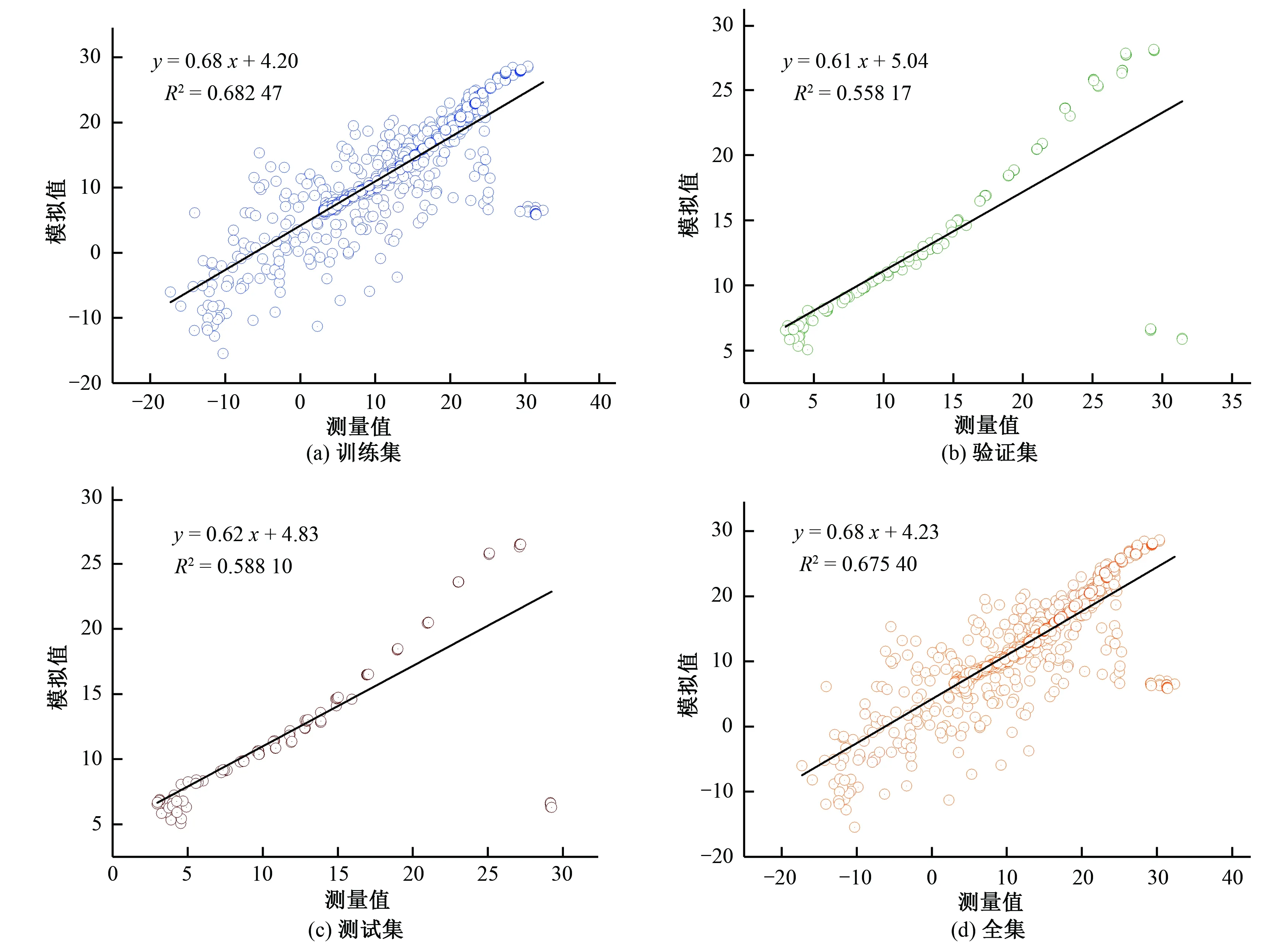
5 模型结果及验证
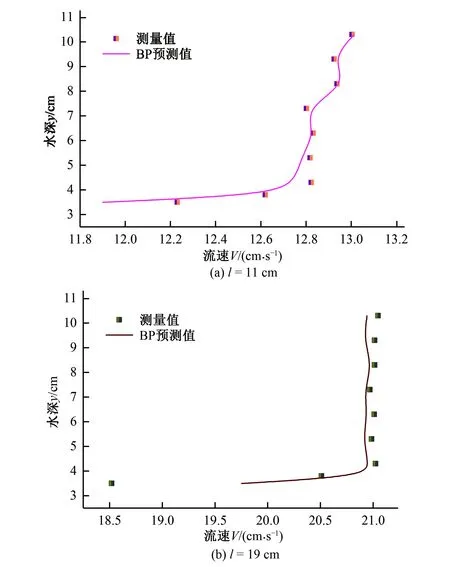
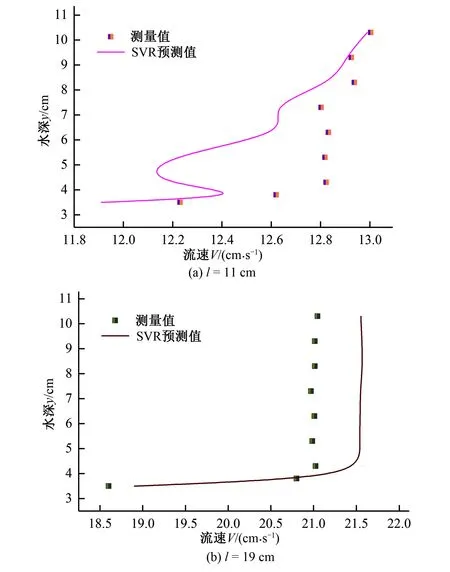
6 模型的综合评价
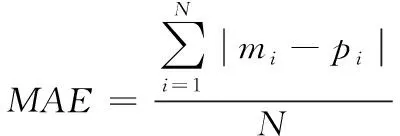
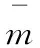

7 结 论

