调压室参数对水力干扰下机组调节品质的影响分析

曹林宁，吴道科，邓正海

(1.河海大学 能源与电气学院，南京 210098；2.重庆蟠龙抽水蓄能电站有限公司，重庆 401422)

0 引 言

随着我国清洁能源的大力推广与发展，水电站作为一种绿色可持续发展的发电源其规模正在逐年扩大。对于目前大部分的长引水式电站或抽水蓄能电站，为了缩小投资成本往往会选择一管多机的布置形式[1]，多台机组通过岔管连接，共用引水主管和调压室。对于一管多机布置形式的电站，由于机组间的水力联系密切往往会导致当某些机组突然丢弃满负荷或大幅度的增加负荷时其他正常运行机组受到影响，机组出力产生摆动，此时机组即处于水力干扰过渡过程之中[2, 3]。水力干扰不同于大波动和小波动过渡过程，它是由机组间的相互影响产生的，轻则影响正常运行机组的发电品质，重则危及电站的安全稳定运行[4]，所以对于一管多机的电站水力干扰过渡过程展开深入研究是十分重要的。陈乃祥、梅祖彦等很早就提出了抽蓄电站水力干扰下的过渡过程及稳定性问题的研究[5]；孙美凤则针对引水式电站并列运行机组建立了MATLAB仿真模型并对水力干扰现象进行了研究[6, 7]；张显羽则研究了机组转动惯量对水力干扰下机组调节品质的影响[8]；赖旭通过引入三阶发电机模型、励磁模型和负载模型建立完整的水机电联合仿真模型，研究了调速器参数对电站水力干扰过渡过程的影响[9]；周攀、邓磊等则对不同调速器调节模式下的机组水力干扰影响试验进行了分析[10]；余平则以实际电站为例，详细介绍了“一洞双机”电站机组开机、负荷调整和安控切机策略等研究方法，为类似电站提供参考[11]。对于一管多机的电站，调压室的作用是十分重要的，前人往往针对大波动过渡过程研究调压室参数的影响[12-14]，而对于水力干扰现象则鲜有涉及。本文以某双机共用引水调压室的抽水蓄能电站为例，选择两个典型的水力干扰工况以及不同的调节模式，通过建立电站仿真模型计算分析了调压室面积、阻抗孔面积以及阻抗孔流量系数对于水力干扰工况下正常运行机组调节品质的影响。

1 水力干扰过渡过程数学模型

1.1 有压管道弹性水击模型

有压管道的非恒定流一维弹性水击偏微分方程[15]为：

(1)

式中：H(x,t)为测压管水头；V(x,t)为水流速度；a是水击波速；f为管道沿程损失系数；θ为管道各个截面形心的连线和水平面的夹角；x和t分别为管道长度和时间。

针对上式通过特征线法求解后可以得到一组特征相容方程：

C+:HPi=CP-BPQPi

C-:HPi=CM+BMQPi

(2)

式中：CP、BP、CM、BM前一时刻的已知值。

1.2 阻抗式调压室数学模型

如图1所示，引水调压室通过阻抗孔和引水主管连接，则其平衡方程为：

(3)

式中：Hi、QPi、Si分别对应图中的测压管水头，流量以及管道截面积；HS表示调压室水位；QS、RS分别为流入调压室的流量(QS为负数则表示流出调压室流量)和阻抗孔的流量损失系数，其中RS的计算公式为：

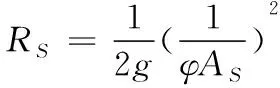
(4)

式中：AS为阻抗孔面积；参数中含有下标0的即为前一时刻的已知值；φ为阻抗孔流量系数，一般取0.6～0.8。

图1 阻抗式调压室结构简图Fig.1 structural diagram of impedance surge tank

对P节点构造特征相容方程得：

C+:H1=CP1-BP1QP1

C-:H2=CM2+BM2QP2

(5)

根据水流连续性可得：

QP1=QS+QP2

(6)

又调压室水位和流量之间的关系为：

(7)

联立式可求解各个未知量。

1.3 岔管边界条件

如图2所示引水岔管结构图，根据水流连续方程有：

QP1=QP2+QP3

(8)

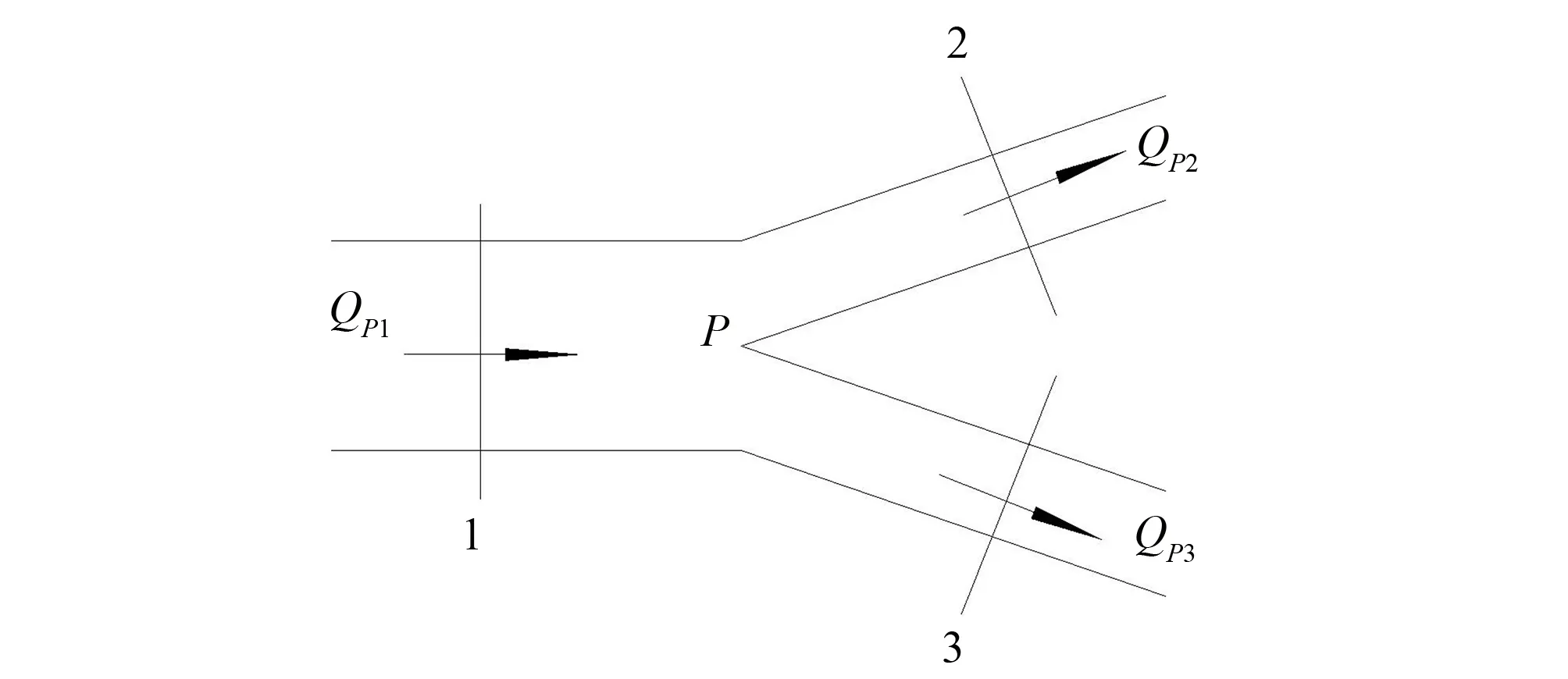
图2 岔管结构图Fig.2 Structure of bifurcated pipe

由能量方程有：

HP1=HP2=HP3=HP

(9)

建立特征相容方程得：

C1+:HP1=CP1-BP1QP1

C2-:HP2=CM2+BM2QP2

C3-:HP3=CM3+BM3QP3

(10)

1.4 水轮机特性模型

基于水泵水轮机四象限特性曲线的水轮机非线性模型全面考虑到影响水轮机流量及力矩因素，故能更加真实地反映出水轮机的动态特性。因此，本文选择其特性方程为：

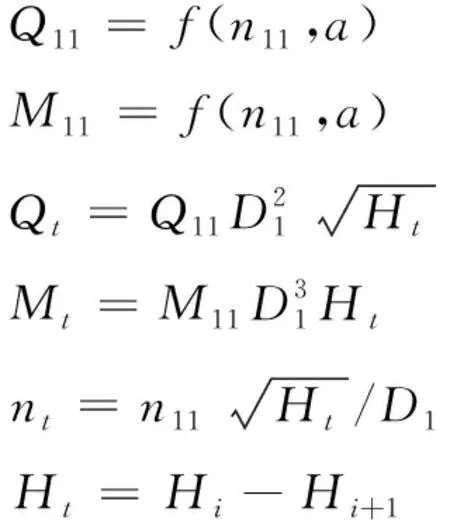
(11)

式中：Q11、M11、n11相应为水轮机单位流量、单位力矩和单位转速；Qt、Mt、nt相应为水轮机流量、力矩和转速；Ht、Hi、Hi+1相应为水轮机水头、机组前节点水压力和机组后节点水压力；a为导叶开度。

由于水泵水轮机特性曲线中存在“S”区域，全特性在以单位流量Q11(单位力矩M11)和单位转速n11为纵、横坐标的平面内呈现多值性，在过渡过程计算中，一般需将它们转换到极坐标中，可以得到以x为横坐标的WH(x)曲线和WM(x)曲线，变化公式如下：

(12)

式中：n和nb为转速和转速基值；Q和Qb为流量和流量基值；H和Hb为水头(扬程)和水头(扬程)基值；M和Mb为力矩和力矩基值；n11b为单位转速基值；Q11b为单位流量基值；M11b为单位力矩基值。

又根据水轮机水头平衡方程有：

(13)

式中：h，q为相对水头和相对流量；Hr、Qr为额定水头和额定流量。

发电机及负载部分采用一阶模型，其力矩平衡方程为：

(14)

式中：J为水轮机和发电机部分总转动惯量；ω转子(机组)旋转角速度；Mt、Mg分别为水轮机动力矩和发电机及负载阻力矩。

1.5 调速器模型

本文选择PID调节器+电液随动系统的调速器模型，当机组处于频率调节模式时，调速器采用并联PID型调速器，相应调节模型如图3所示(由于机组并大网运行时频率与电网频率保持一致，故此时调速器不参与动作)；当机组处于功率调节模式时调速器采用PI型控制形式，微分环节切除，相应调节模型如图4所示。图中KP，KI，KD分别为比例增益、积分增益和微分增益；Tn为微分时间常数；Ty为接力器时间常数；bp为永态转差系数；s为拉普拉斯算子。

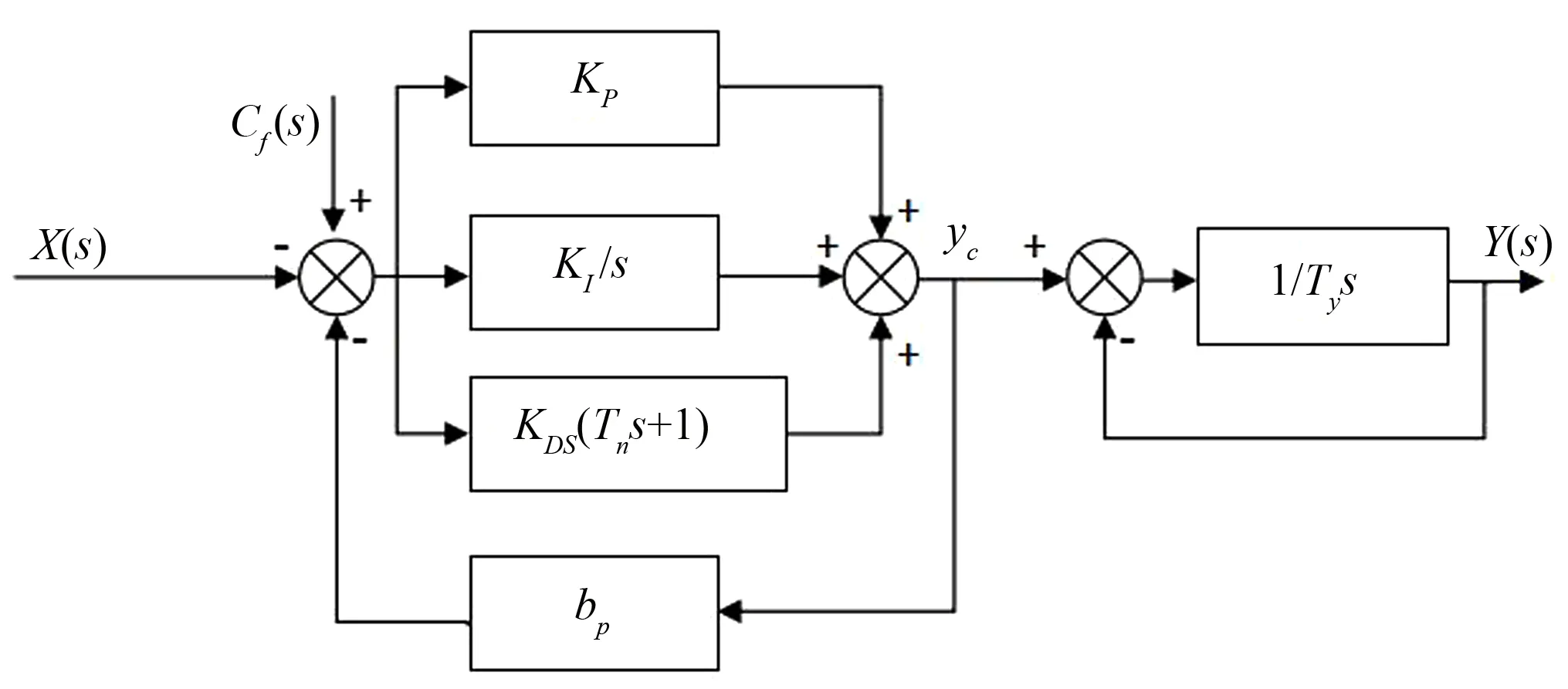
图3 频率调节模式下调速器模型Fig.3 Model of speed regulator in frequency regulation mode

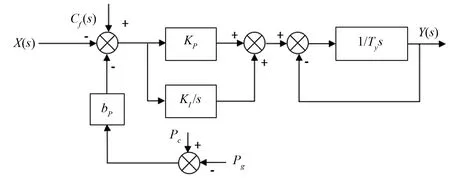
图4 功率调节模式下调速器模型Fig.4 Model of speed regulator in power regulation mode

2 算例分析

2.1 电站基本参数

如图5所示，我国某抽水蓄能电站呈一管双机布置形式，两台机组共用引水主管和引水调压室，在引水岔点之后两条引水支管分别连接着两台机组，随后机组通过各自尾水隧洞分别与下游水库相连。此时，若其中一台机组突然丢弃较大负荷或者启动增满负荷，流量的变化必定会通过引水主管和调压室影响到另一台正常运行的机组，导致其出现出力、转速、蜗壳压力以及尾水管压力波动的现象，严重时甚至会危及机组安全稳定运行。

图5 一管双机抽蓄电站布置简图Fig.5 layout of one pipe double unit pumped storage power station

电站采用两台300 MW混流可逆式水泵水轮电动发电机组，具体参数见表1。

表1 机组特性参数Tab.1 Unit characteristic parameters

2.2 仿真计算分析

为了研究调压室参数对水力干扰过渡过程中正常运行机组调节品质的影响，本文根据调压室大井面积、阻抗孔直径以及阻抗孔流量系数的不同选择若干组合情况见表2。

表2 不同调压室参数组合Tab.2 Different parameter combinations of surge tank

注：各组合中引水主管直径、支管直径和调压室位置等均相同。

选择两种典型水力干扰工况如下：

A：上游水位984.00 m，下游水位544.00 m，额定水头下两台机组带额定负荷正常并网运行时，2号机突甩100%负荷。

B：上游水位984.00 m，下游水位544.00 m，额定水头下1号机带额定负荷正常并网运行时，2号机启动增至满负荷。

对于水力干扰过渡过程中正常运行机组，其调节品质的优劣主要体现在机组最大出力摆动、超调量、调节时间和振荡次数等指标。为了研究调压室参数对于水力干扰下正常运行机组调节品质的影响，本文针对不同的调压室参数组合，选择两种典型的水力干扰工况，并分别对频率调节和功率调节模式下水力干扰过渡过程进行数值模拟计算，分析不同工况下机组调节品质优劣。为了消除其他因素的影响，所有计算工况中调速器参数的取值均保持一致，其中KP，KI，KD的取值分别为2,0.3和0.5；微分时间常数Tn取值为0.1；永态转差系数bp取值为0.04。

组合编号1、2、3、4考虑不同阻抗孔面积对水力干扰过渡过程下1号机调节品质的影响，其结果见表3。

1号机出力和调压室涌浪随时间变化曲线如图6～9所示。

从表3可以看出，对于水力干扰工况A，不论是采取频率调节模式或是功率调节模式，1号机的受扰情况较大其出力摆动均在22%左右，且在频率调节模式下，1号机最大出力摆动较功率调节模式下略大。随着阻抗孔面积的增大，1号机最大出力摆动逐渐减小，并且减小的速率不断下降，d=2.2 m和d=4.0 m时1#机最大出力摆动相差2.5%左右；而对于水力干扰工况B，1号机的最大出力摆动较小均在5%左右，同样在频率调节模式下，1号机最大出力摆动较功率调节模式下略大，且随着阻抗孔面积的增大，机组最大出力摆动略有减小。从图6～9可以看出，对于水力干扰工况A和B，随着阻抗孔面积的增大，1号机出力随时间变化曲线的超调量呈现增大趋势，并且机组出力振荡次数和调节时间都不断增加。2号机负荷突变引起的流量变化在管道内产生水击压力传至调压室时大部分被反射，反射波与入射波叠加使得管道内水击压力减小从而导致运行机组出力的变化幅值降低，较大的阻抗孔面积增强了反射波作用使得1号机最大出力摆动减小。但同时阻抗孔面积增加使得调压室涌浪变化幅值增大，水位波动衰减慢，调压室水位持续变化通过管道流量影响运行机组出力尾波品质，从而导致1号机出力恢复稳定状态的时间增加。以上分析说明阻抗孔面积对于水力干扰过渡过程中正常运行机组的调节品质有较大影响，随着阻抗孔面积的增加，虽然正常运行机组的最大出力摆动有所下降，但是其恢复稳定状态的时间变长。针对这种情况，可以选择适中阻抗孔尺寸d=2.7 m使得正常运行机组最大出力摆动较小的同时又能在较短时间内恢复到稳定状态。

表3 不同阻抗孔尺寸下水力干扰过渡过程计算结果Tab.3 Calculation results of hydraulic interference transition process under different impedance hole sizes

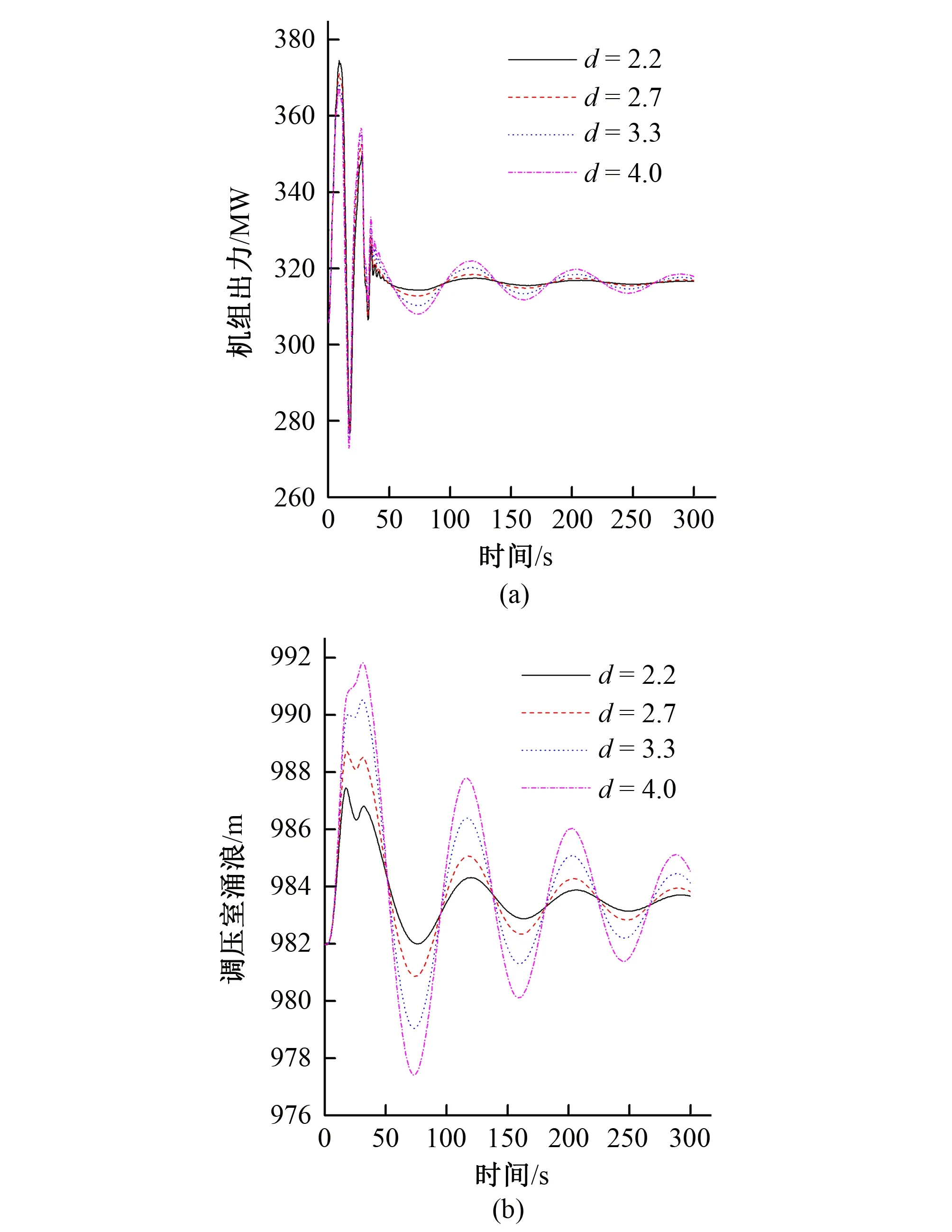
图6 频率调节时1号机在工况A下出力和调压室涌浪随时间变化曲线Fig.6 Time varying curve of output and surge in surge tank of unit 1 under condition A during frequency regulation

图7 功率调节时1号机在工况A下出力和调压室涌浪随时间变化曲线Fig.7 Time varying curve of output and surge in surge tank of 1 unit under condition A during power regulation

图8 频率调节时1号机在工况B下出力和调压室涌浪随时间变化曲线Fig.8 Time varying curve of output and surge in surge tank of unit 1 under condition B during frequency regulation

图9 功率调节时1号机在工况B下出力和调压室涌浪随时间变化曲线Fig.9 Time varying curve of output and surge in surge tank of 1 unit under condition B during power regulation

组合编号2,6,7考虑的是调压室大井面积对于水力干扰过渡过程中1号机调节品质的影响，其结果见表4。

1号机出力和调压室涌浪随时间变化曲线如图10～13所示。

从表4可以看出，1号机在水力干扰工况A下的最大出力摆动较大，均在21%左右。并且随着调压室大井面积的增大，两种工况下正常运行机组最大出力摆动变化较小。观察图10～13发现，随着大井面积的增加，机组出力超调量有小幅度降低，振荡次数和调节时间也都随之减小。分析原因可从调压室涌浪随时间变化曲线发现：随着大井面积减小，调压室涌浪变化幅值增加，水位波动衰减慢，恢复稳定状态时间延长，调压室水位的持续波动通过管道流量影响1号机出力的尾波品质，从而导致1号机组出力出现持续的震荡，恢复稳定状态的时间延长。以上分析说明调压室大井面积对于水力干扰下正常运行机组出力调节时间和振荡次数有一定改善作用，因此可以适当增加调压室大井面积使得机组在水力干扰工况下能在较短时间内恢复稳定运行状态。

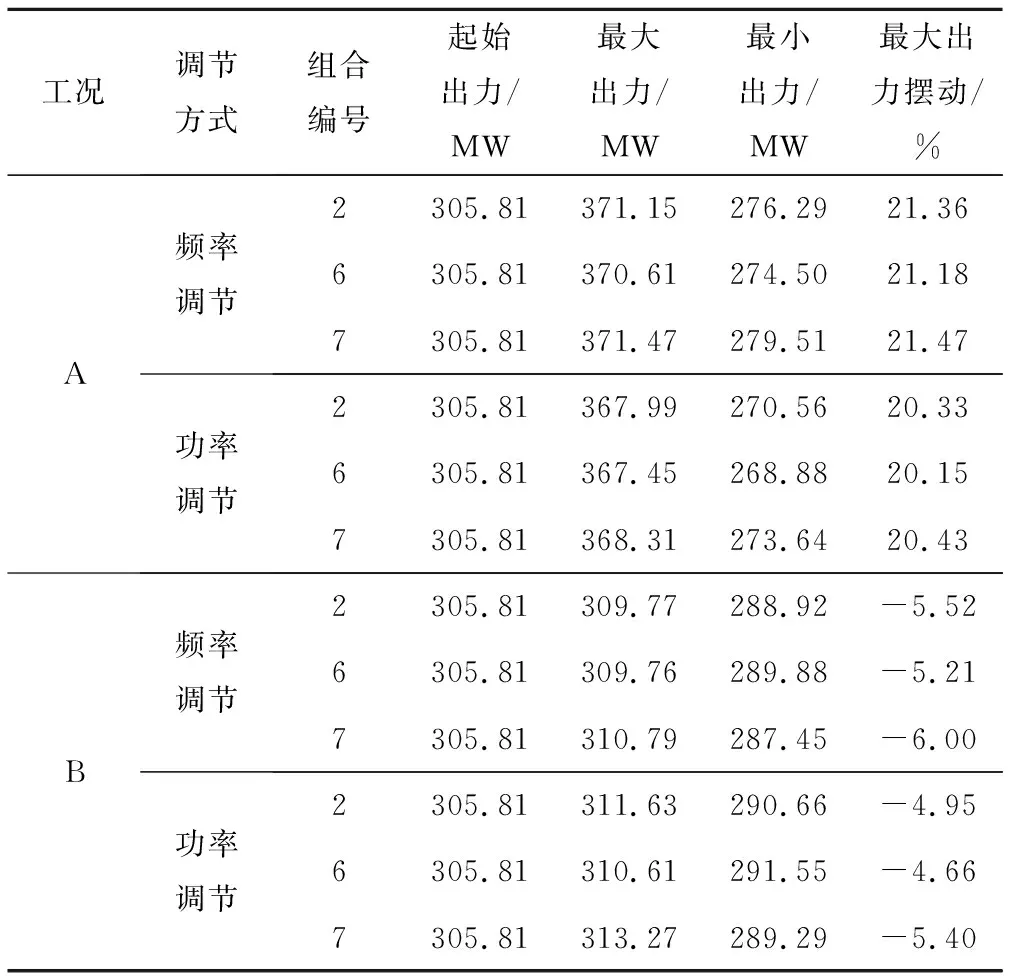
表4 不同调压室大井面积下水力干扰过渡过程计算结果Tab.4 Calculation results of hydraulic interference transition process under different surge tank and large well area

组合编号2,5考察的是阻抗孔流量系数对于水力干扰过渡过程中正常运行机组的影响，此时机组出力和调压室涌浪变化曲线如图14～17所示。

由图14～17可以看出，在水力干扰过渡过程中当阻抗孔流量系数变化时，正常运行机组最大出力摆动有较小差异，超调量、振荡次数、调节时间等基本没有变化，调压室涌浪变化趋势基本一致，仅在第一个波峰(波谷)处的幅值略有差距。说明阻抗孔流量系数对于水力干扰工况下正常运行机组调节品质影响较小。

3 结 论

在一管双机布置形式的电站中，由于两台机组共用引水主管和引水调压室，水力联系密切，当其中一台机组出现负荷的大幅度变化时会使得另一台正常运行机组受到影响。为了研究调压室参数对水力干扰过渡过程中正常运行机组调节品质的影响，本文基于特征线法建立了某一管双机抽水蓄能电站的仿真模型，并选择两种调节模式和不同调压室参数组合对该电站两个典型的水力干扰工况进行数值计算分析，结果表明：①相对于频率调节模式，功率调节模式下机组在水力干扰过渡过程中的最大出力摆动较小；②阻抗孔面积对机组在水力干扰过渡过程中调节品质影响较大，当阻抗孔面积增大时，机组最大出力摆动逐渐减小，但同时机组出力超调量、振荡次数和调节时间均有所增大。因此，在满足电站调节保证计算要求的前提下可以选择适当阻抗孔尺寸d=2.7 m使得正常运行机组最大出力摆动较小的同时又能在较短时间内恢复稳定状态；③调压室大井面积对于机组在水力干扰过渡过程中调节品质有一定影响，随着大井面积增加受扰机组出力振荡次数和调节时间会有所下降。因此可以适当选择较大调压室大井面积来提高机组调节品质。④阻抗孔流量系数对机组在水力干扰过渡过程下的调节品质影响较小。

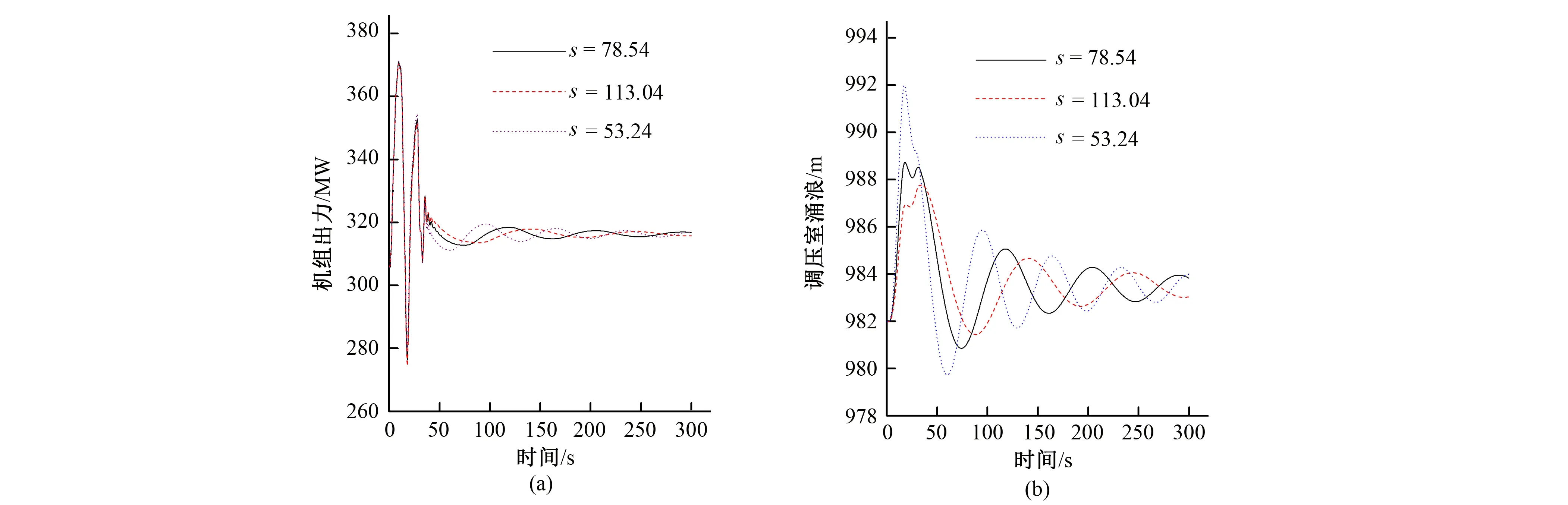
图10 频率调节时1号机在工况A下出力和调压室涌浪随时间变化曲线Fig.10 Time varying curve of output and surge in surge tank of unit 1 under condition A during frequency regulation

图11 功率调节时1号机在工况A下出力和调压室涌浪随时间变化曲线Fig.11 Time varying curve of output and surge in surge tank of 1 unit under condition A during power regulation

图12 频率调节时1号机在工况B下出力和调压室涌浪随时间变化曲线Fig.12. time varying curve of output and surge in surge tank of unit 1 under condition B during frequency regulation

图13 功率调节时1号机在工况B下出力和调压室涌浪随时间变化曲线Fig.13 Time varying curve of output and surge in surge tank of 1 unit under condition B during power regulation

图14 频率调节时正常运行机组在工况A下出力和调压室涌浪随时间变化曲线Fig.14 Time varying curve of output and surge in surge tank of unit 1 under condition A during frequency regulation

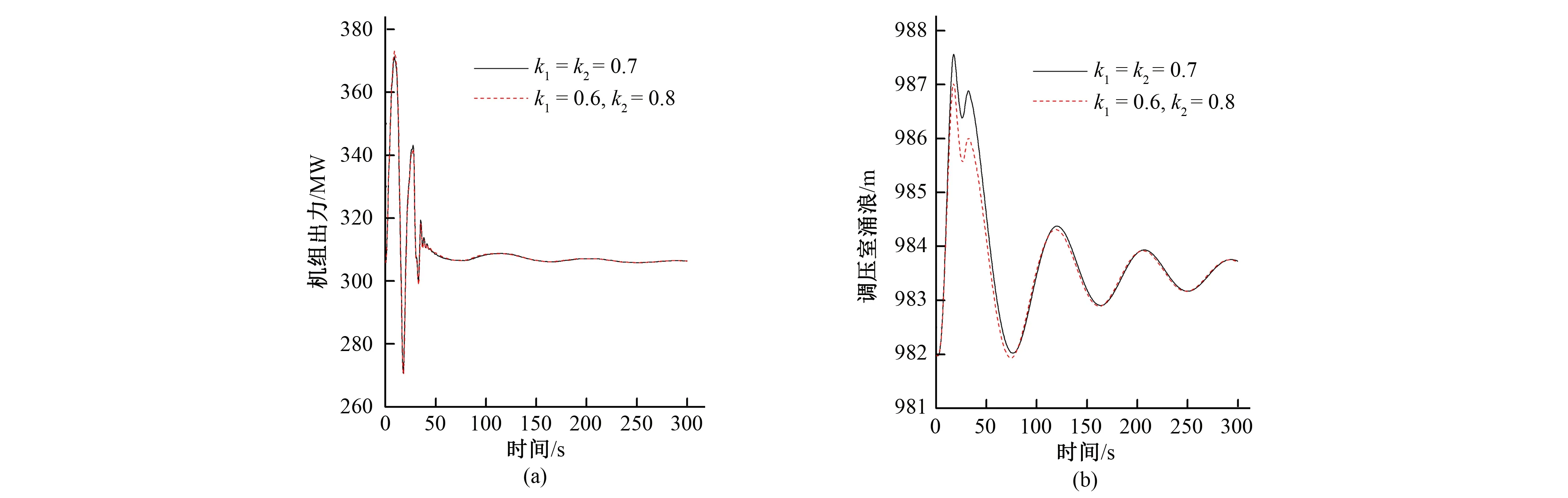
图15 功率调节时正常运行机组在工况A下出力和调压室涌浪随时间变化曲线Fig.15 Time varying curve of output and surge in surge tank of 1 unit under condition A during power regulation

图16 频率调节时正常运行机组在工况B下出力和调压室涌浪随时间变化曲线Fig.16 Time varying curve of output and surge in surge tank of unit 1 under condition B during frequency regulation

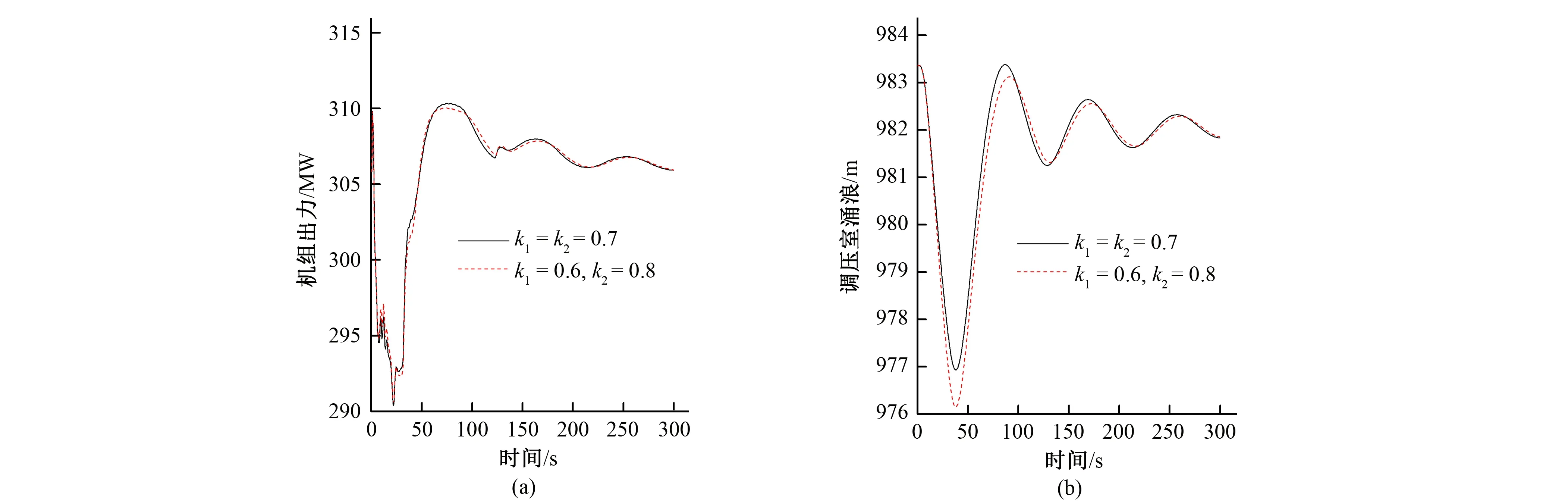
图17 功率调节时正常运行机组在工况B下出力和调压室涌浪随时间变化曲线Fig.17 Time varying curve of output and surge in surge tank of 1 unit under condition B during power regulation

□