基于改进分析方法的滑坡失稳概率研究
蒲书豪,任光明,王 滨,陈 谦,陈中国,吕俊杰
(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059;2.国家电网四川省电力公司 成都 610041; 3.国家电网四川省电力公司 经济技术研究院 成都 610041)
目前大多数的滑坡相关工程,在判断坡体稳定状态时,依靠的仅仅是对滑坡典型剖面通过岩土体物理力学参数的统计平均值进行稳定性计算,得到的结果往往只能在一定程度上反映滑坡体的稳定性。而实际上,即使是滑坡体同一土层,其不同位置的岩土体参数也不完全一样,其参数是一个具有不确定性、变异性及离散性的动态范围[1]。因此计算得到的安全系数也应该是一个呈动态变化的范围,那么单纯依据计算得到的安全系数定值来判断滑坡的稳定性是不合理的。
早在20世纪50年代,A.M.Freudenthal[2]就提出将概率分析方法引入工程结构可靠性分析中;通过不断地学习探索,到了20世纪80年代,祝玉学[3]将这种分析方法应用到土坡稳定性分析中并出版了中国第一部相关著作《边坡可靠性分析》,从此,概率分析逐渐成为一种热门的稳定性评价手段;徐卫亚等[4]通过概率分析法对大岩淌滑坡进行了1 000次稳定性计算,得到其失稳概率及稳定性等级;李强等[5]通过选择重度、黏聚力及内摩擦角作为随机变量进行了50 000次稳定性计算得到滑坡的可靠度。然而随着概率分析在滑坡工程上的不断应用,其不足之处也逐渐显露出来,要想得到滑坡体的失稳概率,应在合理恰当地考虑参数动态变化的基础上进行分析;如果未考虑重要参数的不确定性,那么得到的分析结果将会失真;但若考虑全部参数的不确定性,不仅参数获取困难,且计算工作也繁琐[6]。
在此背景下,本文提出将敏感性分析与概率分析法相结合的分析手段,以敏感性分析结果的针对性来弥补概率分析法参数选取上的不足,以期得到更具有针对性、高效的计算结果,更好地为滑坡防治工程提供参考。
1 滑坡失稳概率计算方法
为使分析更系统高效,首先通过基于灰色关联分析法的敏感性分析得到影响坡体稳定性的主导因素,再在分别考虑这些主导因素的变异性及离散性的基础上进行基于蒙特卡洛模拟法的滑坡失稳概率分析,最后根据主导因素与稳定性的关联程度所占权重综合进行计算滑坡失稳概率。由于只对主导因素的参数要求较高,所以不仅可以有效减少勘察及计算的工作量,得到的结果对于后续的防治工程也更具针对性。
1.1 灰色关联分析
灰色关联分析引用了“数学中曲线相似程度判断关系”的思维,选取最能反映系统行为特征的数据序列为母序列Y,并提取相关因素数据序列为子序列X,通过母序列与子序列曲线的相似度来判断两者的关联程度[7-8]。子序列、母序列矩阵表达式如下
因子序列中各因素有不同的量纲,所以对子序列X用xi(j)/xi(1)依次代替各数据进行初值法去量纲处理。
然后计算子序列X与母序列Y在k点的关联系数
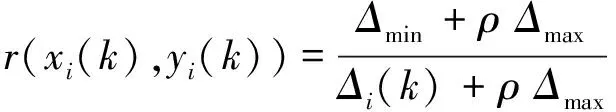
(1)
式中:Δi(k)=|xi(k)-yi(k)|;ρ为提高关联系数间差异性的分辨系数,通常取0.5。
最后将关联系数取平均值作为关联度,即

(2)
本文所得各因素的关联度即代表了稳定性影响因素与稳定性的关联程度。
1.2 蒙特卡洛模拟法
蒙特卡洛模拟法实质为一抽取随机数的模拟方法,通过对关键变量进行符合其概率分布特点的随机数抽取,再将其代入状态函数进行计算,通过状态函数结果的分布来得到所需要的几率结果。且由伯努利大数定律可知,在随机事件的大量重复出现中,往往呈现几乎必然的规律,当模拟次数足够大时,几率可近似等于其概率[9]。如模拟次数为N次,其中有M次出现安全系数f<1,则滑坡的失稳概率Pf=M/N。实际上,当模拟次数足够大时,由大量的安全系数值统计样本能较精准地拟合出安全系数的概率分布函数,其均值和标准差分别为[10-12]
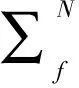
(3)
(4)
其中Ki为状态函数结果值,本文为安全系数。
然后由中心极限定量可知,在N≥50的条件下,失稳概率的积分表达式为
(5)
2 实例分析
2.1 滑坡简介
本文以丹巴500 kV变电站进场道路1#滑坡为例。该滑坡体多年来均处于稳定状态,但在邻近变电站进场道路修建过程中的无支护开挖作用下,坡体的稳定状态发生了改变,在次年雨季由于强降雨的影响,导致部分坡体失稳发生滑动。若再次滑动,将会严重影响道路的修建以及下部居民区的安全。故本文通过对其失稳概率的计算,为其防治工程提供参考。
滑坡呈圈椅状,微地貌呈坡形地貌,坡度较陡,中上部坡度在24°~30°,下部坡度在40°左右,主滑方向32°,前缘的海拔高度约为1 940 m,后缘的海拔高度约为2 080 m,相对高差140 m。前缘宽约54 m,纵长约262 m,平均厚度约为12 m,滑坡体的体积约为0.169×106m3,为中型堆积体滑坡。
根据野外调查及勘察资料,滑坡的滑体部分为第四系覆盖层,主要为含角砾粉质黏土,土体较干燥,结构松散;滑带部分为基覆界面的第四系堆积层的软弱带土体,土体稍湿,为可塑状态;滑床部分为片岩,深度不同则风化程度不同。典型剖面计算模型见图1。
2.2 滑坡体稳定性影响的主导因素
该滑坡体在雨季强降雨的影响下发生失稳滑动,其影响坡体稳定性主要体现在雨水入渗导致土体重度增加以及软化基覆界面土体,使其抗剪强度降低。因此,选择土体的重度、黏聚力、内摩 擦角、土体渗透系数及降雨量5个因素作为稳定性敏感性分析的主要因素。
根据现场调查、室内试验以及当地气象资料,确定敏感性分析参数的基准值如表1,通过控制其中4个因素不变,以对称加减的方式改变另一个因素的值的方法来获得子序列X的元素,再通过使用Geo-studio软件中的Slope/W模块进行稳定性计算,计算方法选用满足力和力矩平衡的Morgenstern-Price法,得到安全系数作为母序列Y中的元素,得到的序列如下:
然后对子序列X进行初值法去量纲处理,再由式(1)得到关联系数序列r(k)

表1 敏感性分析参数基准值Table 1 Baseline values of sensitivity analysis parameters
最后根据式(2)计算得到各因素与安全系数的关联度序列r
r=(0.635 0.651 0.675 0.591 0.601)T
根据计算所得各因素的关联度序列,得到各因素的敏感性顺序为:内摩擦角>黏聚力>重度>降雨量>渗透系数。表明影响坡体稳定性的因素中,仍是土体本身的强度参数最为敏感,因此选取黏聚力和内摩擦角作为主导因素,根据灰色关联度求解指标权重的改进方法[13],由关联度计算结果得到黏聚力及内摩擦角所占权重分别为0.491、0.509,在考虑其参数的变异性及离散性的情况下分别进行滑坡失稳概率分析,再依据所占权重综合计算滑坡的失稳概率。
2.3 滑坡失稳概率
前面由灰色关联度敏感性分析得到了影响滑坡稳定性的主导因素为黏聚力和内摩擦角,选其为失稳概率分析关键变量。因为常见土性指标一般服从正态分布,且通常抽样次数在5 000~10 000次即可满足计算精度[14-17],所以通过蒙特卡洛模拟法分别抽取黏聚力值和内摩擦角值的随机数10 000次,其余参数采用基准值,通过稳定性计算状态函数计算得到结果。计算继续使用Geo-Studio软件中的Slope/W模块,计算方法为Morgenstern-Price法,通过软件中内置的蒙特卡洛概率计算进行随机数的抽取,参数设置见表2。根据《滑坡防治工程设计与施工技术规范》(DZ/T 0219-2006),需计算3种工况:天然工况、暴雨工况和地震工况。滑坡区地震加速度值参考国家标准《中国地震动参数区划图》(GB 18306-2015)取为1.47 m/s2(重力加速度取9.8 m/s2)。
根据计算结果,得到不同主导因素各工况安全系数分布概率(图2、图3、图4),该滑坡体在3种工况下的平均安全系数及失稳概率统计结果如表3。

表2 土体参数设置Table 2 Soil parameter setting
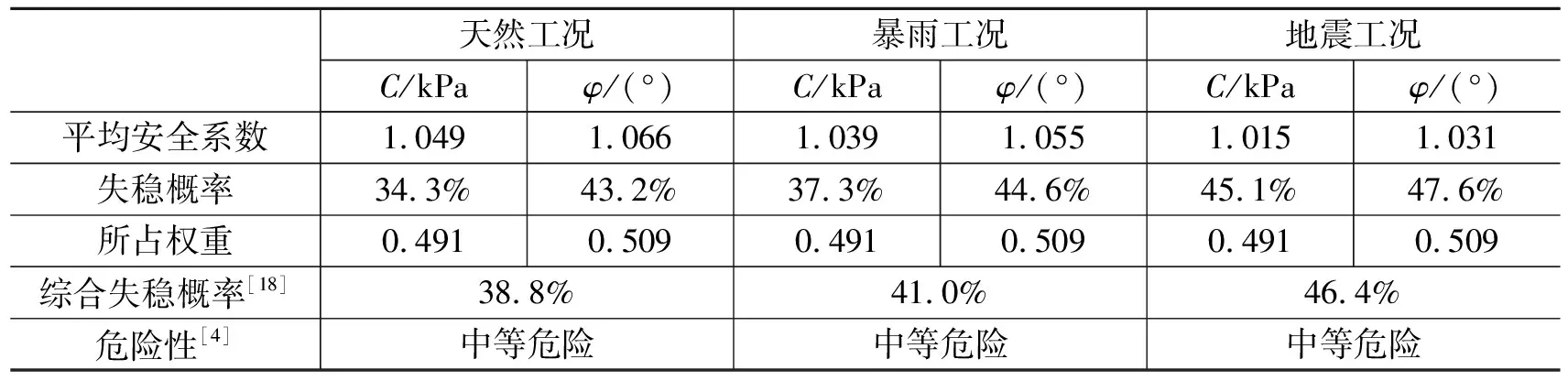
表3 滑坡失稳概率计算结果统计Table 3 Statistics of calculation of probability of landslide instability
3 结 论
a.通过基于灰色关联分析法的敏感性分析,得到该滑坡体稳定性影响因素的敏感性顺序为:内摩擦角>黏聚力>重度>降雨量>渗透系数,其主导因素为内摩擦角和黏聚力,两者所占权重分别为0.509、0.491。
b.在已知影响滑坡稳定性主导因素及其所占权重的基础上,通过基于蒙特卡洛模拟法的滑坡失稳概率分析,得到该滑坡在天然工况下再次失稳滑动的概率为38.8%,在暴雨工况下再次失稳滑动的概率为41.0%,在地震工况下再次失稳滑动的概率为46.4%。
c.通过该实例分析,得出相比传统多因素概率分析方法的工作量,将灰色关联分析法与蒙特卡洛模拟法相结合来分析滑坡失稳概率的方法是高效可行的。该方法不仅有效减少了工作量,还在敏感性分析的条件下保证了其结果的针对性及准确性。

