警觉与疾病的传播次序性对动力学的影响

阚佳倩，马 闯，张海峰

(1. 安徽科技学院信息与网络工程学院 安徽 蚌埠 233030；2. 安徽大学互联网学院 合肥 230601；3. 安徽大学数学科学学院 合肥 230601)

近年来，随着对复杂网络科学认识的深入，科学家们发现很多的真实系统都可以用多层网络结构进行更精确的描述。例如，人际关系网中的线下朋友关系以及线上朋友关系等；不同运输工具(航空网、铁路网和公路网)构成的交通网络等。因此关于多层网络的结构及动力学的研究已经成为网络科学领域的一个研究热点和重点[1-11]。

传染性疾病的爆发会引发相关的信息通过人群内部、新闻媒介以及在线社交网络等多种渠道传播，而人们获得该信息后会警觉且采取一定的预防措施自我保护，从而对疾病传播产生深远的影响。已有学者在研究传染病动力学的时候开始从不同角度考虑信息因素的影响，如：个体根据对疾病信息的了解程度来调整与外界的接触情况[12]，个体行为方式的改变[13]，人群内部、新闻媒介以及在线社交网络传播信息对疾病传播的影响[14]；文献[15]基于传 统 的“ S(susceptible)-I(infected)-S(susceptible)”疾病传播模型，考虑了节点会通过邻居的感染状况而出现警惕状态，而警觉态易感者被感染的概率显然和易感态不同，提出了S(susceptible)-A(aware)-I(infected)-S(susceptible)”模型，但其模型的研究局限于单个网络，没有考虑警惕信息的传播问题；文献[16]又研究了信息传播对疾病传播的影响，并找出在不同网络拓扑下最理想的信息传播机制；文献[17]在双层网络中研究疾病和信息两类传播动力学的相互作用，揭示信息传播对疾病传播及传播阈值的影响；文献[18]进一步研究了一种局部警觉控制传染模型(LACS)，其中当节点的警惕邻居数目与信息层节点度的比值达到局部警惕率或已被疾病感染，才能变成警惕态传播警惕信息；文献[19]研究了双层网络上具有自激发和扩散机制的警觉行为对传播动力学的影响；文献[20]考虑了双层网络上个体的异质性对警惕信息传播动力学的影响等。

之前基于双层网络对疾病传播与警觉意识扩散的研究多存在一个普遍性假设：在同一时刻警觉意识先传播，疾病后传播。虽然信息传播途径广一些，传播也更加便利一些，但是并非所有情况都如此。比如有些疾病虽然已经在人群中传播，但由于疾病的外部表现不容易被发现或者危险性没有引起充分注意，可能导致警觉不能快速传播。再比如，对于有些疾病而言，感染疾病的人不太愿意告诉他人自己的得病情况(比如性病等)，因此警觉也不能快速传播。故与之前的研究都不同，本文摒弃之前的假设，而是认为警觉意识与疾病的传播是不分先后次序的，进而比较两种机制对传播阈值和传播范围的影响。

1 UAU-SIS 模型

文献[17]考虑到疾病的爆发会引发警觉意识的传播，而且两种传播动力学的传播载体往往不同，因此基于双层网络提出经典的UAU-SIS 模型。

双层网络是指警觉意识传播的虚拟层和疾病传播的接触层，它们的邻接矩阵分别为 (aij)N×N和(bij)N×N，其中 N表示网络的节点数。类似于传统的SIS 疾病传播过程，虚拟层进行警觉意识传播U(unaware)-A(aware)-U(unawre)。按照对现存疾病风险是否有警觉意识，节点分为无警觉态(U)和警觉态(A)。虚拟层中处于警觉态的节点以概率 λ扩散警觉行为，而且无警觉的节点一旦感染自动变为警觉态。处于警觉态的节点又会以概率 δ忘记此信息，再次成为无警觉态。

接触层是疾病传播过程(SIS)，节点分为易感态(S)和感染态(I)。记无警觉态被感染率为 βU，警觉态感染率为 βA，感染恢复率为µ。因为无警觉态节点不知道疾病的信息，因而没有采取相应的保护措施，而警觉态节点了解到疾病的风险，通过一些自我保护措施(如减少外出、加强卫生等)，所以减少了被感染的几率。假设警觉态通过一个因子 γ来降低感染，记 βA=γ βU，其中0 ⩽γ ⩽1。这种双层网络上两种动力学相互作用的示意图如图1 所示，上层是警觉意识传播的虚拟层，节点分为无警觉态(U)和警觉态(A)；下层是疾病传播的接触层，节点分为易感态(S)和感染态(I)。

图1 双层网络上两种动力学相互作用的示意图

2 理论分析

下面将分析双层网络中信息与疾病的传播次序性对传播动力学的影响。

2.1 ordered model 理论分析

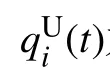
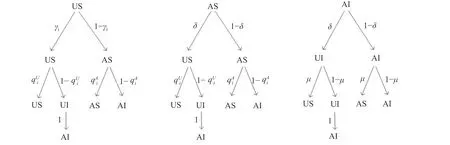
图2 ordered model 中每个时步节点各状态的概率转变树图

2.2 concurrent model 理论分析

文献[17]的研究以及基于此工作的推广都存在一个假设：在同一时刻警觉意识先传播，疾病后传播。虽然信息传播途径更便利一些，但在有些情况下，这种人为规定警觉传播的优先性是欠妥的，因为只有疾病发生了，警觉意识才会传播，另外，当人们没有充分意识到疾病的风险时，警觉意识的传播也未必快于疾病传播。故与之前的研究都不同，本文摒弃之前的假设，而是认为警觉意识与疾病的传播是不分先后次序的，提出一种不考虑传播次序的模型(简称为concurrent model)。

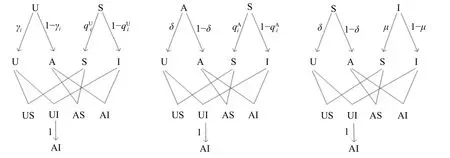
图3 concurrent model 中每个时步节点各状态的概率转变树图

根据图3 的概率转移图并结合马尔可夫链方法[17-19]，可以列出如下马尔可夫方程：

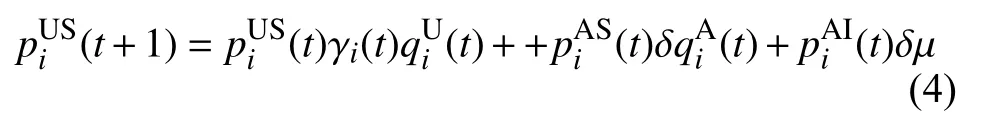
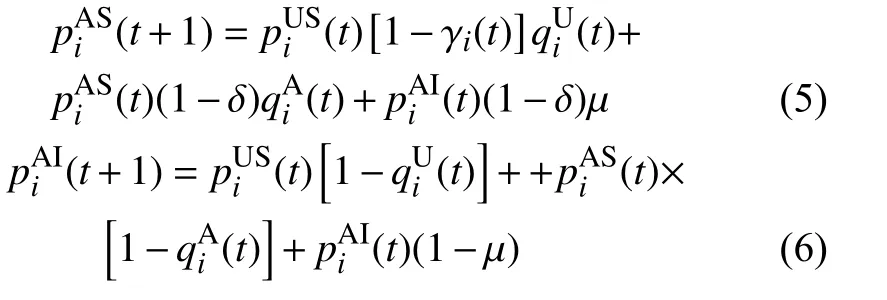
从式(10)～式(12)可以得出，传播阈值依赖于实际接触层的网络结构 (bij)N×N、参数 γ以及警觉密度 ρA。其中 ρA是由信息层网络结构、传播率 λ以及恢复率 δ等进一步确定的。故传播阈值受到双层网络结构、警觉意识的传播率等因素的影响。同时研究结果表明，两种模型得到的传播阈值是相同的。

3 数值模拟与分析

为验证本文的理论结果，建立一个节点数为2 000、度分布为p(k)～k−2.5的配置网络为接触层(bij)N×N，在接触层上增加800 条随机边(无重边)得到虚拟接触层 (aij)N×N。首先，将无序的马尔可夫链方法(MMCA)和数值模拟(MC)的结果进行比较，如图4 所示，其中初始感染种子为0.2，λ=0.15， δ =0.6 ， µ=0.4。从图4 可以发现两者拟合很好，进而验证了本文基于MMCA 的理论分析的有效性。

图4 马尔可夫链方法(MMCA)和数值模拟(MC)方法的对比

图5 在不同的警惕恢复率δ 和疾病恢复率µ 下，βc随 λ 的变化图

进一步给出在不同的警觉意识传播率 λ下，感染范围 ρI随着感染传播率 β的变化图，并在每个子图中插入对应的警觉意识传播范围 ρA随感染传播率 β的变化，如图6 所示，其中初始感染种子为0.2， δ=0.6 ， µ=0.4。可以发现：1) 当警觉意识传播率λ 固定时，随着感染率 β增大，感染范围 ρI显然会增大，而感染者会自动成为警惕态促进警觉信息传播，从而警觉范围 ρA增大；2) 当警觉意识传播率 λ较小的时候，从图6a、6b 和6c 中可以观察到，无序模型(con)对应的感染范围小于有序模型(ordered)对应的感染范围，但是随着警觉意识传播率的增加，从图6d、6e 和6f 中可以观察到，结果会发生反转，即无序性模型对应的疾病感染传范围会逐渐大于有序性模型；3) 有序模型(ordered)对应的警觉传播范围 ρA总是大于无序模型(con)对应的警觉传播范围，对于这种现象需要分为两种情况加以解释：当 λ较小的时候，节点的警觉态主要是因为被感染自动变为警觉态，而有序模型(con)感染范围较大一些，所以其警觉范围也更大一些；当λ较大的时候，节点大部分处于警觉状态，因为有序模型先在虚拟层进行警觉意识传播，故会有一部分节点先恢复成未警觉状态，增加了这部分节点的感染率，节点感染会立马警觉，从而导致恢复成未警觉状态节点在同一个时刻更容易变为警觉态，所以有序模型的警觉范围依然大于无序的。

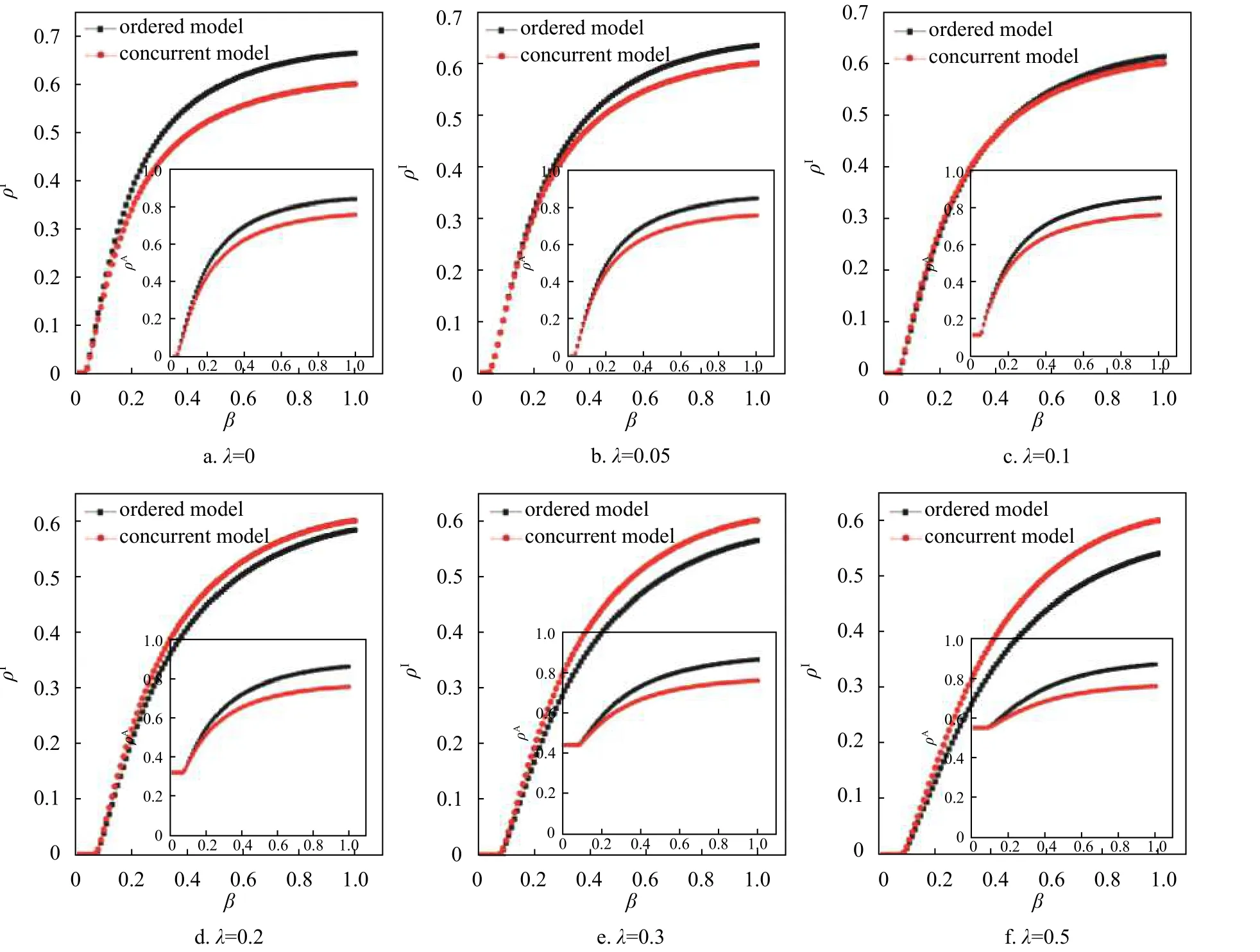
图6 在不同的警觉意识传播率λ 下，con 与ordered 中感染范围 ρI 随 β的变化图

图6 的结论3)表明：无论λ 取何值，有序模型对应的警觉传播范围 ρA总是大于无序模型对应的警觉传播范围。但是结论2)却表明： λ较小的时候有序模型的感染范围 ρI会较大一些；相反的，当λ 较大的时候有序模型的感染范围 ρI会较小一些。即，不能简单地认为警觉传播范围大的模型对应的疾病传播范围一定更小。这是因为：当λ 较小时，虽然有序模型对应的警觉传播范围大于无序模型对应的警觉传播范围，但是此时两者的警觉范围都比较小。对于有序模型而言，当进行疾病传播的时候，上一步的警觉者还没有通过虚拟层大范围扩散就又变回为未警觉态，从而导致有序模型对应的感染范围更广；当λ 较大时，两个模型对应的警觉范围都很大，而有序模型先通过虚拟层进行警觉意识传播，故会进一步增大警觉传播范围，而警觉态节点会降低自身的感染率，从而有序模型对应的感染范围就会较小一些。

为了进一步验证上述结论是否具有一般性，本文用ER 随机网络生成双层网络模型[21]，首先生成一个节点数为2 000、平均度⟨ k⟩=5的随机网络，作为接触层 (bij)N×N，然后在接触层上增加800 条随机边(无重边)得到虚拟接触层 (aij)N×N。进一步给出在不同的警觉意识传播率 λ下，感染范围 ρI随着感染传播率 β的变化图，并在每个子图中插入对应的警觉意识传播范围 ρA随着感染传播率 β的变化图，如图7 所示，其中初始感染种子为0.2，δ=0.6 ，µ =0.4。可以发现，图7 和图6 具有相同的现象，从而验证了结论的普适性。

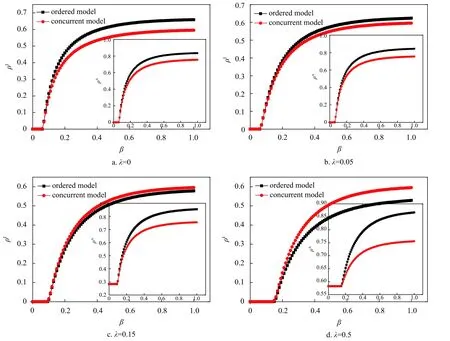
图7 在不同的警觉意识传播率λ 下，con 与ordered 中感染范围 ρI 随 β的变化图

4 结 束 语

本文提出不考虑传播次序的模型，即警觉意识与疾病同时传播。通过理论分析和数值模拟发现，感染范围和阈值不仅依赖于双层网络结构而且受警觉信息传播的影响。与之前的模型进行对比发现：信息与疾病的传播次序不影响疾病的传播阈值，但会影响两种传播的动力学传播范围。虽然无序模型对应的警觉传播范围总是小于有序模型对应的警觉传播范围，但却会对疾病传播范围有截然不同的影响：在警觉意识传播率较小的时候，有序模型导致警觉态节点没有大范围传播就变为未警觉态，从而导致疾病传播范围增加；而当警觉意识传播率较大的时候，有序模型保证警觉意识在虚拟层更大范围扩散，从而更有效控制疾病在物理层的扩散。本文的研究工作表明：当基于双层网络研究疾病和意识传播耦合作用时需要根据问题背景设定相应的模型并进行分析，否则可能会导致错误的结果。同时本文的研究工作也丰富了多层网络动力学的研究结果。

本文的研究工作得到安徽科技学院人才引进项目(100005)的支持，在此深表感谢！