基于无衍射光莫尔条纹的轴锥透镜锥角测量方法

杨练根，刘 凡，冉晶晶，翟中生

（1. 湖北工业大学 机械工程学院，湖北 武汉 430068；2. 湖北省现代制造质量工程重点实验室，湖北 武汉 430068）

引言

轴锥透镜为任一形状回转体，一侧为平面，另一侧为圆锥面[1]。不同于透镜汇聚于一点的成像方式，经轴锥透镜的光束在传输过程中表现出线焦特性，即光束高度约束在以中心轴线为基准的局部区域内，且不受衍射影响，具有中心光斑强度高、方向性好、准直距离长以及自修复特性等特点[2]。由于其独特的光学特性，广泛应用于无衍射光生成、光学成像系统、瞳孔整形、光学测试、激光束整形、自由空间光通信、飞秒激光加工、光互联和精密准直、精密光学检测等领域[3-6]。

在轴锥透镜的实际应用中，需要提前精确获取锥角参数，因此，对锥角有严格的测量要求。例如，为了保证光刻照明系统中的瞳孔能量平衡，瞳孔整形单元中一对轴棱锥透镜的锥角精度要求应在±30″以内。

近年来，各种锥角测量方法得到了发展，其中坐标测量机（CMM）就是一种常用的方法，但这种接触测量方式可能造成轴锥透镜表面损伤，影响其光学特性，并且较为耗时。接触测量方式可以用于验证非接触方法的测量结果。除了接触测量技术，很多非接触测量方法也用于测量轴锥透镜的锥角。De Angelis 等人[7]提出了双光束剪切干涉法测量轴锥透镜的锥角，此方法仅适用于小基准角的测量。Fantonetal[8]用马赫曾德干涉仪测试轴锥透镜表面，该方法结合一个精确的方形沿切向旋转扫描获得锥角。然而，上述两种方法的设置都很复杂。此外，这些方法在在测量锥角范围上存在局限性。Ma 等人[9]用计算机生成的全息图（CGH）测量锥角，测量装置设置很简单，但是CGH 通常是复杂、昂贵和耗时的。Zhang J[10]提出一种基于双波长色散的方法，测量装置紧凑，容易调节，然而忽略了不同波长对于成像透镜焦点距离的影响，不能满足大多数现代应用要求。Zhang[11]提出了一种基于自准直光路的轴锥透镜锥角的测量方法，但测量时需要实时调整记录平行板和经纬仪与轴锥透镜之间的偏角，另外，为提高测量分辨率延长了整体光路，增加了测量难度。

本文提出一种基于无衍射光莫尔条纹测量方法，经分光合束的两无衍射光束相互干涉叠加后形成一定数目的莫尔条纹。根据两无衍射光束中心光斑间距、莫尔条纹数量、激光波长、轴锥透镜折射率可以计算出锥角值。实验结果表明，本方法具有较高的锥角测量精度。

1 轴锥透镜锥角测量系统设计

1.1 轴锥透镜锥角测量系统硬件构成

本文提出的测量方法的光路结构示意图如图1所示。测量装置由激光器、准直扩束镜、待测轴锥透镜、分束器、反射镜、二维平移台、以及与计算机相连的图像传感器组成。上述装置固定安装在实验平台上，其中反射镜2 安装在二维平移台上。实际测量时，反射镜2 能够沿光路传播方向进行水平位移，待测轴锥透镜锥角可以为任意角度。

1.2 轴锥透镜锥角测量系统工作原理

图 1 测量光路结构示意图Fig. 1 Structure diagram of measuring optical path

轴锥透镜锥角测量系统工作原理为：激光器发出的光经准直扩束后垂直入射轴锥透镜，在轴锥透镜后形成零阶贝塞尔形状的同心圆环（无衍射光），其仿真图如图2（a）所示。图1 中分束器1 将无衍射光分为两束衍射光，分别称为参考光束和测量光束，其中参考光束经反射镜1 和分束器2 后垂直入射到图像传感器上形成无衍射光，其中心光斑位置不变称为参考点；测量光束经反射镜2 和分束器2 后垂直入射到图像传感器上形成测量点，这两束无衍射光相互干涉形成莫尔条纹，其Matlab仿真图如图2（b）所示。

图 2 仿真示意图Fig. 2 Schematic diagram of simulation

其中测量点受反射镜2 位置的影响而发生改变，通过调节二维平移台完成调整参考点与测量点中心距离的任务。每一次中心距离改变，对应的莫尔条纹数发生变化，图像传感器完成对不同莫尔条纹数干涉图像采集。采集的图像由计算机完成图像处理并计算相关实验数据，最终得到轴锥透镜锥角计算结果。

通过轴棱锥透镜传输的激光束向2 个方向偏转，因此，需要调整反射镜。为了从一维分析中获得精确的结果，激光光束须严格平行于轴锥透镜光轴方向。一是经扩束准直的激光束垂直入射到轴锥透镜的平面上，调整轴锥透镜位置使激光束通过锥体顶点传输，通过判断设置在轴锥透镜后方白屏上是否出现中心光斑光强均匀的同心圆，确定激光束是否通过锥形顶点传输；二是经反射镜反射回来的测量光束与参考光束在分束器后表面合束产生干涉，其中参考点在图像传感器上位置是固定的，通过调整反射镜2 姿态对反射点位置进行微调，使图像传感器上出现干涉明显的莫尔条纹。三是沿光束传播方向水平移动反射镜2，以实现对参考点与测量点之间中心距离的调节，采集多个不同中心距离下的莫尔条纹，进而测得轴锥透镜某些轮廓线下的锥角平均值。

2 轴锥透镜锥角计算方法

2.1 不同位置两条无衍射光干涉叠加

设参考光束和测量光束光程分别为Z1和Z2，在图像传感器平面上的极坐标分别为r1和r2，r 为光束透过轴锥透镜半径，两束无衍射光在图像传感器上的复合振幅为

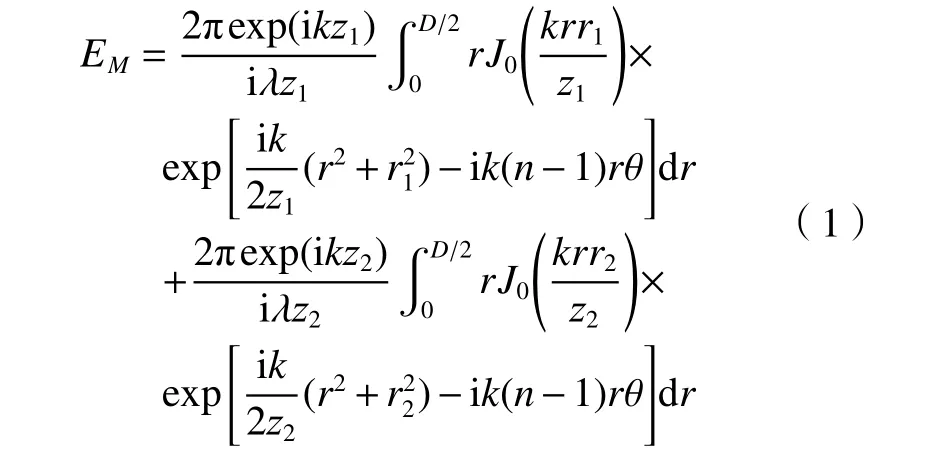
根据上式，利用稳相法[12]可得光强近似为

由公式（2）可知，其光强分布可以理解为2 个不同位置的零阶贝塞尔函数的叠加，其干涉图样表现为明暗条纹等距相间分布的同心圆环[13]。两束无衍射光的干涉场可视为2 个等间距的同心圆环光栅的叠加。

其中零阶贝塞尔函数的零点近似可以表示为[14]

对（4）式作进一步推导，得到同心圆环两相邻光栅间距d 为

2.2 锥角公式推导

根据文献[15]可知，两无衍射光束叠加形成的莫尔条纹轨迹表现为一系列对称分布的双曲线簇，其条纹分布及数量受两光斑中心间距影响。通过对中心间距 D与双曲线渐近线与两光斑中心之间连线夹角 α关系进行推导，可得到：

式中k 为莫尔条纹族对应的序列数，由公式（5）可知，光斑中心间距与光束光程无关。即在无衍射光有效传播距离内，光栅间距为定值。设 D=nd，n 为正整数，结合（5）式可得：

由（7）式可知，当k=0， α=90°；当k=n， α=0°。表明 α在0°～90°内，对应的莫尔条纹数与光栅中心间距数一致。则总体圆周上莫尔条纹数N 与中心间距数n 呈4 倍线性关系，即N=4n。

利用Matlab 对不同间距数下莫尔条纹数进行仿真验证，得到的结果如图3 所示。由图3 可以看出， α在0°～90°内，莫尔条纹族最大序数始终等于对应间距数，与上述推论结果保持一致。明显地，与排列紧凑的同心圆环明暗条纹相比，呈发散分布的双曲线莫尔条纹更易被识别，采集莫尔条纹数可以实现对间距数的计量。

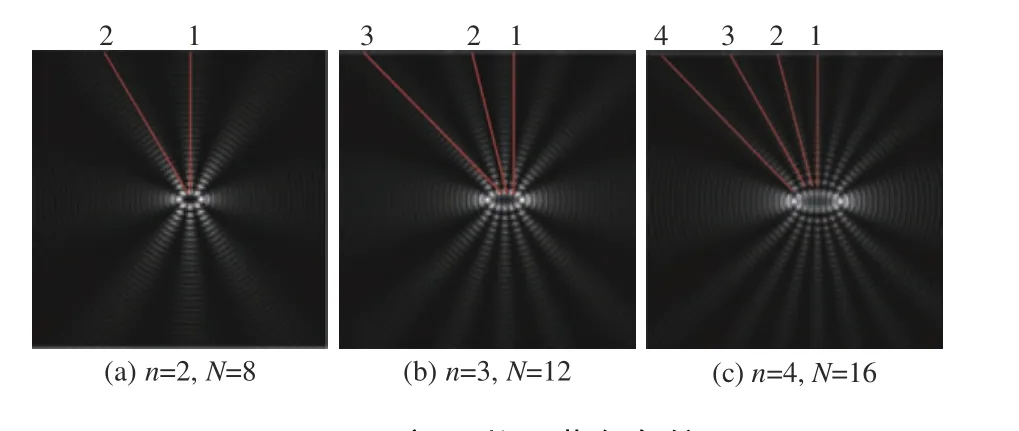
图 3 不同间距数下莫尔条纹图Fig. 3 Moire fringe pattern with different spacings

莫尔条纹数量与两同心圆环光栅中心间距及中心距离关系为

将图像传感器视场平面作为坐标平面，连续2 个像素点间距视为最小单位长度。以视场左上角顶点作为坐标原点，记录参考点和测量点中心位置，其中参考点和测量点中心位置分别对应于两同心圆环光栅中心。根据算法直接确定参考点及测量点中心坐标（x0，y0）和（x1，y1），中心距离D 表示为

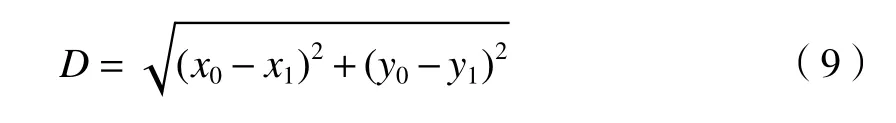
通过图像处理程序实现莫尔条纹的计数，结合像素坐标计算得到中心距离，完成对轴锥透镜锥角 θ求解。根据公式（5）和（8），轴锥透镜锥角 θ可以表示为

3 实验结果及分析

实验所选用激光器为大恒光电DH-HN 系列氦氖激光器，输出功率大于1.8 mW，波长 λ为632.8 nm，扩束镜头扩束范围比为5x～10x。分束器及反射镜材料均为K9，分束器尺寸 为25.4 mm ×2 5.4 mm×25.4 mm，反射镜直径为25.4 mm，其表面反射率大于99.5%。图像传感器像元尺寸为5.2 μm ×5.2 μm。结合公式（10）以及图像传感器像元分辨率，带入前后坐标参数最小差值，得到理论测量分辨率优于0.72″。实际实验中直接将所述激光器作为光源，会因为入射图像传感器激光光束亮度过高使得采集的莫尔条纹图泛白，进而导致测量失效。在实际光路中引入光衰减片对激光光束亮度进行调节，得到明暗对比明显的莫尔条纹图，以方便下一步的图像处理。

本文以THORLABS 公司生产的轴锥透镜作为测量对象，相关数据如下：材质为紫外熔融石英，锥镜折射率n=1.46，半径r=12.7 mm，锥角θ=0.5°±0.01°，即锥角公差为72″。二维平移台为高精密线性平移台，位移最小分辨率为5 μm，行程为±12.5 mm。选取莫尔条纹数为8、12、16、20、24 和28 进行实验，同时记录图像传感器中莫尔条纹图像以及所述平移台位移行程。图像传感器采集的图像如图4所示。

图 4 不同位移下莫尔条纹图Fig. 4 Moire fringe pattern under different displacements

通过图像传感器记录的图像信息，可以确定对应莫尔条纹数下参考点中心及测量点中心的位置，结果如表1 所示。根据公式（9）计算的参考点与测量点中心距离，结合已知激光器及轴锥透镜参数带入公式（10），得到锥角测量结果如图5（a）所示，平均角度为0.490 7°。其中图5（b）给出了本测量系统12 次重复实验的结果，锥角测量结果的均值为0.490 8°，重复性为0.86″。为验证本测量方法的精度，采用Hexagon 公司的Leitz Infinity 三坐标测量机进行比较。该测量机的最小测量分辨率为0.1 μm，空间精度为0.3 + L/1000 μm，因其测量精度很高，故用其测量轴锥棱镜锥角的测量误差几乎可以忽略。如图6 所示，选取轴锥透镜某一轮廓的母线上两点作为探头测量点，测量12 个不同位置母线，其中相邻母线角度分布间距为30°，得到该轴锥透镜的锥角平均值为0.493 5°。与三坐标测量机测量结果的差值为−0.002 7°，即−9.72″，可认为本文所提出的测量方法的相对测量误差近似为0.54%。

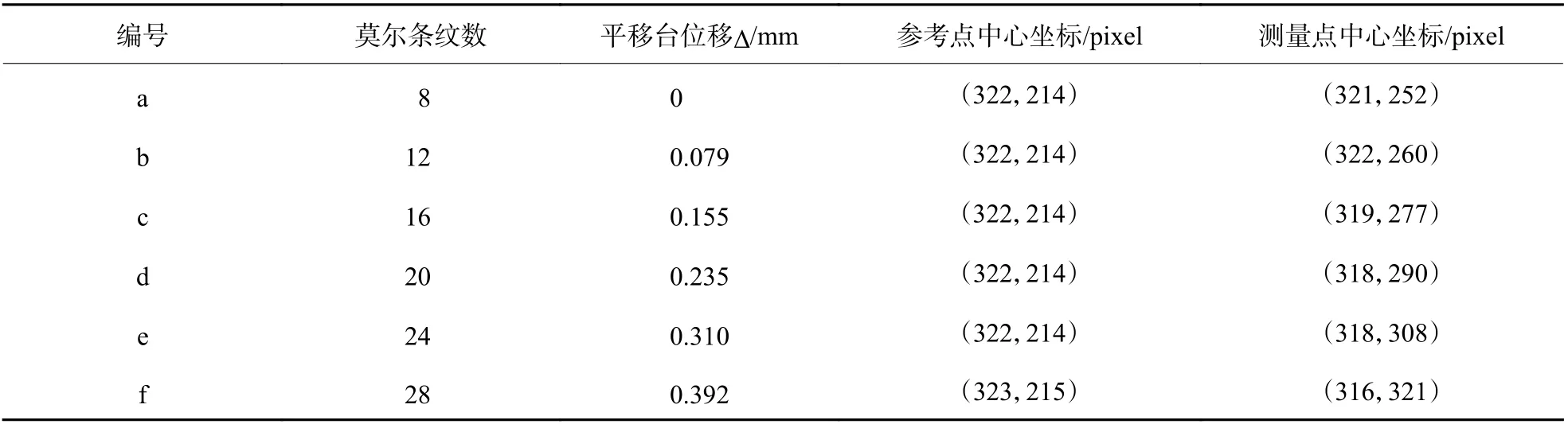
表 1 测量结果Table 1 Measurement results

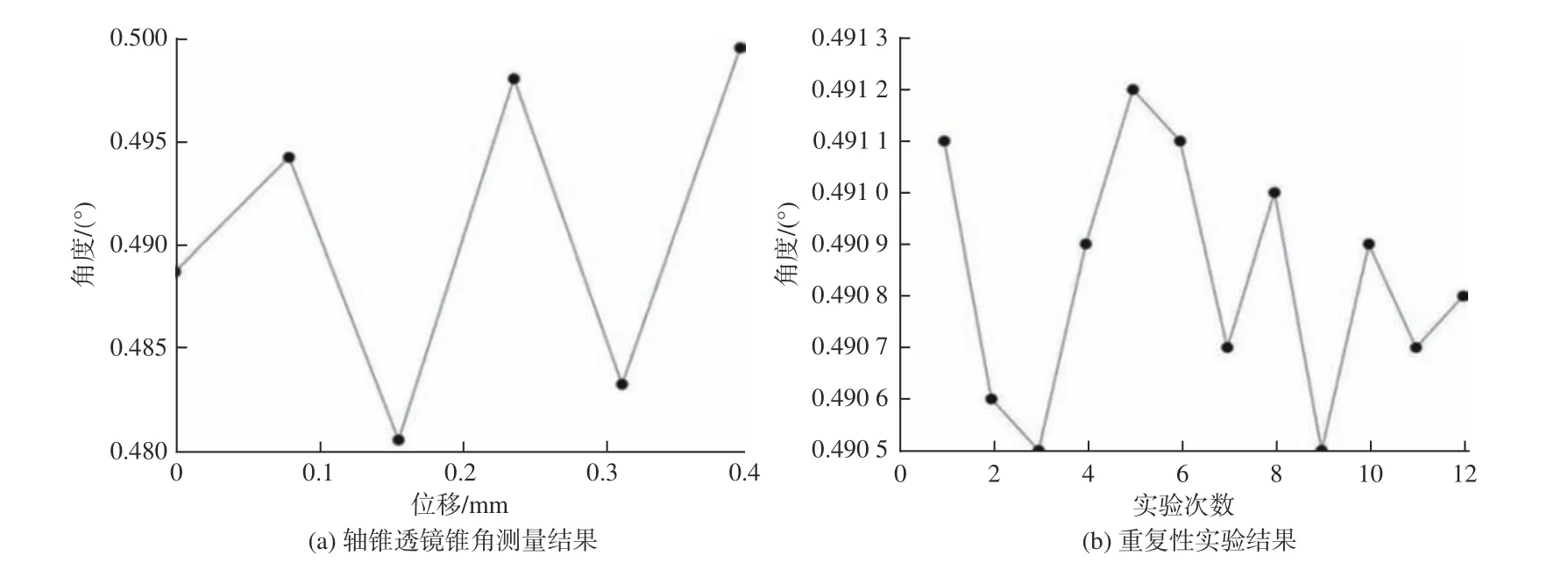
图 5 轴锥透镜锥角测量结果及重复性试验Fig. 5 Axicon cone angle measurement results and repeatability test

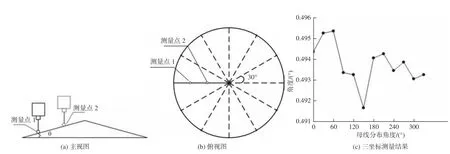
图 6 三坐标测量机测量方式示意图及测量结果Fig. 6 Schematic diagram and measurement results of CMM measurement mode

4 结论

本文提出的基于无衍射光莫尔条纹的轴锥透镜锥角测量方法，以无衍射光同心圆环间距与轴锥镜锥角满足确定关系式为切入点，将待测轴锥镜自生成无衍射光引入到测量系统中，简化了测量光路。同时对双无衍射光干涉形成的莫尔条纹数与两中心光斑间距数关系进行推导并仿真验证，结果表明两者存在确定的线性关系，通过采集相对易识别的莫尔条纹数完成对间距数的计量。另外，根据无衍射光同心圆环间距大小不随光程而改变特点，实现不同光程下，即两束无衍射中心光斑在不同中心距离下轴锥镜锥角的测量，提高了系统测量精度。本系统测量的轴锥镜锥角与CMM 测量结果相比，测量误差为−9.72″，仅为锥角公差1/8，重复性为0.86″，完全满足对锥角的测量要求。该方法只需对轴锥镜生成的无衍射光进行简单的分光合束，仅使用单一波长光源，无需设置如全息图、高精度方形、电子经纬仪等测量元件，与其他测量方法相比，本方法简单、成本低、可靠性高。