LED全反射透镜计算新方法

周士康，杜 金，陈春根

(上海三思电子工程有限公司，上海 201199)

引言

全反射(TIR)透镜具有其他类型透镜无法达到的高效率。有两个原因造成了TIR透镜的高效率，其一是这种透镜可以将LED发出的全部180°的光收集并射出去，其二是采用了反射率近100%的全反射面。

目前大多数LED为荧光粉转换白光LED，而由于荧光粉和芯片的位置有偏移，蓝光和黄光经过透镜出射后的方向也将有偏移，使得照明产生了色差。不过由于这一偏移的方向在反射时和透射时相反，因此当透镜中既有反射又有透射时上述偏离会在一定程度上抵消，这使得TIR透镜会比其他类型的透镜的色差小些。

正是由于TIR透镜以上独特的光学性能，才使得TIR透镜成为目前市场上使用量最大的LED透镜。透镜设计时，厂家往往是选择一个已有的透镜，用商用模拟软件对透镜的形状加以修改。由于现有的计算方法[1-7]大多比较复杂，用户需要一个方便的计算透镜形状的方法。本文用光通量线(LFR)方法[8]较好地解决了LED的TIR透镜的计算问题，没有复杂的计算，而且可以用在许多场合。

1 透镜表面形状计算的光通量线方法

1.1 求单个小面的基本方法

可以由两条LFR依据折射定律计算得到一个透镜的小表面。用图形表示如图1所示，由入射线方向、折射线方向用折射定律求得折射小面法线的方向。其中偏折角是指光线的入射角和折射角之差，透镜表面的作用就是“偏折”光线。也就是已知折射点以及入射和出射两个角度，求得折射小面方向。而两组LFR将计算得到N个首尾相接的小面(折线)，当N很大时，折线就变成平滑曲线。

在本文的光通量线(LFR)方法[8]中，LFR既有各自的方向又有相同能量。这样，照度分布就成了LFR的密度分布，LFR密集的地方能量就大，照度就高，只要求得LFR的分布，就可求得该照度分布下的透镜形状，可以比较容易地处理预先给定的照度分布问题。本文也有给定表面求LFR方向的情况。此时就像常规情况那样，是已知折射点、入射线和折射面，求折射线方向。

1.2 求整个单面的方法

求整个表面的形状需要知道该面的所有入射线的位置和方向以及所有出射线的方向，但并不需要知道所有折射点的位置，只需要知道起始点的位置即可。因为用1.1的方法求得第1个小面后，再求该面和第2条入射线的交点就是第2小面的起始点，这样可以逐次求得全部小面，从而得到整个面，见文献[8]。

可见LFR方法求一个表面的关键是得到该表面所有入射线和出射线的角度，构成两个序列。

例如，设光从位于坐标原点的LED出发，12条入射LFR如左方的射线簇所示，已知右方的12条线的角度代表了出射线的方向，折射面的起始点在x=6，可以依次求得12个小面，如图2所示，求得的表面一般是一个自由曲面。这一过程很容易写成子程序，应用于所有面的计算。

正是因为LFR赋予了能量的属性，所以就可以由照度分布求得出射LFR的角度分布，这样才能事先给定照度分布来计算表面形状。此外，此方法的限定条件是被照明的尺度比透镜尺度大得多的情况，这样才能只关心出射光线的方向而不关心其落点。

图2 由两个方向序列求一个面

2 TIR准直透镜的计算

2.1 符号及分区

本文讨论的问题限定在具有5个光学面的TIR透镜。我们把透镜划分为两部分，A区有2透射面，B区有1个反射面和2个透射面，如图3所示。本文中使用的符号定义如下：

Na：A区光线数；

Nb：B区光线数；

N：光线总数，N=Na+Nb；

Io(α)：物方光强分布函数；

IM(β)：像方光强分布函数；

EM(β)：像方照度分布函数；

α1：A区中面1入射线角度序列(Na维)；

β2：A区中面2出射线角度序列(Na维)；

α3：B区中面3入射线角度序列(Nb维)；

β5：B区中面5出射线角度序列(Nb维)；

γ12：面1面2间的光线角度序列(Na维)；

γ34：面3面4间的光线角度序列(Nb维)；

γ45：面4面5间的光线角度(Nb维)；

SO：物方总能量；

SM：像方总能量。

以上定义使用的一般规则为：α代表入射线角度，β代表出射线角度，γ代表透镜内部光线角度，注意αβγ等代表的是多个数组成的序列。I为光强，E为照度，S为能量，O为物方，M为像方。阿拉伯数字代表表面的序数，其中α和α3共同组成透镜的入射线，β2和β5共同组成透镜的出射线。这里我们沿用了几何光学的物方(LED方)和像方(照明方)的概念。

第一个例子是一个如图3所示的最简单的平表面TIR准直透镜[9，10]。面5和面1重合，且垂直于光轴，面4为全反射面，其余各面均为透射面。

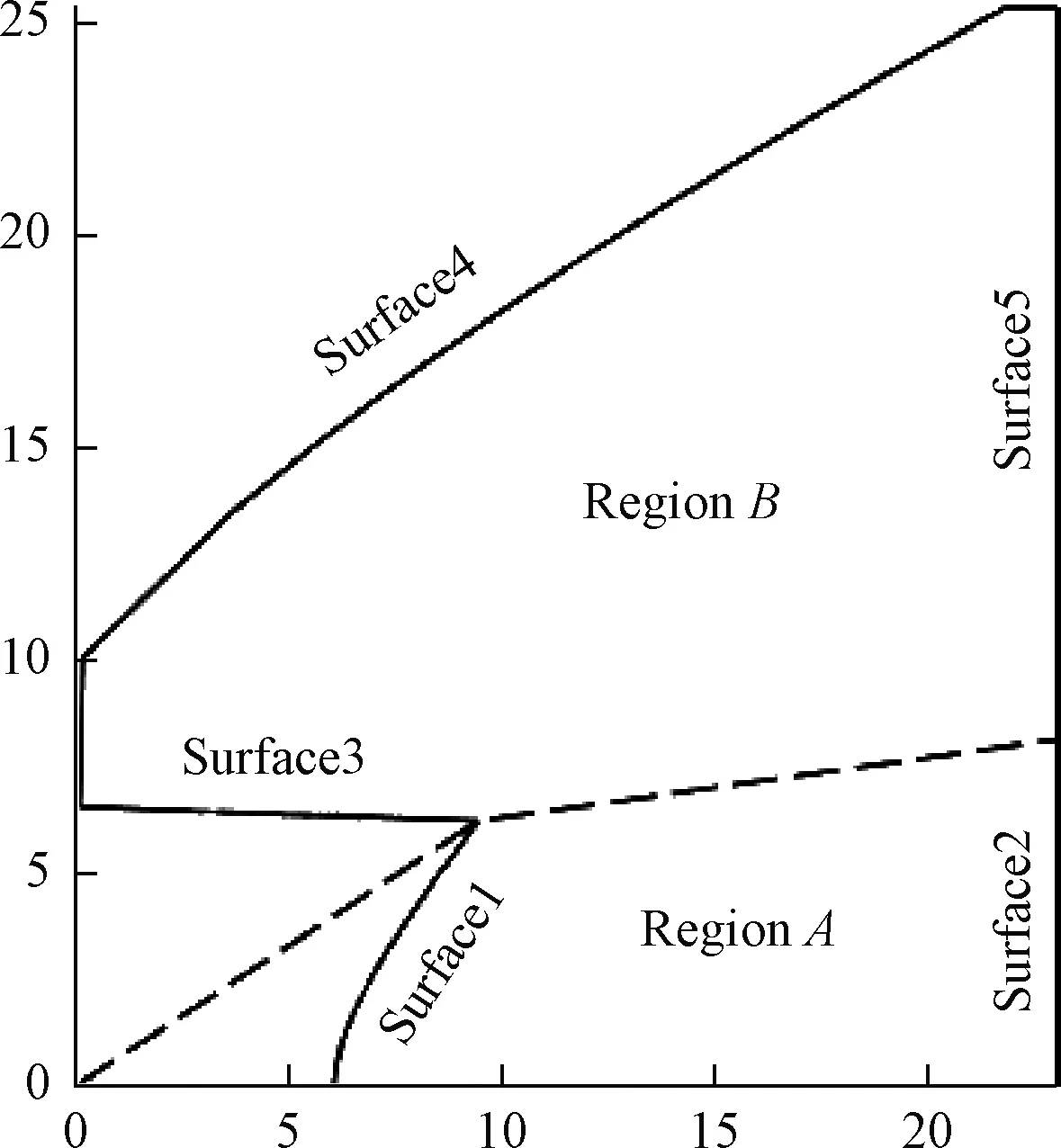
图3 平表面TIR透镜

2.2 求物方LFR分布

为了求得表面形状，我们需要求得该面的所有入射和出射LFR的角度。由于LED向某一方向发射的光通量正比于该方向的光强与立体角的乘积，因此可以即将光强分布曲线在整个发光角范围内积求得总光通量SO。再将SO等分成N份，让每一份的能量和方向用一条LFR来代表，这N份就给出了N条LFR。这就得到了既有相同能量又有方向的物方LFR方向的分布。

物方光强分布是已知的。以Osram WSAM和Cree 7090这两种LED为例，其光强分布可以是厂家给出的或测量得到的极坐标下的曲线，如图4所示，显然应该得到不同的LFR分布。

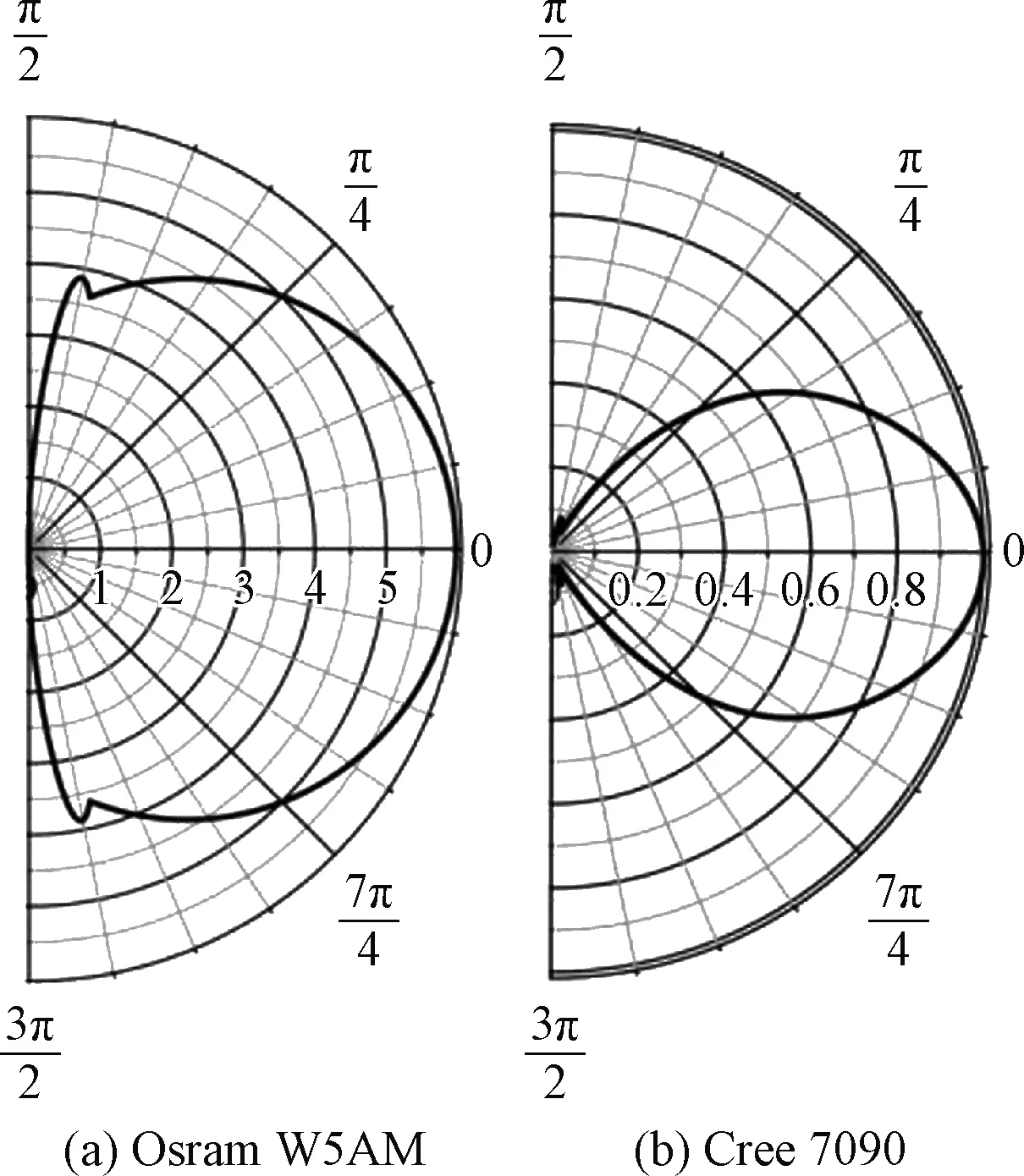
图4 LED光源的光强分布函数

现有的非成像光学设计方法[1-7]都是把LED看成是朗伯体，其光强分布为相同的余弦分布。而在LFR方法中，余弦分布只是一个特例，可见本文的方法更为广泛且精确。

本文用一个数学函数来表示LED的光强分布函数。这函数可以用常见的拟合方法来求，一般是一个分段函数，令其为I0(α)。

物方的总能量设为SO，它应正比于光强分布函数对全部角度的积分：

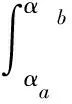
(1)

其中αa和αb为物方边缘光线的角度。把SO分为相等的N份，而每一份中有一条LFR，此LFR的方向αi是通过式(2)的N个方程来求得的。这样的方程用Maple或Matlab等数学工具很容易求解。

(2)

这就得到了物方LFR角度数列α=αi(i=1，…，N)：

α=(α1,α2，…，αN)

(3)

2.3 求像方LFR分布

由于我们不知道像方的光强分布IM(β)，只知道用户要求的照度分布EM(β)，因此像方的LFR计算和物方的略有不同。

对于平面被照明面，IM(β)与EM(β)有着确定的关系，可以由图5推得其关系式。图中O为LED的位置，设其法向沿直线OA，A为垂直被照明的位置。由照度的距离平方反比定律可知在被照明面上任一点B处的发光强度IM(β)应该为IM(β)=EM(β)·(OB)2=EM(β)·((OA)2+(OB)2)=EM(β)·(OA)2(1+tan2(β))∝EM(β)·(1+tan2(β))，其中1+tan2(β)就是像面为平面时照度与光强的关系因子。

图5 平面像面的照明示意图

有了IM(β)，就可以与物方的方法类似，以像方边缘光线的角度βa和βb为积分区间，由式(4)得到式(5)，从而求得像方光通量线的角度数列如式(6)所示。

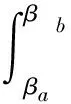
(4)

(5)

β=(β1,β2，…，βN)

(6)

于是就得到了式(3)的入射LFR角度分布α和出射LFR分布角度β，可以将两者建立一一对应的关系。

2.4 光通量线分区

得到式(3)和式(6)后，把它们各分成两部分。举例说明，令N=22，分为Na=12和Nb=10，α和β就各自分成了两部分，分属A和B两个区，这两部分比例将影响透镜的形状。

(7)

(8)

2.5 A区面1面2的计算

首先给定面1面2的起点，分别为光轴上的两个点x=6和x=23，其位置决定了TIR透镜的尺寸。在本文的特殊情况下，已知面2为垂直平面，出射为平行光，即β2=0, 因此有γ12=0。用2.2节的方法顺序计算得到面1的Na个小面，见图6。

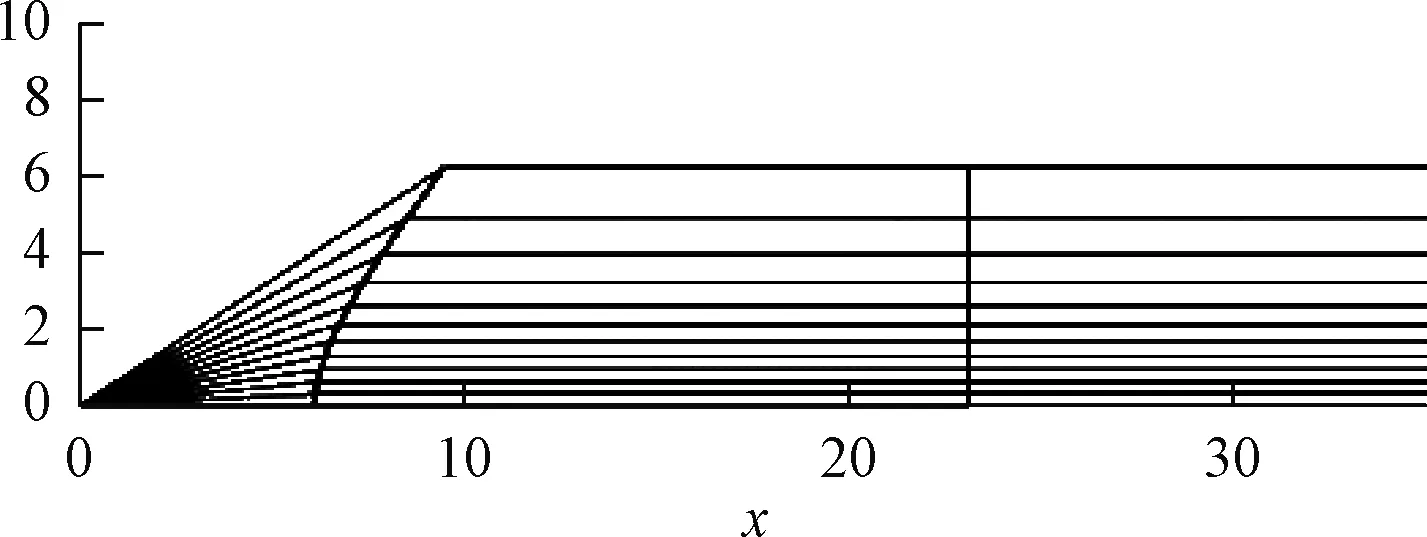
图6 A区表面的计算结果

在一般情况下，面1和面2的计算和一般双面透镜的计算是一样的[2]。为了同步计算两个面，引入表面的“偏折力”的概念[9]，其含义是表面偏折光线的能力。图1给出了偏折角的含义。令面1和面2的偏折力的权重分别为C1和C2，则由文献[11]中的方法可得透镜内部光通量线角度的数列为：

(9)

当C1=C2时，

(10)

γ12=(γ121,γ122，…，γ12Na)

(11)

这就得到了三个LFR角度数列：物方的数列、像方数列以及透镜内部LFR的角度数列。注意这三个数列中所有α1i都从原点出发，γ121从点x=6出发，β21从点x=23出发，得到面1面2的第1个小面后再用1.2节的方法得到面1面2的全部小面。

2.6 B区面3的计算

B区有三个待定面(面3面4面5)，只需要使其满足α3和β5这两个角度序列，因此可以在一定程度上选择面3的形状，常常用一条与水平轴线成一个小夹角的直线，这样有利于零件注塑时拔模，此时γ34可以方便地用常规折射定律得到，见图7。

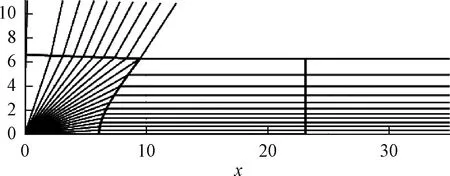
图7 面3为一斜线

2.7 B区反射面4和出射面5的计算

为了透镜边缘有一定厚度，可以选择面4的起点离面3的终点有一定距离。现在由于γ34已知，还需要知道γ45。在本例的简单情况下，输出平行光，即β5=0,γ45=0，这就可以用2.2节的方法依次求得面4的位置，结果是一个自由曲面，见图8。

图8 面4为自由曲面

用γ45=0和β5=0，虽然面5已知，仍然按照1.2节的方法求得面5为一个平面，见图9。最后结果见图10。

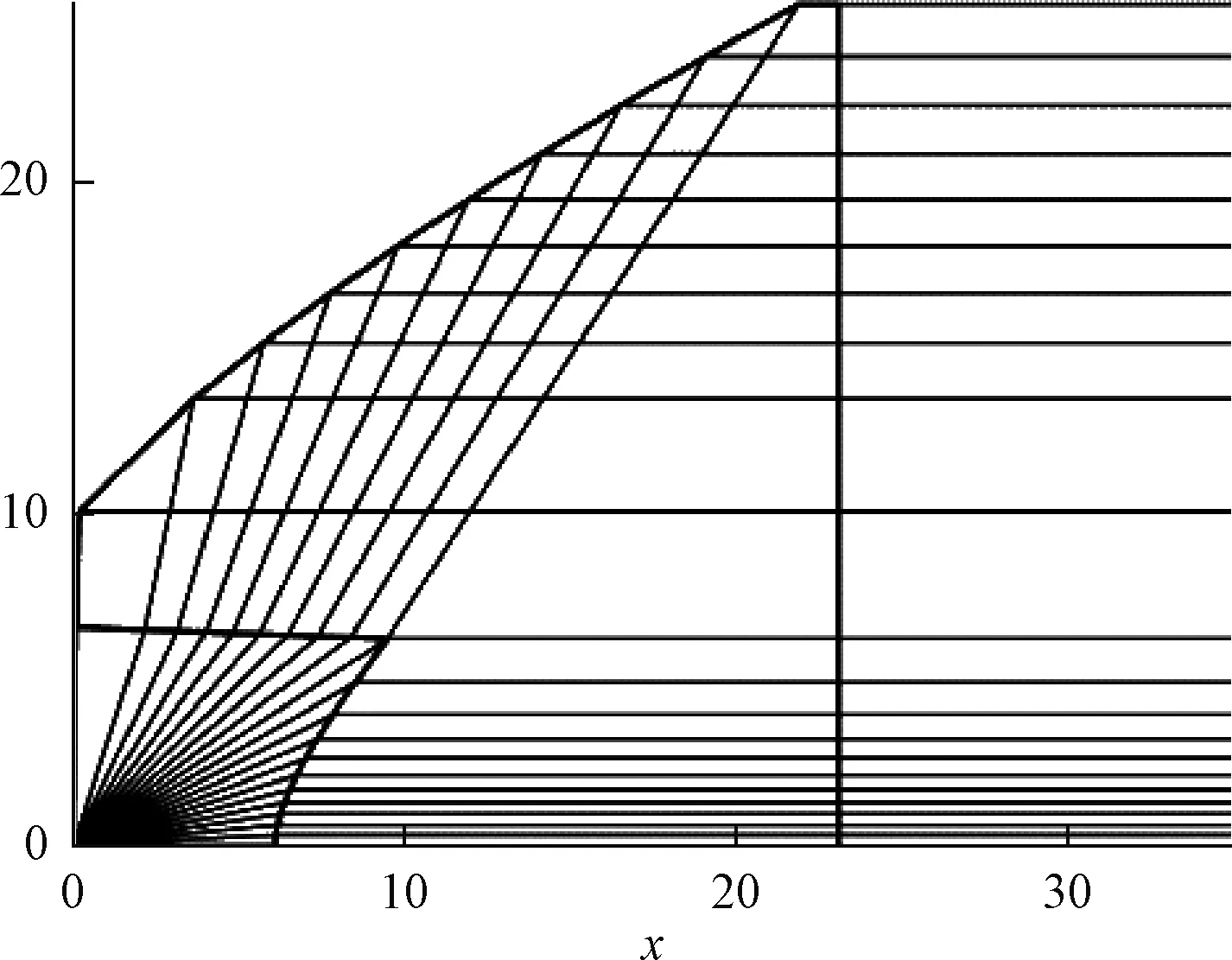
图9 面5为一垂线

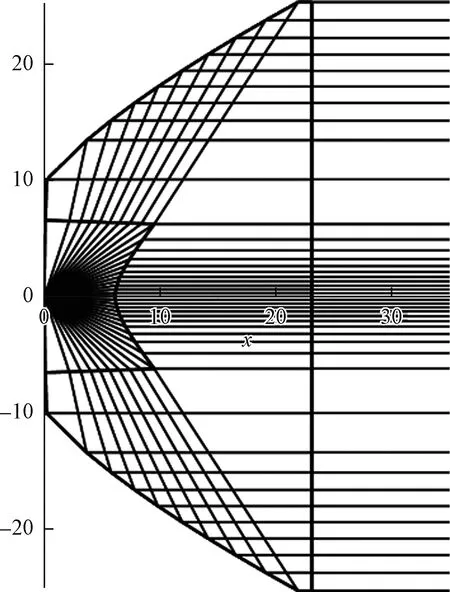
图10 平表面准直透镜最后计算结果

在本文的简单情况下，面2面3和面5都是给定的直线，但为了编写程序简单化，在实际情况下它们仍然是用由LFR的角度计算出来的，结果和给定的面完全一致。

在一般情况下，β5≠0,γ45≠0，还可令面5的起点离面2的终点有一定距离，并由式(9)的β5和γ45求得面5。

3 其他类型透镜

3.1 非准直透镜

本方法处理非准直透镜十分简单，这就是一般给定照度分布的透镜计算。这时β2，β5，γ12和γ45均不为0。用2.2节的方法可以求得像方LFR的分布β2和β5，然后用由常规折射定律计算得到γ12和γ45，再用同一程序计算，得到面2面5为平面。

此时，面2和面5的出射角度范围可以重合，也可以各自不同。这给设计带来了灵活性，也就是说，照明的要求可以由β2和β5的序列的分布协同来达到，这要结合A和B两区的分区情况及照度要求灵活掌握。

图11为平表面非准直透镜的一个例子。光束角为40°，N=22,Na=12,Nb=10,β2和β5的分布范围相重合。

图11 平表面光束角40°

3.2 非平表面透镜

为满足光学和结构上的一些要求，例如希望有更大的出射光束角，TIR透镜表面可以是非平面，这用本方法也易于解决。非平面表面的TIR透镜，也可以处理给定照度分布的情况，再结合选择不同的计算起点，可以得到多种类型的TIR透镜，下面只举其中的两个例子。

给定下列条件：β2≠0，β5≠0；β2和β5的范围重合；面5为直线；面5的起点和面2的终点重合；出射光束角为60°；N=22,Na=12,Nb=10；C1=C2。用2.5节的方法可以同步求得面1面2，C1，C2的变化还可以方便地改变面1面2的形状。图12是C1=C2时的计算结果，相比面2为平面的情况，这时面1的曲率半径较大，这将有利于加工，而且由于入射角相对于平表面的TIR透镜的要小，其Fresnal反射也小，从而杂散光也会变小[11]。

图12 凸表面TIR 透镜60°光束角

如果给定面5的起点和面2的终点不重合，则会得到图13的结果。这种透镜的优点是重量减少而且注塑后形变小，这在需要比较大的透镜时常常被使用。这里，为了控制透镜形状不致太大，还给定了γ34的范围，并使得面3为一个自由曲面。

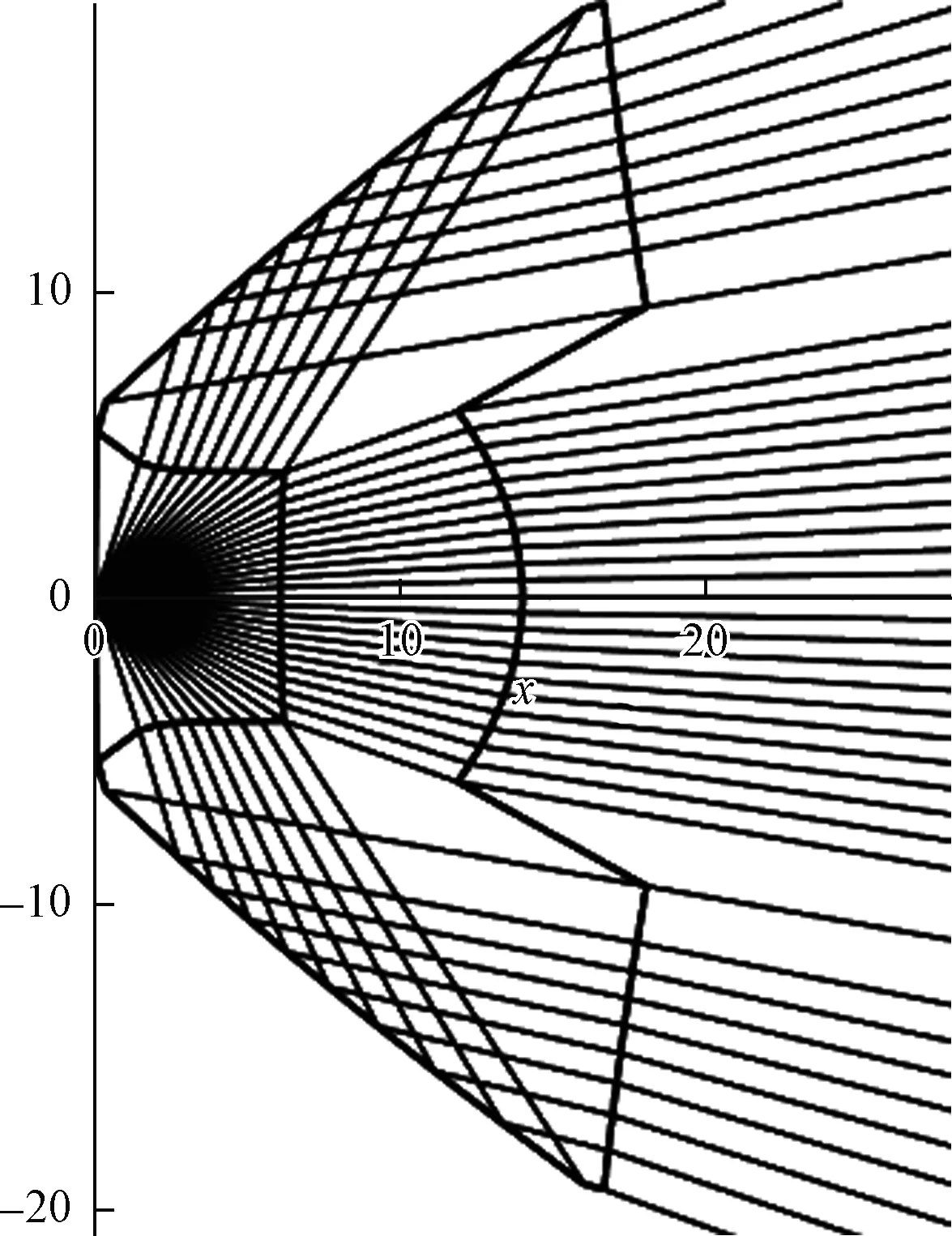
图13 一种下陷表面的TIR透镜

3.3 全景TIR透镜

如果计算时把类似图12的透镜对称轴旋转90°，就可以得到360°的TIR透镜。图14是一个机场用的障碍灯的计算结果，计算方法和上面的其实是一样的。这里透镜注塑时拔模的方向不同了，所有面都不是直线而是自由曲面，从而得到了十分紧凑的透镜形状。出射光强分布见图15，达到了全景照明的要求。

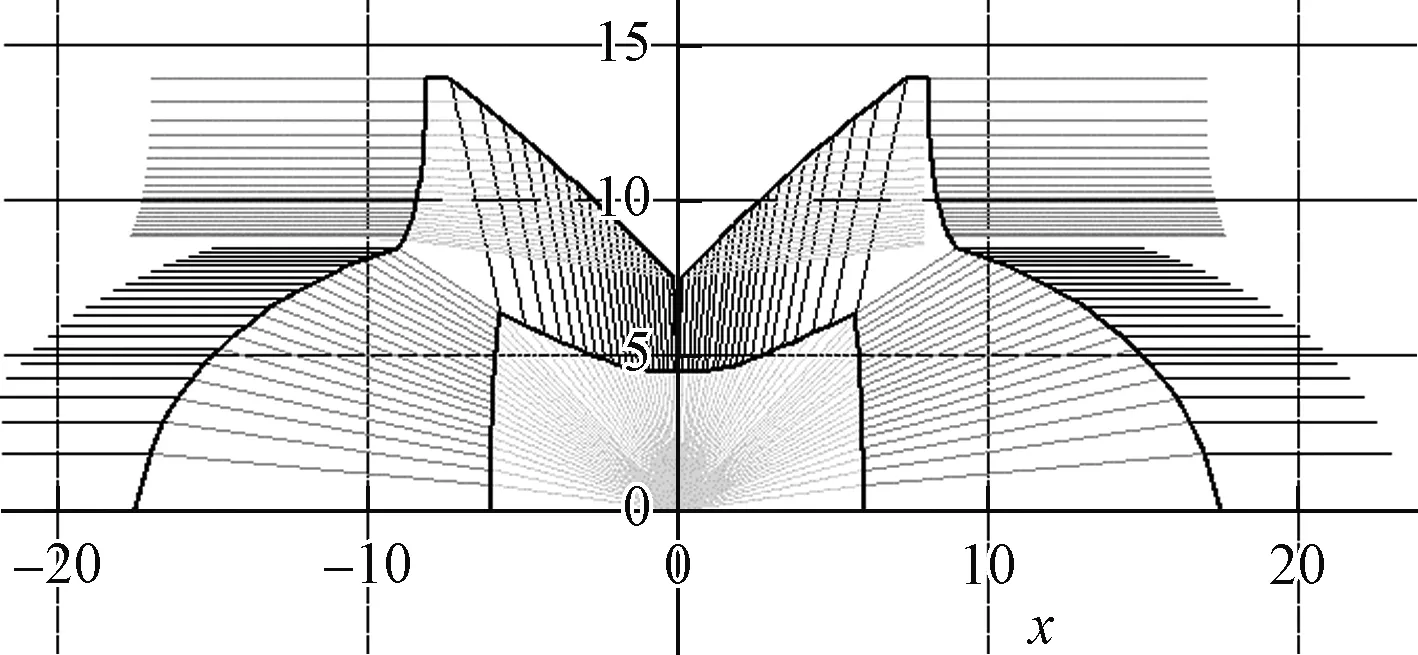
图14 机场障碍灯用的全景透镜

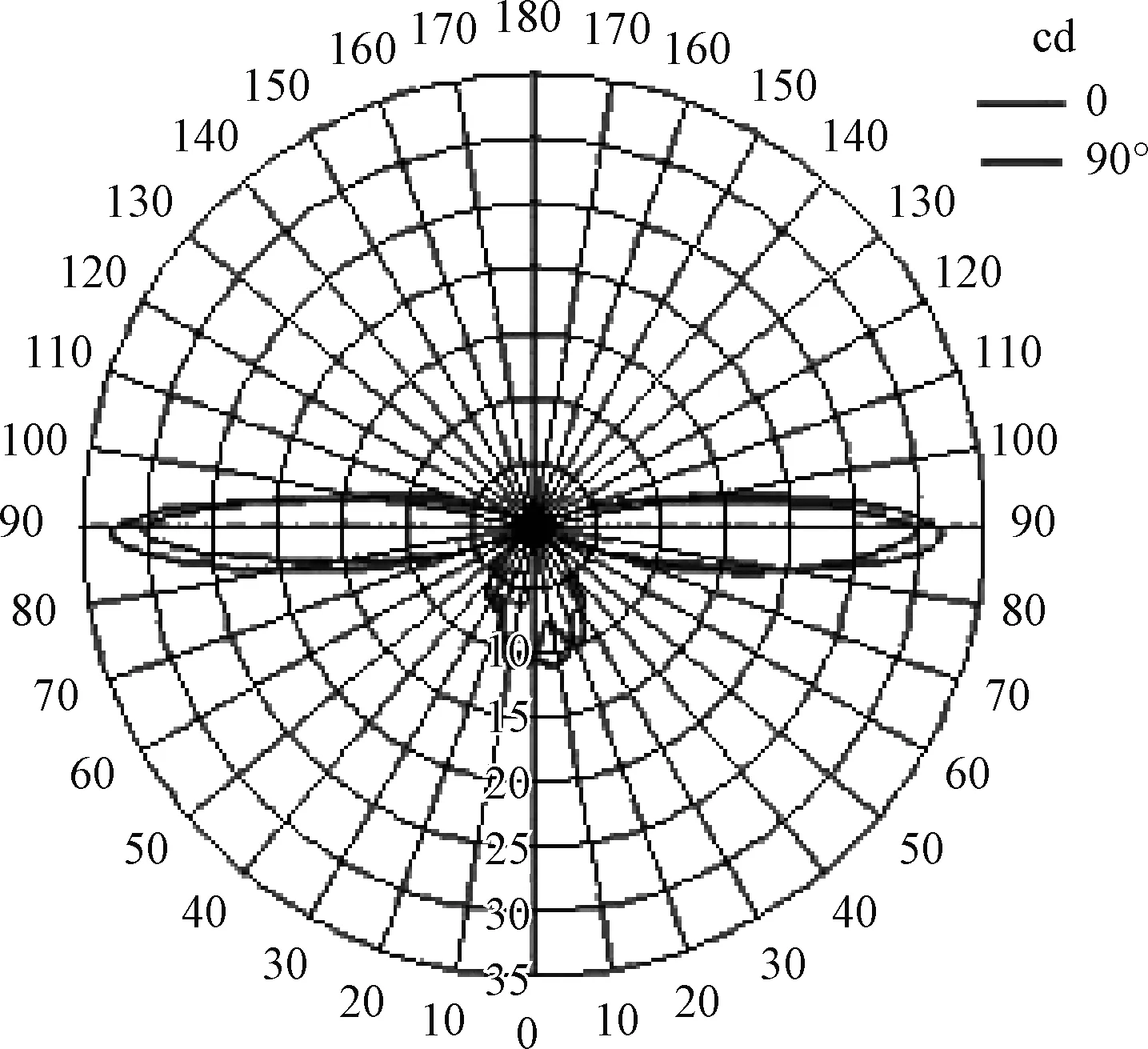
图15 全景透镜的光强分布

以上都是旋转对称透镜，这种2维的计算实际上还可以通过选择不同的照度分布，选择各面是否为直线，选择各面的起始点的位置等来得到多种形状的透镜，在此不一一列举。

3.4 非旋转对称透镜

本方法也可以处理非旋转对称的透镜。此时，要给定各个横截面上不同的照度分布，用3维坐标系计算。图16给出一个18个截面N=20时计算结果的图形，这是一个椭圆形照度分布的TIR透镜，但由于非子午光线的影响，情况会复杂得多，这里不再详细描述。

图16 椭圆照明光斑时的非旋转对称TIR透镜

4 结论

通过给定各面入射线和出射线角度序列和起始点的位置可以求得透镜的表面，其形状和大小都易于控制。计算过程简单，不需要如求解偏微分方程等复杂的方法。而且每一步骤的物理意义和和几何表示都很明确。在计算透射区时，通过设置两个表面的偏折能力权重，可以同步计算和控制两个表面的形状。本方法适用范围很广，可以计算平面表面、自由曲面表面、非准直透镜、事先给定的照度分布和非旋转对称透镜等类型的透镜。