基于生成对抗网络的车辆换道轨迹预测模型

温惠英 张伟罡 赵胜

(华南理工大学 土木与交通学院，广东 广州 510640)

随着自动驾驶技术与车联网技术不断发展与成熟，车辆可以通过传感器与车联网技术定位自身位置与识别周围环境，进而实现对车辆的运动的预测与行为决策。在此背景下，轨迹预测技术可以提升车辆对危险的判断能力与决策能力，通过预测轨迹分析本车与周围车辆预测时段内的运动状态与位置，并对可能的碰撞风险进行判断与分析，从而提升车辆运行过程中的安全性与舒适度。换道行为作为道路交通最基本的交通行为之一，相比车辆的直线行驶，换道车辆需要考虑目标车道上的前后车辆的位置与速度来判断实现换道行为的可行性，其换道轨迹的预测更为复杂与多变。而对换道轨迹的预测可以判断预测时段内换道过程中的车辆碰撞风险，提升换道过程中的安全程度，并辅助车辆的换道决策。

在车辆轨迹预测的研究方面，目前的研究方法主要集中在：基于轨迹模型的预测、概率模型与神经网络模型等。在基于轨迹模型的预测研究中，部分学者通过分析车辆运动学模型，采用动态模型建立轨迹模型[1-2]，但实际拟合效果欠佳。Nelson等[3-4]采用多项式对车辆进行换道轨迹模拟，裴玉龙等[5-6]通过建立车辆的运行轨迹的模型对车辆轨迹进行预测。王世明等[7]根据车辆运动学建立了关于换道车辆运动模型，详细分析了车辆换道轨迹。但上述模型需要参数与约束条件较多，与实际车辆运行轨迹仍有较大差异。

近年来随着新技术的发展，概率模型与神经网络技术也越来越多应用于轨迹预测中：Tomar等[8]提出了一种基于MLP的预测算法，实验结果表明该网络只能对轨迹的离散部分预测，不能实现对全序列的轨迹预测。Altché等[9]通过建立长短时神经网络(LSTM)来预测车辆的横向位移和纵向速度，其结果表明该网络在横向位移与纵向速度的预测上的精度较以往提高，但存在一定延迟，平均误差较高。Kim等[10]则使用LSTM网络结构在栅格图上生成周围车辆的占用概率，结果表明该方法比卡尔曼滤波有着更好的预测精度。Park等[11]采用了基于LSTM的编码器-解码器模型，并通过集束搜索法在栅格图上产生K个最可能的预测轨迹序列，迭代找寻车辆未来最大可能性的轨迹。Gupta等[12]在基于LSTM的编码-解码器的结构上采用生成对抗神经网络(GAN)加强了预测的精度，并生成了未来的行人轨迹，取得了明显的效果。

轨迹预测研究中部分是通过建立轨迹模型来拟合实际车辆轨迹，但该类模型中设置较多的约束条件与参数，且拟合效果欠佳，实际应用中限制较大。采用传统神经网络和概率模型，如MLP和LSTM网络进行轨迹预测，其预测精度相较传统方法有着明显提高，但由于网络结构的限制无法对未来较长的轨迹进行序列预测，而单一时刻的预测位置对于轨迹预测及其后续的决策与判断意义不大。以循环神经网络为代表的轨迹预测模型，相较于传统模型在轨迹序列预测上取得了一定的提升，但由于采用可栅格网占用概率预测车辆坐标，其对轨迹序列的预测实时性与精确度有待提高。

为解决换道轨迹序列预测问题和提升轨迹序列预测的精度，文中通过设计实车换道试验以获取原始换道数据集，通过预处理进一步提取换道轨迹信息。在此基础上，建立基于生成对抗网络的轨迹生成对抗模型，其中轨迹生成网络采用基于LSTM的编码器-解码器结构以处理轨迹序列，根据输入的历史轨迹生成预测轨迹。轨迹判别网络通过多层MLP网络计算预测轨迹与目标轨迹的对抗损失函数，并在对抗损失的基础上，构造关于预测轨迹与目标轨迹的速度损失函数与几何损失函数，通过多重损失函数对网络进行训练，从而实现对本车的预测时段的换道轨迹进行预测。该轨迹生成对抗模型通过交叉验证方法对生成的预测轨迹精确性与有效性进行验证，同时文中分析了不同长度的历史轨迹与预测轨迹对预测精度的影响，并与现有预测模型进行了模型对比，验证了模型的有效性与精确性。

1 轨迹生成对抗网络模型

1.1 生成对抗网络简介

生成对抗网络[13]是一种生成式的对抗神经网络，该网络是通过对抗学习的方式以学习数据分布的生成式模型。生成对抗网络主要由一个生成器G和一个判别器D组成。在训练过程中，生成器和判别器的互相对抗：生成器接收随机的噪声输入以生成一个伪样本，判别器接收真实样本与伪样本，判别输入样本的真伪并输出对样本真伪的判别结果。整个训练过程是生成器与判别器的动态的极小极大博弈过程，则网络的对抗损失函数为：

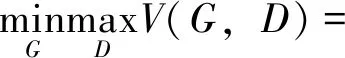
Ex:D[logD(x)]+Ez:G[log(1-D(G(z))]

(1)

式中，x表示输入网络的真实数据，z表示输入网络的噪声，D(x)表示判别器判断输入数据x是否真实的概率，D(G(z))为判别器判断生成器生成的数据G(z)是否真实的概率。在判别器D中，最大化D(x)的对数损失函数使得判别器可以准确地判断输入数据为真实样本或者生成样本，而最大化D(G(z))的对数损失函数使得判别器可以准确判断出伪样本为假，即使得D(x)=1，D(G(z))=0。在生成网络G中，通过最小化D(G(z))的对数损失使得生成样本越接近于真实样本，使得D(G(z))趋近于1。综上所述，使得式(3)最大则判别器的判别能力最强，而使得式(3)最小则生成的样本就越接近真实样本。故整个对抗网络构成了生成器与判别器的极小极大博弈。

1.2轨迹生成模型

文中建立的生成对抗网络如图1所示，生成对抗网络由两部分组成：轨迹生成网络和轨迹判别网络.

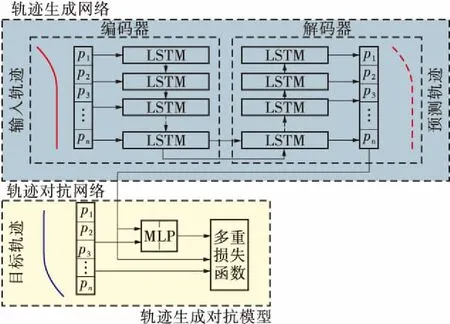
图1 换道轨迹生成对抗网络结构

图1中输入轨迹表示由N个步长的轨迹点组成历史轨迹Lenc，预测轨迹为生成的M步长预测轨迹Lpre，目标轨迹为对应的M步长目标轨迹Ltar。将Lenc输入至编码器中，通过编码器输出上下文向量至解码器中，解码器输出预测轨迹Lpre，并将Lpre传递至判别网络中。在判别网络中计算预测轨迹Lpre与目标轨迹Ltar的多重损失函数。

在处理序列数据上循环神经网络表现出了一定的优越性，而车辆轨迹数据作为与时间相关的序列数据也可采用循环神经网络进行处理，文献[9-12]均采用了相关的网络模型实现对序列数据的预测。故本文轨迹生成网络采用基于LSTM的解码器与编码器结构来实现对未来时段内车辆换道轨迹的生成。该结构是最早由Cho等[14]提出的一种神经网络结构，Sutskever等[15-16]均对该神经网络做出补充与扩展，使得该结构在机器翻译，语音识别等领域内有着出色的表现。其核心思想是通过编码器对输入序列进行编码，将其历史输入编码为一个上下文向量，解码器从上下文向量中提取信息，生成预测的的序列数据。

对一条完整的换道轨迹Li(p1，p2，…，pn)，pt为换道轨迹上t时刻的轨迹点，有：

(2)

式中：xt、yt、vt表示t时刻的轨迹点的平面坐标与速度；Δdt表示t时刻轨迹点与t+1时刻轨迹点间的距离，T为换道轨迹总时长。划分换道全轨迹Li为历史轨迹Lenc、目标轨迹Ltar、预测轨迹Lpre，如图2所示。设Lenc轨迹历史时长为Δenc，轨迹点个数为N，Ltar与Lpre轨迹预测时长为Δpre，轨迹点个数为M。

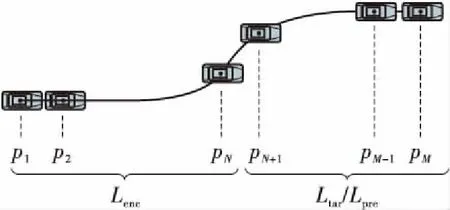
图2 轨迹划分图

编码器中输入历史轨迹Lenc，编码器与解码器的步长设置和历史与预测轨迹点个数相同。编码器在每一个步长的LSTM单元中输入对应步长的历史轨迹点信息pt，并将LSTM单元输出的隐层状态ht在每个步长的循环层单元中传递，最终将历史轨迹信息编码为固定长度的上下文向量c。编码器得到上下文向量的方法有多种[14-16]，文中选择将编码器中最后一个隐层状态hN直接赋值给c得到上下文向量，有：

(3)

式中，pt表示输入编码器的历史轨迹点信息，ht-1表示上一步长的LSTM单元输出的隐层状态，ht表示当前LSTM单元输出的隐层状态，f1为LSTM的输入激活函数，文中采用tanh函数作为LSTM单元的输入层激活函数。w1，wh，b1表示LSTM单元输入层的权重与偏置。c表示在最后一个步长N时输出的上下文向量。

解码器接收上下文向量c，并将c作为解码器的初始隐层状态输入网络。不同于编码器，解码器在网络训练与预测阶段有着不同的策略，如图3所示。

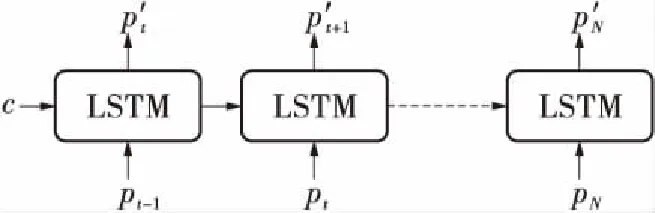
(a)训练阶段

(b)预测阶段

在解码器中，不同于传统的RNN计算方式，即上一个步长单元的输出作为下一个步长单元的输入，文中采用Teacher Forcing[17]作为解码器训练阶段策略：即在训练阶段每次循环单元计算不使用上一个步长的输出作为下一个步长的输入，而是直接使用目标值的对应上一项作为下一个状态的输入。通过Teacher Forcing，可以加快轨迹生成网络的收敛速度，阻断误差积累，提高模型稳定性，增强网络的学习能力。在训练阶段，解码器错位输入预测的目标轨迹序列以训练解码器网络，有：

ht=f1(w1pt-1+whht-1+b1)

(4)

在预测阶段，解码器每个步长接收上一步长循环单元的输出与隐层状态以计算当前步长的隐层状态与输出。有：

(5)

式中，pt′为上一步长LSTM单元的输出值，ht-2表示上一步长单元输入的隐层状态，ht-1表示上一步长单元输出的隐层状态，ht表示当前单元输出的隐层状态。f2为LSTM输出层的激活函数，采用tanh函数作为该层的激活函数，w2、b2为LSTM输出层的权重与偏置，同时解码器中LSTM单元输入层与输出层的权重参数设置与编码器相同。

1.3 轨迹判别网络

轨迹判别网络中，输入预测轨迹与目标轨迹通过分类以判断输入的真假。考虑到轨迹中每个轨迹点所包含的信息(平面坐标、速度等)，故在轨迹判别网络中，为了使得轨迹生成网络生成更为真实可靠的预测轨迹，采用多重判别方式综合判断生成轨迹与真实轨迹的相近程度：通过多层MLP提取轨迹特征并输出轨迹真假概率，计算对抗损失值。同时在对抗损失之外，考虑到生成的预测轨迹与真实轨迹之间的轨迹几何损失与速度损失，综合上述三种损失通过加权组合为多重损失函数。

在判别网络中，输入待判别的J条轨迹数据，J为输入轨迹总个数。设目标轨迹的标签为1，预测轨迹的标签为0，将生成的预测轨迹与目标轨迹交替输入至MLP层中，经MLP层将多维输入一维化，然后对轨迹进行分类，输出轨迹的真假概率，有：

(6)

(7)

相应的，轨迹生成网络的对抗损失函数为：

(8)

文中采取了3种方式对预测轨迹与目标轨迹之间的几何损失进行判断，如图4所示。

图4 几何损失示意图

(9)

(10)

对于轨迹上相邻时刻的坐标点之间的距离Δdt与Δdt′，计算二者间差值作为预测轨迹间隔损失函数L3，有：

(11)

综上所述，轨迹Ltar与轨迹Lpre的几何损失函数Lgeo为：

Lgeo=L1+L2+L3

(12)

考虑每个轨迹点上车辆速度，计算预测轨迹与目标轨迹间的速度差值为对应时刻轨迹点间速度损失Lvel，有：

(13)

故而将对抗损失、几何损失、速度损失这三者加权后线性组合为多重损失函数，轨迹判别网络与生成网络的多重损失函数定义如下：

(14)

式中：LD为判别网络损失；LG为生成网络损失；λ1、λ2、λ3为损失函数权重。在模型的一次训练迭代中，轨迹生成网络G根据输入历史轨迹生成预测轨迹，轨迹判别网络D为最小化目标轨迹与预测轨迹的多重损失函数LD，重复进行k次训练，更新网络权重并在第k次训练后固定判别网络中权重参数。轨迹生成网络在该判别网络权重下生成新的预测轨迹并计算LG，使得LG不断降低，则生成轨迹的判别概率越逼近1，即预测轨迹越接近真实轨迹。通过多次迭代，使得总损失函数不断降低至最优，轨迹生成网络即可生成符合实际车辆换道的预测轨迹。而在预测阶段，可通过已经训练成熟的网络结构生成预测轨迹，即可实现对车辆换道轨迹的预测。

2 实验数据与数据预处理

2.1 实验数据收集

本次实验数据采集选取广州市大学城中环路为实验数据采集路段(见图5)。

图5 换道实验路线图

测试车辆装备高精度GPS仪器(司南导航M 300 TD、M600)对车辆换道轨迹进行高精度的数据采集，该设备由基准站与移动站构成以进行高精度双机共视授时采集坐标，可在环境条件良好，道路上方无严重遮挡的情况下收集车辆移动坐标数据.该系统的采集频率为10 Hz，双机授时精度为±1.67 ns，定位精度可达10 cm，通过基准站对移动站的坐标修正可以精确收集换道轨迹信息.其系统输出包括采集时间、车辆经纬度坐标、经高斯投影计算出的平面坐标和车辆速度等运动数据。设计实验如下：选择10名驾龄大于3年的熟练驾驶员为实验人员，按道路限速要求在实验路段上自由驾驶，要求司机在道路上自由驾驶至可换道区域后视安全情况进行自由换道。实验共收集962组换道轨迹数据，提取输出的平面坐标。

2.2 数据预处理

为便于后续实验处理与模型计算，对原始采集数据通过以下步骤进行数据预处理：

1)数据筛选

为保证选取的轨迹数据可以覆盖车辆换道全过程，选择本车车辆横向速度大于0.2 m/s[18]的时刻视为换道开始时刻t0。考虑换道全过程的平均持续时间为4～5 s[19]，故选取采集数据中时间段为[t0-1 s，t0+3 s]的轨迹数据作为轨迹换道数据，并将t0-1s时刻的轨迹点设为换道轨迹数据的起点。

2)轨迹平移

由于实验仪器提供的轨迹信息是以GPS与基站默认设置的坐标系与大地坐标系为参考坐标系，不便于轨迹数据的处理与后续计算，为便于处理故而需要将轨迹数据转换到以本车为参考的相对坐标系中，则对于轨迹Li={(x1，y1)，(x2，y2)，…，(xn，yn)}，设轨迹中(x1，y1)坐标点为坐标原点，则对每个轨迹坐标点有：

(15)

3)轨迹间隔计算

通过计算轨迹点(xt，yt)与后一时刻轨迹点(xt+1，yt+1)间的欧式距离得到该时刻轨迹点间隔Δdt，有：

(16)

通过数据预处理从原始采集的轨迹数据提取出可用的换道轨迹数据，建立训练数据集，同时在保留轨迹特征的前提下简化了轨迹数据，提取轨迹生成对抗模型所需的车辆换道轨迹属性，提升计算效率。

3 模型配置与计算

文中模型在CPU配置为 Inter Core i7-5 500 U 2.40 GHz的笔记本上运行相关代码，轨迹生成对抗模型代码采用Python 3.0 和 TensorFlow 1.12为环境编写完成。其中，轨迹生成网络中，LSTM单元隐层维度设为12，编码器与解码器的参数设置相同。轨迹判别网络中，设置MLP层为两层且判别器每次迭代单独训练次数k=1。参数优化器选择RMSProp优化器，设定其初始学习率为0.007，学习衰减率为0.9，动量参数为0.5，总损失函数权重设为λ1=0.4、λ2=0.3、λ3=0.3。

从采集的数据中，经预处理提取数据集包括700条车辆换道轨迹。取历史轨迹时长Δenc=2 s，轨迹点个数N=20；预测/目标时长Δenc=Δtar=2 s，轨迹点个数M=20。取数据集中前80%组成训练集，后20%组成测试集，通过交叉验证来评估生成轨迹效果。总训练次数设为1 000次，经过网络计算输出训练误差与预测坐标。为便于直观的了解训练误差的波动情况，将输出的训练误差转换到log范围，如图6所示。

图6 训练误差图

从图6可知，在训练次数为1 000次的条件下，全训练过程中网络误差呈波动下降趋势，训练次数达400次左右时，误差逐渐减缓且仅在小范围内上下波动，此时模型趋于稳定直至达到最大训练次数。从测试集中随机抽取部分输出的预测轨迹与目标轨迹对比，并计算对应时刻的轨迹点间欧式距离，如图7所示。

(a)Δenc=2 s，Δpre=2 s，轨迹1

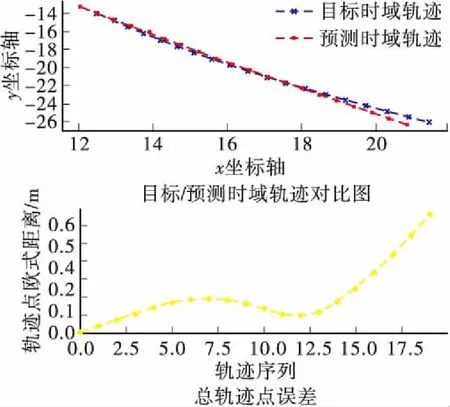
(b)Δenc=2 s，Δpre=2 s，轨迹2

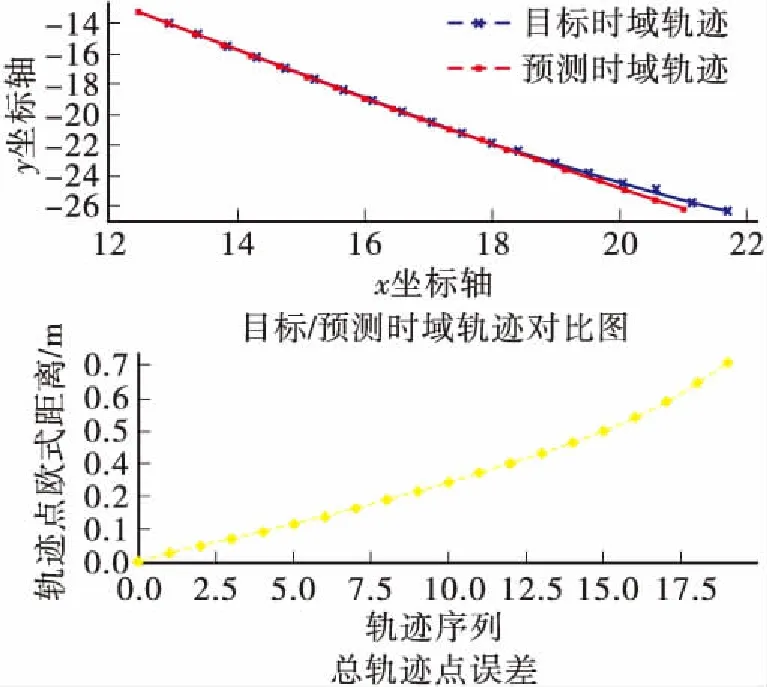
(c)Δenc=2 s，Δpre=2 s，轨迹3

(d)Δenc=2 s，Δpre=2 s，轨迹4

结合图7可知，在历史轨迹时长Δenc=2 s，预测轨迹时长Δpre=2 s的条件下，预测轨迹上的平面坐标点与换道目标轨迹坐标点基本相接近，且距离起始点越近的轨迹坐标点预测越精确，较远的轨迹坐标点的误差有所增加。表1对比了不同历史轨迹时长与预测轨迹时长的取值对预测结果的影响。在相同的历史轨迹时长下，随着预测时长的增加，预测序列的坐标点误差也随着增加：在Δenc=1 s，Δpre=1 s时轨迹坐标点平均总误差为0.35 m，平均x坐标与平均y坐标误差分为0.27 m和0.18 m。而在Δenc=1 s，Δpre=2 s时，轨迹坐标点平均总误差为0.47 m，平均x坐标与平均y坐标误差分别为0.34 m和0.26 m。相比Δpre=2 s，Δpre=1 s时的轨迹点误差降低了25%，x坐标与y坐标误差降低了21%与31%。分析该误差的产生是由于预测轨迹序列的增长导致网络中的误差不断累积，使得较远的轨迹坐标点距离实际目标轨迹偏差增加。在相同预测时长下，历史轨迹时长越长，其轨迹误差越低：如Δenc=1 s，Δpre=1 s与Δenc=2 s，Δpre=1 s时，轨迹坐标点误差分别为0.35 m与0.28 m，后者相较前者误差降低了20%。该误差的降低说明在相同预测轨迹时长条件下，长度越长的历史轨迹，其预测轨迹的精度越高。

表1 不同预测长度的轨迹误差均值

表2对比了在同一预测长度下不同预测模型与参数选择对换道轨迹的预测效果，包括平均x坐标、y坐标误差与轨迹的平均总误差。文中，对比模型选择了MLP神经网络、单一LSTM模型和基于LSTM的编码-解码器结构，同时对比了不同损失函数对轨迹生成对抗模型精度的影响。

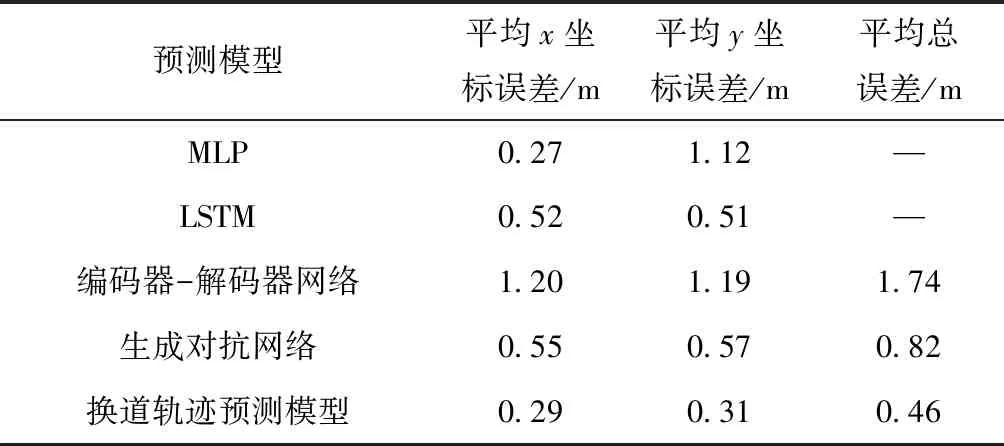
表2 预测模型对比(Δenc=2 s，Δpre=2 s)

对比结果显示，单一结构的神经网络模型，如MLP、LSTM仅可以实现对单点轨迹坐标进行预测，而由于其网络结构限制无法一次性预测长序列的轨迹坐标。故MLP与LSTM模型仅存在平均单个轨迹点的坐标误差，不存在平均总误差。而在轨迹序列预测中，相比单一的编码器与解码器结构，轨迹生成对抗网络在单个轨迹坐标点的预测和整体轨迹的预测上的精度有着一定的提升。同时在轨迹生成对抗网络中，通过引入速度损失与几何损失的多重损失可以进一步的提升预测精度，降低误差：采用多重损失使得平均x/y坐标误差降低了47%与45%，总轨迹点误差降低了44%。由表2可知，通过添加多重损失函数可显著降低模型误差，提升预测轨迹的精确度。

综上所述，通过交叉验证与模型对比可知，文中提出的轨迹生成对抗模型可以在不同预测长度下，对预测时段内的换道轨迹进行较为精确的预测，经生成网络预测出的换道轨迹可以基本满足实际应用要求。相较于传统轨迹预测模型，轨迹生成对抗模型解决了无法一次预测长序列轨迹的问题，同时也通过多重损失函数大大降低了模型误差，提升了预测精度。

4 结语

(1)文中提出了一种基于生成对抗网络的车辆换道轨迹生成对抗模型，实现了对车辆未来换道轨迹的序列预测。该轨迹生成对抗模型由基于编码器-解码器结构的轨迹生成网络与基于MLP的判别网络组成，由轨迹生成网络根据输入的历史轨迹生成预测轨迹，并通过轨迹判别网络对该预测轨迹进行多重判别。经训练，该模型表现出了较好的预测效果，较原有轨迹预测模型的精确度有了明显提升。

(2)文中对比了不同预测时长对预测结果的影响，结果显示轨迹误差随着预测长度的增加而增加，较短的预测时长有着更高的精确度。通过对比不同预测模型的预测效果，验证了该轨迹生成对抗网络在长序列换道轨迹的预测上有着更好的精确度。故而通过该模型，在实际的车辆运行中可以通过动态的选取预测长度，根据需求与计算能力实时地对换道轨迹进行预测，生成较精确的预测轨迹。同时可在车联网环境与自动驾驶技术支持下通过传感器实时地与周围运行车辆交互，从而获取周围车辆运行动态，并可根据该模型输出的预测轨迹判断未来换道过程中的车辆碰撞风险，为车辆提供辅助换道决策依据，提升换道安全。

(3)本模型是基于换道场景下的换道轨迹预测研究，在其他车辆运行场景(如直线行驶，转弯，超车等)中的应用有待研究，研究不同运行场景下的轨迹预测模型与优化预测网络结构，提升轨迹预测精度将是下一步研究的方向与重点。