基于数值子结构的OpenSees与LS-DYNA联合计算

张宁 张德宇 古泉

(厦门大学 土木工程系， 福建 厦门 361005)

土木工程领域的研究多种多样，包括抗震、抗冲击、防火、防爆等。众多的数值模拟软件也各有其优势，且在各自适用的领域发挥其作用。现如今，学者们往往会选择最合适的软件进行所选问题的分析。例如，对于框架结构抗震的分析采用OpenSees[1]，对于精细模型抗冲击问题的模拟采用LS-DYNA[2]。但是当研究混合类型的问题时，单一的软件就较为吃力。例如，对于冲击作用对框架结构的影响问题，不仅需要对直接受冲击单元进行模拟分析，也需要对受冲击作用之后结构的后续变形进行研究。且在这种情况下，直接受冲击单元进入强非线性状态，而整体结构往往仍处于线弹性阶段。单独使用OpenSees难以模拟冲击问题，若采用LS-DYNA对结构进行精细化非线性模拟，不仅建模繁琐，接触判断复杂，而且计算耗时严重。

ECC材料因其特有的高延性抗拉性能和耗能能力，逐渐被应用于框架结构之中[3-7]。文中首次提出基于NSM的OpenSees与LS-DYNA联合计算，以研究ECC材料对于结构抗冲击方面的作用[8-10]。其主结构采用OpenSees进行线弹性分析，子结构采用LS-DYNA进行非线性分析。通过算例和分析，验证了OpenSees与LS-DYNA联合计算的可行性和正确性。

1 数值子结构方法

1.1 基本原理

数值子结构方法的思想是通过将整体结构的非线性分析分解为主结构和子结构两个部分，从而实现简化计算。其中，对于主结构采用线弹性分析，对于子结构采用非线性分析。从网格划分上来看，主结构采用较为粗糙的网格，而子结构因其涉及到非线性分析，故采用更为精细化的网格。两部分依据边界力和变形协调条件完成联合计算[11-12]。数值子结构方法的推导是在运动方程的基础上采用Newmark-β法进行离散。运动方程为

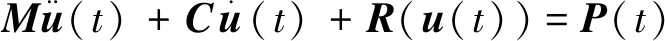
(1)

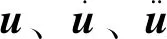
(2)

式中，

(3)

n表示上一荷载步，α和β分别为Newmark-β法中的控制参数(α=0.5，β=0.25)；Δt为时间步长。在式(2)左右加上Kun+1，K为结构初始刚度矩阵，可推导出：

Fn+1+[Kun+1-R(un+1)]

(4)

定义等效动力刚度，即：

(5)

定义非线性修正力为

(6)

由以上推导出整理后的平衡方程：

(7)

1.2 OpenSees与LS-DYNA联合计算

OpenSees和LS-DYNA各有其最佳适用的分析领域。结合两者的优势，文中提出由OpenSees负责主结构线弹性部分的计算，由LS-DYNA负责子结构进行精细化部分的计算。采用Matlab工具作为总控制端，分别调用OpenSees和LS-DYNA以实现两个平台基于数值子结构方法的联合计算。具体计算分为以下几步。如图1所示。

图1 OpenSees与LS-DYNA联合计算流程图

Fig.1 OpenSees and LS-DYNA combined calculations flow chart

第1步使用Matlab导入java.awt.Robot和java. awt.event.*类，实现Opensees和LS-DYNA之间的数据的读取和部分操作。

第2步Matlab运行OpenSees平台进行当前时步主结构的线弹性分析。OpenSees的分析一般采用source功能读取Tcl文件的方式以执行已写好的外部命令文件。OpenSees采用了Tcl语言作为用户交互接口，用户可以在Tcl文件中设置接口以进行数据的记录和传递。为了实现基于NSM的联合计算，在Tcl文件中设置了单元边界位移un和线弹性力Kun的数据传递接口，并将其数据保存到out文件中，以方便Matlab的读取和随后的传递。

第3步Matlab运行LS-DYNA平台进行当前时步子结构的非线性分析。相比于开源软件Open-Sees，LS-DYNA的运行采用读取事先写好的k文件进行分析。OpenSees可以在每一时步进行数据的读取和修改以满足下一时步计算的需要。而LS-DYNA不具有这种能力，故需要采用重启动功能。根据数值子结构的思路，运用小型重启动功能，设置每个时步为中断点，通过修改随后的求解时间和调整边界位移un来进行下一步的分析。LS-DYNA在进行小型重启动的过程中，需要读取上一次计算的结果(D3DUMP文件)，以及修改后的k文件以完成下一时步的计算。

根据数值子结构方法，子结构的计算需要通过Matlab读取OpenSees记录的out文件，并将其中的边界位移un通过修改k文件的方式传递给LS-DYNA。从LS-DYNA的关键字来说，用户需要通过修改*CONTROL_TERMINATION来控制求解时间；修改*BOUNDARY_PRESCRIBED_MOTION_NODE来控制下一时步的边界条件，包括节点处的位移和转角以及各自的速度和加速度。需要注意的是，一般荷载和边界条件的设定需要定义*DEFINE_CURVE关键字来实现。而*DEFINE_CURVE关键字中时间的长度不能通过小型重启动进行修改，但是数值可以修改，故需要预先设定足够长的时间，通过修改*DEFINE_CURVE中每一时步的数值实现重启动。

LS-DYNA不能通过设置接口的方式将非线性力Rn的计算结果传递给OpenSees，文中采用将非线性力Rn的计算结果通过*DATABASE_NODFOR和*DATABASE_ELOUT两个关键字记录到nodfor和elout两个文件之中。而Matlab通过读取nodfor和elout两个文件获得非线性力Rn。

4)计算非线性修正力Pn。

非线性修正力Pn的计算可以通过Matlab直接计算，将计算后的非线性修正力叠加到主结构之中，并进行下一时步的计算。在以后每一时步的计算之中均重复，如图1所示。

2 数值子结构算例

通过两个算例验证并分析基于数值子结构的OpenSees和LS-DYNA联合计算的可行性和正确性。

2.1 算例1：简支梁受均布荷载

以简支梁受均布荷载为例，如图2所示。其中，向下的均布力大小为q=1 kN/m，梁的跨度L=1 m，截面宽度B=0.5 m，高度H=0.5 m。弹性材料强度为E=2×105kPa，μ=0.2。跨中挠度的解析解为，

(7)

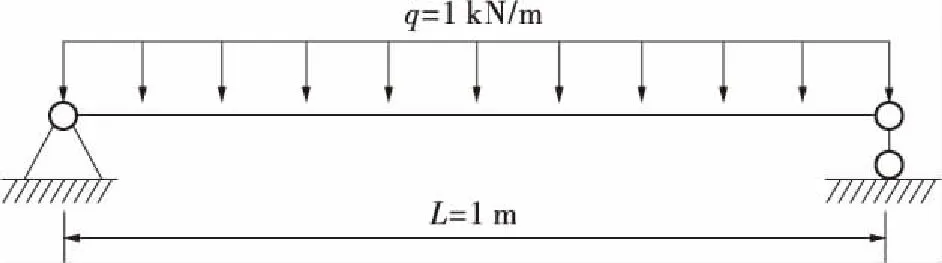
图2 简支梁受均布荷载

文中将OpenSees模拟、LS-DYNA模拟以及两平台联合计算结果与解析解结果进行对比。如图3所示，OpenSees的建模采用了dispBeamColumn单元，材料采用了Steel01材料，并将1 m长的简支梁划分为10个单元。使用eleLoad和beamUniform命令进行均布加载，加载过程分为10步进行，每次加载大小为0.1 kN/m。LS-DYNA的模拟加载过程与OpenSees相同，利用*DATABASE_NODOUT命令记录跨中节点挠度。网格划分与OpenSees相同，其余建模部分不再赘述。

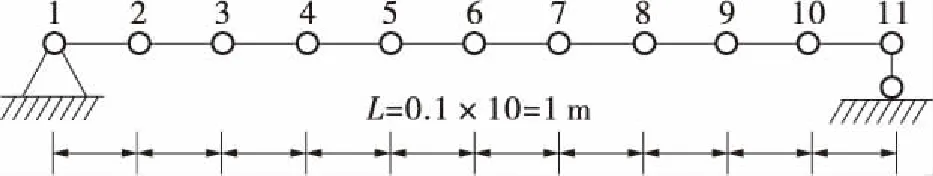
图3 简支梁有限元模型

基于NSM的两平台联合计算将图3分为如图4所示的两个部分。在OpenSees进行主结构计算的基础上，根据数值子结构的原理，将节点5和7的边界位移条件un取出，传递到网格更为精细的LS-DYNA模型中。利用Matlab，将LS-DYNA计算出的非线性力Rn传递到主结构OpenSees之中，计算非线性修正力Pn，具体实现方式如前所述。

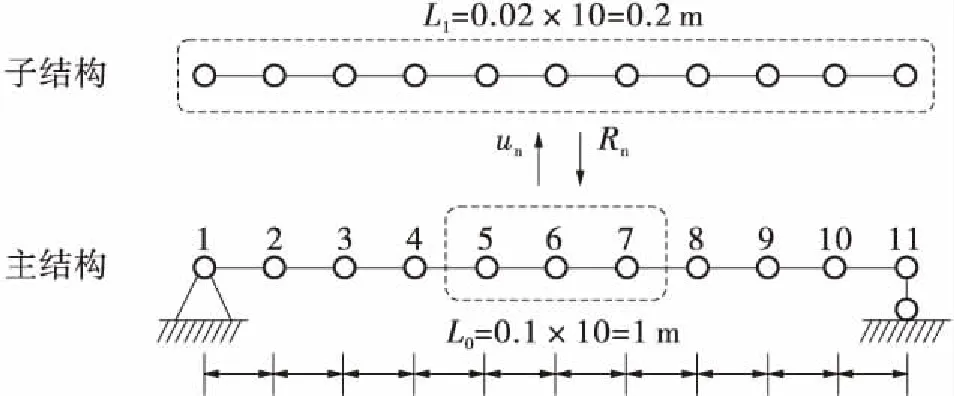
图4 基于NSM的联合计算示意图

将OpenSees模拟、LS-DYNA模拟以及两平台联合计算的结果与解析解进行对比并整理，结果如表1所示。

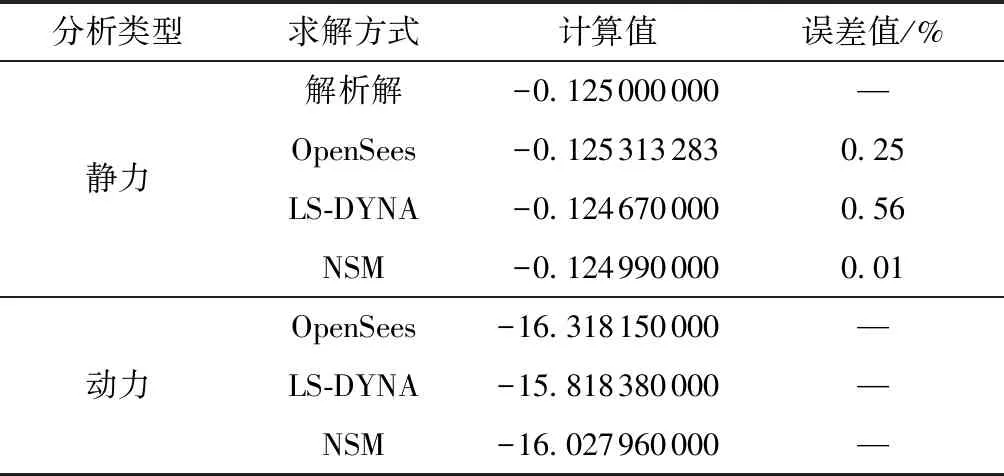
表1 计算结果与分析

从表1的结果上看，OpenSees和NSM的计算结果基本同解析解一致，且NSM由于使用了更为精细的网格，计算结果更好。且NSM原理的设计最初是为了解决混合类型的问题，通过联合OpenSees和LS-DYNA平台，最大化发挥两种软件在各自领域的作用，使解决单一软件无法模拟的混合问题成为可能。从该角度分析，文中设计和开发的基于数值子结构方法的OpenSees与LS-DYNA联合计算模型可以较好的满足这一要求。

2.2 算例2：框架结构在冲击作用下响应分析

LS-DYNA最初是用来分析较为真实的物体碰撞冲击等问题。但如果采用整体精细化建模，工程量和计算量巨大，接触关系的判断也消耗大量时间。前述提到的数值子结构方法可以较好地应对这类问题。本算例通过模拟框架结构在冲击作用下的响应来说明数值子结构方法的可行性和正确性。该框架结构采用纤维截面建模，且内部材料使用本构关系较为复杂的ECC材料。如图5所示。

图5 框架结构示意图(单位：mm)

框架结构中每层尺寸为6 m×6 m，高度为3×3.6 m，底部固定3个方向的位移和转角。梁柱截面采用纤维截面，尺寸为300 mm×300 mm。柱单元内部采用混凝土和钢筋组合纤维截面，纵向钢筋由八根钢筋(Φ20 mm)提供，相对于轴线对称布置，附40 mm保护层。具体布置方式如图6所示。分别采用ECC材料和混凝土材料进行数值模拟[13]，材料的参数如表2所示。ECC材料单轴拉压本构曲线如图7所示。具体的本构滞回关系和材料参数来源于Han[14]。

楼板采用刚性楼板，梁柱的弹性模量为3.25×104MPa。建立三维模型，计算步长取0.000 1 s。文中设置子弹以1 000 m/s的速度对节点6和节点11中间的柱单元1进行冲击以模拟子弹冲击框架结构。文中假定弹体为刚体，忽略子弹侵彻对结构的影响，仅考虑直接受冲击单元进入强非线性状态的分析，以及冲击后对整体框架的影响。基于NSM的算法，将整体框架定义为主结构，采用较为粗糙的网格划分，使用OpenSees进行数值模拟。利用OpenSees中的uniaxialMaterial Elastic进行材料线弹性阶段的分析，并记录节点6和11的边界位移un(包括3个方向的位移和转动以及各自的速度和加速度)，将其传递给子结构。其余的接口设置、数据传递方式，以及启动与等待点的设置如前例所述[15-19]。

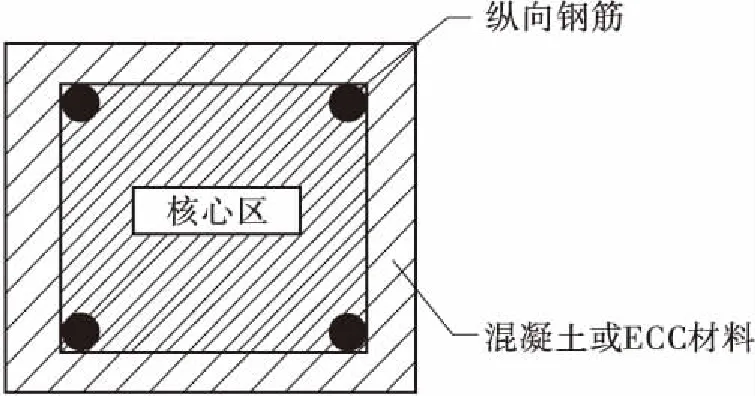
图6 纤维梁柱截面示意图

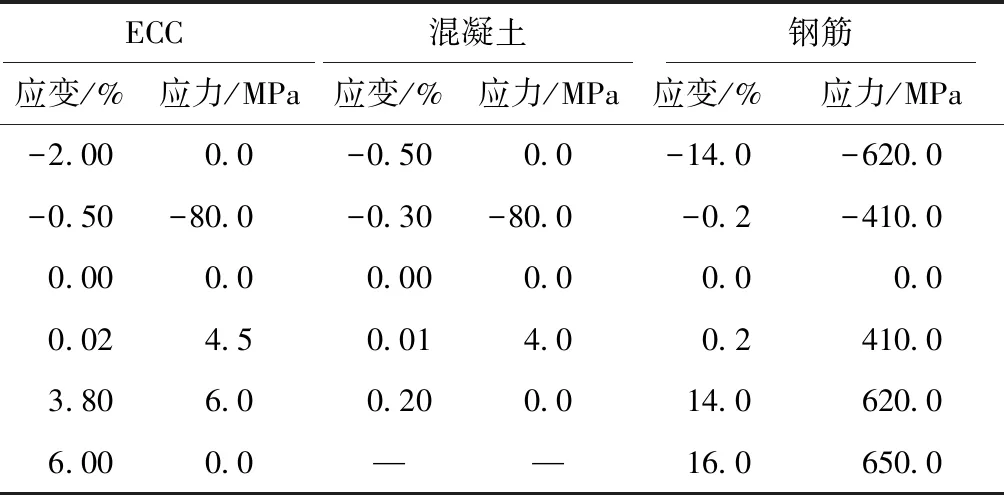
ECC 混凝土 钢筋 应变/%应力/MPa应变/%应力/MPa应变/%应力/MPa-2.000.0-0.500.0-14.0-620.0-0.50-80.0-0.30-80.0-0.2-410.00.000.00.000.00.00.00.024.50.014.00.2410.03.806.00.200.014.0620.06.000.0——16.0650.0

子结构采用LS-DYNA进行建模分析，使用较为精细化的网格。对于子结构的建模分为柱单元1和子弹两部分组成。其中子弹部分的建模，参考了55式37 mm曳光杀伤弹，口径37 mm，弹丸部分长度174 mm，平均密度约8 000 kg/m3，弹丸重0.7 kg，属于较小型的炮弹。本例中假设子弹以1 000 m/s的速度冲击单元1。单元1共分为24个单元，单元的上下两端用*BOUNDARY_PRESCRIBED_MOTION_NODE命令进行位移速度以及加速度的加载和控制。

数值模拟结果分析如图8-图12所示。

由图8和图9可知，在子弹冲击柱单元之后，柱体发生了强烈的变形。随着时间的增加，使用了混凝土材料的柱单元发生了明显大于ECC的变形，且从变形图上看，混凝土柱单元变形严重，且跨中部分明显进入强非线性。由于ECC较好的韧性和较大的抗拉屈服应变，使用ECC材料的柱单元变形曲线较好，且跨中位移较小，较好的抵抗了子弹的冲击。由图10和图11可知，受子弹作用的影响，柱单元中所使用的混凝土材料很快达到了设计的极限抗拉应变并退出工作。而所使用的ECC材料在屈服之后仍可以承担一定的拉力，并正常工作。且使用ECC材料的柱单元，其内部钢筋的应变明显小于混凝土柱单元中钢筋的应变。

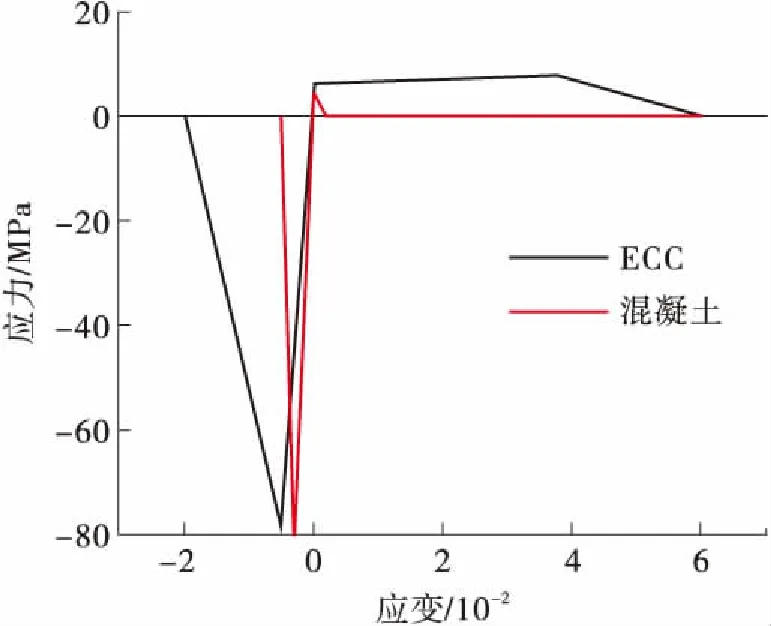
图7 材料单轴拉压示意图

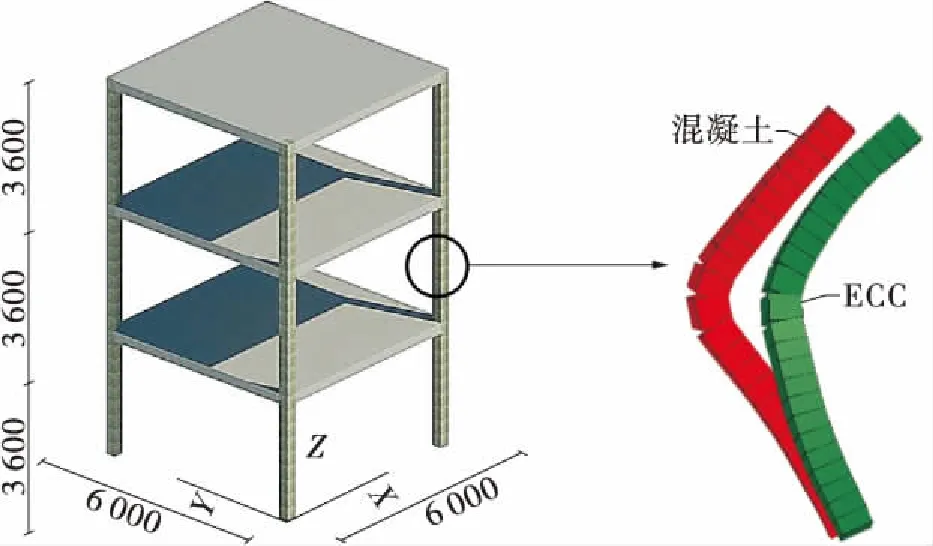
图8 单元1变形示意图

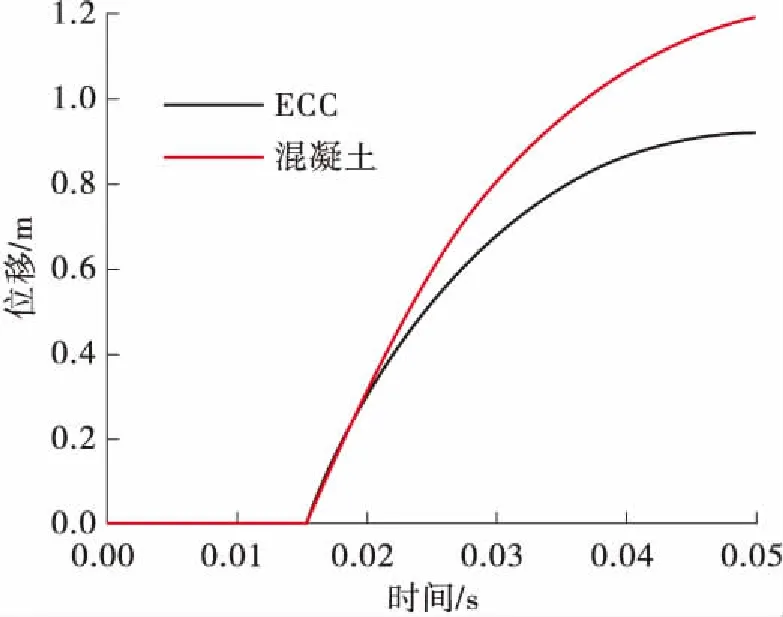
图9 单元1跨中位移示意图

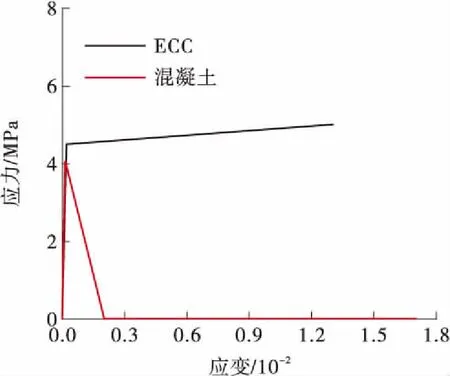
图10 混凝土纤维应力应变曲线

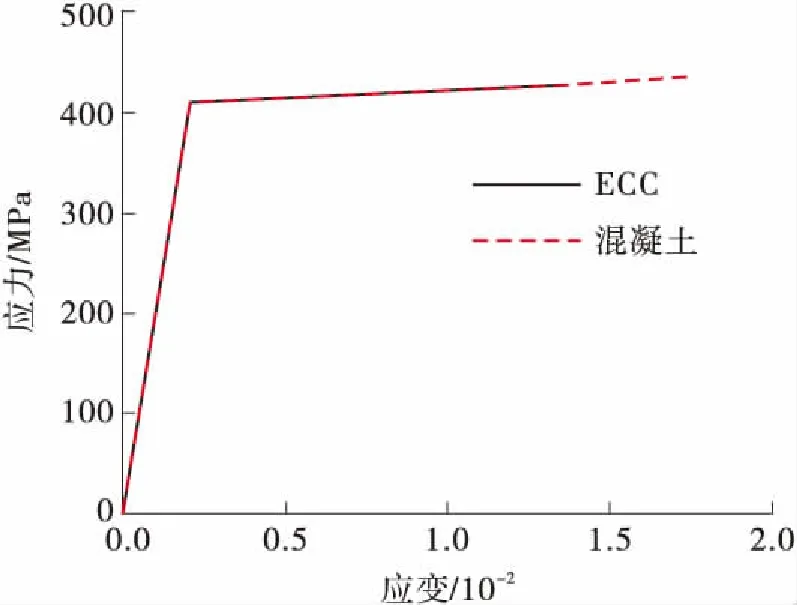
图11 钢筋纤维应力应变曲线

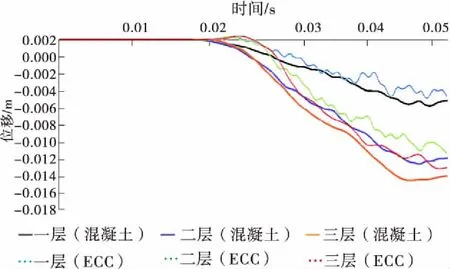
图12 楼板侧向位移示意图

由图12可知，从主结构计算的结果来看，子弹对主结构的冲击有着不可忽视的作用，且在使用ECC材料后，楼板的侧向位移得到了一定的限制，特别是对于更高楼层的位移，限制结果更明显。本算例不仅验证了NSM方法的可行性和适用性，也体现了ECC材料在性能方面一定程度上优于混凝土材料。

3 结论

文中基于数值子结构的理论，提出并实现了OpenSees与LS-DYNA联合计算的方法。采用OpenSees进行大规模主结构的线性分析，用LS-DYNA进行局部精细化隔离子结构的非线性分析。用Matlab做主控制程序，通过分别调用OpenSees和LS-DYNA实现两个软件平台的联合计算。该过程采用位移控制等命令保证了边界位移协调，并通过非线性修正力的计算保证主结构和子结构受力的等效性。利用新建的OpenSees和LS-DYNA联合计算平台对受均布荷载的连续梁进行分析，通过与解析解、单独用OpenSees计算结果和单独用LS-DYNA计算结果对比，验证了所提的基于数值子结构方法的OpenSees和LS-DYNA联合计算方法的正确性和可行性。利用该平台，对一个三层ECC框架结构受子弹冲击的算例进行数值模拟。其结果说明该方法可以用于纤维截面和复杂本构模型的简化计算。基于数值子结构的OpenSees和LS-DYNA联合计算方法为整体结构局部受到强冲击作用的诸类混合问题提供了一个可行且优化的计算方法。