垂直线源灌不同线源直径下的入渗规律及其模型适用性研究

程慧娟，张俊友，王全九

(1.内蒙古农业大学职业技术学院，内蒙古 包头 014109；2.西安理工大学水资源研究所，西安 710048 ；3.中国科学院教育部水土保持与生态环境研究中心 黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西 杨陵 712100)

0 引 言

新疆地处亚欧大陆，干旱少雨，蒸发量大，属于温带大陆性荒漠气候，经济发展主要来源于灌溉农业，水资源短缺成为影响新疆经济社会发展的制约因素[1,2]。因此，发展节水灌溉技术，提高水资源利用效率，是解决水资源短缺的重要途径之一。

常用的滴灌、渗灌等灌溉方式虽然起到了节水的作用，但其滴头易堵塞、灌水均匀度不易控制[3]，因此提出了垂直线源灌。垂直线源灌是一种适合果树等多年生深根植物的节水灌溉方式，其特点为：灌水深度和宽度可通过线源长度和线源直径进行调整，灌水器上个别孔堵塞后不影响灌溉质量，并且便于维修。目前，垂直线源灌方面的研究主要有：曾晨研究了不同初始含水量的入渗特性[4]，李淑芹研究了水分分布的数值模拟[5]，范严伟研究了土壤入渗特性和湿润体特性[6,7]。土壤水分入渗规律对于指导灌溉非常重要，刘婧然等主要研究了滴灌、微润灌、涌泉灌等方式下土壤水分入渗规律[8-10]，上官玉铎等对常用入渗模型的适用性进行了研究[11-15]。而常用入渗模型在垂直线源下的适用性缺少研究，因此，本文通过室内土箱模拟试验，研究了垂直线源灌不同线源直径下的入渗规律，并比较了三种入渗模型的适用性，得出了相应的经验公式，为垂直线源灌技术推广应用提供理论依据。

1 材料与方法

1.1 供试土样

供试土样取自新疆鄯善县，经风干、碾碎、过2 mm筛后，利用马尔文激光分析仪测定其基本物理特性(见表1)。

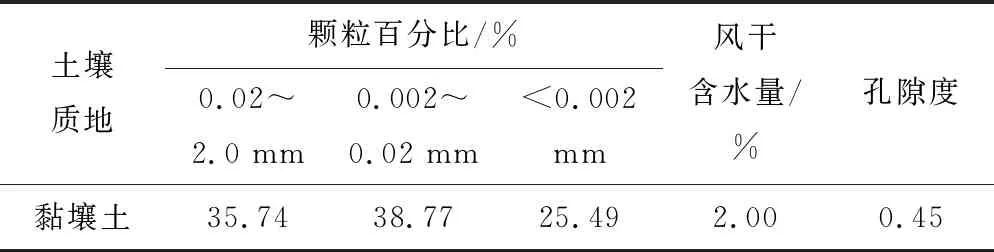
表1 土壤基本物理特性

1.2 试验设备与设计

试验设备主要包括马利奥特瓶(简称马氏瓶)、垂直线源供水管和试验土箱。马氏瓶底面积为500 cm2，高为40 cm；垂直线源供水管进口端连接橡皮管，边壁开孔(开孔率为10%)并用纱布包裹，出口端用堵头密封，管中填充有直径为3～5 mm的碎石，将其垂直插入土体中，第一个出水孔距离土体表面5 cm；试验土箱是长宽高分别为80、60、60 cm的有机玻璃箱，试验设备如图1所示。

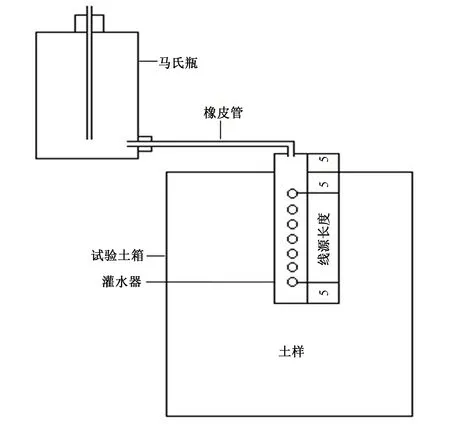
图1 试验设备示意图

本试验主要进行不同线源直径条件下土壤水分入渗特性的研究。试验设置恒定的供水水头为12.5 cm，线源长度为30 cm，线源直径设置了4个水平，分别为2、3、4及5 cm，每组试验3次重复。将供试土样按1.45 g/cm3的容重分层(每层5 cm，层间打毛)装入试验土箱中，安装好马氏瓶和垂直线源供水管，打开阀门，入渗试验开始。试验过程中，记录马氏瓶读数。灌水4 h后，入渗试验结束。用Spss软件和Excel对数据进行分析处理。

1.3 基本理论

模拟土壤水分入渗的常用模型有Green-Ampt入渗模型、Philip入渗模型、Kostiakov(1932)入渗公式和Horton(变形)入渗公式。前两种属于理论入渗模型，后两种属于经验入渗模型[12,16]。Green-Ampt入渗模型是干土积水入渗模型，不适用于垂直线源灌，因此采用其他3种入渗模型进行模拟。

Philip入渗模型采用垂直入渗形式[16]：

i(t)=0.5St-0.5+A

(1)

I(t)=St0.5+At

(2)

式中：i(t)为入渗率，L/h；I(t)为累积入渗量，L；t为入渗历时，h；S为吸渗率，L/h0.5；A为稳渗率，L/h。

Kostiakov(1932)入渗公式为[16]：

i(t)=Bt-α

(3)

(4)

式中：B和α为经验参数。

Horton(1940)入渗公式为[16]：

i(t)=ic+(i0-ic)e-βt

(5)

(6)

式中：ic、i0和β为经验参数。该式可简化为：

i(t)=Ne-wt

(7)

(8)

式中：N和W为经验参数。式(7)和式(8)称为Horton(变形)入渗公式。

2 试验结果与分析

2.1 线源直径对土壤入渗的影响

线源直径改变了垂直线源灌水器的表面积，为了分析对比线源直径对土壤水分入渗的影响，点绘了不同线源直径土壤水分的入渗率和累积入渗量(见图2、3)。

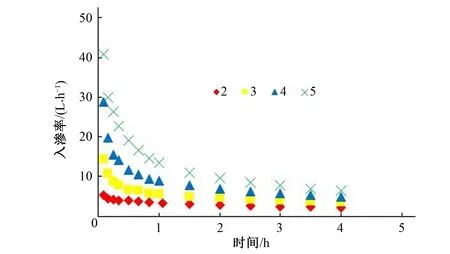
图2 不同线源直径的入渗率

由图2可知，不同线源直径的入渗率变化趋势基本一致，随着入渗历时的延长，入渗率均在降低，且降低幅度逐渐变缓，最终趋于稳定。线源直径对入渗率有明显影响，入渗历时相同时，随着线源直径的增加，入渗率逐渐增大。

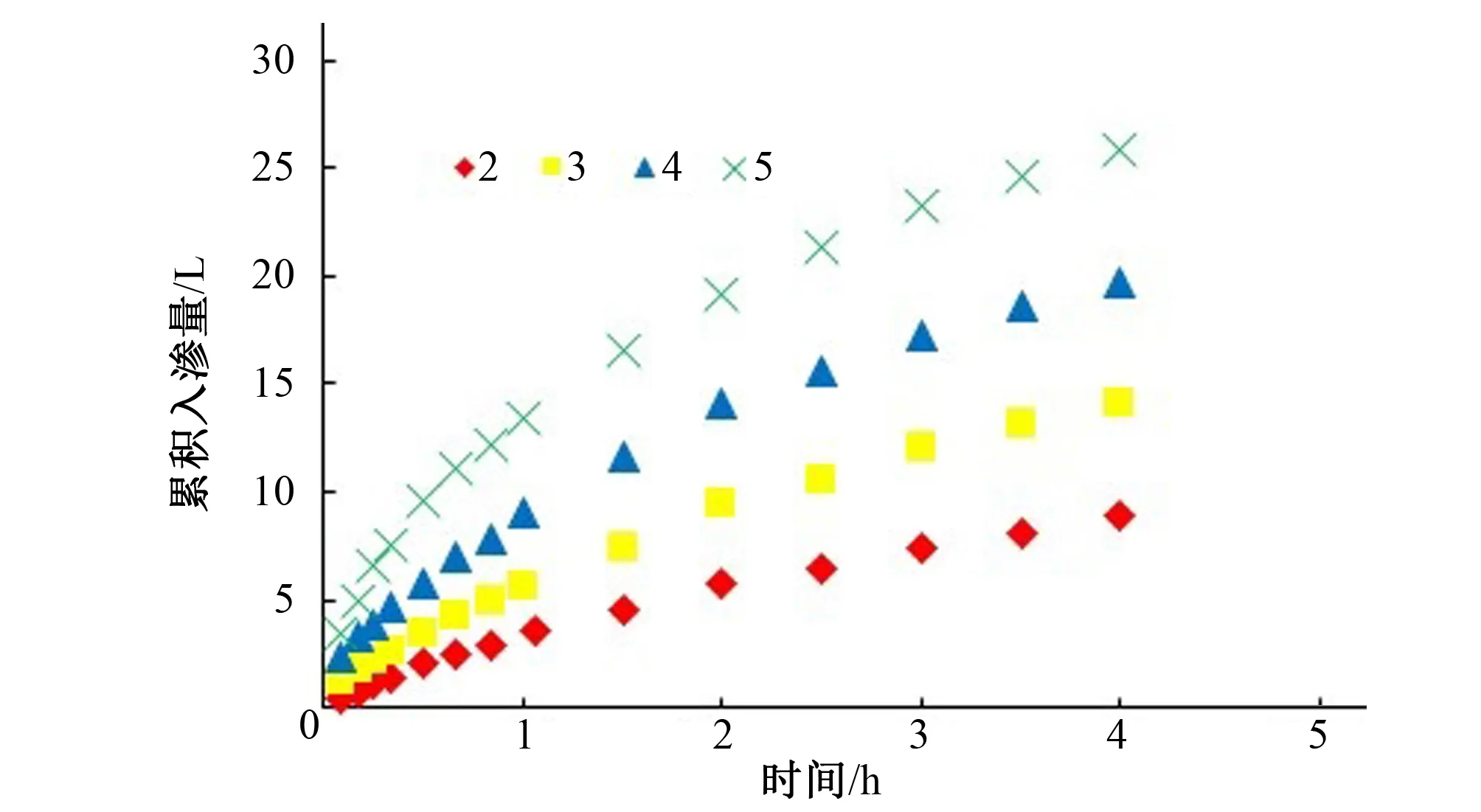
图3 不同线源直径的累积入渗量

由图3可知，不同线源直径的累积入渗量变化趋势基本一致，随着入渗历时的延长，累积入渗量均在增加，且增长幅度逐渐变缓；线源直径对累积入渗量有明显影响，入渗历时相同时，随着线源直径的增加，累积入渗量逐渐增大。

2.2 3种入渗模型对线源直径的适用性

分析了3种入渗模型在不同线源直径条件下土壤水分入渗率的拟合情况，对比了3种入渗模型模拟入渗率和实测入渗率之间的精确性。

2.2.1 Philip入渗模型对线源直径的适用性

将不同线源直径下实测入渗率用Philip入渗模型进行模拟，由模拟结果可知线源直径对穏渗率 影响较小，这是因为不同线源直径的灌水器和土体的接触深度一致。因此，设定不同线源直径的穏渗率A为1.609(平均值)重新进行模拟，模拟结果如图4和表2所示。图4是Philip入渗模型不同线源直径下的入渗率，反映了Philip入渗模型所模拟的入渗率和不同线源直径下实测入渗率的对比关系。表2是Philip入渗模型不同线源直径下的参数。

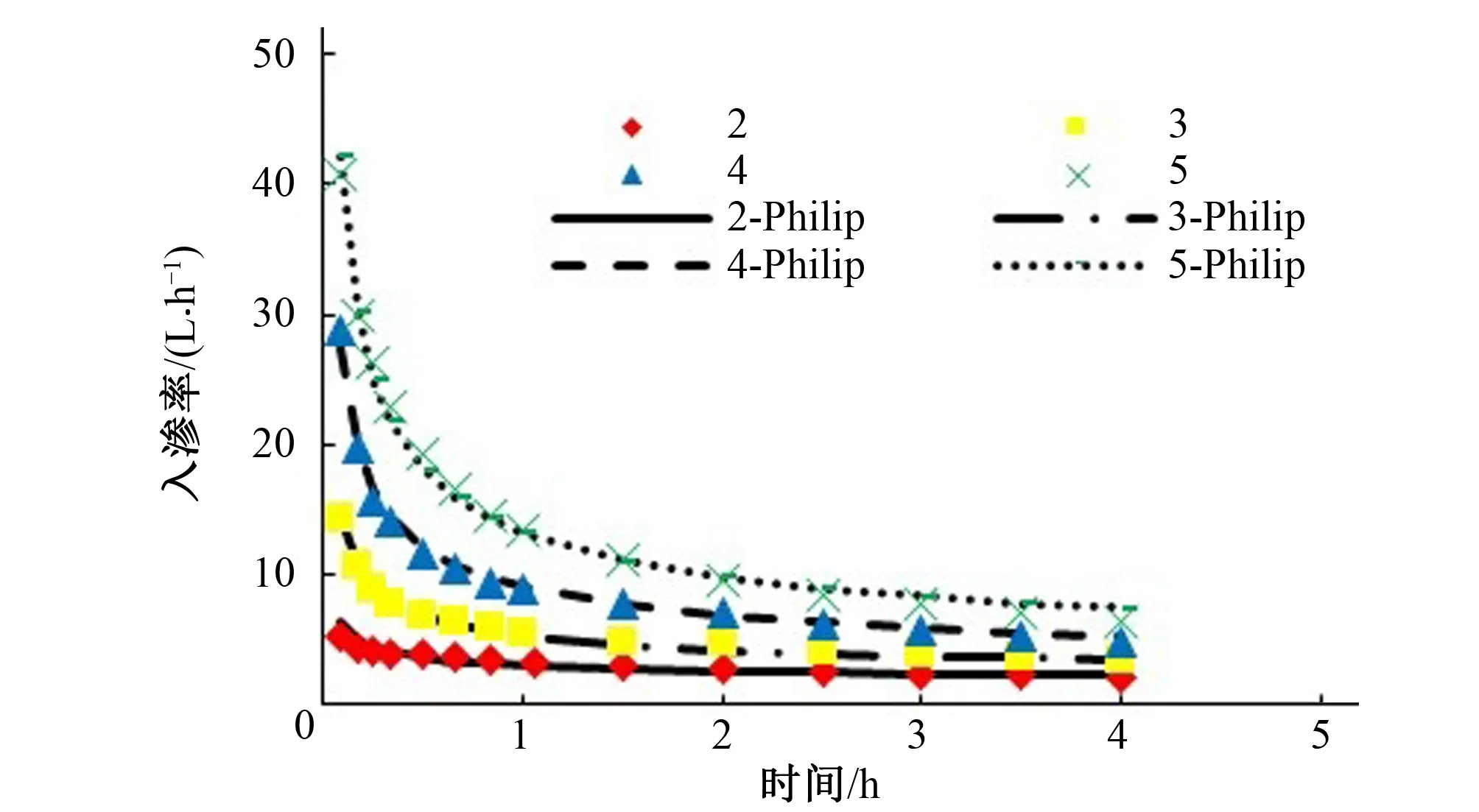
图4 Philip入渗模型不同线源直径下的入渗率

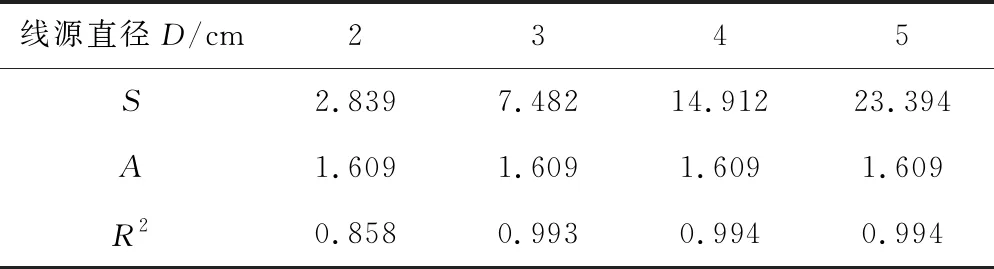
表2 Philip入渗模型不同线源直径下的参数表

由图4和表2可知，Philip入渗模型在不同线源直径下的决定系数R2均在0.858以上，说明Philip入渗模型模拟值与实测值接近，模拟精度较高，能真实地反映出不同线源直径的入渗率变化趋势。因此，Philip入渗模型能模拟不同线源直径下的入渗规律。

随着线源直径的增加，吸渗率S在增加，用线性函数对其进行拟合，拟合结果见图5。

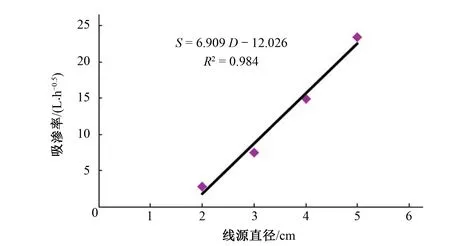
图5 Philip入渗模型吸渗率S与线源直径拟合关系

由图5可知，吸渗率S与线源直径拟合的决定系数R2为0.984，说明吸渗率S与线源直径的线性关系良好。则线源长度为30 cm，不同线源直径的Philip入渗模型为：

i(t)=0.5×(6.909D-12.026)t-0.5+1.609

(9)

I(t)=(6.909D-12.026)t0.5+1.609t

(10)

式(9)可简化为：

i(t)=(3.455D-6.013)t-0.5+1.609

(11)

由于i(t)和I(t)均不小于0，因此D不小于1.7 cm。

2.2.2 Kostiakov入渗公式对线源直径的适用性

将不同线源直径下实测入渗率用Kostiakov入渗公式进行模拟，模拟结果如图6和表3所示。图6是Kostiakov入渗公式不同线源直径下的入渗率，反映了Kostiakov入渗公式所模拟的入渗率和不同线源直径下实测入渗率的对比关系。表3是Kostiakov入渗公式不同线源直径下的参数。

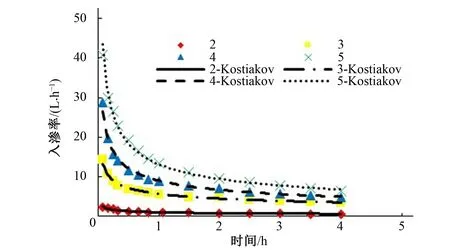
图6 Kostiakov入渗公式不同线源直径下的入渗率

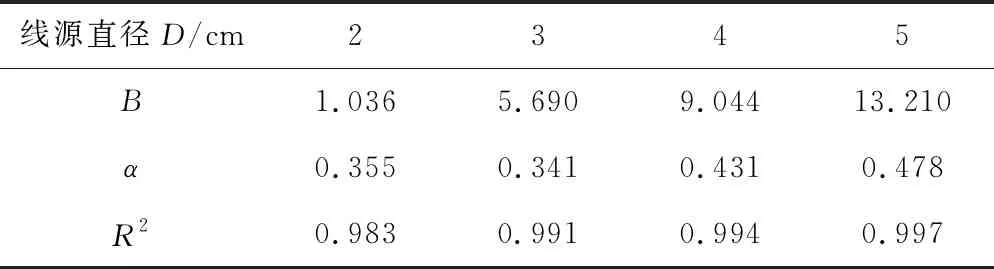
表3 Kostiakov入渗公式不同线源直径下的参数表

由图6和表3可知，Kostiakov入渗公式在不同线源直径下的决定系数 均在0.983以上，说明Kostiakov入渗公式模拟值与实测值更接近，模拟精度更高，更能真实地反映出不同线源直径的入渗率变化趋势。因此，Kostiakov入渗公式更能模拟不同线源直径下的入渗规律，而且略比Philip入渗模型精确。

随着线源直径的增加，参数B和参数α均增加，用线性函数对其进行拟合，拟合结果见图7。

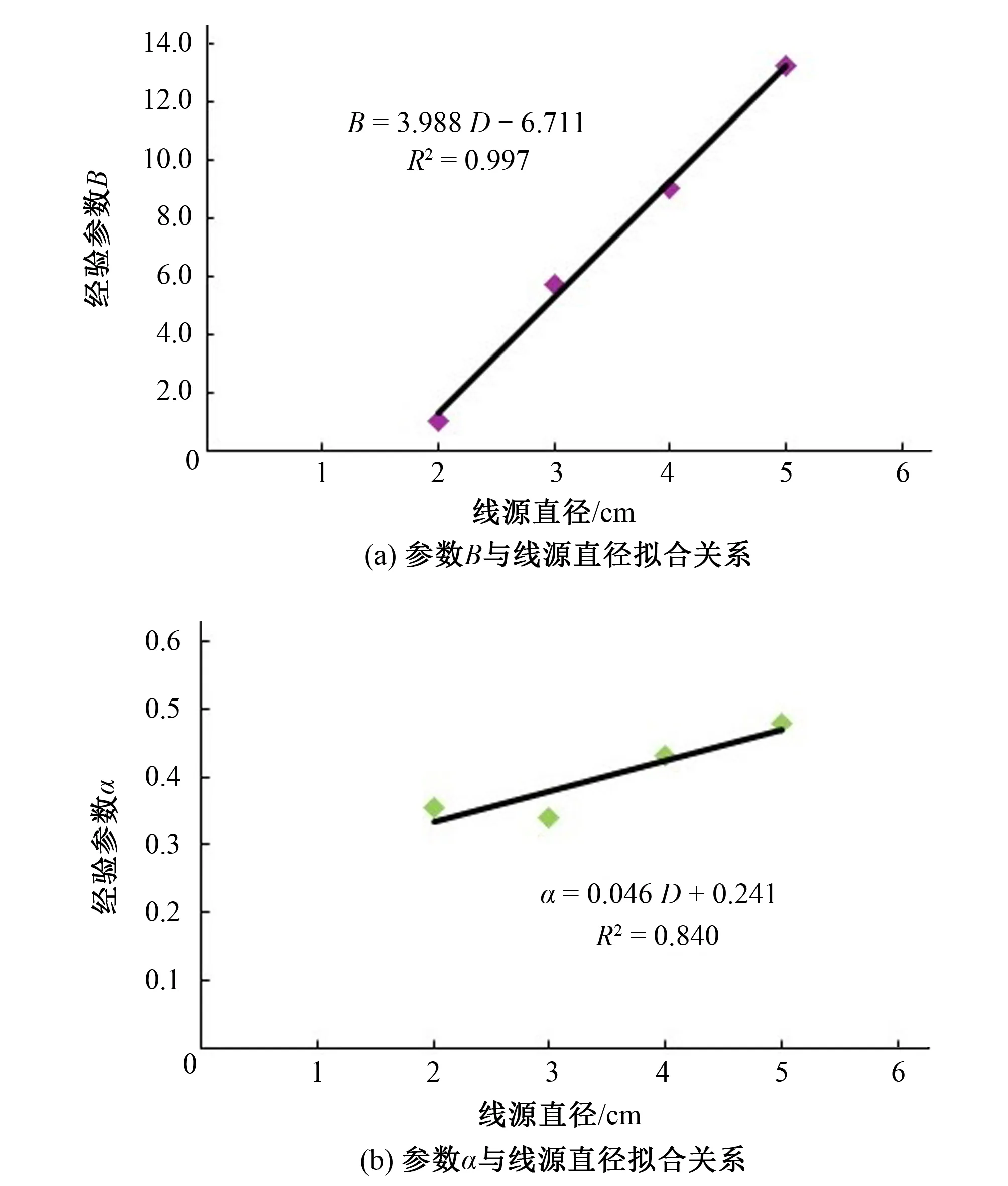
图7 Kostiakov入渗公式参数与线源直径拟合关系

由图7可知，参数B与线源直径拟合的决定系数R2为0.997，参数α与线源直径拟合的决定系数R2为0.84，说明参数B和参数α均与线源直径的线性关系良好。则线源长度为30 cm，不同线源直径的Kostiakov入渗公式为：

i(t)=(3.988D-6.711)t-(0.046 D+0.241 )

(12)

(13)

式(13)可简化为：

(14)

由于i(t)和I(t)均不小于0，因此1.7 cm≤D≤16.5 cm。

2.2.3 Horton(变形)入渗公式对线源直径的适用性

将不同线源直径下实测入渗率用Horton(变形)入渗公式进行模拟，模拟结果如图8和表4所示。图8反映了Horton(变形)入渗公式所模拟的入渗率和不同线源直径下实测入渗率的对比关系。

图8 Horton(变形)入渗公式不同线源直径下的入渗率

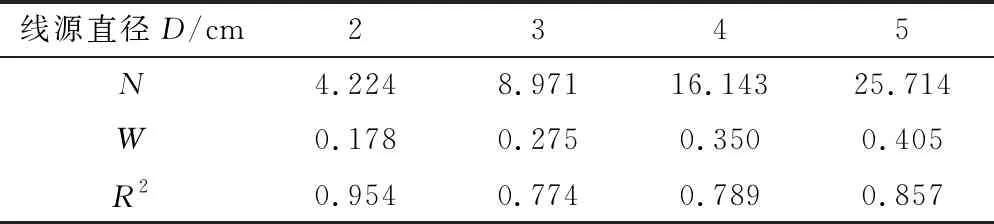
表4 Horton(变形)入渗公式不同线源直径下的参数表

由图8和表4可知，Horton(变形)入渗公式在不同线源直径下的决定系数R2均在0.774以上。说明Horton(变形)入渗公式拟合值与实测值较接近，能大致反映入渗率随时间变化趋势。因此，Horton(变形)入渗公式可以模拟不同线源直径下的入渗规律，但精确度低于Philip入渗模型和Kostiakov入渗公式。Horton(变形)入渗公式更适合于入渗中期和后期的模拟。

随着线源直径的增加，参数N和参数W均增加，用线性函数对其进行拟合，拟合结果见图9。

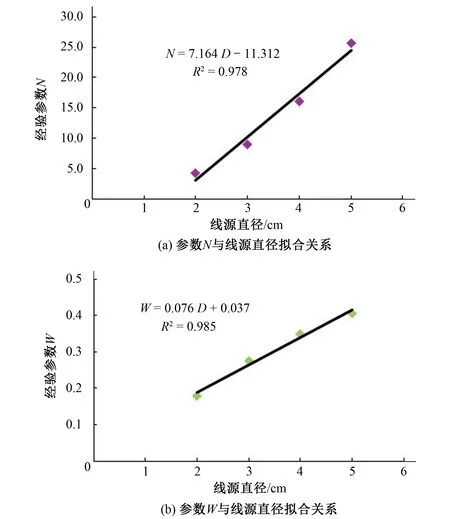
图9 Horton(变形)入渗公式参数与线源直径拟合关系

由图9可知，参数N与线源直径拟合的决定系数R2为0.978，参数W与线源直径拟合的决定系数R2为0.985，说明参数N和参数W均与线源直径的线性关系良好。则线源长度为30 cm，不同线源直径的Horton(变形)入渗公式为：

i(t)=(7.164D-11.312)e-(0.076 D+0.037)t

(15)

(16)

由于i(t)和I(t)均不小于0，因此D不小于1.6 cm。

3 结 论

本文在垂直线源供水条件下，研究了不同线源直径入渗率和累积入渗量的变化特性，并借助Philip入渗模型、Kostiakov入渗公式和Horton(变形)入渗公式对不同线源直径下入渗规律的适用性进行了分析比较，建立了经验公式，得出以下结论。

(1)不同线源直径的入渗率变化趋势基本一致，随着入渗历时的延长，入渗率均在降低，且降低幅度逐渐变缓，最终趋于稳定；线源直径对入渗率有明显影响，随着线源直径的增加，入渗率逐渐增大。

(2)不同线源直径的累积入渗量变化趋势基本一致，随着入渗历时的延长，累积入渗量均在增加，且增长幅度逐渐变缓；线源直径对累积入渗量有明显影响，随着线源直径的增加，累积入渗量逐渐增大。

(3)3种模型均能模拟不同线源直径下的入渗规律，Kostiakov入渗公式和Philip入渗模型较精确，Horton(变形)更适合于入渗中期和后期的模拟。

(4)得出不同线源直径下3种入渗模型的经验公式。