粘重土壤下马铃薯挖掘机分离输送装置优化与试验

赵胜雪，赵越，刘权磊，周东麟，潘思奇

（黑龙江八一农垦大学工程学院，大庆 163319）

马铃薯机械化收获作业是实现马铃薯全程机械化的作业基础与关键，是实现劳动效率增强、产量与效益增加的重要手段[1-3]。但我国寒地地区的土壤结构粘性较大，已有的马铃薯收获机械虽可以满足作业要求，但仍存在由于升运链与粘重土壤匹配适应性差导致运输效果不佳以及薯土分离装置效果差影响筛选分离作业[4-5]。因此国内外针对该问题进行相应的科学研究。国外针对马铃薯收获采用联合作业模式，该方式具有多种、多级的输送分离装置，薯土分离效果较好，但不适宜我国北方寒地地区粘重土壤环境与小地块作业环境[6-7]。而我国主要采用分段作业模式，其中升运链式马铃薯挖掘机是使用最普遍的机型，而升运链目前主要结构为单级和双级，其作用是利用抖动器增强薯土分离效果[8-10]。但我国研究学者针对升运链性能、抖动轮作业原理以及薯土分离效果的理论研究较少，未有效解决马铃薯收获作业时的明薯率偏低等问题。

目前，国内外针对机构优化设计与改进的方法大多采用正交或正交旋转试验设计进行试验设计方案，以此获取较为合理的马铃薯挖掘机分离输送装置结构参数，利用最小二乘法进行结构参数估计，并建立相应的数学关系式，即确定输入参数为机具前进速度、二级升运链长度和升运链线速度，将明薯率确定为评价指标，通过试验分析方法对数据进行处理与优化，找出最佳马铃薯挖掘机分离输送装置结构参数[11-12]。但存在计算精度差、局限性较大、处理能力不强等缺点。而农业机械在机构设计优化时，由于各部件之间存在多种交互影响，因此在马铃薯挖掘机分离输送装置的设计过程与实际作业时，应考虑各部件之间的交互作用，采用传统方法无法准确分析他们之间作用关系[13-14]。BP 神经网络方法是目前智能算法中研究热点，理论研究表明当隐含层数目足够时，三层神经网络能满足任意精度的非线性参数优化[15]。BP 神经网络的非线性映射能力已广泛应用于农业工程领域。王吉权在2011 年利用BP 神经网络方法预测了农机动力与年份之间关系，较为准确预测农机动力发展趋势[16]。董志贵等在2017 年通过BP 神经网络算法对联合收割机中的吸气压力进行损失优化研究，确定最佳工艺参数组合[17]。综上所述，BP 神经网络适合于马铃薯挖掘机分离输送装置的参数优化研究。

针对马铃薯挖掘机分离输送装置的结构进行优化，提出基于BP 神经网络的优化方法，设计适宜北方寒地粘重土壤条件下的马铃薯挖掘机输送分离装置。首先针对马铃薯挖掘机分离抛送装置、土壤打碎与筛分装置的原理进行理论分析，确定适宜的二级升运链尺寸与抖动器结构参数；其次建立关于明薯率的BP 神经网络模型，得出机车前进速度、二级升运链尺寸以及其线速度三者与明薯率间的函数关系，通过对结构参数进行优化确定最佳工作参数组合。设计的机械结构可以有效提高机具在粘重土壤条件下作业时的薯土分离效果，降低马铃薯收获作业的损伤，以及提出机械结构优化时的新方法，为其他机构优化设计的算法应用提供借鉴与参考。

1 试验设计

1.1 马铃薯挖掘装置明薯率影响因素分析

北方寒地粘重土壤条件下马铃薯收获作业时，为测定二级升运链结构马铃薯挖掘机输送分离装置的输送分离作业效果与性能时，分析主要影响薯土分离效果的因数指标，确定以机车前进速度、二级升运链尺寸以及其线速度作为试验因素，将明薯率作为评价指标，采用二次正交旋转组合试验方法作为试验设计方法。数据采集为随机取10 m 长的两行马铃薯试验区进行收获作业并测量，每组试验重复3 次。

1.2 试验设计

采用二次正交旋转方法作为试验设计方法，选用明薯率作为试验评价指标，试验因素间的水平范围：机车前进速度0.6～1.8 m·s-1、二级升运链尺寸2.5～4.5 m、二级升运链线速度0.8～2.4 m·s-1。通过分析试验结果得到影响评价指标的3 个因素的显著性，并对其组合参数进行优化，确定适宜的各因素间水平范围。试验因素水平编码如表1 所示。

表1 试验因素编码Table 1 Code of test factors

2 基于BP 神经网络的参数优化方法

2.1 构建BP 神经网络优化模型

2.1.1 BP 神经网络结构设计

利用MATLAB 中BP 神经网络方法建立马铃薯挖掘机输送分离装置参数优化模型。方法相比于传统非线性优化方法提高了拟合精度与精准性，是一种经典的监督式神经网络分类器，以实现非线性的映射函数关系与自学习求解功能[19-20]。神经网络上每层传递是需要神经元利用传递函数进行连接，同层神经元之间无联系[21]。

神经网络模型采用三层结构，即输入层、隐含层、输出层，建立关于马铃薯挖掘机输送分离装置参数优化模拟模型。模型中的输入层神经元为3 个，即机车前进速度、二级升运链尺寸以及其线速度；输出层神经元数量则为1 个，即马铃薯明薯率；神经元传递函数选用sigmoid 函数、训练函数采用trainbfg 函数。隐含层神经元节点数的计算公式为[22]：

式中：nh隐含层节点数；

ni—输入层节点数；no—输出层节点数；

l—（1，10）区间内的任意常数。

经计算，隐含层数在2～12 之间，根据网络性能测试确定隐含层数量为6，BP 神经网络结构图如图1所示：

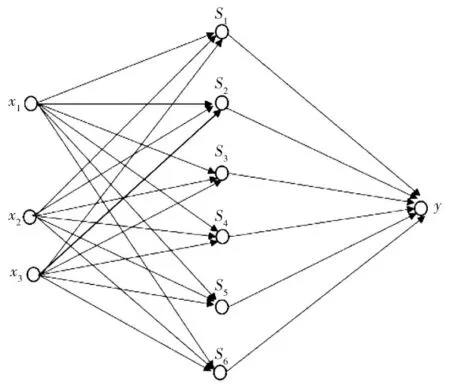
图1 BP 神经网络结构图Fig.1 Structure of BP neural network

马铃薯挖掘机输送分离装置参数优化的目标函数关系可表示为：

式中：Y—输出向量，Y=［y］；

f（）—BP 神经网络输入层到隐含层、隐含层到输出层的传递函数；

X—输入向量，X=［x1，x2，x3］T；

W—输入层与隐含层的权值矩阵；

V—隐含层与输出层的权值矩阵；

θ2—隐含层阈值；

θ2—输出层阈值。

2.1.2 数据归一化处理

神经网络中的数据输入与输出通常需要进行归一化处理，以消除量纲影响作用，满足传递函数的阈值范围，提高试验收敛速率。研究采用的归一化方法为MATLAB 中的Mapminmax 函数[23]。

采用归一化的方法对试验数据进行处理，T=［T1，T2，T3，T4］=［x1，x2，x3，y］。其区间为[a，b]，则输入与输出的数据归一化处理的计算公式为：

式中：Ti—训练样本中第i 个输入数据；

Tt′—Ti归一化后的数据，Tt′∈[a，b]；

Timax、Timin—训练样本中的第i 个数据的最大与最小值。

式（3）的逆变换公式为：

2.1.3 BP 神经网络的拟合

采用Matlab R2017b 软件编写总体系统学习率的BP 神经网络计算机程序，对归一处理后的数据样本进行拟合。其结构模型采用3-6-1 形式，归一化的数据区间为[0.2，0.7]，初始学习率选定为0.8，当输出的网络误差小于0.0464%时，输入层和隐含层间权值矩阵W 为：

2.2 马铃薯挖掘机分离装置机构参数全局预测与优化

2.2.1 优化方法

优化模型为非线性参数模型，在利用神经网络方法时，为调整权值时采用的方法为负梯度法，通过数据误差的自组织与反向传播、自适应、自学习及高映射能力提高模型精度。针对BP 神经网络模型优化方法采用的具体步骤如下：

（1）数据处理。将试验数据利用公式进行标准化处理，以实现消除量纲目的。

（2）确定马铃薯挖掘机分离装置机构参数的优化范围，通过分析其主效应图等，删除中间不显著的水平值，以缩小优化区间，降低优化工作量。

（3）建立马铃薯挖掘机分离装置机构参数的BP神经网络关系模型。确定的输出参数为机车前进速度、二级升运链长度、升运链线速度，通过改变模型中的隐含层数目、训练函数等设置，建立理想模型，且由于均方差（MSE）较方便，选此方法作为评价模型预测精准度的衡量标准。

（4）寻优搜索。利用神经网络方法具有高泛化能力对试验数据进行寻优搜索，经多次迭代，确定搜索的最佳结构组合参数。

（5）迭代次数确定。通过i 次迭代可以确定最优响应值Yi，但其未进行标准化为yi，根据公式（6）与公式整理可得：

2.2.2 优化的约束条件

试验根据设计时所设计的因素水平的上下限，马铃薯挖掘机分离装置结构参数优化的约束条件为：

2.3 网络训练

网络训练是针对隐含层进行数据训练。在输入层中定义原始分离装置结构参数数据序列为：

对数据进行标准化处理，依据如下公式：

式中：xnorm—标准化后的数据；

x—原始数据；

xmax、xmin—原始数据中最大值与最小值。

标准处理后的训练集、测试集为：

依据隐含层特点，构建输入短时序列，通过固定步长确定时间序列长度。设步长L，则模型输入为：

对应的理论输出为：

2.4 网络预测

选择均方根RMSE 作为误差计算公式：

式中：L（m-L）—训练样本总数；

Pi—预测值；

Yi—真实值。

网络预测方法采用迭代预测法，即当理论输出的L 个数据为YP=（x′m-L+1，x′m-L+2，…，x′m），而输入训练后的网络输出为PP=Pm+1。即m+z 时刻预测值为Pm+1，将最后L-1 个数据与测试集中的第m+1 个数据合并成新数据并输入网络，得到m+2 时刻输出数据Pm+2，以此类推得预测序列为：

3 结果与分析

3.1 试验方案结果

试验方案与试验结果如表2 所示。

3.2 不同优化方法的马铃薯明薯率拟合结果分析

根据表2 中的试验数据，影响因素马铃薯明薯率y 与评价指标二级升运链长度x1/m、机具前进速度x2/（m·s－1）、升运链线速度x3/（m·s－1）之间的二次回归方程为：

图2 所示为BP 神经网络模型的实际值与拟合值对比分析图，图3 为二次回归模型实际值与拟合值对比分析图。通过分析图2 与图3 可知，对比两种模型的R2可知，BP 神经网络模型的R2（0.98）大于二次回归模型的R2（0.923 3），而BP 神经网络模型的均方根误差（0.057%）小于二次回归模型的均方根误差（1.68%），表明BP 神经网络模型的拟合程度和精度均好于二次回归模型，因此运用BP 神经网络模型拟合函数能更真实反映试验因素与评价指标间的函数关系。

表2 试验方案与试验结果Table 2 Results of test scheme

3.3 田间验证试验

在黑龙江省农业科学院进行田间试验（4 hm2的黑黏土），试验材料为大西洋、克新19 马铃薯，采用旱地垄播形式，垄长500 m，垄宽800 mm，垄高280 mm，含水率20%，播深为150～300 mm。田间试验情况如图4 所示。

图2 BP 神经网络拟合值与试验值Fig.2 Fitting value and test value of BP neural network

图3 二次回归模型拟合值与试验值Fig.3 Fitting value and test value of quadratic regression model

图4 收获试验Fig.4 Harvest experiment

利用BP 神经网络模型作为目标函数对马铃薯挖掘机分离装置结构参数进行优化，得到最佳马铃薯挖掘机分离装置结构参数二级升运链长度2.5 m、机车前进速度1.793 9 m·s-1、升运链线速度0.8 m·s-1，该参数组合下马铃薯明薯率为99.7%。

并对二次回归模型拟合的回归方程进行优化，其方法是利用Design-Expert 8.0 6 优化软件。基于马铃薯实际收获作业时的性能与条件及分析结果，得出机车前进速度为1.06～1.6 m·s-1、二级升运链尺寸3.1～4.1 m 及其线速度1.36～1.6 m·s-1时，薯土分离性能最佳，该条件下的明薯率为98.1%～98.7%。

分析两种优化方法的试验结果，表明BP 神经网络模型优于二次回归模型拟合函数的RMSE、R2、P且明薯率也更高。由于优化问题属于黑箱问题，其优化解存在不确定性，不能准确判定两种优化结果的好坏。采用二次回归模型和BP 神经网络的优化方法对马铃薯挖掘机分离装置结构参数进行优化设计研究，均是建立在明薯率与分离装置各参数之间函数关系逼近的基础上。因此，理论认为相对平均误差小的拟合函数与真实函数更为接近，优化结果更令人信服、准确度更高。

4 结论

在BP 神经网络函数关系拟合的基础上，提出一种基于BP 神经网络的优化方法，并将其应用于马铃薯挖掘机分离装置结构参数的优化问题中，扩展了BP 神经网络方法的应用范围。

（1）提出BP 神经网络方法对马铃薯二级升运链式结构的分离输送装置进行优化设计，使其在粘重土壤条件下能满足作业要求。优化的试验参数为机车前进速度1.793 9 m·s-1、二级升运链尺寸2.5 m 以及其线速度0.8 m·s-1，该结构参数下进行收获作业得到的明薯率为99.7%，优化结果与实际结果间的相对误差仅为0.046 4%，表明基于BP 神经网络的优化方法的马铃薯挖掘机分离输送装置设计的可靠性。

（2）基于BP 神经网络的优化方法在马铃薯挖掘机分离装置结构参数优化上应用，对指导马铃薯收获作业、提高马铃薯产量、适宜北方粘重土壤作业具有重要的现实意义；同时，为解决农业机械中类似优化问题提供了一种思路。