固体火箭发动机振动夹具设计及动态特性分析

刘晓晨 陈坚 崔巍 吕萍 强科杰

固体火箭发动机振动夹具设计及动态特性分析

刘晓晨 陈坚 崔巍 吕萍 强科杰

（上海航天动力技术研究所, 浙江 湖州 313000）

振动试验是固体火箭发动机研制生产过程中不可或缺的环节，夹具设计在一定程度上决定了振动试验的精确度和可靠性。文中根据夹具设计规范，设计了某型号固体火箭发动机专用振动试验夹具，应用ANSYS WORKBENCH有限元软件对其进行了模态和随机振动仿真分析，并通过垂向振动加载试验完成了动态特性验证，结果表明：夹具的固有频率和振动放大因子均满足设计和使用要求；另外，基于动态特性的振动夹具设计方法可为今后类似结构设计和研究提供有效的参考。

夹具设计；有限元分析；振动试验；动态特性

0 引言

固体发动机作为各类飞行器的主流动力装置，在工作过程中承受着各类振动与冲击载荷，高可靠性和环境适应性成为固体发动机质量特性的关键[1]。振动试验是考核固体发动机环境适应能力的主要途径，不仅能够检验在交付使用过程中能否满足抗振性能要求，也能够暴露其在设计上的缺陷，从而为固体发动机的优化和改进提供指导。振动试验中，夹具的作用是将振动台的能量和运动传递至试验件，其振动传递特性的优劣将直接影响产品能否按照预定的要求接受振动考核。振动过程中，理想的情况是夹具能将振动台的能量不失真的传递给试验件，如果夹具的振动传递特性不佳，就会发生过试验或者欠试验的现象[1-2]。因此，开展振动夹具的传递特性分析对于系统的动态特性和试验质量具有重要意义。

目前，固体发动机振动夹具设计主要采用经验设计法，并通过成型夹具的振动试验方法验证结构的合理性，很难保证能够将振动台的能量不失真的传递给试验件，严重时还会因为试验后结构的不合理造成加工材料的浪费。近几年，诸多学者对振动夹具的结构设计开展了研究，通过有限元仿真方法获得了能够改善夹具动态特性的结构模态参数[2-4]。然而，针对夹具的传递特性分析多采用试验方法进行，而基于有限元方法的夹具动态特性研究尚未推广至工程应用。针对上述问题，王红瑞等[3]在对比分析3种振动夹具动态特性过程中提出：基于动态特性设计的夹具能更好的保证振动能量不失真的传递。马爱军[5]在研究试验条件下的振动夹具动态设计过程中着重强调能够表征振动的动态特性量（振动传递率、放大因子、共振频率等）概念，并提出振动试验是一个动态过程，夹具设计只考虑静刚度要求是不够的，需要采用有限元方法对夹具在振动试验条件下的动态特性加以深入分析。

本文根据固体发动机振动试验要求，旨在开展夹具设计及其模态和振动传递特性分析，并通过将有限元仿真结果与振动试验结果进行对比，验证基于振动传递特性的夹具设计方法的有效性，为固体发动机振动夹具的有效性设计提供指导。

1 模态与振动传递特性理论

1.1 模态理论分析

模态能够表征夹具的振动特性，研究夹具振动特性首先需要对其进行模态分析，简而言之就是通过数值计算或试验的方法，获得夹具的固有频率、阵型和阻尼比等结构模态参数[6]。严格意义上，振动夹具是一个连续的弹性体，采用有限元的方法，能够将连续弹性体的振动问题离散为研究多自由度系统的振动问题。因此，振动夹具的运动微分方程可以表示为

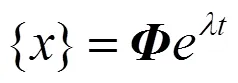
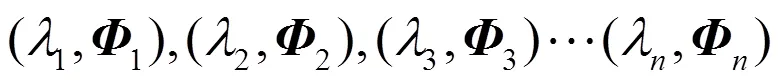
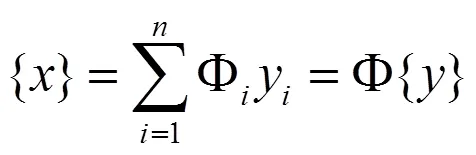
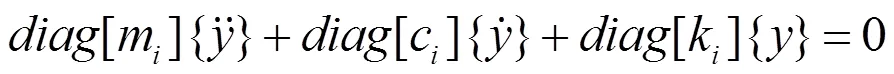
代入初始条件，可解得夹具的振动规律为

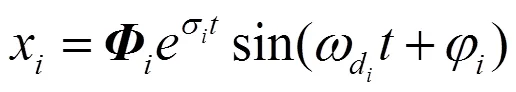
1.2 振动传递特性理论

其中，夹具上的振动传递率为

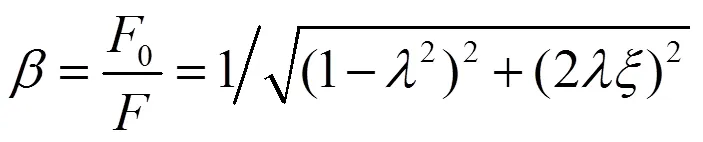
图1 振动传递特性曲线

2 振动夹具建模

本文针对某小型特种固体火箭发动机，应用PROE软件对发动机的振动试验夹具进行了设计和三维建模。夹具由底板、下卡箍和上卡箍组成，材料均为45#结构钢，整体尺寸为430mm×430mm×150mm。其中，底板与下卡箍通过焊接成型，上卡箍与下卡箍直接通过螺纹紧固，底板通过螺栓直接与振动台动圈连接，装配后的三维模型如图2所示。

合理的模型是有限元分析的基础，模型的好坏将直接影响结果的准确性[7]。振动试验过程中，夹具底板通过螺栓直接与动圈连接而不发生相对移动，可以认为夹具与振动台动圈保持刚性连接。由圣维南定理可知，模型中细小的特征将对结构整体性能和分析效率产生很大的影响[8]。振动夹具中存在一些螺纹孔，因此分析过程中对这些螺纹孔特征进行忽略。将简化后的夹具三维模型导入到ANSYSY WORKBENCH中，并对导入后的装配体进行零件整合，使其转化为一个组件，意义在于不仅能够省去不必要的接触设置，还能使得网格划分时进行一体化整体划分，不同构件连接位置共节点，通过两个面共享一部分节点实现位移和力的传递[9]。

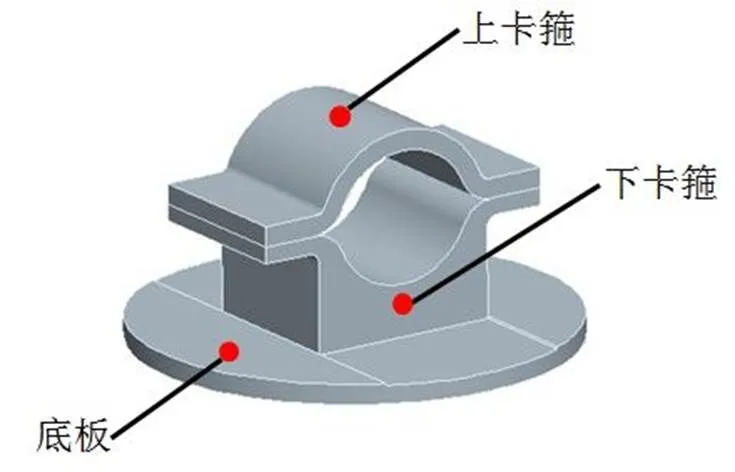
图2 振动夹具结构示意图

图3 振动夹具有限元模型

夹具有限元网格划分以六面体单元为主，局部采用五面体单元。由于夹具结构最小尺寸为10mm，同时考虑到计算机分析能力和计算效率，定义网格单元尺寸为3mm，满足划分网格单元尺寸小于最小尺寸的1/3，网格节点和单元数分别为100314和40617，网格划分后的有限元模型如图3所示。振动试验时夹具通过底板与振动台动圈机械连接，为了模拟夹具振动试验工况，夹具的边界条件设置为在底板的下表面添加固定约束。

3 结构动力学仿真试验及结果分析

3.1 模态分析

模态分析是振动夹具设计的必要环节，也是结构动力学分析的基础，根据分析目的和工况的不同，模态分析可分为自由模态分析和添加边界条件的普通模态分析[3,10]。振动试验夹具的设计准则要求夹具的1阶固有频率高于试件1阶固有频率的3-5倍，避免夹具与试件间发生系统耦合共振。通过模态分析可以求得振动夹具多阶固有频率和阵型，对于夹具设计的合理性判定具有重要意义。

本文设计的夹具为单向振动试验夹具，振动试验过程中，夹具连接试验件只承受Y方向的振动载荷。试验频率范围为10-2000Hz，故对夹具进行模态分析时提取Y方向的阵型和固有频率，查看夹具在振动方向上的变形情况。经模态分析可知，夹具在2000Hz内共有2阶模态，第3阶模态频率为2013Hz，如图4所示，因此提取夹具的前2阶模态加入随机振动仿真分析中。

图4 振动夹具模态频率

图5 1阶Y向模态阵型

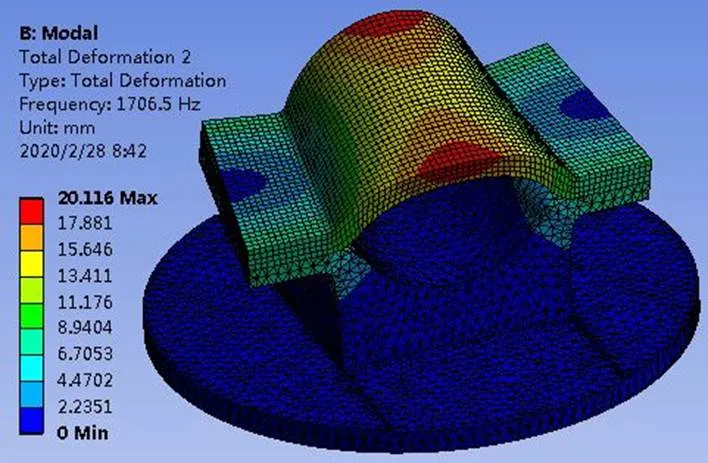
图6 2阶Y向模态阵型

图7 3阶Y向模态阵型

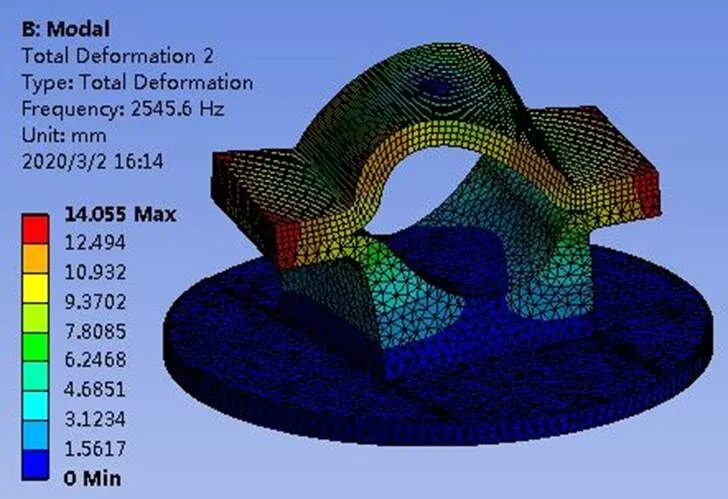
图8 4阶Y向模态阵型

经模态分析可知，振动夹具1阶模态频率为1251.2Hz，由于该夹具所对应固体发动机的1阶模态频率约为350Hz，满足振动夹具1阶模态频率大于试验件1阶模态频率的3倍。振动夹具的1-4阶Y向模态阵型如图5-8所示：其中，第1阶Y向模态阵型中最大变形发生在上卡箍与下卡箍的连接位置，表现为沿X方向的弯曲变形，但夹具整体变形量较小；第2阶Y向模态阵型表现为上环箍沿X方向的弯曲变形；第3和4阶Y向模态阵型表现为上卡箍的扭转变形。夹具在试验频率10-2000Hz范围内共有2阶模态，虽然1阶模态频率较高，满足大于试验件1阶模态频率的3倍，但由于试验最高频率为2000Hz，因此很难做到在试验频率范围内夹具没有模态频率。然而，只要做到夹具的振动放大因子尽可能的小，即传递特性足够合理，夹具的设计同样满足使用要求[11]。夹具的模态阵型主要表现为X方向的横向变形，主振方向Y上的振动变形较小，这说明从结构设计而言，夹具的设计比较合理，初步判定可用于发动机Y方向上的振动试验夹持。

3.2 随机振动仿真分析

模态分析只能提取到夹具的模态频率和阵型，可以初步判定夹具设计的合理性，但无法得知夹具在振动工况下的具体响应情况，因此还需要对夹具进行随机振动响应分析，得到夹具在随机振动下的加速度均方根响应分布[9,12,13]。本文在模态分析的基础上，给夹具施加如图9所示Y方向上的随机振动载荷，载荷输入采用基础约束进行加载，具体加速度功率谱密度曲线如图10所示，加速度均方根值为13.09g。

图9 随机振动载荷方向示意图

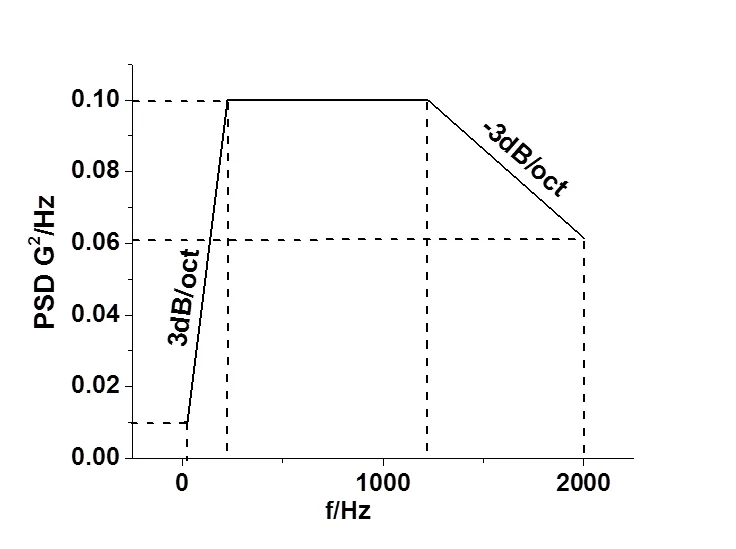
图10 加速度功率谱密度曲线

应用ANSYSY WORKBENCH中的RANDOM VIBRATION模块对夹具进行随机振动响应分析，由于振动夹具采用结构钢焊接而成，整体刚性较好，故根据经验设置模态阻尼为0.02。通过对夹具施加Y方向的随机振动载荷，得到如图11所示的夹具整体位移和应力云图。由仿真结果可知，夹具上最大位移0.003 mm出现在上环箍的顶部位置，夹具的最大应力为6.22 MPa远小于45#钢的屈服强度355 MPa，因此夹具的强度承载能力足够，该夹具的设计强度满足要求。

工程实际中，往往比较关心夹具与试验件直接接触部位的响应传递情况。此外，振动试验中常选择振动夹具底盘的上表面设置振动控制点，底盘上表面与其下表面对应位置的响应基本一致。因此，上述这些部位的响应情况将在一定程度上直接决定了夹具传递特性的好坏。为了分析夹具的Y向振动传递特性，共选取夹具上三个测点，其中，A、B两点作为响应监测点，O点作为响应对照点，如图12所示为夹具上测点分布情况。通过随机振动仿真得到所有测点Y向振动的均方根值及放大因子如表1所示，夹具整体的加速度分布云图如图13所示。

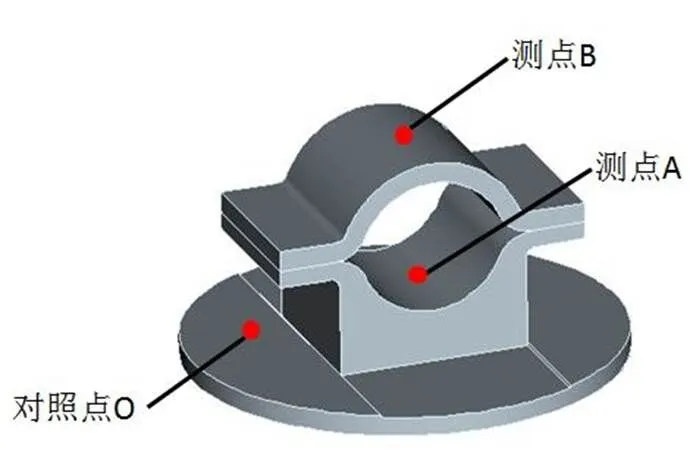
图12 测点分布与标注

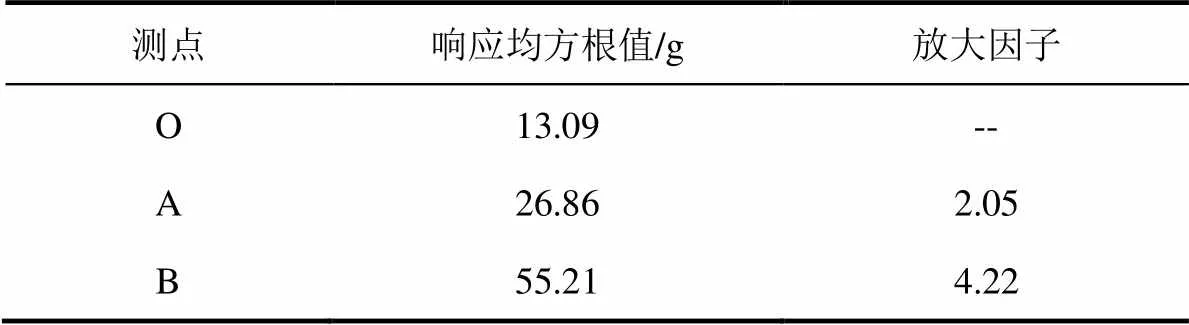
表1 测点均方根值和放大因子

图13 加速度分布云图

由随机振动仿真分析结果可知：振动夹具的整体结构中，底盘和下环箍的振动响应相对上环箍较小，最大振动响应发生在上环箍与试验件接触处的顶端；对照点O的响应均方根值为13.08 g，与输入的基础激励基本一致；响应点B的响应均方根值为55.21 g，放大因子为4.22，与加速度分布云图中最大加速度53.44g相接近，因此可以认为该夹具最大的放大因子为4.22；由夹具设计准则可知，放大因子越小，越有利于振动试验过程中对共振频率的抑制，该夹具最大放大因子满足小于5，因此夹具的振动传递性设计满足要求。

4 垂向振动加载试验

为了对加工成型的振动夹具进行动态特性有效验证，需要完成夹具的垂向（Y向）振动加载试验，考察夹具结构的固有频率、传递性、各点响应的均匀性等指标是否满足设计和使用要求。振动夹具垂向振动加载试验包括正弦扫频振动试验和随机振动试验两部分。正弦扫频试验的目的在于了解不同试验条件下夹具的共振频率，验证有限元模态分析结果的正确性。随机振动试验用来测试夹具在工作状态下的振动特性，验证夹具设计的合理性。

4.1 试验方法

通过有限元软件对振动夹具仿真分析后，对螺纹孔等细微处经过多次迭代计算，确定夹具的设计结构并按照流程安排加工。夹具整体采用45#结构钢焊接而成，总体质量为15.3kg。垂向振动加载试验中除了研究对象振动夹具外还包括以下设备：1）DL公司生产的振动台，振动频率范围2-2100Hz；2）8通道VR振动控制仪；3）PCB加速度传感器；4）计算机。试验系统的组成框图如图14所示。

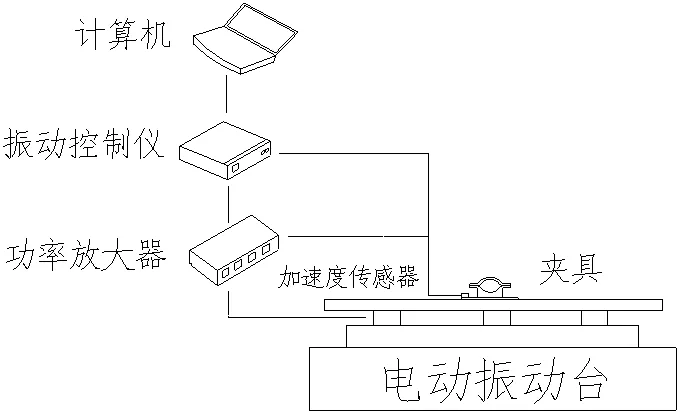
图14试验系统的组成框图

振动试验中选取O点作为控制点进行单点控制，选取A、B两点作为响应监测点，传感器布置位置与3.2节随机振动仿真分析中测点位置一致，图15是垂向振动加载试验的现场图。

图15 垂向振动加载试验现场图

4.2 扫频试验

首先对夹具进行正弦扫频振动试验，设置峰值加速度为0.3g。图16所示为扫频试验的振动控制和响应曲线，由此可见，10-1100Hz频率区间内控制曲线平坦，与输入目标曲线接近重合。根据各测点的频响曲线和传递率曲线可知，夹具的1阶固有频率为1183Hz，与3.1节仿真分析的的1阶固有频率1251.2Hz相比，二者相对误差为5.7%；夹具的2阶固有频率为1666Hz，与3.1节仿真分析的2阶固有频率1706Hz相比，二者相对误差为2.4%。由此看来，通过正弦扫频振动提取夹具固有频率的方法与有限元模态分析获取的结果具有一定的偏差，其原因除了与模型的精确性有关，还与仿真过程中施加边界条件的真实性相关。另外，严格意义上讲，正弦扫频振动获取的应该是夹具与振动台组成的系统整体的固有频率，但由于这种提取方法方便易操作，且与有限元模态分析结果间的偏差不是太大，所以可作为粗略获取夹具的共振频率的手段。

4.3 随机振动试验

随机振动试验载荷谱按照GJB150.16A规定的试验内容，载入与3.2节随机振动仿真相同的加速度功率谱密度。图17为随机振动试验的控制曲线，可知控制曲线平稳，在整个加载频带内，绝大多数控制曲线在允许的+3dB容差范围内，满足试验的控制要求。

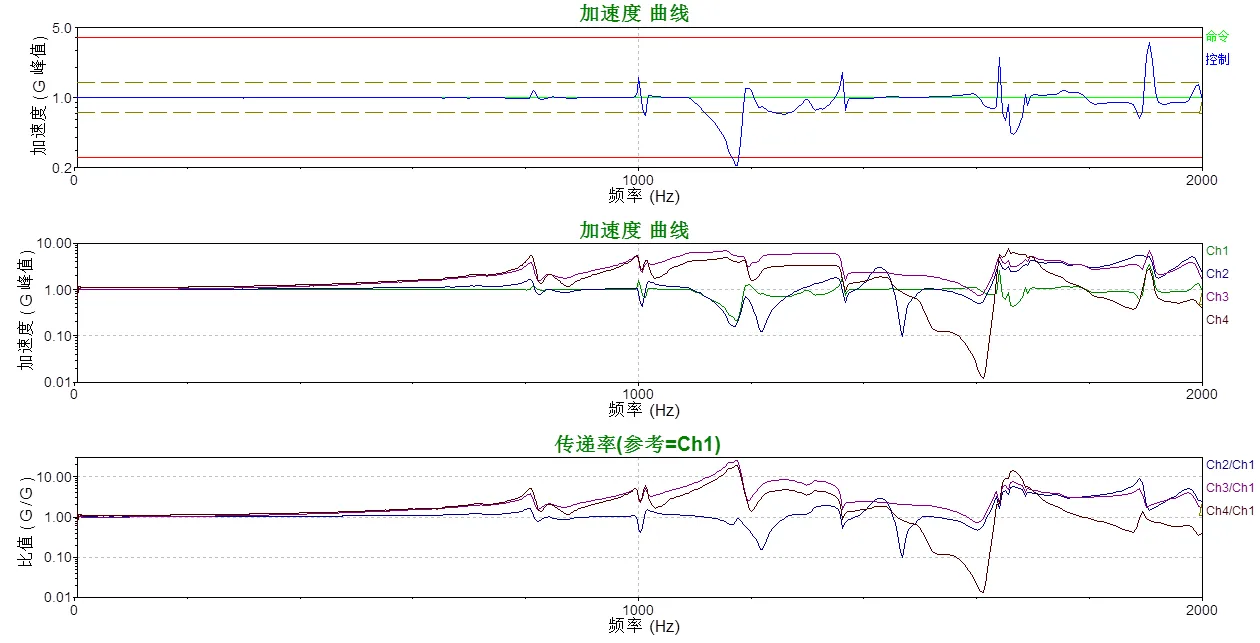
图16 正弦扫频试验曲线图

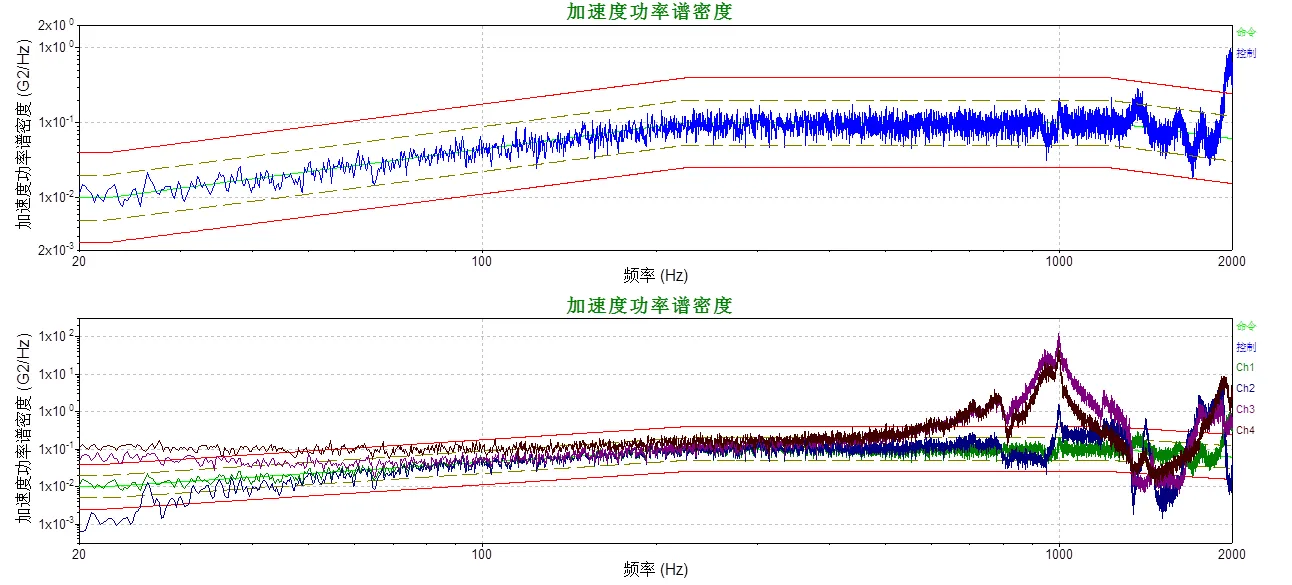
图17 随机振动试验控制和响应曲线图

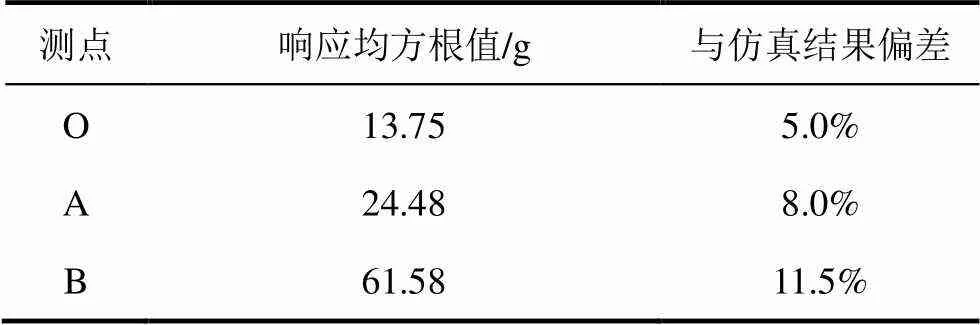
表2 试验结果及与仿真结果偏差

由随机振动试验结果可知：测点O的响应均方根值为13.75g，与仿真结果的偏差为5%，与输入的基础激励相比，测点O的放大因子为1.05；三个测点中，测点B的响应均方根值最大，与仿真结果的偏差为11.5%；通过3.2节随机振动仿真分析可知，测点B的响应与夹具上最大响应基本一致，可以近似认为测点B是夹具上响应放大最大的位置。随机振动试验中测点B的放大因子为4.70，由夹具设计准则可知，该夹具实际最大放大因子满足小于5，因此夹具的振动传递性满足使用要求。

通过与仿真分析结果对比发现，测点B的振动量值相对O、A测点大许多，主要是因为夹具的上下卡箍是通过螺栓紧固，而随机振动试验过程中没有试验件对上下卡箍进行接触连接，因此，不考虑试验件的单纯夹具振动试验在一定程度上会导致夹具顶部的响应放大；O、A、B三个测点的最大加速度响应和均方根值均与仿真结果具有一定的偏差，原因在于仿真分析中的基础激励是直接加载在夹具底面上，而振动试验中夹具是通过12颗周向螺栓与动圈上的螺栓孔连接，因此随机振动载荷是通过螺栓传递至夹具上的螺栓孔；此外，仿真分析中模型构建的简化过程，尚未对模型实际的弹性模量和阻尼进行测试。

5 结语

本文针对某特种小型固体火箭发动机的振动考核试验设计了对应夹具，并对其进行了有限元分析和垂向振动加载验证试验，基于振动传递特性证明了设计结构的合理性，结果表明：1）夹具的一阶固有频率为1251.2Hz，最大振动放大因子为4.7，各测点的振动量值在规定的范围内，满足夹具设计规范要求。2）基于动态传递特性设计的夹具结构满足使用要求，放大因子是评估夹具结构设计合理性的重要依据。3）仿真分析能够在正式试验前预测夹具结构的动态特性，减少不合理结构的样机加工。有限元理论分析和振动验证试验的设计论证流程合理有效，可以为其他类似结构的振动夹具设计提供参考。

[1] 钟继根, 王东升, 任万发, 等. 某导弹发动机振动试验夹具设计[J]. 振动工程学报, 2004,17(z2): 728-730. [Zhong Jigen, Wang Dongsheng, Ren Wanfa, et al. Design of Vibration Test Fixture for a Missile Engine[J]. Journal of vibration engineering, 2004, 17(z2): 728-730.]

[2] 李杰, 崔修斌, 林俊, 等. 某卫星资源舱试验夹具的有限元模态分析[J]. 环境技术, 2015(6): 23-26.[LI Jie, CUI Xiu-bin, LIN Jun, The FEM Modal Analysis of Welded Test Jig of Satellite Resource Cabin[J]. Environmental Technology, 2015(6): 23-26.]

[3] 王红瑞, 曹小娟, 尹韶平, 等. 鱼雷舱段振动夹具动态特性仿真分析[J]. 水下无人系统学报, 2018, 26(6): 549-554.[ Hong-rui, CAO Xiao-juan, YIN Shao-ping, et al. Simulation Analysis on Dynamic Characteristics of Fixture for Torpedo Cabin Vibration Test[J]. Journal of Unmanned Undersea Systems,, 2018, 26(6): 549-554]

[4] 杭超, 燕群, 张昕, 等.细长偏心舱体振动试验夹具设计分析与验证[J]. 机械科学与技术, 2019,38(2): 322-328.[Hang Chao, Yan Qun, Zhang Xin.Design and Validation of Fixture for Slender Off-centre Pod in Vibration Test[J].Mechanical Science and Technology for Aerospace Engineering, 2019, 38(2): 322-328.]

[5] 马爱军, 刘洪英, 董睿, 等. 振动试验条件在夹具动态特性设计中的考虑[J].航天器环境工程, 2013,30(1): 78-81. [Ma Aijun, Liu Hongying, Dong Rui, et al. Vibration environmental test conditions in fixture dynamic characteristic design[J]. Spacecraft Environment Engineering, 2013, 30(1): 78-81.]

[6] 倪振华. 振动力学[M].西安: 西安交通大学出版社, 1989: 196-203.

[7] 王世辉, 张昱, 陈欣欣, 等. 固体火箭发动机振动试验夹具优化分析与研究[J].计算机测量与控制, 2017,25(1): 221-223.[Wang Shihui, Zhang Yu, Chen Xinxin, et al. Vibration Test Fixture Optimization Analysis and Control for Solid Rocket Motor[J]. Computer Measurement & Control, 2017,25(1): 221-223.]

[8] 邹广平, 刘泽, 刘松, 等.金属橡胶减振器随机振动有限元仿真[J].中国机械工程, 2016,27(14): 1960-1963.[Zou Guangping,Liu Ze,Liu Song, et al.Finite Element Simulation of Metal Rubber Damper Random Vibration[J].China Mechanical Engineering, 2016,27(14): 1960-1963.]

[9] 王朋. 某大型振动试验工装研究[J]. 电子机械工程, 2016,32(5): 16-19.[WANG Peng. Research on a Large-scale Vibration Test Fixture[J]. Electro-Mechanical Engineering, , 2016,32(5): 16-19.]

[10] 高喆, 张玉方, 刘宁宁, 等.机载光电吊舱垂向振动工装设计[J].电视技术, 2019, 43(5): 98-102.[GAO Zhe;ZHANG Yufang;LIU Ningning, et al.Design of vertical vibration tool for airborne photoelectric pod[J].Video Engineering, 2019, 43(5): 98-102.]

[11] 王东升, 任万发, 刘青林, 等. 振动试验夹具共振频率设计要求研究[J]. 航天器环境工程, 2014,31(1): 37-41.[Wang Dongsheng, Ren Wanfa, Liu Qinglin, et al. The design requirements of the resonance frequency of vibration test fixtures [J].Spacecraft Environment Engineering, 2014, 31(1): 37-41.]

[12] 孙忠涛, 车英. 振动试验台夹具设计及频率响应特性研究[J].长春理工大学学报, 2010,33(2): 61-67.[SUN Zhongtao,CHE Ying.Research on Design of Vibration Fixture and Its Frequency Response Characteristic[J]. Journal of Changchun University of Science and Technology, 2010, 33(2): 61-67.]

[13] 李振鹏, 丁杰, 王永胜, 等. 控制箱夹具传递特性及对振动信号失真的影响分析 [J]. 航天器环境工程, 2017,34(6): 642-648. [LI Zhenpeng, DING Jie, WANG Yongsheng, et al. Transfer characteristics and influence analysis on vibration signal distortion of control box fixture[J]. Spacecraft Environment Engineering, 2017, 34(6): 642-648.]

Design and Analysis of Dynamic Characteristics of Vibration Fixture with Solid Propellant Rocket Engine

LIU Xiao-chen CHEN Jian CUI Wei LV Ping QIANG Ke-jie

（Shanghai Space Propulsion Technology Research Institute, Huzhou 313000，Zhejiang，China）

Vibration test is a indispensable part of the development and production of solid propellant rocket engine, and the design of the fixture determines the accuracy and reliability of the vibration test to a certain extent. In this paper, a vibration test fixture of solid propellant rocket engine was designed according to the fixture design specifications .and then modal analysis and random vibration simulation analysis of the solid propellant rocket engine were performed using workbench finite element analysis software. Finally, the dynamic characteristics verification was completed through the vertical vibration loading test. Results show that both the natural frequency and the vibration amplification factor of the fixture meet the design and use requirements. In addition, the dynamic characteristics can provide an effective reference for similar structural design and research in the future.

fixture design; finite element analysis; vibration test; dynamic characteristic

V435.6

A

1006-3919(2020)02-0056-08

10.19447/j.cnki.11-1773/v.2020.02.009

2020-02-23；

2020-04-07

刘晓晨（1991—），男，山东枣庄人，硕士，助理工程师，研究方向：固体火箭发动机力学环境试验及动力学技术研究；（313000）上海航天动力技术研究所.