差分隐私保护下的Adam优化算法研究

李 敏 李红娇 陈 杰

(上海电力学院计算机科学与技术学院 上海 200090)

0 引 言

神经网络在图像分类、语音分析和生物医学等领域应用广泛并且取得了显著的成果。但是用于训练神经网络的数据集通常可能包含各种各样的敏感信息，特别是目前云存储和云计算的发展使得大量数据存在隐私安全隐患。

目前，神经网络的优化算法隐私泄露原因与保护方法主要有：(1) 实际训练中由于数据量不够大导致模型易受到对抗攻击而造成的隐私泄露。Reza等[1]在2015年提出了一种采用协作式方法来训练模型的数据隐私保护方法，即让各个用户分别在各自的数据集上训练深度学习模型，并且有的放矢地将各自的模型参数互相共享。(2) 利用算法的过拟合缺陷，通过梯度下降技术和置信度来重现模型训练的数据导致隐私泄露的模型反演攻击[2]。Xie等[3]提出了使用同态加密数据，即将数据加密后再进行处理。Phan等[5]提出差分隐私自编码(ε-differential private autoencoder)，利用差分隐私理论来扰乱深度自编码器的目标函数，在数据重建过程中添加噪声从而保护数据。Shokri等[6]提出了基于分布式随机梯度下降的隐私保护方法，该方法假设各方分别训练各自的模型，不共享数据，仅在训练期间交换中间参数并且提供差分隐私保护。Abadi等[7]结合差分隐私理论提出了DP-SGD,优点是在适当的隐私预算内提供了较好的隐私保护程度，缺点是噪声对模型精度的影响较大。(3) 基于GAN的数据重现导致的隐私泄露。Papernot等[8]在2017年对保护训练数据隐私的机器学习模型进行改进，提出了Teacher-student模型。通过学习不同敏感数据集来训练不公开的teacher模型，teacher模型再对公开的未标记的非敏感数据进行预测，用于训练student模型，student模型不依赖敏感数据集，即使攻击者得到了student模型的参数也无法获取敏感数据的信息。

为了在神经网络优化算法的优化过程中实现差分隐私保护，本文提出差分隐私保护下的Adam优化算法(DP-Adam)。结合差分隐私理论，在神经网络训练的反向传播过程使用Adam优化算法并且利用指数加权平均思想来实现对深度学习优化算法的隐私保护，不但提高了模型精度，而且其隐私保护效果更好。实验表明，对于相同的隐私预算，随着训练时间的增加，DP-Adam训练模型的精度优于DP-SGD。除此之外，在达到同样模型精度的条件下，DP-Adam所需要的隐私预算更小，即DP-Adam的隐私保护程度比DP-SGD更高。

1 背 景

1.1 差分隐私

Dwork[10]于2006年首次提出了差分隐私这一概念。其主要思想是如果某个数据记录是否存在于数据集对于该数据集的查询或计算结果几乎没有影响，那么该记录就得到了差分隐私保护。因此，当该记录被加到数据集中时所造成的隐私泄露风险在某个可接受的范围内时，攻击者就无法获取该记录的准确信息，从而该记录得到保护。

定义1邻近数据集[10]若存在两个结构和属性相同的数据集D和D′,有且仅有一条记录不同，则这两个数据集称为邻近数据集。如表1所示，数据集d和d′是邻近数据集。

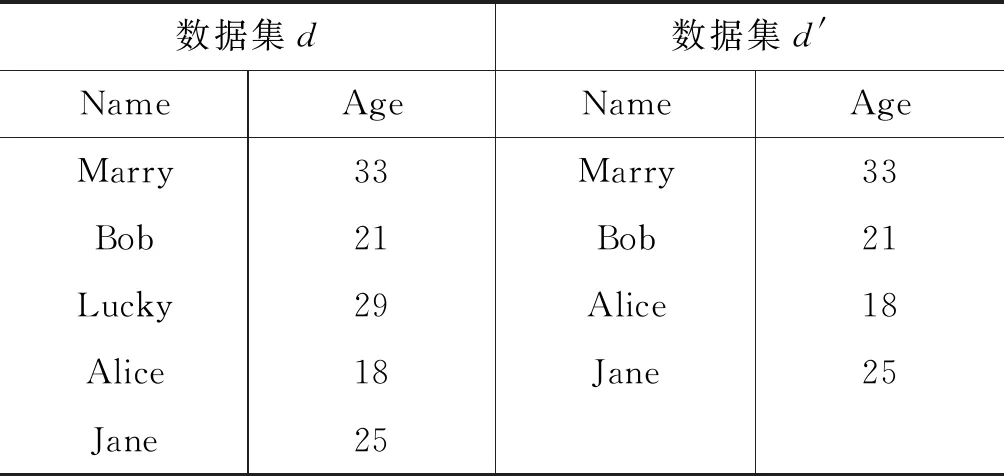
表1 邻近数据集d和d′

定义2ε-差分隐私[11]对于一个随机算法M:D→R,两个邻近数据集d,d′∈D,且M的任意输出S⊆R,若满足以下条件：

Pr[M(d)∈S]≤eε·Pr·[M(d′)∈S]

(1)

则算法M满足ε-差分隐私。式中：Pr表示概率；ε表示隐私保护预算，ε的值越小，隐私保护程度越高[12]。

从式(1)来看，隐私保护预算ε[13]表达的是算法M在邻近数据集d和d′上得到相同结果的概率之比的对数值，作用是衡量算法M所提供的隐私保护水平。理论上，ε的取值越小，则提供的隐私保护水平越高。但是数据的可用性也会随之降低。因此，ε的取值要平衡数据的隐私性和可用性。

定义3拉普拉斯噪声机制[14]拉普拉斯噪声机制的定义如下：

M(d)=f(d)+Lap(μ,b)

(2)

式中：位置参数μ,尺度参数为b的拉普拉斯分布Lap(μ,b)的概率密度函数如下：

(3)

当添加位置参数μ=0，尺度参数b=Δf/ε的拉普拉斯噪声时，式(2)则变为:

M(d)=f(d)+Lap(Δf/ε)

(4)

式中：敏感度Δf=|f(d)-f(d′)|;M是深度学习算法;f:D→R是分布函数;Lap(Δf/ε)是服从尺度参数为Δf/ε的拉普拉斯分布。由图1可知，ε越小，则b就越大，引入的噪声就越大。

图1 μ=0的拉普拉斯分布图

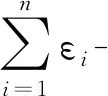
性质2并行组合性[15]设算法M1，M2，…，Mn,其隐私保护预算分别是ε1，ε2，…，εn,则对于不相交的数据集D1，D2，…，Dn,由这些算法组合成的算法M1(D1)，M2(D2)，…，Mn(Dn)提供(max εi)-差分隐私保护。

1.2 神经网络与Adam算法

神经网络是一种模仿动物神经网络行为特征进行信息处理的数学算法模型，基本组成单元是神经元。深度神经网络是由多层神经元组成，其结构如图2所示，“○”代表神经元，每一层神经网络都由若干个神经元组成，xi代表输入数据的特征向量，y代表输出结果的预测值。隐藏层越多，神经网络结构越复杂，训练得到的模型性能越好。因此，在训练超大的数据集和复杂度高的模型时，一般都需要构建隐藏层数较多的神经网络，但也要根据自身的研究目的设计合理的隐藏层数的神经网络，否则会导致过拟合。

图2 深度神经网络结构

定义4指数加权平均 指数加权平均是一种近似求平均的方法，应用在很多深度学习[16]的优化算法中，其核心表达式如下：

vt=β·vt-1+(1-β)θt

(5)

式中:t为迭代次数；vt代表到第t次的平均值；θt表示第t次的值；β表示可调节的超参数。通过指数加权平均，各个数值的加权随着t而指数递减，越近的θt的加权越重，第t-1、t-2、…、1次的加权分别为β(1-β)、β2(1-β)、…、βt-1(1-β)。

Adam算法是目前神经网络优化算法中优秀的算法之一，是传统随机梯度下降的优化算法。随机梯度下降在训练时保持单一学习率更新网络参数，学习率在训练过程中不改变，Adam通过计算梯度的一阶和二阶矩估计使得不同参数有独自的自适应学习率。Adam算法在实践中性能优异、相较于其他随机优化算法有很大优势。其伪代码如下：

输入：学习率α(默认为0.001)；矩估计的指数衰减速率β1和β2∈[0,1]，建议分别默认为0.9和0.999；用于数值稳定的小常数δ，默认为10-8；初始参数θ。

输出：θ

初始化一阶和二阶矩变量s=0,r=0

初始化时间步t=0

While没有达到停止准则do

从训练集中采包含m个样本{x(1),x(2),…,x(m)}的小批量，对应目标为y(i)。

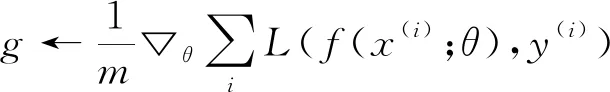
t←t+1

更新有偏一阶矩估计：s←β1s+(1-β1)g

更新有偏二阶矩估计：r←β2r+(1-β2)g·g

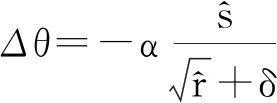
应用更新：θ←θ+Δθ

End while

2 差分隐私下的Adam优化算法

2.1 DP-SGD算法

为了实现神经网络优化算法的隐私保护，Abadi等[7]提出了一种在优化过程中实现差分隐私保护的方法——基于随机梯度下降的差分隐私保护下的优化算法(DP-SGD)。由于从数据的训练到模型的生成完全可以依赖计算梯度的过程实现，因此，该方法通过在随机梯度下降的过程中结合差分隐私理论给梯度添加噪声来实现差分隐私保护。在每一个训练步骤t中，计算具有采样概率L/n的随机样本Lt的梯度并通过l2范数来约束梯度，再给约束后的梯度添加噪声,最后更新参数θt+1。其伪代码如下：

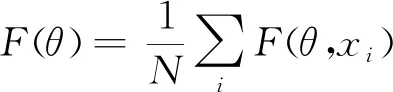
参数：学习率αt,样本容量L,预设的梯度阈值C

随机初始化θ0

fort∈[T] do

选取采样概率L/n的随机样本Lt

/*计算梯度*/

fori∈Lt，计算gt(xi)=▽θtFxi(θt)

/*约束梯度*/

/*加噪声*/

/*更新参数*/

Output:θT

DP-SGD方法通过在随机梯度下降的过程中添加噪声解决了算法在优化过程中的隐私泄漏问题。实验表明：(1) 在适当的隐私预算内，DP-SGD提供了较好的隐私保护水平。(2) Δf/ε越小，模型预测的精度越高，即加入的噪声越小，模型的精度越高。

但是，DP-SGD方法存在一个缺陷，即所添加的噪声对模型精度的影响较大。以图3中的A区域为例，由于每次添加的噪声都是符合某一分布的随机数字，这就导致每一次随机添加的噪声极有可能分布在A区域的两侧。根据DP-SGD的实验结论分析可知，随机噪声尽量地分布在A区域会提高模型的精度。

图3 Laplace分布

2.2 DP-Adam算法

为了实现对神经网络优化算法的隐私保护而提出了差分隐私下的Adam优化算法研究(DP-Adam)。Adam是一种性能优秀的梯度下降算法，将其与差分隐私结合，在神经网络反向传播的Adam梯度下降更新参数过程中加入满足差分隐私的拉普拉斯噪声，从而达到在神经网络优化算法的优化过程中进行隐私保护的目的。相比于DP-SGD方法，该方法在满足同等隐私预算的情况下模型的精度更高，而且在模型达到同样精度要求下所需要的隐私预算更小，即隐私保护程度更高。DP-Adam算法的主要步骤如下：

Step1计算每一次梯度下降时权重和偏置的梯度：

(6)

Step2加入拉普拉斯噪声：

(7)

Step3使用Adam优化方法迭代更新参数：

(8)

(9)

(10)

(11)

(12)

如图3所示，当b=Δf/ε越小时，拉普拉斯噪声分布越集中于A区域(μ=0附近)。DP-SGD[7]的实验结果表明，Δf/ε越小，模型的精度越高，即加入的噪声分布离μ=0越近，模型的精度越高。

对于同一数据集，敏感度Δf是相同的，隐私预算ε决定了训练模型的隐私保护程度和预测结果的准确性，当ε设置相同时，DP-SGD方法在梯度下降第t次更新参数时加入的噪声为：

N=(1-β)Lap(Δf/ε)[t]

(13)

可知，第t次梯度下降参数加入的噪声仅与第t次加入的随机噪声相关，与前t-1次加入的随机噪声无关。根据拉普拉斯概率分布可知，所添加的噪声是满足该拉普拉斯分布的随机数，无法保证添加噪声尽量分布在A区域(μ=0附近)。

DP-Adam算法在梯度下降第t次更新参数时加入的噪声为：

(14)

第t次梯度下降时参数加入的噪声为本次添加的随机噪声和前t-1次加入噪声的指数加权平均。因此，DP-Adam方法加入的噪声由于指数加权平均的限制，很明确地使噪声分布有更大概率分布在A区域(μ=0附近)，也就是在敏感度Δf和隐私预算ε一定的情况下，DP-Adam方法加入的随机噪声参数b=Δf/ε更小。因此，在隐私保护程度相同时，DP-Adam的模型精度更高。DP-Adam算法如下：

参数：步长α(默认为0.001)。随机选取的样本规模L,用于数值稳定的小常数δ,默认为10-8。矩估计的指数衰减速率β1和β2∈[0,1],建议分别默认为0.9和0.999。

输出：θ

随机初始化w、b

初始化一阶和二阶矩变量s=0、r=0

初始化时间步t=0

Whilet∈[T] do

随机选取样本Lt,采样概率为q=L/t

/*计算梯度*/

对于i∈Lt,计算gt(xi)←▽θtL(wt,bt,xi)

/*加噪*/

/*计算加噪后的平均梯度*/

t←t+1

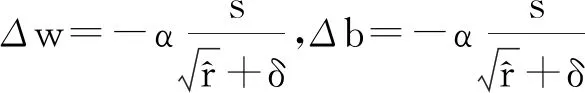
应用更新：w←w+Δw,b←b+Δb

End while

由式(2)和式(4)可知，算法中加入的拉普拉斯噪声的尺度参数b=Δf/ε,在同一个实验中加入的是一个参数确定的拉普拉斯噪声分布，即μ和b是确定的某两个值，同一实验的敏感度Δf也是确定的。因此，在同一实验中ε的值也是确定的，根据b=Δf/ε,我们可以得到ε=Δf/b。

3 实 验

本文选取了机器学习常用的两种用于图片识别的数据集MINIST和CIFAR-10。MNIST数据集包括60 000个样本的手写数字图片训练集和10 000个样本的手写数字图片测试集，其中手写数字图片为28×28像素的灰度图像。CRFAR-10数据集包含10种不同物品分类的彩色图片，训练集有50 000个样本，测试集有10 000个样本。实验对比了DP-Adam方法与文献[7]提出的DP-SGD方法在两种数据集上的结果。

实验环境：CPU为Inter Core I7-7500 3.70 GHz,内存16 GB,GPU为Nvidia GeForce GTX1060(6 GB)。

3.1 MINIST

图4为MNIST数据集在不同隐私预算下的训练模型的精度，ε表示隐私预算的大小、epoch为训练的轮数。如图4(a)所示，ε较小时(即噪声规模较大)两种方法的模型精度均受到噪声影响较大，但DP-Adam方法的模型精度明显更高。随着ε的增大，精度逐渐增加。在训练的稳定时期，DP-Adam的模型精度达到99%,而DP-SGD仅有89%。相同ε下，DP-Adam方法的准确率受到噪声的影响始终小于DP-SGD方法。此外，当两种方法的模型精度相同时，DP-Adam使用的隐私预算明显小于DP-SGD,即DP-Adam的隐私保护性能更好。图4(b)-(d)为三种不同隐私预算下，训练轮数epoch与模型精度的变化关系曲线，可以看出两种方法训练时间接近，但DP-Adam方法精度更高。当训练达到稳定的状态时，DP-Adam算法分别在添加大噪声(ε=0.5)、中等噪声(ε=1)以及小噪声(ε=2)时的模型精度是90%、95%和99%,而DP-SGD算法达到的精度分别是80%、82%和87%。

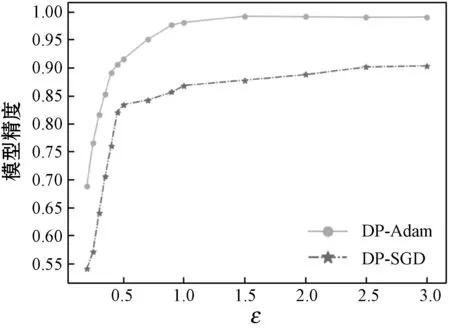
(a) accuracy vs.ε

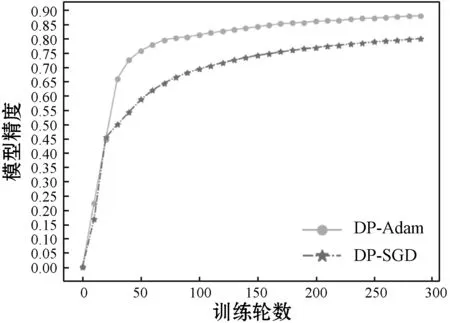
(b) ε=0.5(large noise)

(c) ε=1(middle noise)

(d) ε=2(small noise)

3.2 CIFAR-10

图5为CIFAR-10数据集在不同隐私预算下的训练模型的精度。图5(a)中，随着ε增大(噪声规模减小)，两种方法的模型精度均逐渐上升。在训练的稳定时期，DP-Adam的模型精度达到87%,而DP-SGD仅有75%。在同等噪声规模下，DP-Adam方法的模型精度均高于DP-SGD。此外，当两种方法的模型精度相同时，DP-Adam使用的隐私预算明显小于DP-SGD,即DP-Adam的隐私保护性能更好。图5(b)-(d)为三种不同隐私预算下，训练轮数epoch与模型精度的变化关系曲线，可以看出两种方法训练时间接近，但Adam方法的模型精度更高。当训练达到稳定的状态时，DP-Adam算法分别在添加大噪声(ε=1)、中等噪声(ε=2.5)以及小噪声(ε=6)时的模型精度为73%、78%和88%，而DP-SGD算法达到的精度分别是67%、73%和77%。

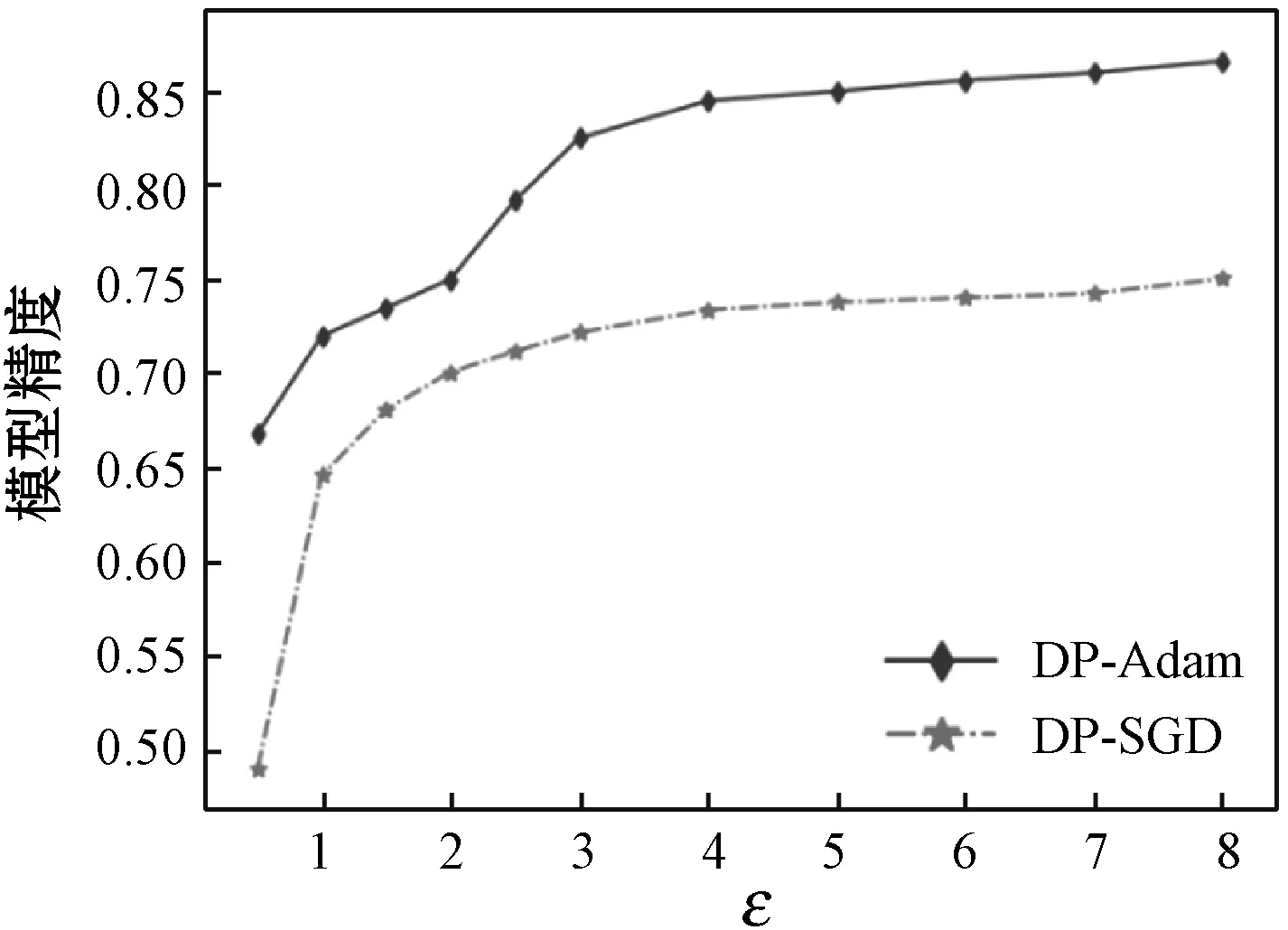
(a) accuracy vs.ε

(b) ε=1(large noise)

(c) ε=2.5(middle noise)

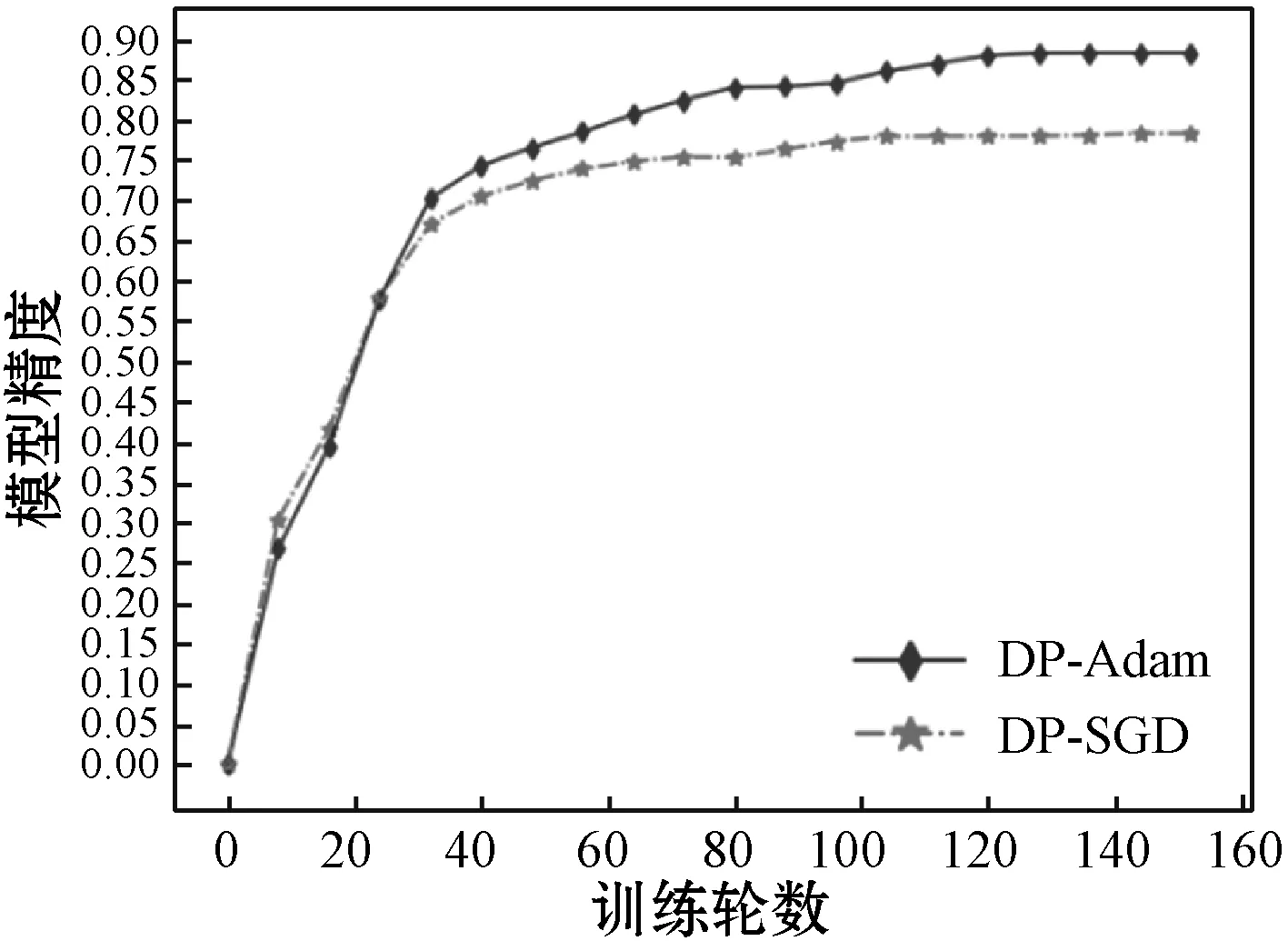
(d) ε=6(small noise)

4 结 语

本文提出了差分隐私保护下的Adam深度学习算法研究。该方法结合差分隐私理论在深度学习训练过程的反向传播时使用Adam优化算法，并且利用Adam算法的指数加权平均思想降低了添加噪声对模型精度的影响。采用Adam优化算法，第t次梯度下降时参数加入的噪声为本次添加的随机噪声和前t-1次加入噪声的指数加权平均，这使得在相同敏感度Δf和隐私预算ε下，DP-Adam方法加入的随机噪声比起DP-SGD方法加入的随机噪声更集中分布在μ=0的区域，进而使得随机噪声的参数b=Δf/ε变小。通过理论与实验得出结论：1) 在同等的隐私保护程度下，DP-Adam方法的模型精度明显高于DP-SGD；2) DP-Adam的隐私保护性能更好。