Fast-ICA算法非线性函数性能的仿真分析
陈秀敏 李珊君* 董兴建
1(四川大学电气信息学院 四川 成都 610065)
2(国网徐州供电公司 江苏 徐州 221000)
0 引 言
盲源分离[1](Blind Source Separation,BSS),或称为盲信号分离的具体过程如下:在信号的数学模型和源信号的具体信息未知时,从得到的已知混合信号求得各路源信号的过程。盲源分离的理想结果是找到最接近源信号的估计值。目前,解决盲分离最受欢迎的方法是独立分量分析(Independent Component Analysis,ICA)[2-4],该方法在语音识别、图像处理和信号分析等方面都得到了普遍的应用。
1991年,文献[5-7]对于盲源分离问题,提出了ICA最原始的概念,至此,盲源分离得到了重大突破。在此期间,Tong等[8]也分析了盲源分离的两大属性:可分离性和不确定性。1994年,Comon[2]系统地分析了盲源分离中关于瞬时混合信号的问题,这一分析精确地解释了独立分量分析理论的形成。Hyvärinen等研究了源信号的非高斯性,提出了一种新的算法:固定点训练算法(fixed-point),并在1997年第一次提出了一种基于峭度的Fast-ICA算法[9]。不久,他又分析了另一种基于负熵的Fast-ICA算法[10]。
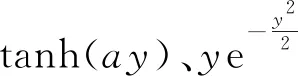
本文分析了基于负熵最大时,采用三种最典型、最常用的非线性函数构造目标函数时,相应Fast-ICA算法的性能比较,并分析总结了这三种非线性函数的图像对比和相似之处。通过仿真实验进行结果分析和误差对比得出结论:当使用非线性函数y3时,算法的分离性能很好,分离精度较高,且它的平均迭代次数最少,收敛速度最快,被证明是最优的函数形式。
1 基于负熵的Fast-ICA算法
Fast-ICA问题的数学模型描述如下:X=AS+n。其中,X=[x1,x2,…,xm]T是观测信号,维度为m,A为将源信号进行混叠的混合矩阵且未知,S为源信号,n=[n1,n2,…,nm]T为噪声。Fast-ICA的目的是在源信号S和混合矩阵A都未知的情况下,仅有观察数据X,通过对X处理得到Z,然后,找到一个分离矩阵W实现从Z中分离出源信号S,表达式为Y=WZ。其中,Y为S的估计值。
1.1 Fast-ICA算法的基本原理
在进行独立信号提取前,必须先找到一种判别准则来衡量分离信号的非高斯性,即独立性。本文判别信号非高斯性的依据是负熵,同时采用非高斯性最大化的估计方法。
微分熵的定义式为:

(1)
式中:f(y)为y的概率密度函数。负熵定义为:
J(y)=H(ygauss)-H(y)
(2)
式中:ygauss与y是两个随机高斯变量,有着相同的方差。根据信息论理论,如果存在相同方差的两个随机变量,具有高斯分布的那个随机变量有着最大的微分熵。当y是高斯分布时,在实际情况中J(y)=0;y的非高斯性越强,则J(y)越大,因此J(y)可以作为衡量随机变量y非高斯性的一个有力的测度。为了简化负熵的表达,在随机变量y的概率密度函数f(y)未知的一般情况下,Hyvärinen给出了如下近似定义方法[12]:
J(y)∝{E{G(y)}-E{G(ygauss)}}2
(3)
F(W)=E{Zg(WTZ)}-αW=0
(4)
式中:g(·)为G(·)的导函数,非线性函数g(·)的选择直接影响着算法的性能和效率,是本文讨论的重点。α为常数值,W0为W的最优值时,α可以近似表示为F(W)的雅可比矩阵J(F(W))。
(5)
牛顿迭代公式为:
(6)
F(W)的雅可比矩阵J(F(W))为:
J(F(W))=E{ZZTg′(WTZ)}-αI
(7)
式中:g′(·)为g(·)的导函数;I为单位矩阵。
由于矩阵Z是白化处理后的结果,故式(7)可简化为:
J(F(W))=E{g′(WTZ)}I-αI
(8)
将α≈E{WTZg(WTZ)}代入公式计算,最终得到Fast-ICA的相似牛顿迭代算法公式为:
(9)
(10)
1.2 Fast-ICA算法步骤
基于负熵的Fast-ICA算法的过程如下:
(1) 对观测信号X进行均值为0的处理,即中心化处理。
(2) 对步骤(1)中心化的信号进行白化处理得到Z。
(3) 选择估计的分量个数n,设置迭代次数i。
(4) 选择一个具有单位范数的初始化向量Wi(可以随机选取)。
(6) 标准化处理Wi。
(7) 判断Wi是否收敛,如果是,则继续算法运行;否则返回步骤(5)。
(8) 令i=i+1,如果i≤n,返回步骤(4);否则,算法结束运行。
2 适合Fast-ICA算法的三种非线性函数
Fast-ICA算法中非线性函数的选取,对于算法的性能和效率以及精度有着较大的影响,当选用不合适的函数代入算法中时,算法不能成功地对信号进行分离,或者得到的分离结果与工程要求的精度相差甚远。式(9)中g(·)函数我们通常选用无记忆非线性函数,工程中常用最经典的三个非线性函数如下:
g1(y)=tanh(ay)
(11)
(12)
g3(y)=y3
(13)
式中:常数a的取值范围一般为[1,2],通常取a=1。
从函数形式上来看,这三个函数存在着共同特性:都是奇函数,关于原点对称;在临近零点范围内的取值变化平稳,接近于0。式(11)、式(12)和式(13)的3种非线性函数形成的波形图如图1所示。

图1 3种非线性函数的波形比较
从三种函数的波形图上,无法直观地看出不同函数对算法的影响比重,接下来通过仿真的方法,对这三种函数算法进行对比和分析,得到直观确切的结论。
3 算法仿真与分析
3.1 性能指标
在Fast-ICA算法中,评价算法分离性能的主要指标通常有相关系数、串音误差(Cross-talk Error)、源信号与分离信号的组合散点图等,本文采用相关系数指标。同时,在得到相同精度的分离结果的情况下,比较其迭代次数,多方面地衡量三种函数算法的性能。

(14)
式中:cov(·)表示方差。
两个信号的相关系数的绝对值越接近于1,则认为信号越接近,算法的分离效果越好。
(2) 迭代次数。指为了逼近想要得到的目标或结果,算法中的公式重复计算的次数。在能够得到理想结果的情况下,算法的迭代次数越少,则运行时间相对越短,收敛速度越快。
3.2 仿真实验
对这三种经典非线性函数的算法性能进行仿真分析。分别将这三种非线性函数代入迭代公式中,组成三个不同的迭代公式算法,并构造出两组不同类型源信号进行实验。
3.2.1仿真实验一
实验中,首先构造源信号:正弦信号s1=2sin(0.02πt),方波信号s2=2square(100t,50),锯齿信号a=linspace(1,-1,25),s3=2[a,a,a,a,a,a,a,a]。为了更加准确地对分离效果进行对比分析,加入一个幅值大于0小于1的随机噪声,作为干扰信号,其中采样频率fs=200 Hz,图2为源信号的波形图。利用一个随机矩阵将各路信号进行混合,得到混合信号即为观测信号,如图3所示。

图2 正弦信号、方波信号、锯齿信号、噪声信号组成的源信号波形图

图3 观察信号波形图

表1 三种非线性函数算法的分离效果
结果越接近于1,表明算法分离后得到的信号和源信号相似度越高,由表1可以看出,采用g1(y)和g3(y)函数具有相近的分离结果,且它们的分离结果比采用g2(y)函数时要更好一些。因此,非线性函数g1(y)和g3(y)的算法的分离性能更佳。
为了更清晰地展示不同非线性函数算法的性能比较,表2给出实验1 000次时不同非线性函数算法的平均迭代次数、最大迭代次数、最小迭代次数。当进行1 000次实验时,得到的图形结果由于密度过高影响视觉效果。为了能够得到更加清晰的图示,进行100次分离实验,图4是进行100次分离实验所得到的迭代次数的分布结果图。

表2 三种非线性函数算法的迭代次数比较

图4 三种非线性函数分别进行100次盲源分离
由表2和图4可以看出,三种非线性函数算法的平均迭代次数有较为明显的区别。其中非线性函数g1(y)的算法的迭代次数最大,且比其他两个非线性函数的迭代次数要大很多,而采用非线性g3(y)时,算法的迭代次数最少,平均只有85.6,比g1(y)函数少了十几倍,说明采用非线性函数g3(y)=y3时算法收敛速度最快。
综合表1、表2和图4的结果,函数g1(y)和g3(y)算法的分离性能更佳,而函数g3(y)的算法收敛速度更快,最终得出采用g3(y)=y3函数的算法各项指标都比较良好,不仅有相对更高的算法精度,而且算法收敛速度更快。
图5为三种函数分别进行盲源分离时的一个分离结果,各路信号的顺序、幅度和相位发生了变化。这是因为除了已知各源信号相互独立外,缺乏其他先验信息,所以分离出的信号才会有不同程度的位移等变化,但这并不影响结果。同时,实验也验证了当给源信号设置不同的幅值时,结论依然成立。

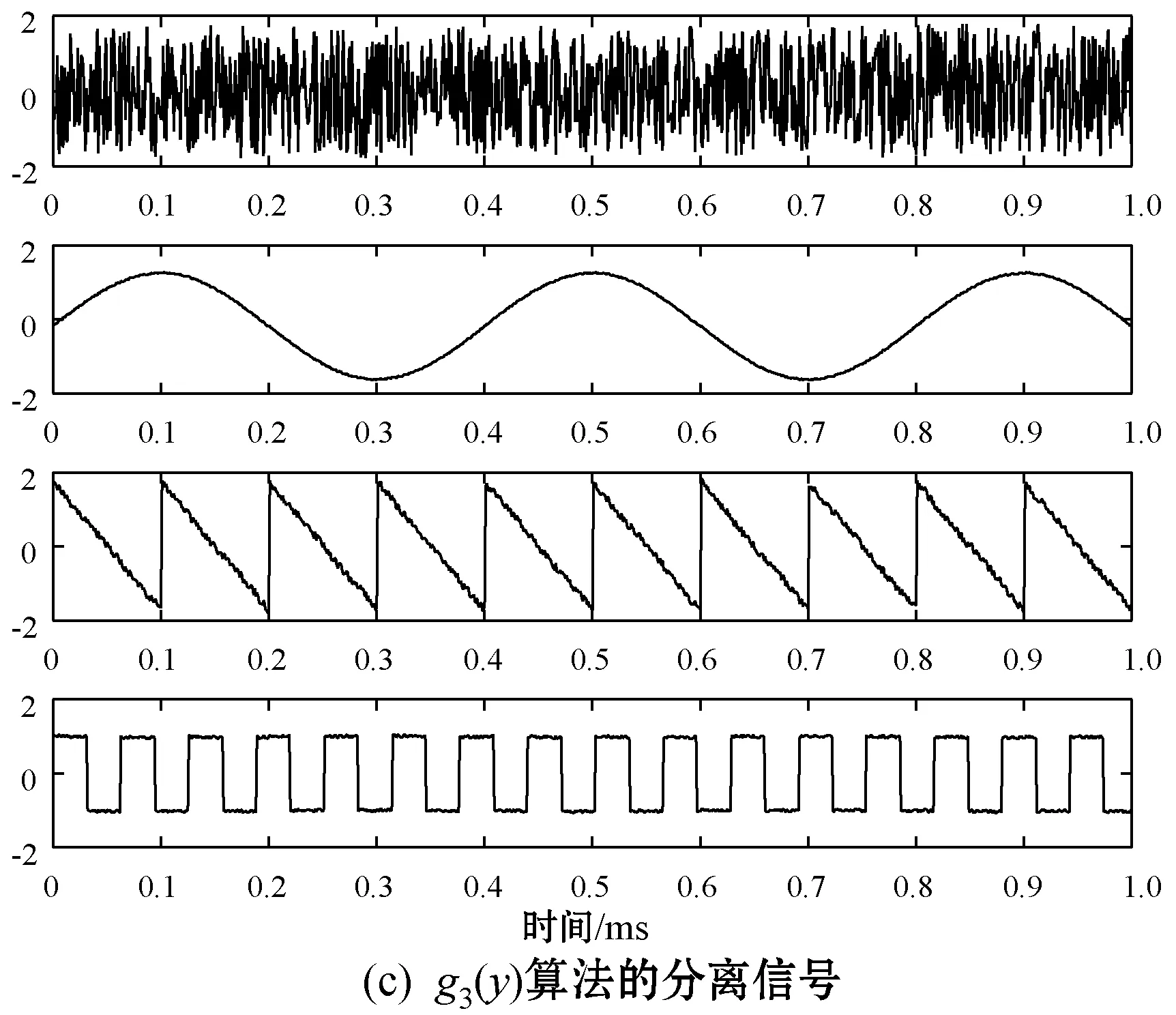
图5 三种非线性函数算法的分离结果
3.2.2仿真实验二
考虑到实验的完备性,为了能够在不同类型的源信号条件下对这三种非线性函数进行分析比较,构造较为复杂的谐波信号作为源信号来进行仿真实验。实验中,构造频率为50 Hz的基波信号以及其3次谐波信号、5次谐波信号,它们的幅值为1,并考虑一个随机噪声,幅值为1,如图6所示。再利用一个随机矩阵将各路信号混合,得到如图7所示的混合信号,即观测信号。

图6 基波信号、3次谐波信号、5次谐波信号、噪声信号组成的源信号波形图
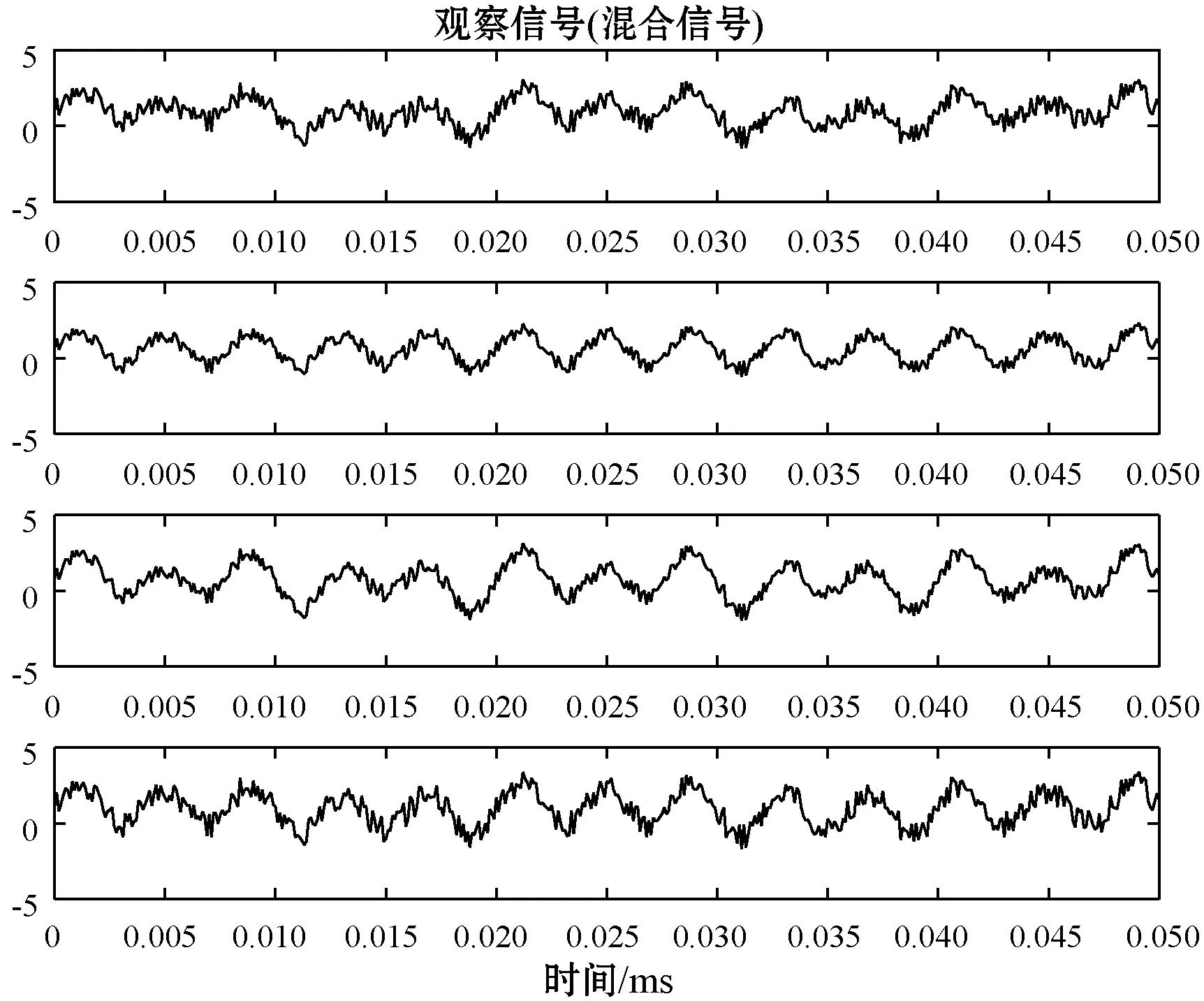
图7 观察信号波形图

表3 三种非线性函数算法的分离效果
可以看出,选用谐波作为源信号时,算法的分离性能没有实验一稳定,谐波有一定的干扰功能,但不影响观察分离结果。相较于g2(y)函数的算法,g1(y)和g3(y)函数的算法分离效果明显更好,因此,g1(y)和g3(y)函数算法的分离性能更佳。
为了更清晰地展示不同非线性函数下算法的性能比较,表4给出实验1 000次时不同非线性函数下算法的平均迭代次数、最大迭代次数和最小迭代次数,图8显示了利用三种非线性函数分别进行100次分离实验所得到的迭代次数的分布结果图。

表4 三种非线性函数算法的迭代次数比较

图8 三种非线性函数分别进行1 000次盲源分离
由表4和图8可以看出,三种非线性函数下算法的迭代次数有明显差别,g1(y)函数的迭代次数最多,g2(y)函数次之,g3(y)函数最少,平均迭代次数只有152.6,且g1(y)和g2(y)函数的迭代次数是g3(y)函数迭代次数的倍数关系,形成非常鲜明的对比。
综合表3、表4和图8的结果,采用非线性函数g1(y)和g3(y)时算法的分离性能更佳,而采用非线性函数g3(y)时算法收敛速度更快,最终得出非线性函数g3(y)=y3的算法的各项指标都比较良好,不仅有相对更高的算法精度,而且算法收敛速度更快。该结论与实验一相似。
图9为三种函数分别进行盲源分离时的一个分离结果,可以看出,当给源信号设置不同的幅值时,结论依然成立。

图9 三种非线性函数算法的分离结果

