基于Cauchy-Schwarz散度的多传感器控制
吴 莎,杨小军
(长安大学 信息工程学院,陕西 西安 710064)
0 引 言
多目标跟踪多传感器技术无论在军事领域还是在民事领域均有广泛的应用,它可用于探测、跟踪和攻击、机器视觉等[1-2]。随着目标的增多,多传感器对于目标的跟踪相较于单传感器有着明显的优势,它对于目标信息的获取有着重大的意义,提高了对目标状态估计的精确性和系统的可信度。由于通信和计算的限制,需要把每个传感器控制在适当的位置,使整个系统达到最优。那么对于诸多传感器采取合适的决策成为必要解决的问题。在大多数目标跟踪场景中,可以通过对传感器的位置、方向等工作方式及参数进行调控而获得不同的量测数据,从而提高传感器检测目标的能力和系统的估计性能,实现整体系统优化。
1997年随机有限集(random finite set,RFS)的提出,避免了多目标跟踪航迹关联的复杂问题,它允许多传感器多目标滤波适应统一的随机集框架进行数据融合[3]。其最大优势是可以将多目标跟踪和传感器控制统一描述为一个贝叶斯框架下部分可观测的马尔可夫决策过程(partially observed Markov decision process,POMDP)[4]。但RFS不能对目标进行唯一标识,进而Vo等学者在2013年提出带标签随机有限集(labeled random finite set,LRFS)的概念,并且提出了广义带标签的多伯努利(generalized labeled Multi-Bernoulli filter,GLMB)滤波器。δ-广义带标签的多伯努利(δ-GLMB)和带标签的多伯努利(LMB)滤波器都是GLMB滤波器的特殊形式,GLMB和δ-GLMB因含有多组分量从而在迭代过程中呈指数形式增长导致计算复杂的问题,而LMB滤波器在定义中只包含一组组件,所以其在迭代过程中的假设分量呈线性增长,有效地解决了GLMB和δ-GLMB计算难的问题。由于LMB滤波器计算效率高,精确地产生目标航迹而得到广泛应用。
多传感器管理是通过优化决策对传感器进行配置。评价函数是产生决策集的重要指标[5],评价函数可大致分为成本函数和回报函数:成本函数主要包括估计目标势方差[6]、势和状态后验期望误差(PEECS)[7]、最优子模式分配(OSPA)距离[8]。成本函数在单目标跟踪中能发挥其性能,但在多目标跟踪中仍有一定挑战。回报函数是基于信息论的,在目标跟踪领域,基于信息论的传感器控制的主要目的是为了通过与目标环境的相互作用以减少目标环境的不确定性,这种不确定性可以用信息熵来定性描述[9]。回报函数最常用一些信息散度,如Rényi散度、Kullback-Leibler(KL)散度和Cauchy-Schwarz(CS)散度。Hoang等人推导出两种泊松点过程混合物的柯西-施瓦茨散度的封闭形式[10],因此与基于信息论的其他散度相比,CS散度在数学计算上更加简单。文献[11]的结果显示CS和KL虽具有相似的计算趋势,但CS的计算要快得多,特别是在维度高的情况下更高效,故选取CS散度作为评价函数对于多传感器管理的研究更为合适。
对于多目标跟踪多传感器控制问题,传感器的管理决策需要信息融合结果的支持,并通过对传感器资源的合理调度来提高信息融合的质量和效率[12]。广义交叉协方差(GCI)被广泛地应用于分布式多传感器多目标跟踪中,但其存在标签不一致的问题。在文献[13-14]中解决此问题的方法是将目标的标签在融合时去掉从而避免标签不一致带来的影响。未带标签的后验密度进行GCI融合确实避免了标签对GCI信息融合的影响,但是因为去掉了标签而不能产生跟踪轨迹,因此文献[15]提出了鲁棒GCI融合(R-GCI),保留后验密度的标签,在不丢失目标轨迹的情况下对信息进行融合但却不会因标签的错误匹配对GCI融合产生影响,通过融合后的密度使传感器的数据得到有效结合,实现了对目标更好的估计[16]。
文中在LMB滤波器框架下,通过选用最优传感器控制决策对目标进行更加精确的跟踪。首先叙述了预备知识:LMB滤波器、Cauchy-Schwarz散度、R-GCI多目标密度融合准则;然后讲述LMB滤波器和CS散度的SMC执行并给出多传感器管理的具体算法步骤;最后通过仿真验证了提出的算法的有效性。
1 预备知识和问题描述
1.1 LMB滤波器
LMB滤波器可以实现目标跟踪的要求,首先,对RFS加入标签将目标的状态扩展为X={(xi,i)}(i=1,2,…,|X|),xi∈,i∈,为目标状态空间,是标签空间,|·|表示目标的势。LMB RFS可以用参数{(r,p(·):∈)}完全表示,这里的r∈[0,1]是目标标签的存在概率,p(·)是目标状态的概率密度函数。LMB RFS密度如下:

(1)
其中:

(2)
(3)
(4)

1.2 柯西-施瓦兹(CS)散度
CS散度是基于内积的柯西-施瓦兹不等式的对称量测距离[18-19],其描述的是两个密度函数f(x)和g(x)之间信息含量的差异性。CS散度的定义如下:
(5)
其中,f(X)和g(X)分别表示目标预测密度和目标后验密度,上式的积分是集积分。
Hong等人在文献[19]中提出泊松点过程的CS散度并证明了两个泊松点过程之间的CS散度是它们各自强度函数之间距离的平方的一半,两个泊松点过程的CS散度的公式表达为:
(6)
其中,G1和G2分别是泊松点过程预测密度和更新密度的强度函数,K表示单目标状态的(超体积)测量单位。上述公式是计算两个带标签多伯努利密度之间的CS散度的基础,在第二部分会给出CS散度的具体计算。
1.3 LMB多目标概率密度的鲁棒GCI融合
Mahler提出次优的广义交叉协方差(generalized covariance intersection,GCI)准则以解决最优融合准则在实际中计算昂贵且公共信息计算难的问题。GCI准则如下:
(7)
其中,ωi是恒定权重,表示在融合过程中强调传感器i的强度。式(7)中的后验密度是未带标签的,文献[15]提出了带标签后验密度的鲁棒GCI融合准则。
文献[15]先定义了多标签的联合条件概率密度:
(8)
带标签的融合后验密度为:
(9)
(10)
(11)
多目标的状态是由N个传感器进行观测,每个传感器返回一组量测值,Zi是第i个传感器返回的量测,量测空间为,设累积的量测集为:
Ik=(Z1,…,ZN)∈
(12)
多传感器控制问题可以转化为部分可观测马尔可夫决策过程(POMDP),POMDP定义为一个6元组:
Ψ={,,f(·|·),,g(·|·),R(u1,…,uN)}
(13)
在控制问题上,目标函数R(u1,…,uN)采用CS散度,CS散度是用预测和后验多目标密度距离之间的关系表示的:
R(u1,…,uN)=DCS(π+,πs,u)
(14)
其中,π+是融合预测密度,πs,u是融合后验密度。最优决策集是通过最大化目标函数的期望值:

(15)
2 基于SMC的多目标多传感器控制问题求解
文献[20]中讨论了三种抵消未来量测不确定性的方法,预测理想量测集(predicted ideal measurement set,PIMS)是其中能更好地产生传感器管理决策的方法。故选用PIMS作为更新步骤中所需的假设量测。对于每个决策ui∈,利用每个状态估计产生无噪声和无杂波的量测,这样的一组量测作为PIMS,用表示:
(16)

2.1 LMB滤波器的SMC执行
多目标后验密度f(X|Z)可以通过一组随机粒子Xj进行近似,每个粒子都有合适的权重。目标的带标签多伯努利密度π={r,p},目标的状态密度p(x)可以用一组粒子集进行近似:
(17)
其中,J是目标采样的粒子数目;ω是每个粒子的权重;δY(X)是狄利克雷函数,当X=Y时等于1,其他等于0。下面介绍LMB滤波器用SMC实现的预测和更新方程。
预测:在这里考虑目标的存活和新生两种,所以LMB预测多目标密度的参数可以表示为:
(18)
其中:
(19)
(20)
ηS()=〈pS(·,),p(·)〉
(21)
更新:传感器i将相应的控制决策u∈和理想量测集应用于滤波器更新,更新的LMB密度为:
(22)
根据文献[22]得出的LMB更新方程,LMB密度的各个参数如下:
(23)
(24)
其中:
(25)
(26)
(27)
(28)
(29)

2.2 基于SMC的R-GCI融合

(30)
将式(29)带入式(13)和式(14)中,用粒子表示融合参数:
(31)
(32)
(33)
2.3 CS散度的SMC实现
结合上面LMB预测和更新方程对CS散度进行SMC执行。预测和更新的LMB强度函数为:
(34)

(35)
对多目标后验分布最有效的近似是多目标分布的一阶矩[22]。文献[9]证明了关于两个多伯努利强度函数的CS散度的公式表达,由此得出两个LMB密度的CS散度公式:
(36)
根据δ函数的积分特性,回报函数为:
(37)
采用逼近之后,问题(15)最优决策的求解为:
(38)
其中,M是采样的粒子数。
综上所述,由于积分计算难的问题,采用SMC逼近融合密度和CS散度以对最优决策进行求解,问题(15)的算法总结如下。
算法1:滤波器迭代、融合和多传感器控制算法。
Step1:根据式(14)~式(17)的预测步进行预测:预测
Step2:计算回报函数:
(1)对于每个粒子X(j)∈T和控制决策(u1,…,uN)∈,计算理想量测集:
(2)根据式(19)~式(25)更新LMB,并保存后验参数和粒子:
(3)对于每个粒子X(j)∈T,每一个控制决策(u1,…,uN)∈的R-GCI融合:
(4)计算每个回报函数:DCS(π+,πu)→R(j)(u1,…,uN)。
求解最优问题(38)是对N个传感器并行求解,这是一个NP难的问题,计算复杂度随着传感器个数的增加而呈指数增加,求解有很大的挑战。而局部迭代搜索[23]是多项式难的问题,在实际中是可行的。故采用局部迭代搜索的方法寻找次优解。
算法2:局部迭代搜索算法。
Step1:选择一组初始决策。



Step2:在初始解的邻域内搜索更好的解。
(3)将余下的传感器重复(1)、(2)的操作,直到所有的传感器都重新选择决策;
(4)对每一个传感器的决策都进行选择,直到穷举完每个传感器的最大决策数,选取使回报函数最大的决策集。
3 仿真分析


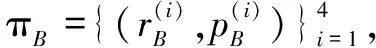
pB=diag([50; 50; 50; 50; 6(pi/180)]T)2。
传感器测量的是具有噪声的极坐标矢量形式:

其中,σD=10 000 m控制检测概率的速率随着范围增大而减小。目标的存活概率pS,k(x)=0.98,单位体积的平均杂波数目λc=12。
传感器平台以8 m/s的恒定速度移动,但在预先指定的决策时间改变航向。每个传感器允许的控制集合是ui=[-1800,-1500,…,00,…,1500,1800],样本数量为M=103,测试场景由三个目标和两个传感器组成,观测时间是60 s,用两个传感器对三个目标进行跟踪,每个传感器每隔10 s做一次决策,10 s内传感器保持当前运动方向不变,每次时间末重新决策,考虑是否改变传感器的运动方向,在仿真时间60 s内,每个传感器共做6次决策。局部滤波器是LMB滤波器,每个节点的GCI融合权重选取0.5。

图1 目标的真实运动轨迹
如图1所示,目标的起始和结束分别用○和△符号表示,每个目标的出生和死亡时间不同,分别在图中标注,图中两个传感器所在位置为初始位置。

图2 传感器运动轨迹
如图2所示,带箭头的线为两个传感器的运动轨迹;由图可看出两个传感器靠近目标运动,可知,提出的控制方法可以做出传感器靠近目标运动的正确决策。
如图3所示,对目标的跟踪性能,局部迭代的搜索法寻找的次优解与穷举法的最优解的性能相近,而随机决策对应的OSPA距离峰值时间滞后且误差大。所以,当传感器数量多且难以计算时,用局部迭代搜索法替代穷举法是可行的。

图3 OSPA距离对比
4 结束语
对多传感器多目标跟踪问题,文中提出一种多传感器最优控制策略。选择CS散度作为系统性能评价函数,通过最大化回报函数实现多个传感器的最优控制。在随机有限集框架下,采用LMB滤波器获得多目标的航迹估计,并且基于保留标签的R-GCI融合准则对多传感器多目标航迹估计进行分布式融合。基于SMC逼近,得到多目标概率密度之间CS散度的数值求解,并且给出基于SMC的LMB滤波器和R-GCI融合地逼近执行。在此基础上提出一种基于局部迭代搜索的传感器控制策略的次优算法。后续工作包括寻找更加有效的多传感器航迹融合方法和优化算法。

