仿生四足机器人步态规划与仿真研究

范向路　曹鹏彬　张毅

摘 要 为了减小仿生四足机器人行走过程中足端冲击力，提高行走稳定性，本文对仿生四足机器人步态规划方面进行了研究，通过分析對比多项式曲线特点，提出了一种多项式组合足端轨迹规划方法，在保证机器人足端在起始点和终点的速度、加速度都为零的条件下，该方法规划的足端轨迹圆滑，同时有效的减小了足端冲击力，实现了机器人足端软着地。采用ADAMS和MATLAB进行对角小跑仿真实验，验证该步态规划算法的合理性和有效性。

关键词 仿生四足机器人 步态规划 对角小跑 仿真

中图分类号：TP242文献标识码：A

0引言

合理的步态规划不仅可以提高仿生四足机器人运动速度、同时也可以减小足端着地时的冲击力，提高机器人运动的稳定性。仿生四足机器人步态规划包含两个方面：一是对仿生四足机器人足端运动轨迹规划;二是对仿生四足机器人各个腿运动时序的规划。

对于机器人足端运动轨迹规划，常见的足端轨迹有摆线、抛物线及多项式曲线等。复合摆线足端轨迹是由Y.Sakakibara提出的，该方法实现了机器人在抬腿和触地时速度和加速度都为零的运动规划，有效地减小的机器人足端触地时的冲击力。东北大学柳洪义采用组合摆线作为足端轨迹，解决了抬腿时急动问题。华中科技大学程品等人对机器人足端摆动相采用五次多项式曲线，该曲线完全满足机器人足端轨迹规划要求，可以使仿生四足机器人实现连续的、稳定的行走。

仿生四足机器人各腿运动时序根据机器人各腿运动占空比 的不同，将仿生四足机器人运动步态分为静步态和动步态。即当0.75≤ <1时，则为静步态;当0.5< <0.75时，则为准动步态;当0< <0.5时，则为动步态。静步态中特指walk（步行）步态，动步态主要包括tort（对角小跑）步态、pace（单侧小跑）步态、gallop（疾驰）步态。

本文通过分析对比多项式曲线特点，提出了一种多项式组合的足端轨迹规划方法，同时根据仿生四足机器人运动稳定性原理，规划了对角小跑步态，最后采用ADAMS和MATLAB进行联合仿真分析，验证此次四足机器人步态规划的正确性和合理性。

1运动学建模与分析

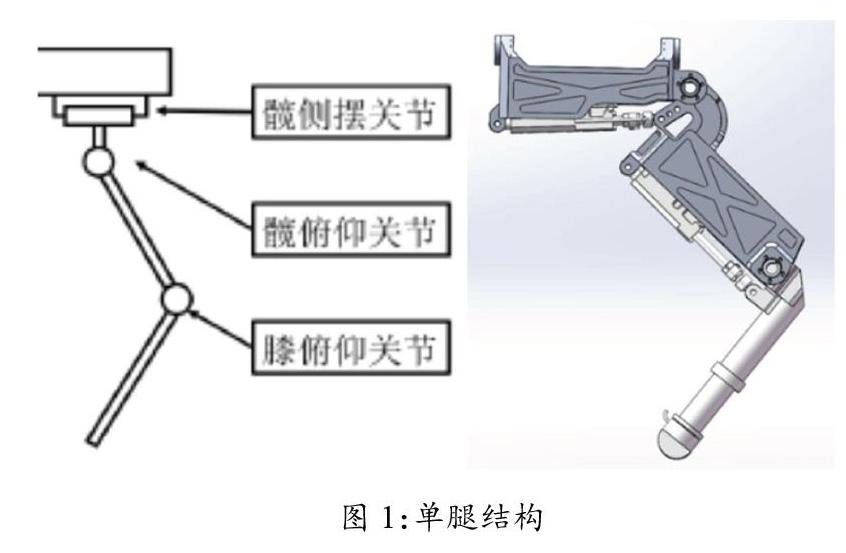
此次设计的仿生四足机器人采用前膝后肘式结构，该结构下的四足机器人机体呈重心对称，在对角小跑等步态中可以减小腿部惯性影响，有利于提高机器人运动稳定性;同时该结构下前后腿之间空间较大，避免前后腿运动关节碰撞，具备较大的摆动范围。仿生四足单腿由三个连杆组成，类似于一个串联的三连杆机构。每条腿有三个转动自由度，分别为髋关节（侧摆和俯仰自由度）、膝关节（俯仰自由度），单腿结构如图1所示。

根据上图单腿结构建立D-H坐标系，选择机体与髋连接点为坐标系原点{1O0}，前进方向为Z轴正方向，重力反方向为X轴正方向，Y方向由右手原则确定。坐标系{1O1}方向与坐标系{1O0}重合，坐标系{1O2}和坐标系{1O3}的Z轴垂直纸面向外，X轴为连杆方向，指向下一个关节，Y轴由右手定则确定，坐标系{1O4}与坐标系{1O3}方向一样，如图2所示。

令足端在基坐标系下的坐标为（px，pv，pz），根据文献[4]可得四足机器人单腿运动学逆解表达式如下：

2仿生四足机器人步态规划

2.1足端轨迹规划

多项式曲线足端轨迹是一个满足足端运动约束条件的多项式表达式：

多项式的阶数取决于运动约束条件的个数，为了使足端轨迹对称，通常取奇数，无特殊轨迹要求时运动约束条件选择在初始时刻和终点时刻。

令步长S=120mm，抬腿高度H=40mm，足端完成一次支撑点转移时间T0=0.5s。对机器人足端摆动相抬腿方向分别采用三次、五次和七次多项式进行轨迹规划分析。根据多项式的阶数，三次多项式约束条件为位置值和速度值;五次多项式约束条件为位置值、速度值和加速度值;七次多项式约束条件为位置值、速度值、加速度值和加加速度值。各多项式轨迹规划的足端在抬腿X方向位置曲线、速度曲线、加速度曲线如图3所示。

对于仿生四足机器人足端轨迹规划为减小冲击力一般要求抬腿时刻和着地时刻速度和加速度为零，在理论上可以减小足端冲击力，但是由于足端具有一定形状或者地面会有凸起，规划的足端轨迹会使足端提前触地，所以这就要求在抬腿时刻和着地时刻附近加速度要尽量小。由上图分析可得多项式阶数越高，在起始位置和终点位置附近速度和加速度较小，当足端在抬腿初期和着地前期可以起到缓冲作用，到达减小足端冲击力的目的;多项式阶数越小，运动曲线的速度峰值和加速度峰值越小，且运动过程中速度变化较为平缓。同时三次多项式不满足初始时刻和终点时刻加速度为零的约束条件，会引起运动突变，所以机器人足端轨迹规划一般不采用三次多项式。综合以上分析，为了减小仿生四足机器人足端触地时的冲击力，同时保证行走过程中运动速度平稳，所以机器人足端轨迹采用多项式组合的方式进行规划：在前进方向运动轨迹采用五次多项式;在抬腿方向运动轨迹采用七次多项式。则仿生四足机器人足端轨迹方程如下：

2.2对角小跑步态规划

对角小跑步态是处于对角线的两条腿具有相同的运动相位，即对角线上的两条腿同时处于支撑相或摆动相。为了防止仿生四足机器人运动发生侧翻，采用零力矩点动态稳定性判据规划对角小跑步态，使机器人在运动过程中ZMP点尽可能的落在支撑足对角线上。根据模型尺寸及运动参数计算处理论重心位置，采用配重法改变机体重心位置，使机器人在运动过中ZMP点尽可能靠近支撑足对角线，以保证机器人运动的稳定性。

此处规划选择占空比 =0.5，当摆动腿着地的同时，另外两条腿立即抬起来，运动过程如图4所示，图中红点为机体重心位置，黑点为支撑腿、白点为摆动腿。摆动腿相对机体向前摆动，同时支撑腿推动机体向前运动，调整机体重心位置。

3仿生四足机器人仿真

为了验证此次步態规划的合理性，采用ADAMS和MATLAB进行联合仿真分析。对角小跑步态仿真参数设定：步态周期T=0.8s，单腿跨距S=112mm，摆动相抬腿高度H=40mm，仿真时间t=16s。机体质心位置变化曲线如图5所示。

仿生四足机器人20个步态周期行走了4558mm，理论行走位移是4592mm（20个步态周期和一次质心调整112mm），主要是因为机器人支撑腿在推动机体向前运动时足端与地面存在相对滑动，所以产生了位移误差，误差比为前进方向的0.7%左右;机体质心在竖直方向的波动曲线最大值为1.5mm，最小值为-4mm，在正常波动范围内，且呈规律性变化，可认为四足机器人运动较为平稳。

图6为对角小跑步态左后腿足端接触力曲线，左侧是采用多项式组合规划足端轨迹的足端接触力曲线，右侧是采用五次多项式规划足端轨迹的足端接触力曲线，通过对比发现左侧接触力无论是在峰值还是均值都比右侧小，起到了减小足端冲击力的效果。

4结论

本文提出了一种多项式组合的足端轨迹规划方法，该方法不仅满足仿生四足机器人足端轨迹规划要求，同时该方法相比与其他方法，有效的减小了机器人足端冲击力，并根据零力矩点动态稳定性判据规划了对角小跑步态。最后采用ADAMS和MATLAB进行联合仿真实验，验证了此次四足机器人步态规划的正确性和合理性。

*通讯作者：曹鹏彬

参考文献

[1] Yoshihlro Sakakibara， Kazutoshi Kan， Yuuji Hosoda， et al. Foot trajectory for a quadruped walking machine [C] IEEE International Workshop on Intelligent Robots and Systems， IROS，1990（01）： 315-322.

[2] 柳洪义，宋伟刚，彭兆行.控制步行机足运动的一种方法工科——修正组合摆线法[J].机器人，1994（06）：350-356.

[3] 程品，罗欣，顾瀚戈.四足机器人砂砾地面对角行走控制方法[J].装备制造技术，2014（04）：8-12.

[4] 朱雅光.基于阻抗控制的多足步行机器人腿部柔顺控制研究[D].杭州：浙江大学，2014.

[5] 赵彦.基于ADAMS和MATLAB的四足机器人联合仿真[D].济南：山东大学，2014.