高压短脉冲作用下HNS-Ⅳ型炸药的全发火冲击起爆判据
王万军,祝明水,郭 菲,吕军军,杨 爽,付秋菠
(中国工程物理研究院化工材料研究所,四川 绵阳 621999)
1 引言
HNS 炸药具有良好的安全性、热安定性和短脉冲冲击起爆性能,广泛应用于冲击片雷管、激光火工品的起爆传爆序列中[1],研究其高压短脉冲起爆特性具有重要意义。不同颗粒度(比表面积)、不同密度HNS 炸药的短脉冲起爆性能明显不同,有必要研究特定颗粒度和特定密度HNS 炸药的起爆判据。经典的p2τ 判据(通常用作pnτ),建立了界面压力p 和持续时间τ 之间需要满足的函数关系[2],获得了广泛应用[3-7];Schwarz等[8]采用电爆炸驱动不同厚度的聚酰亚胺飞片撞击炸药,通过数据拟合确定了对于密度为1.6 g·cm-3的HNS-SF 炸 药,其pnτ 判 据 中 的 指 数n=2.4;James[9]从能量角度出发,进一步提出了炸药的James 冲击起爆判据,获得了较为广泛的应用[10-12];Bowden 等[13]采用激光驱动金属飞片撞击炸药,对HNS 在更高压力(20~30 GPa)和更短脉冲(0.7~1.25 ns)作用下的冲击起爆行为进行了研究,结合Schwarz[8]的实验结果,将pnτ 判据中的n 修正为2.52;Tarver 等[14]在综合了不同粒度的HNS 冲击起爆实验数据的基础上,给出了一套平均的HNS 炸药点火增长模型参数,用于高压短脉冲刺激下HNS 冲击起爆过程的数值计算。国内郭俊峰等[1]基于Schwarz 和Bowden 的实验数据,重新对pnτ判据进行了拟合,并基于数值模拟结果对国产HNS 的起爆判据进行了修正;此外,钱石川等[15]基于文献中的实验数据也对HNS 的冲击起爆判据进行了研究。
国内外研究成果对于HNS-Ⅳ型炸药的冲击起爆特性研究提供了借鉴,上述研究中多采用临界起爆飞片速度来计算撞击压力和持续时间,对应地获得了临界起爆判据,然而,实际工程应用中通常要求HNS-Ⅳ炸药能够可靠的全部起爆,因此有必要研究HNS-Ⅳ型炸药的全发火起爆判据,以期对冲击片雷管等火工品的科学设计提供参考。
常用的高速飞片驱动技术有EFIs 技术[16]、激光驱动飞片技术[17]以及磁压缩驱动技术[18]等,本研究选取目前炸药起爆中应用最广泛的EFIs 技术。首先开展升降法发火试验,获得三种厚度(12.5,40 μm 和50 μm)聚酰亚胺飞片的最小全发火电压,采用PDV 获得对应的撞击速度;通过飞片撞击LiF 窗口的界面粒子速度波形,研究飞片在撞击瞬间的实际厚度;开展理论分析和数值仿真,计算飞片在最小全发火条件下撞击HNS-Ⅳ炸药的界面压力、界面粒子速度和持续时间,通过数据拟合确定HNS-Ⅳ炸药的全发火Pnτ 起爆判据参数。
2 试验研究
2.1 最小全发火条件下的撞击速度
采用升降法确定最小全发火条件。升降法能够用于确定炸药的最小全发火起爆条件[19],样品示意图如图1 所示。由陶瓷塞、爆炸箔、聚酰亚胺、加速膛、HNS-Ⅳ药柱和壳体组成。爆炸箔两端通过金属脚线外接储能电容,电容放电时,爆炸箔中间窄桥在焦耳热沉积下转化为高温高压产物,驱动聚酰亚胺在加速膛内径处剪切形成飞片[20],并在加速膛中持续加速后撞击HNS-Ⅳ药柱将其起爆。调整充电电压进行发火试验,根据GJB376-1987(火工品可靠性评估方法)和GJB377-1987(感度试验用升降法)计算最小全发火电压。

图1 升降法试验样品示意图Fig.1 Schematic diagram of the detonator for up-down methods
采用PDV 测速技术,对三种飞片在对应最小全发火条件下的速度-时间曲线进行测试。测速样品示意图如图2 所示,由陶瓷塞、爆炸箔、聚酰亚胺、加速膛、光纤探头、光纤和壳体组成。测试系统如图3 所示,由测试样品、储能电容、固态开关、信号发生器、PDV 测速仪、示波器、光纤和导线等组成。信号发生器发送两路触发信号,其中一路将固态开关闭合,爆炸箔桥区爆发后驱动飞片加速;另一路触发信号触发示波器,开始记录PDV 测速仪发送的激光信号,对激光信号进行处理即可获得飞片的速度-时间曲线,如图4 所示。
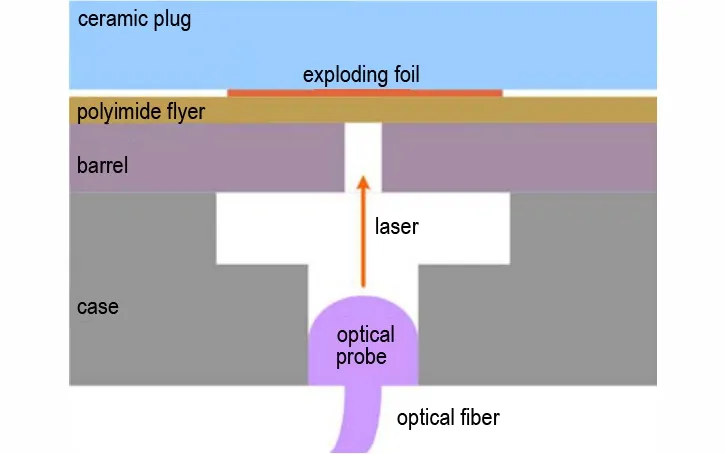
图2 飞片撞击速度测试样品示意图Fig.2 Diagram of the sample for impact velocity measurement
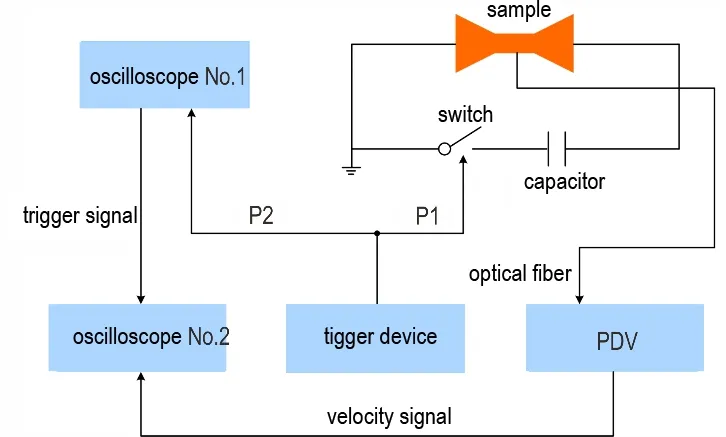
图3 PDV 测速系统示意图Fig.3 Diagram of PDV system
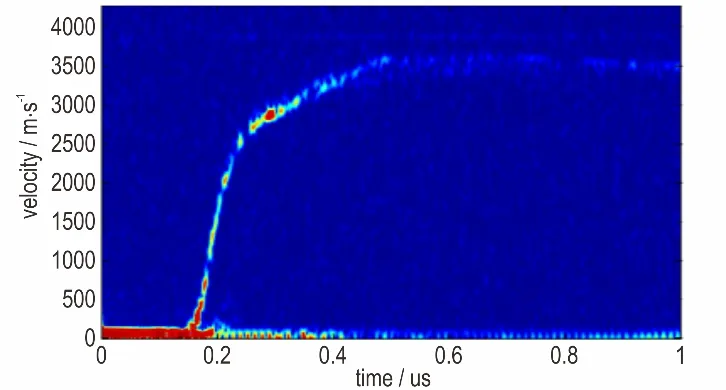
图4 典型的飞片速度-时间曲线Fig.4 Typical flyer velocity history captured by PDV
三种厚度的飞片在最小全发火条件下的速度-时间曲线以及积分获得的位移-时间曲线如图5 所示。通过速度-时间曲线和位移-时间曲线的对比,获得三种厚度的飞片在加速膛出口处的速度(即撞击速度)分别为3400,3100 m·s-1和2930 m·s-1。
2.2 撞击瞬间飞片厚度
Bowden[13]提出,飞片在加速过程中可能变薄,导致脉冲压力的持续时间变短。对于EFIs 驱动的飞片,虽然爆炸产物的温度远高于飞片的热分解温度,但是飞片与爆炸产物的接触时间仅为亚微秒尺度,这两方面的竞争关系使飞片撞击炸药瞬间的厚度很难确定。本研究将飞片撞击窗口的界面粒子速度波形与仿真结果对比,确定飞片撞击窗口瞬间的实际厚度。
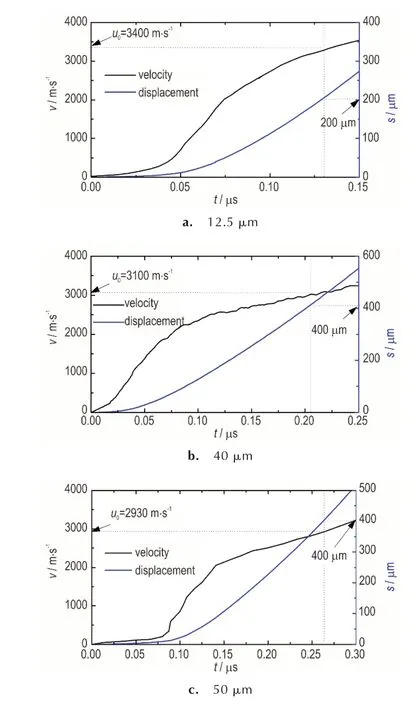
图5 三种厚度的飞片在最小全发火条件下的速度-时间曲线和位移时间曲线Fig.5 Velocity and displacement history of three different thickness flyers under their minimum all-fire charging voltages
采用PDV 测试飞片撞击LiF 窗口的界面粒子速度,测试样品示意图如图6 所示,由陶瓷塞、爆炸箔、聚酰亚胺、加速膛、LiF 窗口、光纤探头、光纤和壳体组成。LiF 窗口的上表面镀有0.2 μm 厚的铝反射膜,作为界面粒子速度的载体。数值计算模型如图7 所示,计算模型中飞片厚度为其初始厚度,飞片和LiF 窗口均采用Lagarange 网格建模,设置Lagrange/Lagrange Interaction 描述飞片和窗口的碰撞作用。聚酰亚胺和LiF均采用Shock 状态方程,状态方程参数见表1。
采用图7 所示的计算模型,选用厚度为40 μm 的飞片进行网格收敛性验证。网格尺寸为8,4,2 μm 和1 μm 时的界面粒子速度对比见图8。由图8 可以看出,网格尺寸为2 μm 和1 μm 时的计算结果已经非常接近,计算结果基本收敛,下文均采用1 μm 的网格进行计算。
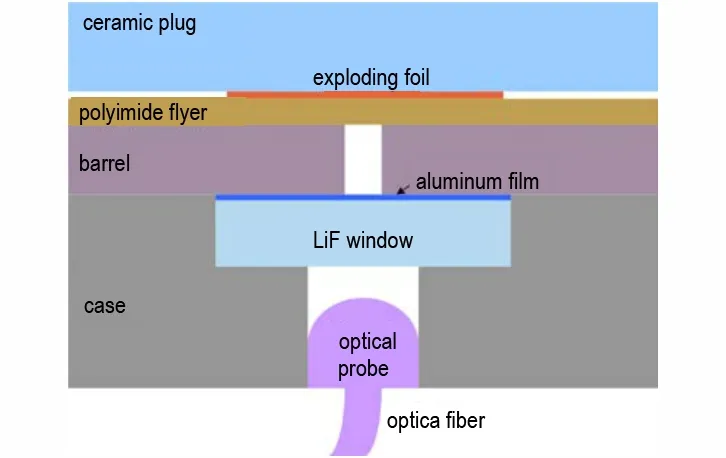
图6 界面粒子速度测试用样品示意图Fig.6 Diagram of the sample for the measurement of interface particle velocity

图7 LiF 飞片撞击LiF 窗口计算模型Fig.7 Simulation model of flyer impacting onto LiF window

表1 聚酰亚胺和LiF 的Shock 状态方程参数Table 1 Parameters of Shock EOS for polyimide and LiF
界面粒子速度波形的PDV 测试结果与仿真结果对比见图9。厚度为12.5 μm 的飞片,其计算结果与PDV 测试结果几乎完全一致,表明飞片在撞击窗口瞬间厚度仍为12.5 μm。对于厚度为40 μm 和50 μm的飞片,PDV 测试波形的脉宽明显小于计算结果,表明飞片在撞击窗口时厚度有所减小。将计算模型中飞片厚度分别设置为21 μm 和25 μm 后,计算界面粒子速度波形与PDV 测试结果基本重合,表明厚度为40 μm 和50 μm 的飞片在撞击窗口时的实际厚度减小为21 μm 和25 μm。后续将采用飞片撞击窗口时的实际厚度计算脉宽。

图8 不同网格尺寸下的界面粒子速度历程Fig.8 Interface particle velocity history by simulation with different mesh size
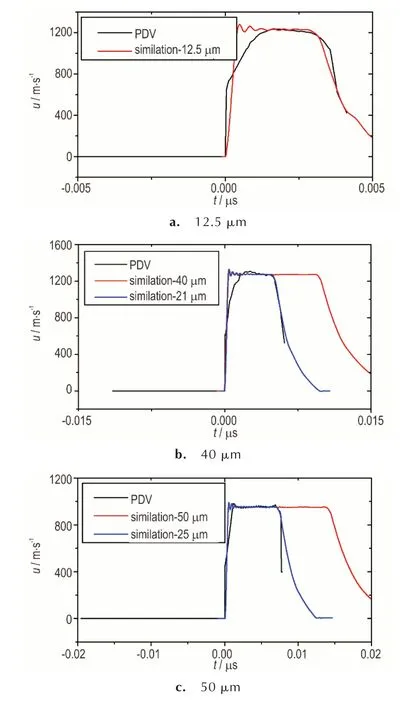
图9 三种厚度飞片测试界面粒子速度与仿真结果对比Fig.9 Comparison of particle velocity history by PDV and simulation
3 撞击参数计算
3.1 界面粒子速度
假设飞片材料的Hugoniot D-u 关系和HNS-Ⅳ炸药的未反应Hugoniot D-u 关系满足线性规律,界面粒子速度u 可通过求解方程(1)获得:

式中,ρe和ρp分别为HNS-Ⅳ和聚酰亚胺的初始密度,g·cm-3;C0e和C0p为声速,m·s-1;λe和λp为冲击Hugoniot D-u 曲线的斜率;u0为飞片撞击速度,m·s-1。聚酰亚胺的材料参数见表1,HNS-Ⅳ型炸药的密度为ρe=1.56 g·cm-3,未反应Hugoniot 参数通过反撞法火炮试验确定为:C0e=1396 m·s-1,λe=2.215。计算所得界面粒子速度u 见表2。

表2 三种厚度的飞片在最小全发火条件下撞击HNS-Ⅳ炸药的脉冲压力参数Table 2 Parameters of the transimition wave in HNS-Ⅳbooster impact by flyer with 3 different thickness
3.2 界面压力
获得界面粒子速度u 后,界面压力p 可通过式(2)计算:
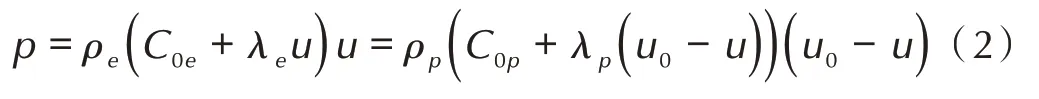
界面压力的计算结果见表2。由表2 可知,对于三种不同厚度的飞片,其最小全发火条件下的压力幅值相差并不大:当厚度为12.5 μm 时,撞击界面压力为13.0 GPa;当 厚 度 为25 μm 时,撞 击 界 面 压 力 为10.3 GPa。虽然厚度增加了一倍,但是其界面压力仅仅减小了20.8%,暗示从飞片动能角度考虑,理论上较薄的飞片需要更小的动能就能够使得HNS-Ⅳ炸药获得接近100%的发火概率。
3.3 持续时间
当飞片的直径和厚度比较大时,冲击波从撞击面传播至飞片背面并再次返回撞击面的时间非常短,可以忽略飞片边界效应对界面压力持续时间的影响,从而近似认为撞击过程是一维的,采用式(3)估算界面压力的持续时间τ:

式中,h1为撞击瞬间飞片厚度,μm;D 为飞片中冲击波相对于波前介质的传播速度,m·s-1。D 通过式(4)计算:

根据式(4)计算所得持续时间如表2 中的τ1所示。式(3)假设了冲击波从飞片正面(撞击面)到飞片背面的传播时间,与稀疏波从飞片背面返回正面的时间相同。实际上,稀疏波返回的时间明显更小,这主要是由于撞击瞬间,飞片正面的质点速度由u0瞬间下降为u,而此时飞片背面尚未受到影响,速度仍为u0,因此在冲击波从飞片正面传播至背面的时间段h1/D 内,背面的运动速度始终大于正面,速度差为u0-u,导致这段时间内飞片厚度不断变薄,因此稀疏波返回时的传播距离由h1减小为h1-(u0-u)(h1/D)。假设稀疏波返回时相对于波前介质的传播速度与冲击波相同,则界面压力的持续时间应由式(3)修正为:

根据式(5)计算所得持续时间如表2 中的τ2所示。可以看到,修正后的持续时间τ2要明显小于修正前的τ1,偏差大约为15%~20%。为了进一步验证式(5)的计算结果,采用AUTODYN 对飞片撞击HNS-Ⅳ过程进行数值仿真,仿真所得持续时间记为τ3。可以看出,仿真结果与式(5)的计算结果基本一致,表明在一维冲击条件下,界面压力的持续时间由式(5)进行计算更加准确。下文也将采用修正后的持续时间τ2进行起爆判据的拟合。
4 判据拟合
常用的炸药冲击起爆判据有pnτ 判据,如式(6)所示。

式中,p 为界面压力,GPa;τ 为脉冲压力的持续时间,μs;n 和K 为待拟合的参数。作为一种拟合式判据,该判据认为界面压力和持续时间是起爆的决定因素,本研究假设炸药的全发火起爆特性也是由这两个参数决定的,因此也可以采用pnτ≥K 的方程形式表征其全发火起爆特性。
结合表2 中的数据,对式(6)中的常数n 和K 进行拟合,拟合所得pnτ 判据为:p2.88τ≥7.21,拟合结果的决定因子R2为0.9988,拟合判据与试验结果的对比如图10 所示。本研究拟合所得指数n 相较文献[8,13]中的数值偏大,这可能是由于HNS-Ⅳ型炸药的全发火起爆特性和临界起爆特性不同引起的。还需要说明,在不同的撞击压力区间内,炸药的起爆判据也会有所不同,因此本研究获得的全发火起爆判据,仅在其覆盖的压力区间内适用。
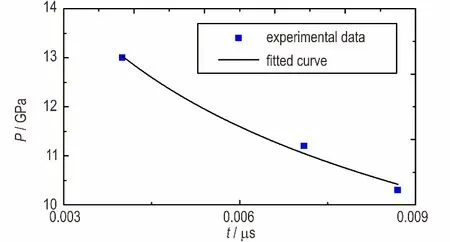
图10 起爆判据的拟合结果与试验数据的对比Fig.10 Comparison between the fitted criterion and experimental data
5 结论
(1)通过升降法试验和PDV 测速技术,获得了不同厚度飞片在最小全发火条件下的撞击速度,当飞片厚度为12.5,40 μm 和50 μm 时,最小全发火撞击速度分别为3400,3100 m·s-1和2930 m·s-1;
(2)将PDV 测试所得LiF 窗口的界面粒子速度波形与数值仿真结果对比,表明聚酰亚胺飞片在加速过程中厚度可能会减小;
(3)聚酰亚胺飞片撞击HNS-Ⅳ炸药的脉冲压力持续时间小于2h1/D,需要考虑飞片在冲击波压缩后的厚度变化进行修正;
(4)通过数据拟合,获得HNS-Ⅳ炸药的全发火pnτ 判据为:p2.88τ≥7.21,该判据适用于本研究所研究的炸药和压力范围,研究结果对于冲击片雷管等火工品的设计具有一定的指导意义。

