HTPB 推进剂三点弯曲过程试验与数值模拟
伍 鹏,李高春,王 鑫
(1. 海军航空大学 研究生大队,山东 烟台 264001;2. 海军航空大学 导弹总体与发动机教研室,山东 烟台 264001)
1 引言
端羟基聚丁二烯(HTPB)推进剂广泛应用于各类固体火箭发动机,发动机中推进剂药柱的形状复杂,在机械载荷的作用下,在某些关键部位产生损伤从而萌生裂纹。裂纹的产生导致发动机的燃面增大,进而影响发动机工作过程[1-2],因此对推进剂裂纹的研究一直是人们关注的重点。张亚[3]研究了某型复合固体推进剂在Ⅰ-Ⅱ复合型裂纹下的断裂行为,得到了不同裂纹倾斜角下裂纹扩展开裂角和断裂载荷。龙兵[4]研究了高应变率下HTPB 推进剂的断裂性能,发现推进剂的动态起裂韧性具有明显的应变率敏感性,应变率越高,越表现为脆性断裂特征。汪文强[5]研究了冲击载荷下CMDB 裂纹尖端的损伤过程,获得了推进剂的Ⅰ型动态起裂韧性,并建立了数值模型,模拟了推进剂静态加载下的裂纹扩展过程,发现裂纹首先呈Ⅰ型扩展,最后以复合断裂形式扩展失效。韩波[6]建立了HTPB 推进剂的粘聚区本构,对推进剂断裂过程进行了数值模拟,较好地还原了推进剂Ⅰ-Ⅱ型裂纹扩展过程。职世君[7]以J 积分作为裂纹扩展起始判据,研究了不同裂纹扩展方向准则对复合型裂纹的扩展过程的影响,发现考虑裂尖构形的影响可以更精确地模拟裂纹初始扩展角度。上述文献对裂纹的研究多是从宏观角度进行的,材料在宏观尺度上的力学表现都是由细观尺度行为演化而成的[8],从细观尺度研究推进剂损伤过程,可以更好地理解推进剂的宏观失效机理。因此,近年来不少学者开始从细观角度对推进剂损伤过程进行研究。李高春[9]研究了不同温度和拉伸速率下复合固体推进剂断面形貌,分析了其破坏模式。Liu[10]的研究表明,推进剂裂纹损伤过程表现为钝化-扩展循环过程。王阳等[11]利用数字图像相关方法分析了HTPB 推进剂三点弯曲裂纹尖端细观形貌演化过程,但是由于裂纹尖端变形较大,数字图像相关无法很好地匹配,尚需进一步研究。
从上述文献研究的特点来看,主要可以分为两个方面:一是通过建立含推进剂裂纹的宏观模型,对裂纹扩展过程进行宏观数值模拟;二是对推进剂裂纹进行损伤试验,采用扫描电镜对推进剂的断面进行观察,获得推进剂断面的细观形貌。对裂纹进行宏观尺度的数值模拟无法揭示裂纹尖端的细观损伤过程,对推进剂断面细观形貌观察无法反映裂纹尖端在宏观载荷作用下的动态损伤过程。因此,本研究结合动态观察试验,建立HTPB 推进剂裂纹尖端动态损伤过程数值模型,从试验和数值模拟两个方面,进一步揭示推进剂裂纹尖端细观损伤机理。
2 细观动态观察试验
2.1 试验方法与过程
试验采用的是某型HTPB 推进剂,其中固体颗粒的质量分数为86%,固体颗粒中AP 含量为69%,铝粉含量为17%,HTPB 基体为11.5%,其他助剂为2.5%。由于扫描电镜的电镜室尺寸限制,不能制作标准三点弯曲试件,只能制作小试件,设计的试件尺寸为30 mm×10 mm×5 mm。为了更好地观察裂纹尖端变化过程,试验之前,用锋利的小刀在试件中央切割一条长度为5 mm 的预制裂纹。试验在岛津JSM-5410LV型SEM 试验系统上进行。通过伺服控制系统控制试验过程的压缩速度,采用SEM 观察试件表面形貌,试验时温度为25 ℃。为了排除试件制作时颗粒残留在试件表面造成的干扰,试验时先将试件表面吹除干净。由于SEM 成像较慢,要求压缩速率不能太快,所以设置压缩速率0.12 mm·min-1。对电镜加载15 kV 电压,设置放大倍数50 倍,调节对比度与亮度,使屏幕能清晰显示裂纹尖端的细观形貌,试件及夹具的安装如图1 所示。
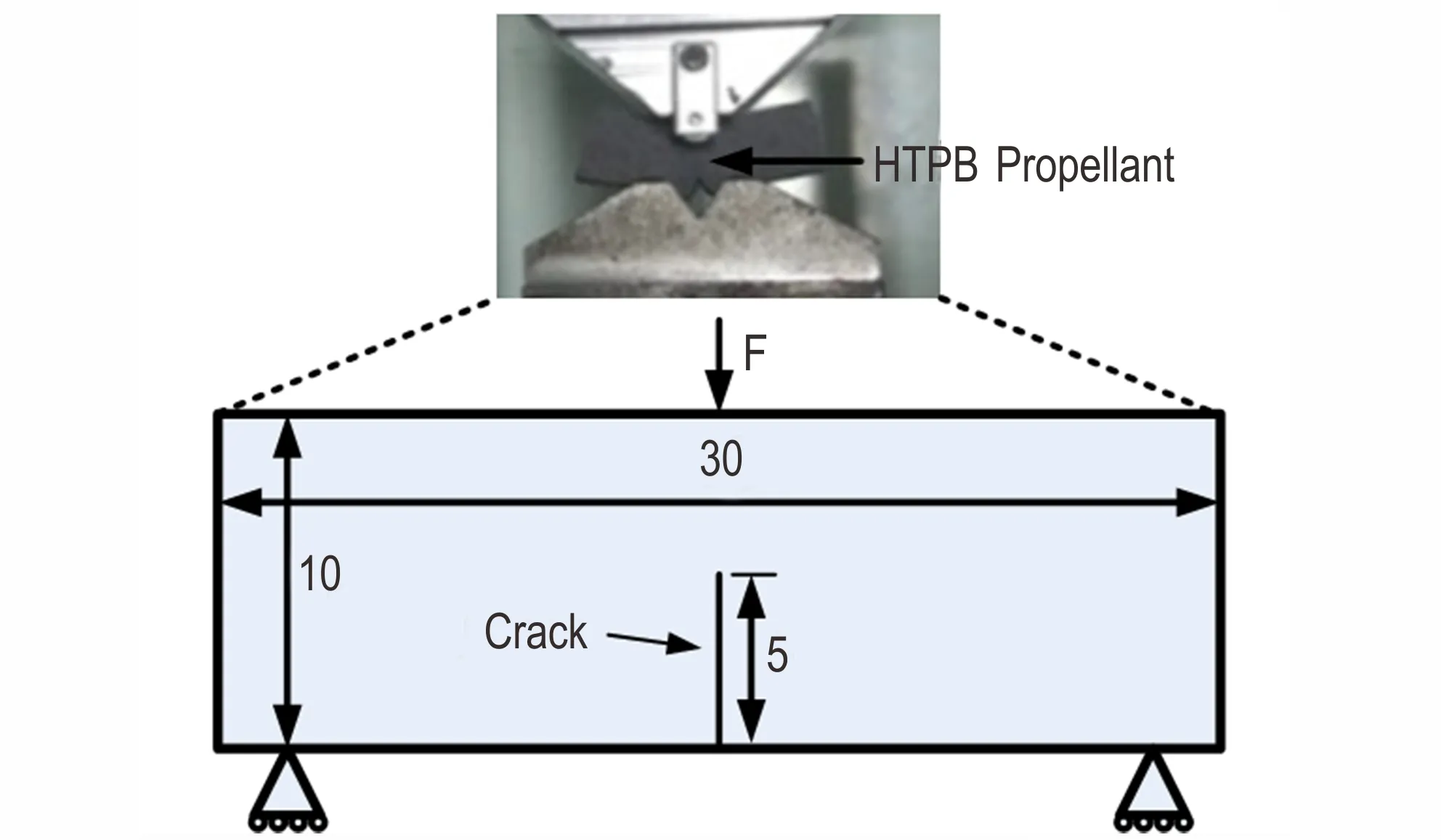
图1 试件尺寸及夹具安装(单位:mm)Fig.1 Schematic diagram of specimen size and its fixture(unit:mm)
2.2 实验过程

图2 不同压缩位移下裂纹尖端形貌Fig.2 Deformation of crack tip under different compression displacements
不同压缩位移时裂纹尖端放大50 倍SEM 图像如图2 所示,这些图像清晰地反映了不同阶段裂纹尖端细观形貌变化特点。图2a 为初始时刻裂纹尖端的细观形貌,可以看出,预制裂纹的过程中导致少数颗粒破碎,但是大多数颗粒基本保持完好。压缩位移从0 增加至2.0 mm(图2b~图2e),裂纹张开角度随压缩位移的增加而变大。裂尖出现钝化,裂尖附近的颗粒脱湿形成微裂纹,微裂纹随着压缩位移的增加不断扩展。压缩位移从2.5 mm 增加至3.0 mm(图2f~图2g),微裂纹的扩展使基体颗粒界面的粘接能力减弱,基体开始承受抵抗裂纹作用的载荷,发生较大变形。裂纹尖端载荷的作用使内部薄弱处的基体发生断裂,脱湿不断汇聚,在裂尖前方形成一个明显的孔洞,如图2g 所示。压缩位移为3.5 mm 时,裂纹尖端两侧的拉伸载荷超过基体的抗拉强度,使裂尖基体发生断裂,裂纹开始向前扩展,如图2h 所示。整个过程中,远离裂纹尖端颗粒未见明显脱湿现象,裂纹尖端颗粒的脱湿以及不同颗粒间脱湿的汇聚,与裂纹尖端的作用一起,使裂纹向前扩展。
3 数值模拟
3.1 计算模型
为了定量地描述裂纹尖端的损伤过程,对其开展数值模拟研究。对于推进剂三点弯曲过程,如果只是建立宏观模型,则无法反映裂纹尖端细观损伤过程,如果建立整个试件的细观模型,则会导致计算量太大,所以本文提出对HTPB 推进剂三点弯曲动态过程进行多尺度数值模拟。其思想是在关心的裂纹尖端采用细观模型,在远离裂纹尖端区域采用宏观模型。多尺度数值模拟采用子模型方法来完成[12],建立的多尺度模型如图3 所示。宏观模型尺寸与三点弯曲试件一致,边界条件的设置与试验相同,在宏观模型中预置一条与三点弯曲试件裂纹尺寸及位置相同的裂纹。在宏观模型裂纹尖端中心切割一个尺寸为1000 μm×1000 μm子模型,对子模型进行颗粒填充处理。根据文献[13],HTPB 推进剂细观代表性单元的最小尺寸为680 μm×680 μm,本研究建立的子模型尺寸大于该尺寸,因此建立的细观模型是合理的。由于铝粉等细颗粒几乎不会脱湿,只是起到了增强基体模量的作用,所以模型中不考虑铝粉等细颗粒,建模时将细AP、铝粉等颗粒融入基体中,混合后基体的模量可以通过Mori-Tanaka 法[14]计算得到,将混合后的基体统称为基体。根据试验结果,压缩过程中,主要的损伤形式是颗粒与基体界面处的脱粘,所以在基体与颗粒之间采用内聚力模型。
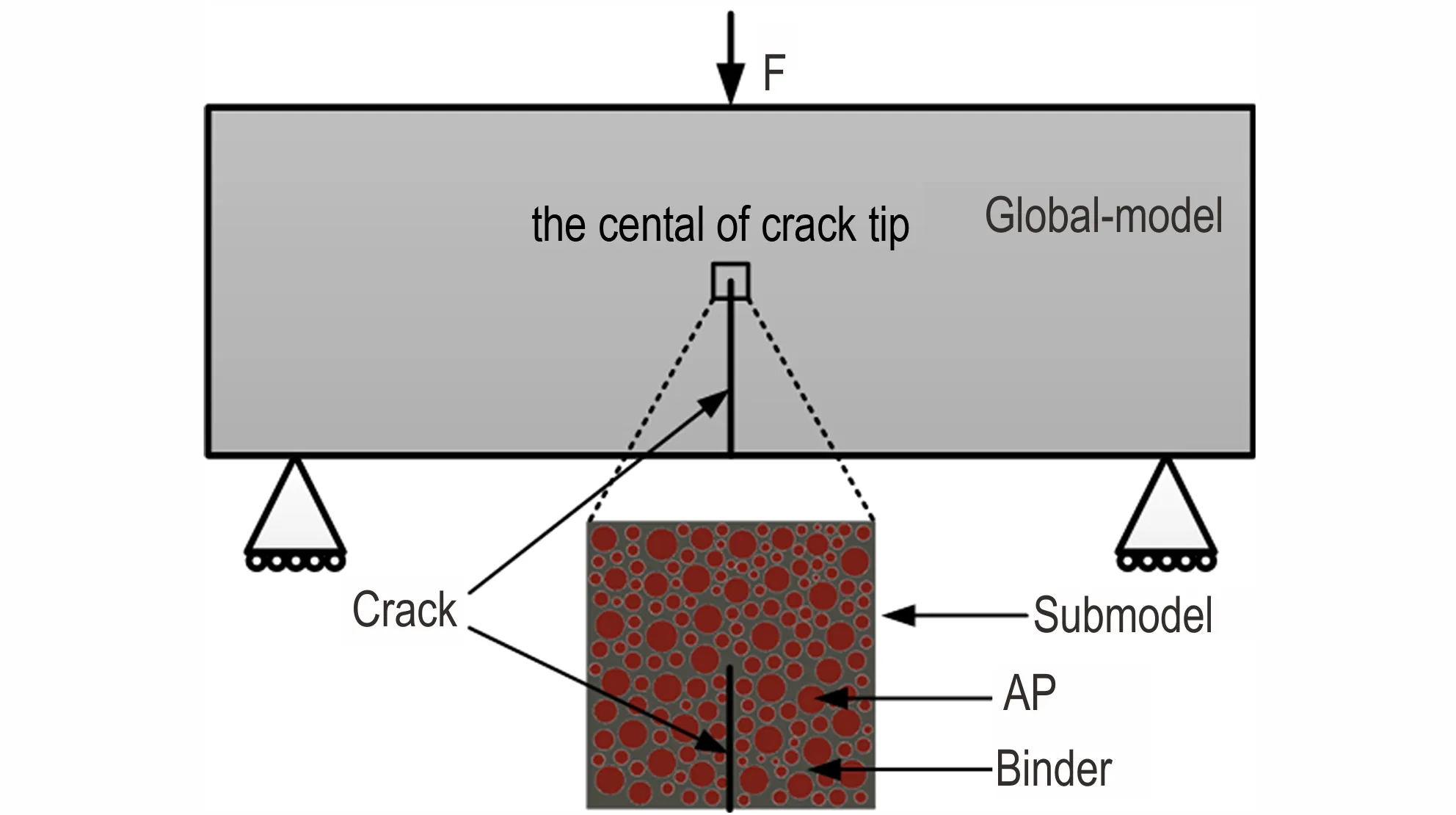
图3 多尺度计算模型Fig.3 Multi-scale computation model
子模型边界条件由宏观结果插值得到。按驱动量划分,可以分为结点驱动(Node-based submodeling)和面驱动(Surface-based submodeling),分别对应的驱动量为位移与应力,由于有限元位移计算结果精度比应力计算结果精度更高[15],所以本文采用结点驱动子模型。
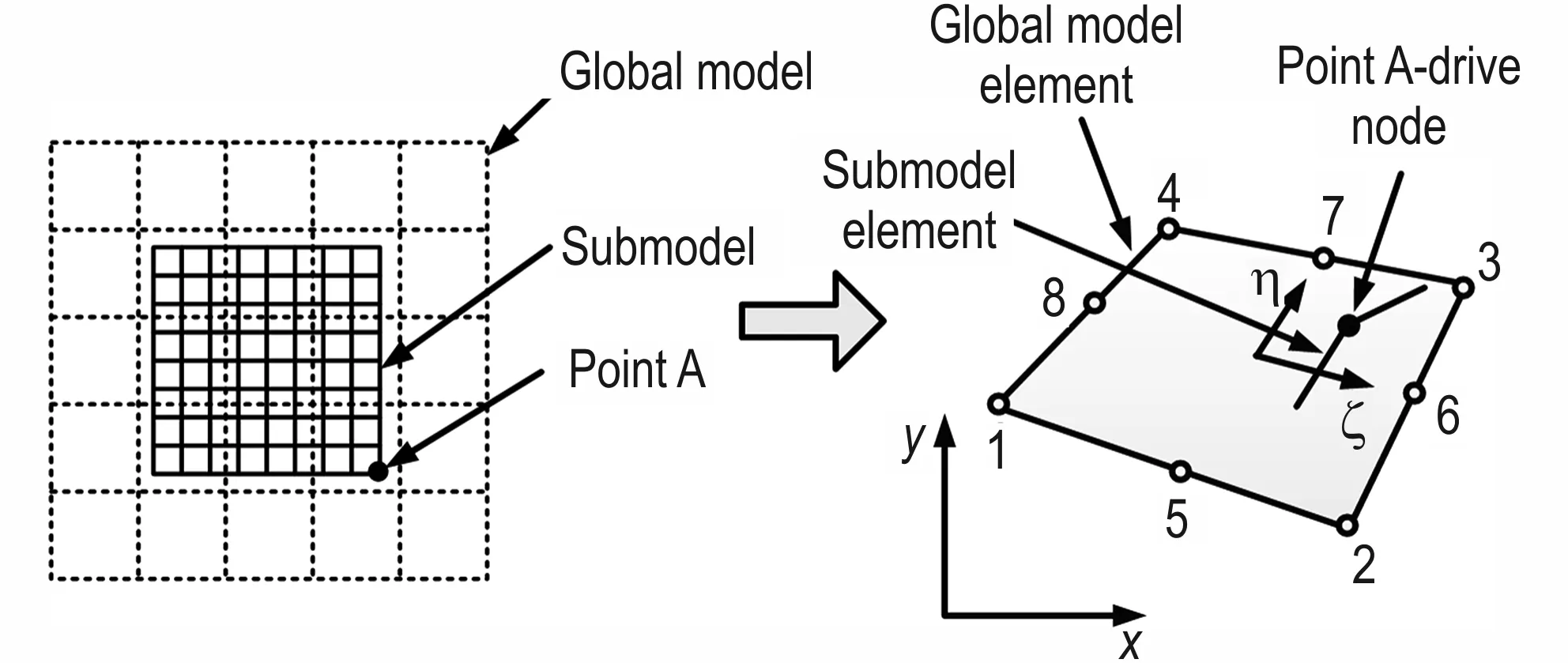
图4 子模型中驱动结点的插值方法Fig.4 Interpolation method of driven node in submodel
子模型边界在宏观模型中插值的方法如图4 所示。图4 左侧虚线区域为宏观模型,实线区域为子模型。以子模型边界上的结点A 为例,说明子模型边界插值的原理,如图4 右侧所示。(ξ,η)为基准坐标系,(x,y)物理坐标系,A 点为子模型单元的边界结点(驱动结点)。设置宏观模型的位移作为子模型的驱动量,则驱动结点A 的位移在宏观模型单元中插值得到,如式(1)所示:

式中,(ξ0,η0)为A 点在基准坐标系下的坐标,uA为物理坐标系中A 点的位移,ui(i=1,2…8)为宏观模型单元结点在物理坐标系下的位移(驱动量),N͂为基准坐标系下单元的形函数,宏观单元采用的八结点平面二次等参单元的形函数如式(2)所示。
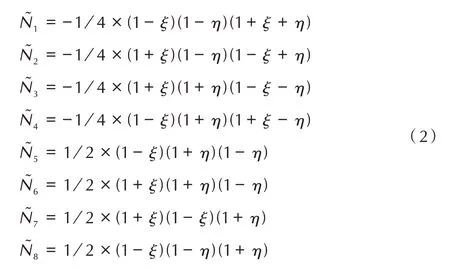
3.2 推进剂及其组分的力学本构
将HTPB 推进剂视为线弹性材料,其弹性模量E 与泊松比υ 分别为1.79 MPa 和0.495[16]。
对于HTPB 基体,采用N=3 的Ogden 超弹性本构模型,其Ogden 模型各项系数如表1 所示[17]。

表1 Ogden 超弹性模型参数[17]Table 1 Parameters of Ogden hyperelastic model[17]
推进剂中的AP 颗粒,采用线弹性本构,其弹性模量E 和泊松比υ 分别为32450 MPa 和0.1433。
3.3 颗粒脱湿的内聚力模型
内聚力模型建立了界面张开位移与界面力之间的关系,广泛用于模拟界面类问题,常用的内聚力模型有双线性内聚力模型、指数型内聚力模型、多项式型内聚力模型等[18]。本研究采用的双线性内聚力模型,其原理如图5 所示。 分为3 个阶段,损伤起始段(0 ≤δ ≤δ0)、损伤扩展段(δ0≤δ ≤δf)以及完全脱粘段(δf≤δ)。其中n、s 分别表示法向与切向,δn、δs分别表示界面的法向和切向位移分离量。
损伤起始段,界面尚未产生损伤,该阶段内界面力与界面张开位移之间的关系如式(3)所示:
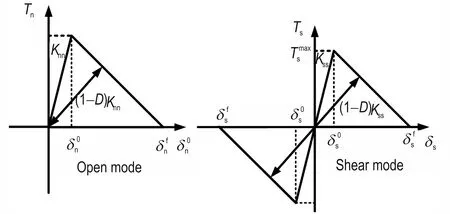
图5 双线性内聚力模型[18]Fig.5 Schematic diagram of bilinear cohesive model[18]
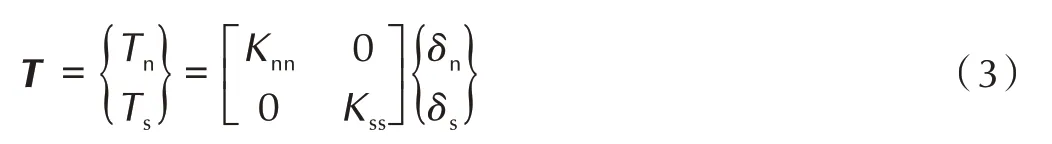
Knn、Kss分别为界面初始刚度。
损伤扩展段,界面开始损伤,界面刚度下降,此时界面位移与界面力之间的关系如(4)式所示:
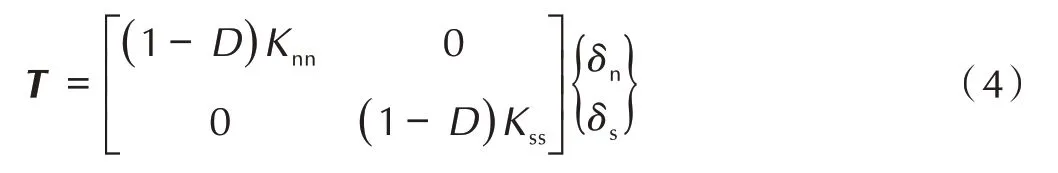
D 为界面损伤因子,如式(5)所示:



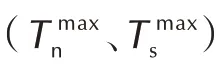

表2 内聚力模型参数[19]Table 2 Parameters of cohesive model[19]
3.4 裂纹尖端动态损伤过程分析
压缩位移较小时,颗粒脱湿较小,不易观察,压缩位移较大时,推进剂基体已经发生断裂,不易于比较。所以选取压缩位移中间值附近约为1.5 mm 时的裂纹尖端SEM 图像与子模型裂纹尖端进行对比,如图6 所示。图中上侧为宏观三点弯曲试件模拟结果,右下侧为子模型中裂纹尖端模拟结果,左下侧为试验拍摄裂纹尖端细观形貌,从图中可以明显地看到位于裂尖附近处颗粒的脱湿以及脱湿之后形成的微孔洞,试验结果与数值模拟结果比较吻合。子模型方法能够较好地反映宏观三点弯曲过程试件宏观变形与裂纹尖端细观损伤过程的特点,避免了宏观模型无法反映裂纹尖端细观损伤的问题,同时与建立整个试件细观模型的方法相比,降低了计算量,具有明显的优势。本文建立的多尺度数值模型能够有效地反映推进剂宏观三点弯曲裂纹尖端细观动态损伤过程。
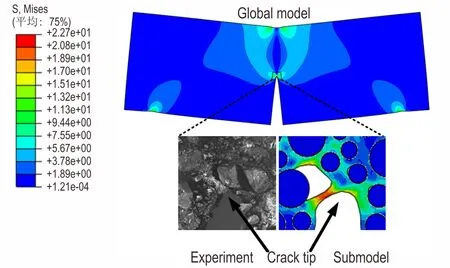
图6 试验与数值模拟结果对比Fig.6 Comparison between experimental and numerical results
图7 为不同压缩位移下裂纹尖端的Von Mises 应力云图。由图7 可知,在细观尺度下,推进剂内部的应力不是均匀分布的,颗粒内部的应力明显高于基体。压缩位移从0.5 mm 增加至1 mm(图7a、图7b),裂纹尖端的应力从0.11 MPa 增加至0.26 MPa,同时裂尖开始钝化。压缩位移为1.5 mm 时(图7c),裂尖处的颗粒发生了脱湿,出现微裂纹,脱湿之后基体受到裂纹两端的拉扯作用发生较大变形,内部应力增大。位移从2.0 mm 增加至2.5 mm(图7d、图7e),随压缩位移的增加,沿裂纹尖端向前方向的颗粒不断脱湿,脱湿后颗粒基体界面承受裂纹载荷作用的能力减弱,抵抗裂纹作用的载荷主要由脱湿后的基体承受,其内部的应力较周边区域高。压缩位移为3.0 mm(图7f),可以看出,脱湿后的基体内部应力远远高于周边区域,应力极值约为0.74 MPa。根据Von Mises 屈服准则,失效将会首先发生在这些应力较高的基体处,使颗粒之间的微裂纹汇聚,与裂纹尖端的作用一起,使裂纹扩展。整个过程中,远离裂纹尖端两侧的颗粒基本不会发生脱湿。裂纹尖端变形、损伤过程数值模拟结果与试验现象一致。
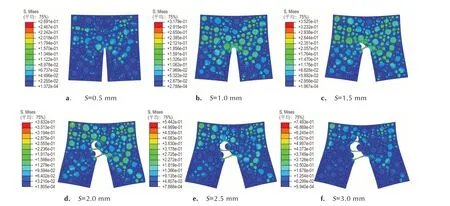
图7 不同压缩位移下Von Mises 应力分布云图Fig.7 Contours of Von Mises stress at different compression displacements
图8 为不同压缩位移下裂纹尖端的最大主应变云图。由图8 可知,与颗粒相比,基体模量较小,所以应变主要位于基体内部。压缩位移从0.5 mm 增加至1.0 mm(图8a、图8b),应变极值位于裂尖处,应变从0.5 mm 时的0.39 增加到1.0 mm 时的0.84。颗粒脱湿之后,应变最大的位置由裂纹尖端转移至脱湿之后的基体(图8c)。继续增加压缩位移,沿裂尖向前方向颗粒相继脱湿,脱湿之后的基体受到裂纹两侧拉伸载荷的作用,应变增大。压缩位移为3.0 mm 时,应变极值位于颗粒脱湿之后的基体处,约为1.72。
COD 理 论[20](Crack Opening Displacement,裂纹张开位移)认为:“当裂纹张开位移δCOD达到材料的临界值时,裂纹即发生失稳扩展”,因此裂纹张开位移对衡量裂纹是否扩展具有重要意义。对子模型中压缩起始(S=0 mm)至裂尖首次出现颗粒脱湿(S=1.2 mm)阶段裂纹张开位移进行了测量,裂纹张开位移随压缩位移变化过程如图9 所示。可以看出,裂纹张开位移随压缩位移的增大逐渐增大,当压缩位移从0 增加至1.2 mm 时,裂纹张开位移从0 增加至84.1 μm。
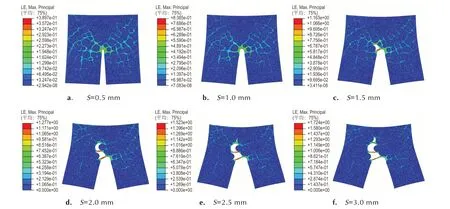
图8 不同压缩位移下应变分布云图Fig.8 Contours of strains at different compression displacements
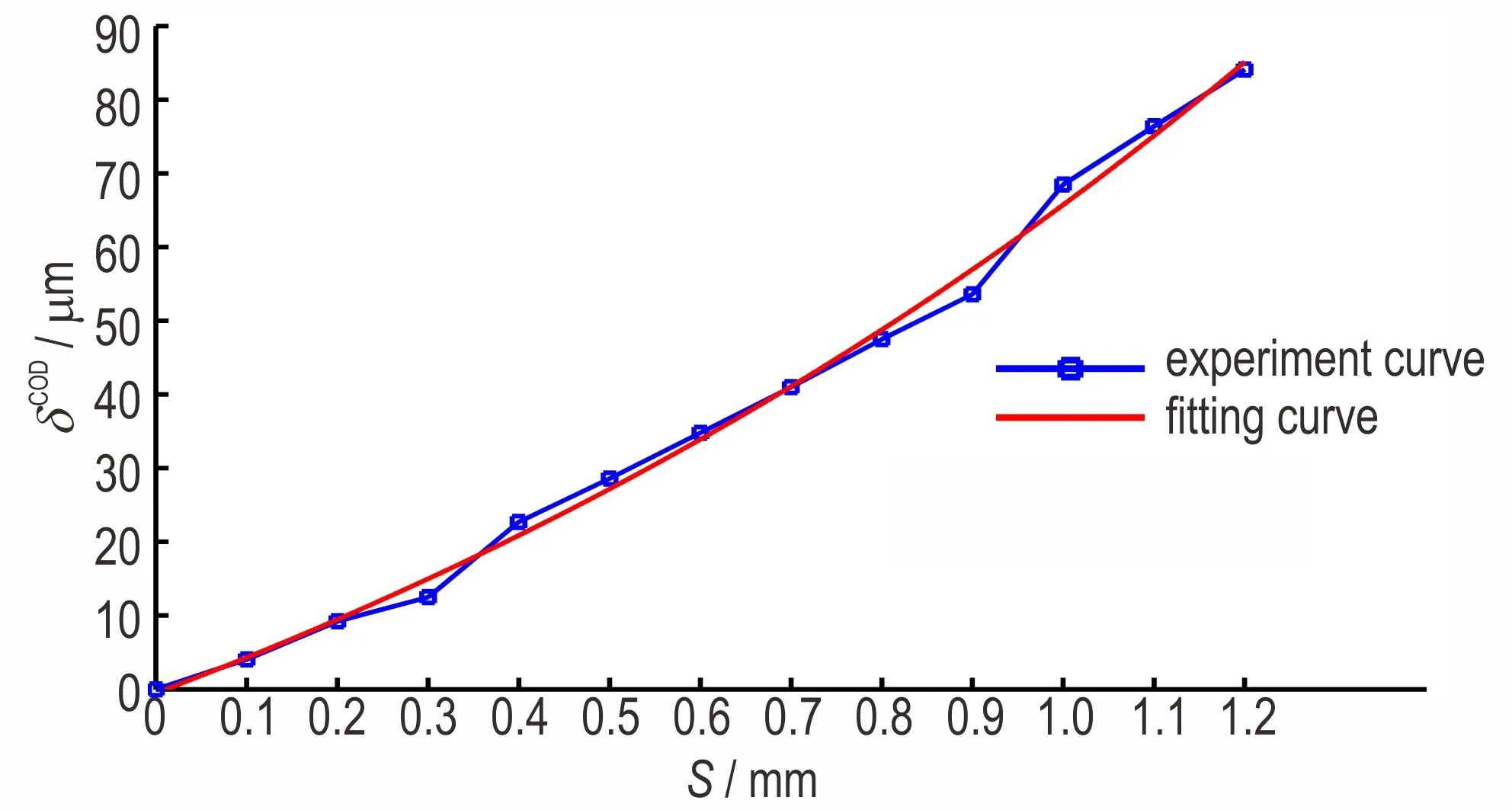
图9 裂纹张开位移与压缩位移关系Fig.9 The relationship between compression displacement and δCOD of crack tip
为排除测量过程误差的影响,将裂纹张开位移与压缩位移进行了拟合,发现裂纹张开位移与压缩位移之间比较符合指数型关系,得到如式(8)所示关系(R2=0.9961)。式(8)表明,裂纹张开位移不仅随压缩位移的增大而增大,而且增加的速率也增大。
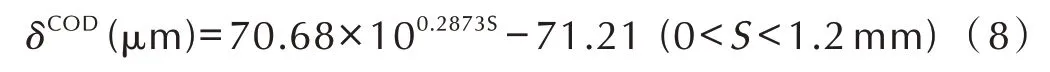
分别对试验与数值模拟压缩位移为1.0 mm 时裂纹张开位移进行测量,如图10 所示。试验过程实测值约为78.92 μm,子模型模拟值约为68.5 μm。实测值较模拟值稍大,对比试验过程裂尖与数值模拟裂尖形貌,分析其原因,主要有两点:一是试验结果中,颗粒与裂纹裂尖的距离较数值模拟中更近,裂尖两侧对基体的作用更大,基体受拉伸作用更严重,所以裂纹张开位移更大;二是由于预制裂缝的原因,造成了推进剂裂尖处初始损伤,使裂尖颗粒在压缩初期就开始脱湿,脱湿之后颗粒/基体界面承受裂尖两侧拉伸作用能力减弱,抵抗裂尖两侧拉伸作用主要由基体承受,所以基体变形更大,造成裂纹张开位移更大。而数值模型中颗粒/基体界面粘接良好,所以裂纹张开位移较小。总的来说,两者之间相差较小,再一次印证了模型建立的合理性。

图10 试验与数值模拟裂纹张开位移Fig.10 Comparison of crack opening displacements of experiment and numerical simulation
本文在分析推进剂裂纹尖端的损伤过程中,只考虑了裂纹尖端颗粒的脱湿,然而裂纹尖端的破坏是一个复杂的过程,还存在其他不同的损伤模式,比如基体的损伤等。为了更加精确地模拟裂纹尖端损伤过程,后续的研究还需考虑基体的损伤,从而更好地解释推进剂裂纹尖端的损伤机理。
4 结论
(1)推进剂三点弯曲过程中,裂纹尖端的损伤模式表现为先是裂尖颗粒与基体脱湿,在裂纹尖端附近形成损伤区,随压缩位移的增加,不同颗粒脱湿形成的微裂纹不断汇聚,在裂纹尖端两侧的拉伸作用下,与裂纹尖端合并,使裂纹向前扩展。
(2)推进剂在压缩过程中,裂纹尖端的基体受到裂纹尖端两侧的拉伸作用逐渐发生钝化。裂纹张开位移随压缩位移增大而增大,压缩位移从0 增加至1.2 mm 时,裂纹张开位移从0 增加至84.1 μm,并且其增加的速率也增大。
(3)针对推进剂裂纹尖端损伤特点,建立了推进剂三点弯曲宏细观多尺度数值模型,得到了裂纹尖端细观动态损伤过程应力应变分布与裂纹张开位移。数值模拟结果与试验结果比较吻合,有效地模拟了推进剂宏观变形与裂纹尖端细观损伤过程,为开展推进剂宏细观损伤分析提供了一种新的方法。

