基于二维浅水方程的城市地面洪水演进数值模拟研究

冀永鹏，张洪兴，王运涛，李 晋,张明亮

(1.大连海洋大学 海洋科技与环境学院，辽宁 大连 116023；2.大连理工大学 港口、海岸与近海工程国家重点实验室，辽宁 大连 116025；3.大连理工大学 水资源与防洪研究所，辽宁大连 116025；4.盘锦鸳鸯沟国家级海洋公园管理办公室，辽宁 盘锦 124010)

1 研究背景

近年来随着城市化速度的加快，城市及周边区域自然状态下的森林植被、湖泊沼泽等区域逐步被城市道路、建筑等基础设施所取代，其下垫面的不透水面积不断增加。城区下垫面性质和功能的变化致使城市的水循环途径发生了改变，某种程度上增加了城市雨洪的地表径流量[1]。再加上城市建设中排水设施存在诸多隐患和问题，导致城市雨洪和内涝灾害频繁发生，造成城区居民人员伤亡以及巨大经济损失。基于此，关于城市内涝成因、地表洪水演进预报及内涝防治等关键问题的研究受到越来越多学者的关注。作为研究城市内涝问题的重要技术手段，城市雨洪数值模拟技术是城市防洪减灾的关键技术之一，也是当前研究的热点问题。目前，国内外已经发展了很多城市雨洪模型，城市雨洪模型包括地面雨洪产流、地面雨洪汇流以及地面雨洪管流的计算，其中产、汇流计算是模拟城市雨洪过程的关键。美国环保署研发的SWMM模型[2]、美国工程师协会水文工程中心的Storm模型以及英国Wallingford水力学研究机构开发的 InfoWorks CS软件模型等[3]是根据水文学原理建立的城市雨洪模型。还有很多学者依据水动力学原理建立了城市雨洪模型，一维和二维水动力模型是应用较为广泛的模型。例如丹麦水资源及水环境(DHI)研究的MIKE FLOOD模型[4]；Cea等[5]在二维浅水水动力方程的基础上提出了解耦离散模型(DHD)，用于求解陆地径流和降雨径流的转换，并通过一些实验室案例对模型进行了验证；余江顺等[6]应用以水动力学为理论基础的水利软件(HydroInfo)对成都绕城公路区域雨洪演进进行了模拟；Xia等[7]基于浅水动力方程提出了一种新的一阶Godunov型有限体积法模型 (SRM)，使用HLLC格式计算界面通量，对城市雨洪的理想案例以及实验室案例进行了验证。由于城市地形变化大，水动力学模型的计算比水文学模型繁杂，且初始值以及边界条件的设置较为复杂，所以目前对水动力学模型的应用相对较少，但由于水动力学模型的模拟准确度更高，越来越多的学者开始关注水动力学模型的应用。也有学者建立水文学与水动力学耦合模型对城市洪水进行模拟[8-10]。另外，相比国外模型，国内模型的二次开发能力弱，模型功能也较为单一，应用范围较为狭窄，可视化水平也有待提高[11]，并且大多模型在城市雨洪模拟中并未考虑到对干湿边界水流交替进行特殊的处理。

本文基于平面二维浅水方程，在非结构网格下采用Godunov型有限体积法建立二维水动力模型，以Roe格式的近似黎曼解计算三角网格的界面通量，并且针对复杂地形进一步对干湿边界以及负水深问题进行了处理，利用第一个算例对模型的动边界处理进行了验证，利用第二个算例对模型的静水和谐性及稳定性进行了验证，并将模型应用于城市街道及附近区域的地表雨洪演进模拟，验证模型在城市复杂地形上进行洪水预测的准确性，最后使用模型对浑太胡同内的洪水演进进行了模拟预测。

2 水动力模型

2.1 平面二维浅水模型

平面二维浅水模型是对Navier-Stokes方程进行垂向平均近似，并遵循浅水Boussinesq假设所得到的控制方程。本文忽略了二维浅水方程中的风应力、科氏力和二阶扩散项，二维浅水控制方程最终可以表达为：

(1)

式中：U为守恒性变量；F和G分别为x方向和y方向对流通量变量；S为源项。

(2)

式中：h为水深，m；u和v分别为x和y方向的流速，m/s；Ri为降雨强度，mm/h；g为重力加速度，m/s2；η为水位，m；τbx和τby分别为x和y方向的摩阻项，τbx=n2u(u2+v2)1/2h-4/3，τby=n2v(u2+v2)1/2h-4/3；n为曼宁系数。

2.2 数值离散

本文采用有限体积法，以非结构三角网格为控制单元对控制方程进行离散，运用 Green 公式对控制体进行积分整理可得：

(3)

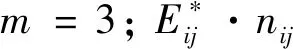
本文模型为显格式计算模式，下一时刻的离散值由上一时刻求得，其表达式为：

(4)

2.3 边界通量计算

由于对方程进行深度平均积分，物理变量在每个三角网格单元中均为常数，在整个求解域内构成一系列分片函数，非结构网格在每个控制单元边界有间断现象，形成了局部的Riemann问题。本文采用Roe格式求解Riemann问题，数值通量表达式为：

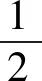
(5)

2.4 变时间步长

本文控制方程求解采用显格式计算，因此用CFL条件来控制其稳定性。在非结构三角网格下，应用CFL条件来确定时间步长[12]，其计算方法为：

(6)

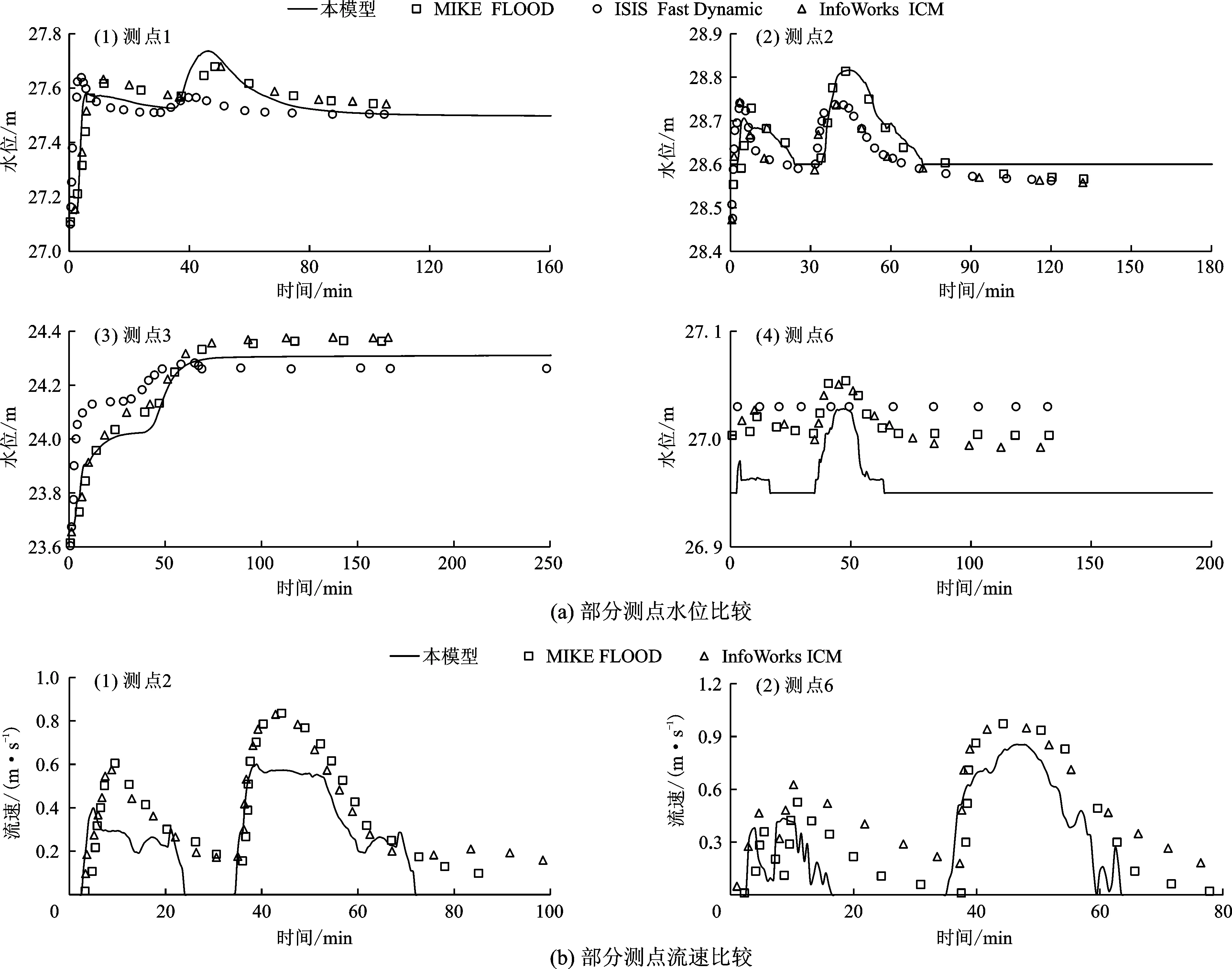
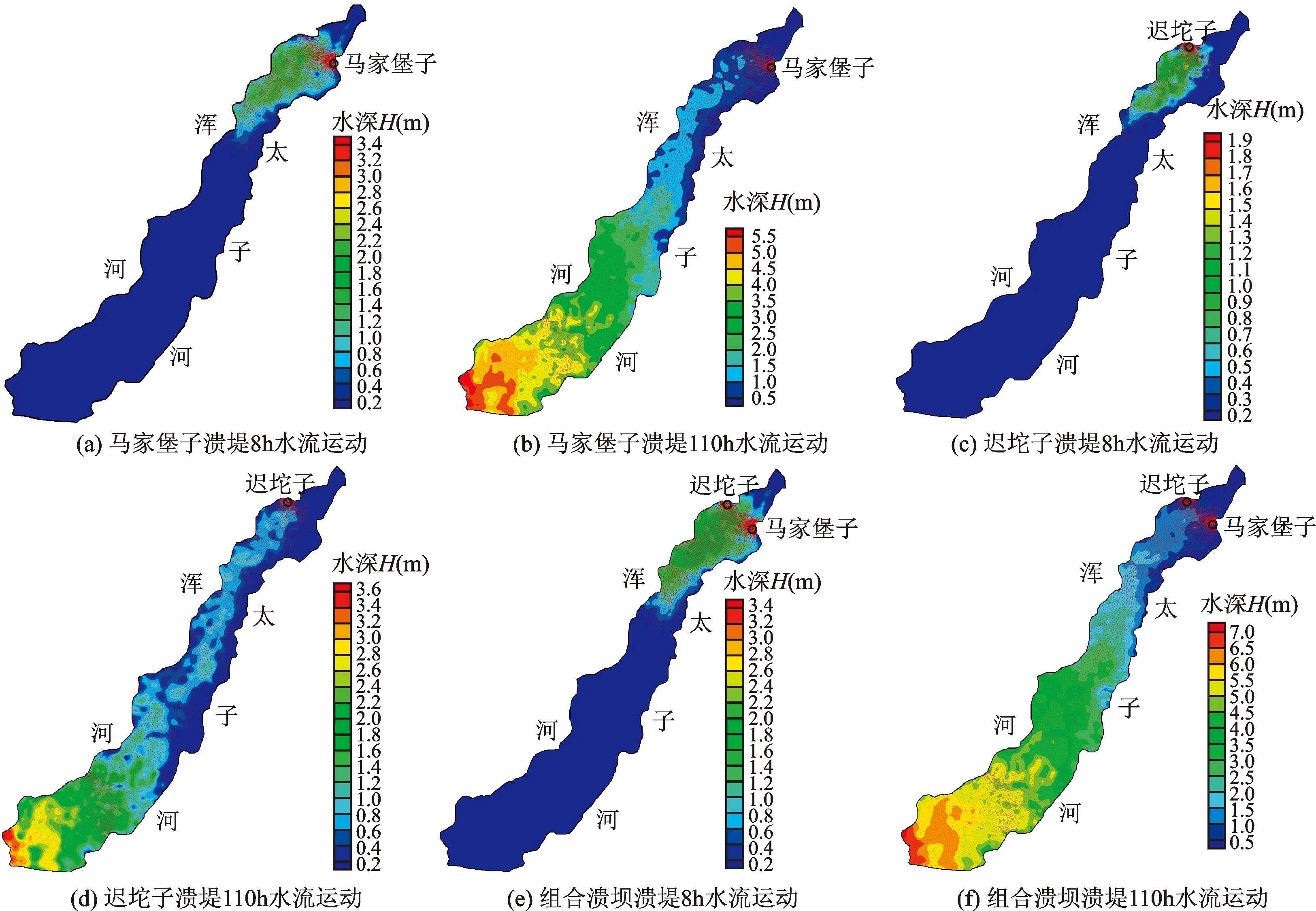
式中：Cr为库朗数，取值范围是0

3 动边界及负水深处理

3.1 动边界处理

由于城市下垫面并不平坦，降水后城市下垫面会出现局部积水现象，从而导致非结构网格单元出现干湿交替或者部分淹没的情况，形成干湿界面即动边界。

本文针对复杂地形引入了干湿界面处理技术[13]，设置了最小限制水深h0，水深大于h0即为湿边界，小于h0即为干边界。4种干湿边界分类情况如图1所示。图1 (a)中为湿边界，边界两侧水深均大于h0；图1(b)、1(c)均为半湿边界，其中图1(b)中边界有通量，图1 (c)中边界无通量；图1(d)为干边界，边界两侧水深均小于h0。

图1 4种干湿边界分类示意图

根据干湿边界的判断，可进一步确定网格单元的干湿情况：网格边界均为湿边界或有通量的半湿边界则为湿网格；网格边界均为干边界或者无通量的半湿边界则为干网格；其余均为半湿网格。在无通量半湿边界，由于ηL与ηR并不相等，形成的非物理流量会产生质量不守恒问题，所以将网格单元的ηR降到与左侧网格单元的ηL相等的位置(图1(c)虚线所示)，但这种处理仍会导致伪流速问题的出现。本文针对无通量半湿边界处的伪流速问题做了进一步处理，由于网格单元的水位梯度最终由网格节点水位决定，因此将无通量半湿边界处节点的水位降至与左侧网格单元的ηL水位相等，保证了质量守恒的同时也避免了伪流速的形成，提高了模型的静水和谐性和稳定性。

3.2 负水深处理

在基于平面二维浅水方程进行模拟的过程中，边界通量的计算由时间步长、单宽通量以及边界长度决定。若时间步长设置过小，则会极大地降低计算效率，而在小水深情况下，时间步长设置较大就会使得网格边界通量大于上游网格的水量，导致边界上游网格水深成为负值，形成负水深，最终造成质量不守恒。

针对负水深问题，本文将周围网格单元最小限制水深h0以上的水量填补入负水深网格单元中，直至负水深成为最小限制水深，从而保持质量守恒，也能保证周围网格不会因水量填补而再次出现负水深。

4 数值模拟验证

4.1 抛物型无阻力自由水面模拟

本算例模拟了在无地面阻力情况下，抛物型地形中自由水面的震荡过程。Thacker[14]给出了该情况下自由水面震荡情况的解析值。该算例是验证非平底地形条件下模型处理干湿界面交替时水流运动精度的经典案例。抛物型地形公式为：z(x，y)=h*/a2(x2+y2)，其中h*和a为大于0的常数。当σ

σ)+h*-z(x,y)]

(7)

u=-σwsin(wt)v=-σwcos(wt)

(8)

式中：σ为周期性运动的幅度；w为周期性运动的频率。在本算例中a=8 025.5 m，h*=10 m，σ=a/10，水流运动周期为3 600 s。该算例中模拟了3h，即3个周期的水流运动；采用了41 276个网格,共有20 889个节点；模拟区域为矩形，x与y方向范围均为-10 000～10 000 m，四周边界为固定边界。模拟的最小限制水深为0.01 m，曼宁系数设置为0。

模拟了y=0沿线在t=5 400 s、t=7 200 s时刻的水位，另外模拟了研究区内坐标为(-7 900，0)、(-5 500，0)两个测点的水深和流速，模拟的数值解与解析值的比较见图2～3。由图2可以看出，每个时刻y=0沿线的水位模拟值与解析值基本吻合，水位震荡幅度在8～14 m之间,且在无阻力情况下，随着时间的增加,水位的震荡幅度并未减小；由图3可以看出，水深和流速模拟结果良好，坐标为(-5 500，0)的测点处于完全淹没状态，坐标为(-7 900，0)的测点位于干湿交替处，水深和流速模拟值在干湿交接界面处没有明显波动，准确地模拟了复杂干湿界面的水流运动情况，说明模型对动边界的处理较为合理。

图2 不同时刻y=0 沿线水位模拟值与解析值对比

图3 研究区内两个测点的水深及流速模拟值与解析值对比

4.2 洪泛漫滩洼地填充模拟

本算例是模拟漫滩洼地区域洪水运动的理想算例，涉及到复杂地形上低动量流的运动情况，主要验证模型的动边界处理能力、静水和谐能力及稳定性[15]。图4所示为模拟区域等高线、测点以及入流位置分布，模拟区域为2000 m×2000 m的矩形区域，由4×4的洼地矩阵组成，各个洼地形状一致，地形变化平滑，沿西北向东南对角线地形高程下降2 m。测点均分布于洼地中心，洼地序号(亦为测点编号)如图4所示。入流分布于西北角向南延伸100 m，入流流量为20 m3/s，从第10 min开始持续到86 min，其他边界均为固壁边界，没有流量流出。该算例模拟区域采用了26 508个网格，初始状态为干河床，时间步长为变化时间步长，最小限制水深为0.003 m，曼宁系数设定为0.015，共模拟了48 h。

图5为不同模型计算的部分测点水位随时间变化的比较。所参照对比的模型包括MIKE FLOOD[4]模型、InfoWorks ICM[10]模型以及ISIS Fast Dynamic[15]模型。MIKE FLOOD模型是基于一维和二维水动力模型进行动态耦合的建模系统。InfoWorks ICM模型是基于有限体积法的二维水动力浅水方程建立的模型，模型具有模拟自然界水流运动以及工程排水系统的能力，并且可以捕捉快速流动的水流变化。ISIS Fast Dynamic模型是利用曼宁均匀流动定律，基于体积扩散法建立的模型，模型可以预测洪水的最后淹没程度以及类似于二维浅水在低动量流情况下的水流动态，但不适于预测洪水的淹没速度。从图5中可以看出，本模型模拟结果与其他模型结果均大致相符，虽然结果有时存在有一定的数值差异，但水位的变化趋势是基本一致的。当入流流量开始进入时，在入流点附近测点(测点4、7)的水位可以观测到瞬时水位峰值。入流消失后，附近测点的水位会逐渐下降，直至洼地边缘最高处洪水无法流出洼地则水位达到平衡。离入流点越远的测点瞬时水位峰值会逐渐变小甚至消失。测点5、10的水位变化波动较大，比其他模型的水位到达时间要早大约5～9 h，两个测点的水位相比其他模型也较高。这主要是由于洼地之间区域最小限制水位以上的水深较浅，而限制水位以上的水深有着微小的差异就会导致水位的大小以及水位随时间的变化表现出显著的不同。

图4 漫滩洼地模拟区域等高线、测点及入流位置示意图

图5 漫滩洼地区域洪水演进算例不同模型计算的部分测点水位随时间变化的比较

图6为第6、12 h的水深淹没范围与流场分布。分析图6可知，水流沿着地势方向向下流动，在计算区域东西方向地形平坦,水流速度缓慢，南北方向地形有较大起伏，水流速度较快，水流平稳后的洼地四周几乎没有流速的分布也说明了模型对伪流速处理的合理性。

综上所述，该模型对本算例的模拟较为良好，模型的动边界处理较为合理，静水和谐性较好，可以应用于模拟和预报城市雨洪形成的地表径流演进过程。

图6 漫滩洼地区域第6、12 h的水深淹没范围及流场分布

4.3 城市降水及点源径流洪水演进模拟

本算例的模拟区域位于英国格拉斯哥的科肯齐街及周围街道，忽略了街道以外的下垫面以及建筑[15]。模拟区范围面积约为0.4 km×0.96 km，地形及道路分布、点源径流的入流点、测点分布位置见图7，地形数据分辨率为0.5 m。城市洪水的来源有两种：一是降雨径流，二是地面的点源径流。模拟降水时间为1～4 min，降雨强度为400 mm/h，模拟入流流量从第23 min开始逐渐增加，在37～39 min达到5 m3/s，随后流量逐渐减小，在53 min时停止入流。模拟采用了21 261个网格，区域四周边界均为固壁边界，模拟初始状态为干河床，时间步长为变化时间步长，共模拟了5 h的洪水演进过程。道路路面的曼宁系数为0.02，其余下垫面曼宁系数为0.05。图8(a)显示了1、2、3、6测点本模型模拟的水位与其他模型模拟水位的比较，对比模型同样包括有4.2中所述的各类模型。从图8(a)中可以看出本模型模拟水位与其他模型水位变化趋势基本一致，都呈现“双峰”的形态，这是由于在t=1 min到t=4 min时发生了强降雨，而点源入流量峰值在t=37 min时出现。由于测点3位于下游聚洼地，其由降水形成的水位峰值持续了近30 min，而点源入流形成的峰值也出现了滞后且水位逐渐保持在一定高度。本模型模拟的流速与其他模型模拟流速的比较如图8(b),由于ISIS Fast Dynamic模型无法预测速度，因此对比模型仅包括MIKE FLOOD以及InfoWorks ICM模型。图8(b)显示，各模型预测的速度变化趋势大致相同，同样都呈现“双峰”状态，但数值之间存在较大差异，这可能是由于各模型采用的计算方法和格式不同，或者地形影响、水深极浅区域处理方式的不同所引起的。总体上来说，本模型能够处理干湿交替的复杂水流运动，能够较为准确地模拟城市雨洪的演进过程。

图7 研究区地形及道路、入流点、测点分布

4.4 浑、太河溃堤洪水在浑太胡同的演进

浑太胡同位于鞍山市温香镇，左邻浑河右邻太子河，两条河流共同汇入形成大辽河，由大辽河河口流入辽东湾海域。每年夏季强降雨会对浑河、太子河汛期的水位产生极大的影响，据历史资料统计，浑河及太子河曾频繁发生溃堤洪涝灾害，在从1798年到1997年近200年时间里，一共发生了114 次不同程度的水灾，发生频率为每1.75 a一次。其中1898年到1997 年间，发生了20次大面积洪水和内涝灾害，辽、浑、太3河均包括在受灾区域内。另外，连续多年发生水灾的次数也很频繁，近200年里，连续 2 年以上发生水灾有22次，而且有些年发生的是较大洪水，对浑太胡同内的城区造成了极大的损害[16]。

本文以浑太胡同为研究区域，利用本文模型对浑、太河内100年一遇的特大降雨造成的溃堤洪水进行了数值模拟。模拟以Roe格式求解二维浅水控制方程，基于改进的动边界处理以及负水深处理技术，提高了模型在复杂地形下模拟的稳定性和精度。马家堡子在浑太胡同历年发生的洪涝灾害中多次形成溃口，如1949和1950 年发生的溃堤洪水灾害。因此，本文首先选择马家堡子作为溃口位置，并且选择了同在上游的迟坨子作为另一个溃口，首先模拟单个溃口情况下特大洪水在分布有城区和村庄的浑太胡同中地表水流的运动状况；然后将两个溃口进行组合，模拟两个溃口同时溃堤形成的特大洪水在浑太胡同中地表水流的运动状况。模拟区域非结构三角网格共12 659个，溃口位置处设置为入流边界，溃口入流边界网格长度较小，设置为80～100 m，为了减少计算量，其他区域的空间网格划分尺度较大。特大降雨形成的径流由入流边界进入，其余边界均为闭边界。模拟中曼宁系数设置为0.05，采用变化的时间步长，模拟方案总时长为118 h。图9为研究区内不同工况下溃堤洪水的淹没范围以及流场分布。

图8 城市降水及点源径流洪水演进算例不同模型计算的部分测点水位及流速比较

图9 浑河和太子河溃堤洪水模拟不同工况下溃堤洪水在浑太胡同的水流演进

从图9中可以看出，洪水由东北方向向西南方向演进，与浑太胡同地势东北高西南低相符合。随着溃口入流流量的进入，淹没面积不断扩大；在入流流量逐渐减弱后，上游水深明显下降，洪水不断向下游聚集，最终在下游处出现最大水深，马家堡子、迟坨子以及组合溃口的最大淹没水深分别为6.25、3.94以及7.44 m。同时也能看出，在入流径流减弱后的洪水运动末期水流流速有了明显下降，水流逐渐稳定。

图10给出了几种溃口工况下不同水深(H>0.5 m、H>1.5 m、H>2.5 m)淹没面积的比较。由图10可以看出，入流总量与各深度淹没面积成正比，组合溃口情况下各深度淹没面积均为最大。本文计算采用CPU单核串行模式，处理器型号为Intel Core CPU i7-6700 CPU@3.4GHz，模拟方案时段长度为118 h，计算耗时统计结果如下：马家堡子、迟坨子以及组合溃口分别在19、12以及21 min内完成了模拟。结果表明，本文模型效率较高，能够在较短的时间内完成大尺度洪泛区及城区的洪水预报。在模拟溃堤时，本文模型可同时模拟任意溃口、多个溃点洪水的实时演进预报。总体而言，本文模型能够较为准确地模拟城区复杂地面上洪水的演进过程，并且可以实时地为城市洪水的演进进行预测。

图10 浑河和太子河溃堤洪水不同工况下淹没面积比较

5 结 论

基于有限体积法以Roe格式求解Riemann解并对方程进行离散，改进对动边界以及负水深的处理技术，建立了非结构网格下的平面二维浅水模型。本文验证了模型的干湿边界处理能力以及静水和谐性，并将模型应用于浑太胡同溃堤洪水模拟，最终得出以下结论：

(1)模拟抛物型地形下无阻力自由水面的运动，模拟的水位、水深以及流速值与解析值吻合，特别是干湿边界处测点的模拟值基本没有明显的数据波动，因此模型具有较好的干湿边界处理能力；模拟了洪泛区多个洼地的填充过程，洼地附近的水流基本平稳后，流速明显降低，流场分布范围减小，因此模型具有良好的静水和谐性，模型能够稳定地模拟复杂地形区域的洪水运动；

(2)模拟英国格拉斯哥城市雨洪的演进过程，结果很好地反映了在降水和点源径流两种城市洪水来源下的水位与流速变化，模拟结果具有较高的精度和准确性，模型可以针对复杂地形区域进行降雨和洪水演进的模拟；

(3)在不同溃口工况下，针对鞍山市浑太胡同100年一遇的特大洪水的模拟结果表明：洪水演进方向与地势走向相符，洪水演进过程中流场分布合理，洪水流量与淹没面积呈正相关。模型在21 min以内完成了不同工况下118 h的大面积洪水演进，具有较高的模拟效率。本文模型能够在较短时间内对长时间、大范围区域的洪水进行实时地预报，为预判洪水淹没情况以及及时做出洪水治理决策提供科学的依据，对降低洪水灾害损失和人员伤亡具有重要的意义。

在实际情况中，城市的降雨洪水在城市下垫面有一定的下渗现象，所以为使模拟更加精确，在未来研究中应将降水的下渗作用加入模型中。此外，在实际的城市雨洪中，暴雨洪水造成的污染物扩散是影响城市环境的重要因素，因此城市雨洪水动力学模型与水质模型的耦合也是本模型研究发展的一个重要方向。