基于灰色系统理论的水库移民安置进度偏差预测分析

李贵博，姚凯文，张 丹 ，李宁宁

(1.广东省水利电力勘测设计研究院，广州 510000；2.华北电力大学可再生能源学院，北京 102206)

0 引 言

水库移民安置工作在整个水利工程中无论从投资还是工作量上都占有很大的比重，水库移民安置工作的顺利进行，对维护当地社会稳定，保证水利枢纽工程顺利完工有着积极的意义。为保证工程的按时完工，移民安置部门会提前制定进度计划，但由于水库移民安置工作的复杂性，在实际实施过程中，意外情况时有发生，从而导致安置工程的实际进度偏离预定的计划，严重影响了整个水利工程的按时完工，对经济、社会的发展均有着较大的影响。因此，移民安置部门需要及时掌握工程进度信息，找出进度偏差产生原因，从而采取有效措施进行进度控制，保证移民安置任务按时完工[1]。

同其他的施工类自然工程不同，水库移民安置工作涉及数以万计的移民征地搬迁等问题，在实施过程中变数更大，工作开展更加困难，具有明显的动态特征和不确定性，同时有具有信息不完备、数据少的特征。

灰色系统理论与1982年被邓聚龙教授提出，该理论主要适用于将“部分信息已知，部分信息未知” 的“小样本、贫信息”的不确定性系统作为研究对象，通过提取部分已知信息中有价值的内容，实现对系统运行行为、演化规律的正确描述和有效监控。目前，灰色系统中的GM(1,1)预测模型被广泛运用到各类工程的进度偏差分析中，并取得了不错的效果，移民安置工程符合该系统的特点，因此本文尝试采用GM(1,1)建模，探究其在移民安置工程进度偏差分析上的应用[2]。

1 灰色预测模型

灰色系统预测是通过建立灰色模型对原始数据进行累加，发现、掌握原始数据的规律，得出规律性较强的曲线，进而对整个系统做出科学合理的定量预测[3]。目前运用最普遍的灰色预测模型就是GM(1,1)预测模型，其建模过程如下。

1.1 GM(1,1)模型的建立[4]

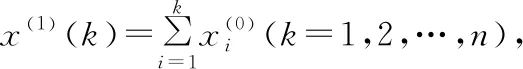
GM(1,1)预测模型的微分方程为：

(1)

式中：a、b均为常数，a称为发展系数，b称为内生控制灰数。

通过最小二乘法拟合可以得到 与 的值。具体计算公式为：

[a,b]T=(BTB)-1BTYN

(2)

其中：

(3)

YN=[x(0)(2),x(0)(3),…,x(0)(n)]T

(4)

最终求出发展系数的大小不同，其模型可进行预测的效果也不同，具体关系如表1。

表1 发展系数取值与预测效果关系表[5]Tab.1 The relation table of the value of development coefficient and the effect of prediction

预测模型微分方程的解为：

(5)

(k=1,2,…,n)

上式为累加数列的预测值公式，若想预测原始数列，可通过对上式进行累减计算得到公式：x(0)∧(k+1)=x(1)(k+1)-x(1)(k)。

1.2 模型精度检验[6]

得到预测值后，要经过检验后才能判定该模型是否合理。目前最为常见的精度检验方法有残差检验和后验差检验，下面将两种检验方法的步骤作简要介绍。

(1)残差检验。残差检验的具体步骤为：

①计算原始数列与对应模型计算值的残差：

δ(0)(k)=x(0)(k)-x(0)∧(k)

(6)

②计算原始数列与对应模型计算值的相对误差：

(7)

一般认为，当M(0)(k)<0.2时，模型的残差检验为合格。

(2)后验差检验。后验差检验的具体步骤为：

(8)

(9)

②计算均方差比c与小误差概率p，计算公式如下：

(10)

(11)

模型精度由c与p的值共同决定，具体关系如表2所示。

表2 后验差检验精度等级参照表Tab.2 Precision grade reference table of inspected by posterior difference check

2 实例应用

本文采用国内某水库移民工程作为计算实例，以移民搬迁人数来反映移民安置工作的进展情况，对其从2014年12月到2017年6月期间的六次移民搬迁人数统计数据进行偏差预测分析，在残差检验合格后，利用已知的2017年12月的数据对模型进行二次检验，确保模型在移民安置偏差预测中的可行性。

2.1 模型建立

该工程在移民安置工作初期，首先进行了移民安置试点，试点范围内207户800人的移民安置规划设计已由项目法人单独委托完成，该试点的800人不用于本次建模计算，该工程移民的全面搬迁工作于2014年开始进行。据统计，从2014年6月到2017年6月，各时间截点的累计移民搬迁人数如表3所示。

表3 工程各时间截点累计移民搬迁人数统计表Tab.3 Cumulative number of migrants at different time points in engineering

该数据为累计人数，以2014年6月的搬迁人数作为基准点，通过计算可得到原始序列，即：X(0)=(94,106,379,249,464,326)。

通过将原始数据累加计算得到累加序列：X(1)=(94,200,579,828,1292,1618)。

将求出的两个常数带入式(5)即可得到该工程移民搬迁人数的偏差预测模型，需要注意的是：由于计算以2014年6月的搬迁人数作为基准点，故在式(5)中应加入2014年6月的搬迁人数。通过计算可得：

1 430.613 7 e0.146 0 k-541.613 7

(12)

2.2 模型检验

选取不同的k值，带入偏差预测模型计算得出各时间截点移民搬迁人数的预测值，并进行残差检验及后验差检验，由表4中的结果可知，残差检验结果中，模型的相对误差均小于0.12，满足精度的要求，检验结果为合格；后验差检验结果中，均方差比为0.472，小概率误差为0.833，即0.3

现已知2017年12月累计移民搬迁人数为2 839人，现令k=6，计算2017年12月的移民搬迁人数预测值为2 894 人，相对误差仅为0.019 4，结果表明该模型在水库移民安置进度偏差预测上精度较高。另外，由于-a=0.146≤0.3，因此该模型可用于中长期预测，这也迎合了水库移民安置工作时间跨度较长的特点。

表4 工程移民搬迁人数预测模型残差检验计算表Tab.4 Residual test of migration number prediction model of the engineering

2.3 工期偏差预测分析

将除去试点搬迁800 人后的规划搬迁总人数8 812 人带入模型，求得K值为12.86，即全部移民搬迁工作完成时间预测结果为2021年5月。根据移民安置规划，该工程移民全部安置完毕的规划时间为2020年，即预测结果表明该工程的进度已经严重滞后。因此，移民安置部门要采取有效措施，加快移民安置进度，根据笔者多次实地走访调查该工程的经验，针对工程的实际情况，现提出几点加快移民安置进度的建议如下：

(1)进一步提高认识，明确责任，加强对水库移民工作的组织领导。各有关镇(办)要切实落实镇政府是水库移民安置工作的“责任主体、工作主体、实施主体”三个主体责任，要进一步统一思想、提高认识，加强领导、落实责任，严格按照县委、县政府的部署要求，实行各级“一把手”负总责、分管领导具体负责的工作机制，相关镇(办)要进一步调整优化移民工作机构，至少确定2名责任心强、对农村工作熟悉的业务骨干具体开展此项工作。

(2)做好水库移民政策宣传。针对库区移民对移民搬迁政策掌握不准，理解不清等问题，各镇(办)要加大移民政策宣传培训力度，通过入户宣讲、发放宣传册、开村民大会等多种形式认真宣传水库移民搬迁安置有关政策，使移民政策在库区进村入户，做到家喻户晓，消除移民群众政策上的疑虑，解除搬迁顾虑。

(3)及时、高效地签订移民搬迁安置协议。各镇(办)要依据相关文件，对移民户数、人口和实物指标进行搬迁前的最后核定，依据核定的移民人口和实施补偿补助项目内容，及时与接安地镇(办)对接，组织与移民户签订搬迁安置协议，协议中应明确安置地点、搬迁时间、建房方式等有关内容，必要时，各镇(办)组织对搬迁安置协议进行公证，对符 合安置政策的移民做好资金兑付工作。

(4)切实做好已搬迁安置移民的后续工作。为确保移民“搬得出，稳得住，能逐步致富”，各镇(办)要对已搬迁安置的移民及时接转户口等关系，拆除库区房屋附着物，做好已安置移民的生产生活保障。

3 结 语

根据模型检验的结果，证明了GM(1,1)模型在水库移民安置进度偏差预测上的可行性，灰色系统理论为移民安置机构在工程进度控制上提供了一定依据，使其可随时掌握工程进展的快慢，是否能够按计划完工，从而及时采取有效措施进行进度调整。通过模型计算，得到实例工程移民搬迁安置工作的完工时间将滞后一年以上，移民安置部门应从加强组织领导、做好政策宣传、及时签订协议、完善后续工作等方面来加快移民安置进度。

□