基于多损失约束与注意力块的图像修复方法

曹 真， 杨 云, 齐 勇, 李程辉

(陕西科技大学 电子信息与人工智能学院， 陕西 西安 710021)

0 引言

如今，图像已经成为我们获取视觉信息的主要途径.但由于传输不当，保存不当等许多原因，图像不可避免受到损坏，导致其关键信息无法得到传达.因此，图像修复技术应运而生，同时图像修复技术思想也可扩展到消除场景元素[1]、图像去噪等领域.

破损的人脸图像无法有效表达个人信息，保证其完整成为目前的研究热点[2,3].图像修复的主要任务是估计合适的像素信息以填充缺损图像[4].由于深度学习方法在面对大面积缺损的图像时，其处理结果往往较传统方法更逼真，更具有语义性，因此，将其应用于图像修复任务成为目前的一大趋势.

目前，基于深度学习的图像修复方法多以Goodfellow等[5]提出的生成对抗网络(GANs)作为方法基础.Pathak等[6]首先利用GANs和深度卷积提出上下文编码器网络,对于图像的大面积缺失区域恢复效果显著，恢复结果具备合理的语义信息.Raymond等[7]提出使用深度卷积生成对抗网络(DCGAN)处理图像缺失区域，首先使用训练有素的DCGAN[8]模型生成与缺失图像相似的图像，然后利用损失约束寻找最优修复块完成图像修复.Iizuka等[9]提出双判别器(GLCIC)模型通过增设局部判别器追踪局部待修复区域，有效提升了修复准确性.Li等[10]提出一种基于生成对抗网络的图像修复模型，提出全局和局部两个判别器以及语义解析模型处理图像信息.Peng等[11]提出一种基于条件生成对抗网络修复方法用于提升最终修复结果的类别准确性，Wang等[12]向生成对抗网络引入注意力机制处理图像修复问题.Lahiri等[13]对基于GANs的修复模型中增加语义条件指导模型修复图像，使得修复结果具备合理的语义性.Demir等[14]提出使用深度卷积自编码网络修复图像.Yang等[15]将图像纹理合成思想增添到编码-解码器网络模型中用于修复图像.

上述方法虽取得了优于DCGAN模型的修复效果，但其存在以下不足.首先并未添加稳定模型训练的策略且模型拟合数据能力不足，容易出现模型崩溃，梯度变化异常问题；同时，向模型提供的损失约束不足以寻找最优编码，使得生成器的输出结果往往缺少内容，风格特征或出现关键错误信息，最终导致模型修复结果欠佳.基于此，通过设计残差块和注意力块构建一种多损失约束的Multi-Loss GAN(MLGAN)模型，在相同实验环境下，对比不同模型的实验结果，本文方法修复结果更优.

1 相关理论

利用生成对抗网络(GANs)模型完成图像修复任务主要分为图像生成和图像修复两个阶段.

1.1 图像生成

通过预训练一个生成能力突出的生成对抗网络来满足图像生成的需求.该阶段需要模型满足拟合真实样本的能力.

生成对抗网络(GANs)是一种引入对抗学习思想的生成模型，由生成网络(Generator)和判别网络(Discriminator)两部分构成.近年来，由于其可以拟合更加真实的样本，在图像修复领域备受青睐.GANs的目标函数如式(1)所示.

Ez～pnoise(z)[ln(1-D(G(z)))]

(1)

式(1)中：E表示期望,pnoise(z)表示随机噪声分布集合，pdata(x)表示真实样本集合.利用该损失函数约束模型，计算损失利用反向传播更新模型参数，直至模型收敛.GANs模型结构如图1所示.

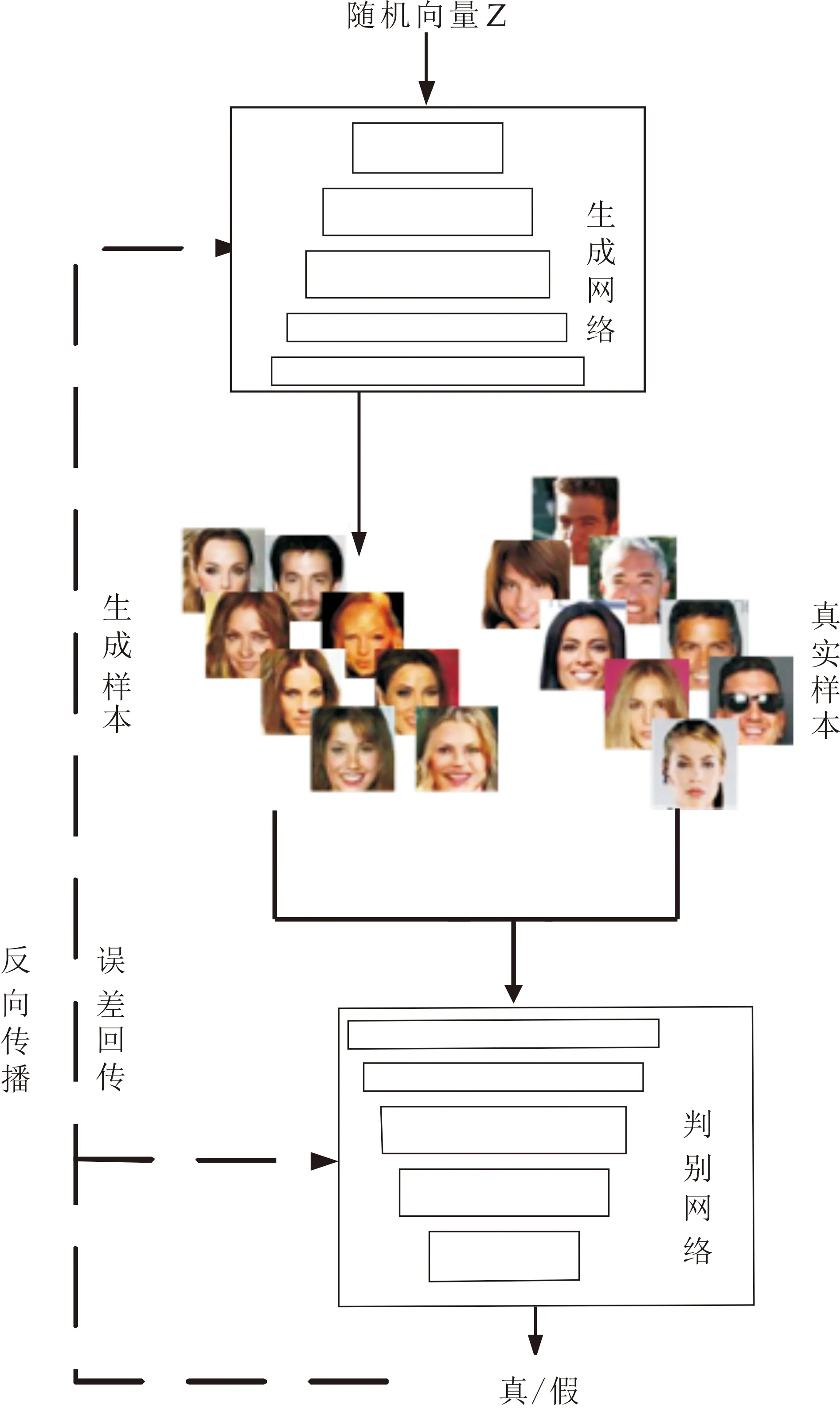
图1 GANs模型结构示意图

1.2 图像修复

通过预训练的生成对抗网络模型生成与缺损图像相似的图像，并利用感知、结构损失函数协助模型寻找最接近于缺损图像的相似图像，并截取修复块与缺损图像融合完成图像修补[7].此阶段预训练的生成对抗网络模型参数不再更新.图像修复过程如图2所示.

图2 图像修复过程示意图

其中对于一张真实样本，使用二进制掩模对其损坏构成缺损样本.利用预训练好的生成器生成一系列相似图像G(z)，将相似图像对应的随机向量z输入至预训练好的判别器中得到感知损失.感知损失如式(2)所示.

Lp(z)=log(1-D(G(z)))

(2)

式(2)中：G(z)为生成器的输出结果.

为了得到残缺图的缺失部分信息同时生成最优修复块修补残缺图，使用二进制掩模W对候选图像进行处理，W由式(3)所示.

(3)

式(3)中：Wij表示图像第i行第j列像素xij对应的掩码值，σ表示图像中的非信息缺失区域.

对于候选图像G(z)，根据残缺图的缺损位置，对G(z)添加二进制掩模，使得其与残缺图保持一致.通过比较两者剩余已知像素间的差异，最小化候选图像的结构损失，寻找最接近于残缺图的候选图像.结构损失如式(4)所示.

Lc(z|y,W)=‖W⊙G(z)-W⊙y‖1

(4)

式(4)中：y代表带有二进制掩模的缺失图像，W代表与图像尺寸相同的二进制掩模.其中⊙为Hadamard积.

2 本文方法

2.1 Wasserstein GAN(WGAN)

早期GANs模型设计存在训练不稳定，模式坍塌等缺陷.目前，针对于此缺陷主要从模型设计角度和损失函数角度改进.改进策略的主要依据是使得模型设计满足Lipchitz条件.Lipchitz条件定义为函数变化的剧烈程度，由式(5)体现.

(5)

式(5)中：x1，x2为函数f(x)定义域内的任意两点.式(5)定义了函数f(x)在其定义域内任意两点的斜率不大于一个常数D.神经网络可以看做是多层嵌套函数，因此可以根据Lipchitz条件建模.Arjovsky等[16]提出的WGAN方法，通过引入Wasserstein距离改进原有GANs的目标函数，使得模型设计满足Lipchitz条件，针对生成器，优化函数如式(6)所示.

G_loss=-Ex～pg(x)[D(x)]

(6)

式(6)中：pg(x)为生成样本集合.

针对判别器，优化函数如式(7)所示.

D_loss=Ex～pg(x)[D(x)]-Ex～pdata(x)[D(x)]

(7)

式(7)中：pdata(x)为真实样本集合.

2.2 谱归一化

Miyato等[17]提出谱归一化理论从模型设计角度处理模型存在的缺陷.其主要思想是通过限制模型的参数矩阵保证模型满足Lipchitz条件.对于多层递归神经网络，当输入x时，假设不使用激活函数和偏置b，则输出由式(8)体现.

fn=Wn*Wn-1*…*W1*x

(8)

式(8)中：Wn为第n层网络层的权重矩阵.

其每一层参数矩阵W的谱范数定义如式(9)所示.

σ(W)∶=|max{μ(WWT)}|1

(9)

式(9)中：σ(W)既表示矩阵W的最大奇异值，也为W的谱范数，WT为矩阵W的转置矩阵,μ表示特征矢量.结合式(5)(8)(9)可得.

|Wn|*|Wn-1|*…*|W1|≤

(10)

谱归一化即让参数矩阵除以参数矩阵谱范数，实现参数矩阵归一化目的.同时，参数矩阵数值比例不会被破坏，也满足Lipschitz条件，由式(11)体现.

(11)

式(11)中：fSN(W)为经过谱归一化处理后的权重矩阵.

2.3 注意力块

注意力块类似于残差连接块，分为两条操作路径.主路为注意力机制，辅路为恒等映射.普通卷积操作是通过空间大小固定的卷积核来获取图像上两个像素之间的依赖关系，其关注区域受卷积核大小影响.因此当卷积核尺寸过小时，便难以获取两个相距较远像素之间的联系.注意力机制可以作为普通卷积操作的补充来处理相距较远像素之间的依赖关系[18]，捕获图像更多的细节、纹理信息.注意力机制如图3所示.

图3 注意力机制

由图3可以得到，首先将网络前一层输出的特征图经过两个卷积核为1*1，步长为1的卷积，然后将经过两个卷积得到的输出W1x，W2x(假设不使用偏置b)相乘并经过Softmax归一化得到注意力图，最终将前层输出的特征图与注意力图逐像素点相乘得到自注意力特征图，自注意力特征图求取过程由式(12)体现.

(12)

式(12)中：x为输入的特征图，N=W*H为特征图的像素总数，xi，xj分别为特征图上x第i,j个像素位置.oi为第i个像素的最终输出.经过注意力块的输出特征图如式(13)所示.

fi=oi+xi

(13)

式(13)中：fi为经过注意力块的输出特征图.

2.4 Multi-Loss GAN (MLGAN)模型

Multi-Loss GAN(MLGAN)模型结构由标准的带有生成器，判别器的生成对抗网络(GANs)模型，Vgg19特征提取网络和差异网络三部分构成.MLGAN模型如图4所示.

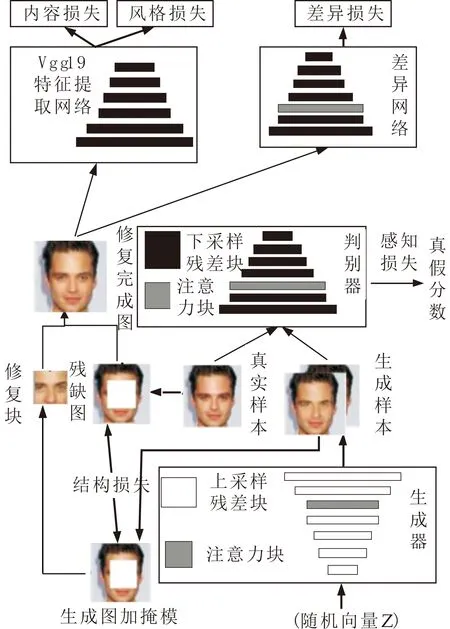
图4 Multi-loss GAN模型结构示意图

2.4.1 生成器

生成器为带有注意力块的解码器网络结构，用于模拟真实图像合成.其不仅决定生成图像的质量，同时决定修复效果是否逼真.生成器由实例归一化层(Instance Norm),激活层(Relu)以及反卷积层(Deconv)构成.考虑到网络提取特征的能力随网络层次加深而增强，同时为了避免网络变深后对网络性能带来的负影响，本文提出上采样残差块结构.上采样残差块由卷积层(Conv)、Relu激活层、实例归一化层、卷积核为3*3，步长为2的反卷积层以及上采样层(upsample)构成.同时，使得网络具备学习图像各像素间相关性的能力，向生成器引入注意力块.如图5所示，左侧为生成器结构简图，右侧为上采样残差块结构图.

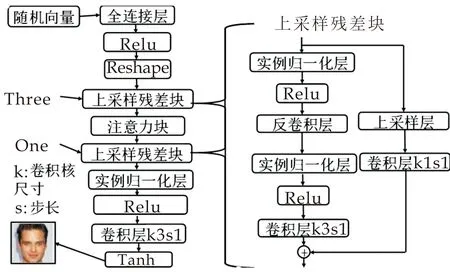
图5 生成器结构图

如2.1节所述，为稳定模型训练，使用式(6)作为生成器的目标函数.

2.4.2 判别器

判别器为带有注意力块的编码器结构，用于判别生成图像的真实程度.判别器由实例归一化层(Instance Norm)、激活层(Leaky_Relu)、卷积层(Conv)构成.考虑到网络提取特征的能力随着网络层次加深而增强，同时为了避免网络变深后对网络性能的负影响，引入下采样残差块结构.下采样残差块结构由实例归一化层、激活层、卷积层、以及下采样层(subsample)构成.同时，使得网络具备学习图像各像素间相关性的能力，向判别器引入注意力块.如图6所示，左侧为判别器结构简图，右侧为下采样残差块结构图.

图6 判别器结构图

如2.1节所述，为稳定模型训练，使用式(7)作为判别器目标函数.

2.4.3 差异网络

差异网络的网络结构等同于判别器的网络结构，用于判别修复完成图的真实程度，在模型修复阶段为模型提供差异损失，向差异网络导入图像生成阶段预先训练好的判别器权重并与基础网络进行拼接，实现网络输出差异损失功能，在模型修复阶段，参数不再更新.差异网络结构如图6所示.差异损失如式(14)所示.

Ld=Ex～pdata(x)[D(x)]-Ex～pblend(x)[D(x)]

(14)

式(14)中：pblend(x)为修复完成样本集合，pdata(x)为真实样本集合.

最小化差异损失，有助于缩小修复完成图与真实图像之间的差异.

2.4.4 Vgg19特征提取网络

Vgg19特征提取网络为编码器结构，用于判别修复完成图是否具备与原图一致的内容、风格特征.使用预先训练好的Vgg19模型与基础网络进行拼接，实现模型的特征提取能力，且在模型修复阶段，Vgg19网络的模型参数不再更新.其网络架构由卷积核为3*3，步长为1的卷积层，池化窗口为2*2，步长为2的池化层，Relu激活层以及全连接层构成.将修复完成图与原始图像输入至Vgg19特征提取网络，提取两者不同级别的特征，计算修复完成图较于原图的内容、风格损失.对于内容损失，将两者在Conv1_1与Conv2_1卷积层提取的特征图进行差异计算；对于风格损失，将两者在Pool2与Pool3池化层提取到的特征图进行差异计算.其中内容损失函数如式(15)所示.

(15)

内容损失用于衡量两幅图像在同一网络层提取到的所有特征图间的差异.最小化内容损失有助于修复完成图的内容特征更逼近于原图.

Gatys等[19]在图像风格迁移领域对网络提取的特征图求解Gram矩阵来定义图像的风格特征，Gram矩阵由网络同一卷积层提取到的所有特征图之间的相似性定义.风格损失函数如式(16)定义.

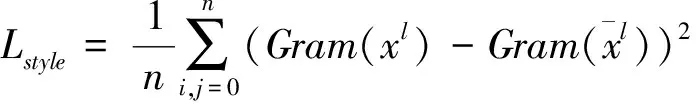
(16)

式(16)中：Gram(xl)表示图像在网络第l层Gram矩阵.

其中风格特征刻画了图像的纹理、颜色等信息，最小化风格损失有助于修复完成图的风格特征更逼近于原图.

2.4.5 总损失函数

为了保证模型修复结果趋于理想，将差异损失项、内容损失项、风格损失项添加至模型修复阶段目标损失函数中，因此，Multi-loss GAN模型在修复阶段损失函数如式(17)所示.

Lall=αLs+βLp+γLd+δLcontent+εLstyle

(17)

式(17)中：α、β、γ、δ、ε为平衡参数，用于平衡各项损失.

3 实验

3.1 数据集预处理与模型训练细节

使用CelebA人脸数据集[20]验证本文方法的有效性.其中CelebA人脸数据集包含202 599张178×218大小的RGB彩色人脸图片，随机将其中80 000张图像用作训练集，10 000张用作验证集，10 000张用作测试集，共使用100 000张，且本次实验的主要目的是恢复人脸特征，因此使用图像剪裁方法去除图片上多余的背景信息避免影响实验结果并调整图片尺寸为64*64以供训练模型.

本次实验的设备条件为Intel(R) Core(TM) i5-8300H CPU，主频为2.30 GHz，内存为16 GB的笔记本电脑和NVIDIA Titan XP GPU，显存为12 GB.同时以PyCharm作为编译器，使用python语言和TensorFlow深度学习框架实现MLGAN模型的搭建.同时，使用Adam优化函数寻找模型的最优解.在图像生成阶段，批样本尺寸为128，生成器和判别器的学习率都为2e-4.模型迭代80 000次后并保存模型参数.在图像修复阶段，通过设置不同的平衡参数得到模型的最终输出，评估模型的最终性能.最终，总损失平衡系数设置如下：α=1，β=3e-3，γ=1e-2，δ=7e-2，ε=1e-3，因为此时模型修复效果最佳，模型的输出结果最优.同时学习率设置为1e-1并迭代2 000步输出最终的修复结果.

3.2 结果

3.2.1 不同模型修复效果对比

本文提出对DCGAN模型增设Vgg19特征提取网络，差异网络形成DCGAN+(DC+)模型.为了验证模型的有效性，将本文的MLGAN模型，DCGAN+模型分别与DCGAN模型、GLCIC模型在CelebA人脸数据集进行实验.图7给出了不同模型在CelebA数据集上的修复结果.本次实验在复现DCGAN模型时，出现模型崩溃问题，因此，对其添加谱归一化和Wasserstein距离稳定模型训练.由图7可以得到，DCGAN模型修复效果较差，图像部分细节特征无法被准确还原；改进后的DCGAN+模型有效还原了部分图像细节；GLCIC模型修复结果较为模糊；MLGAN模型修复效果最佳，但也存在部分细节还原不足.

图7 不同模型修复效果对比图

同时，使用峰值信噪比(PSNR)，结构相似性(SSIM)评估4种模型，具体指标值如表1所示.

表1 不同模型修复效果对比

3.2.2 Multi-loss GAN(MLGAN)性能实验

(1)辅助网络实验

对本文提出的差异网络，Vgg19特征提取网络，设计不同的实验验证网络性能，在相同条件下训练应用不同损失函数的四种模型，每个模型训练70 000次并保存参数.多损失约束模型设计表如表2所示.

表2 多损失约束模型设计表

图8给出了不同模型的修复效果对比.由图8可以得到，Net-D和Net-S模型的修复结果存在图像部分细节特征还原不足问题，Net-C的修复结果存在图像部分纹理结构还原不足问题，Net-All模型修复效果最佳.同时，使用峰值信噪比(PSNR)，结构相似性(SSIM)评估4种模型，具体指标值如表3所示.

图8 多损失约束模型修复效果对比图

表3 多损失约束模型修复效果对比

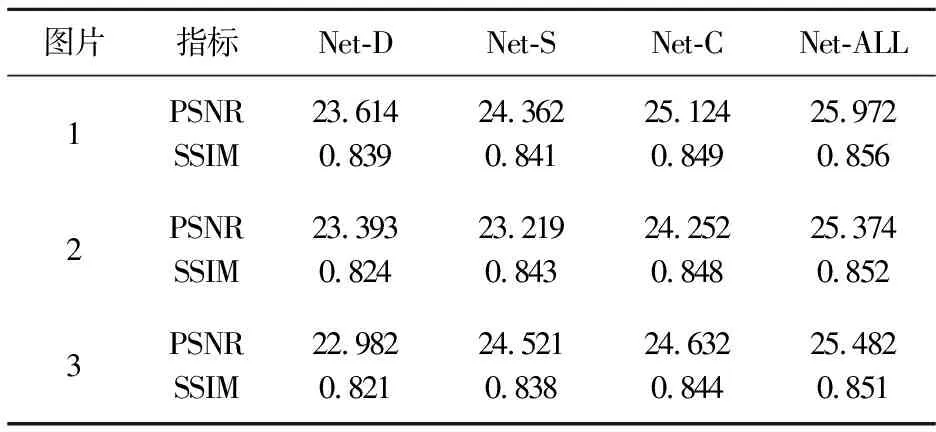
图片指标Net-DNet-SNet-CNet-ALL1PSNRSSIM23.6140.83924.3620.84125.1240.84925.9720.8562PSNRSSIM23.3930.82423.2190.84324.2520.84825.3740.8523PSNRSSIM22.9820.82124.5210.83824.6320.84425.4820.851

(2)注意力块实验

为了验证注意力块对模型性能的影响程度，本文设计引入注意力块(With-Attention,With-A)和不引入注意力块(No-Attention,No-A)两种模型进行测试，每个模型训练70 000次并保存训练参数，具体模型设计表如表4所示.

表4 注意力块性能验证设计表

图9给出了两种模型的可视化比较，可以看到，No-attention模型修复结果存在部分细节特征还原不足问题，With-attention模型修复效果最佳.

图9 不同模型修复效果对比图

同时，使用PSNR、SSIM指标量化两种的修复效果，具体指标值如表5所示.

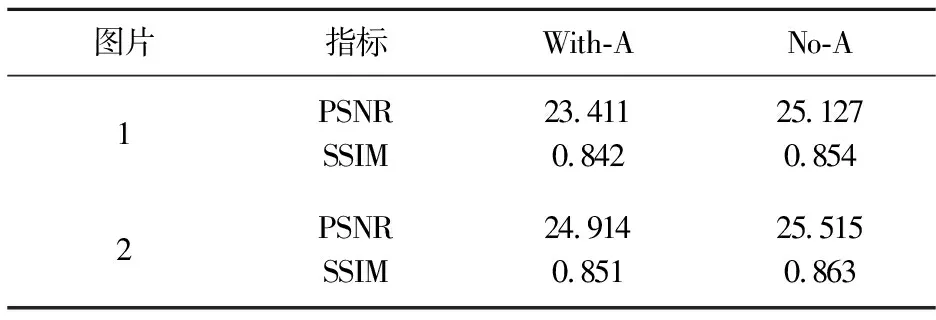
表5 不同模型修复效果对比

3.2.3 不同模型性能实验

为了比较DCGAN和MLGAN在图像生成阶段的模型性能，在相同实验环境下，对每个模型分别训练5 000次、8 000次、12 000次、80 000次后保存模型的生成结果，其中图10展示了DCGAN的生成结果，图11展示了MLGAN的生成结果.可以看到，在第5 000次和8 000次，DCGAN模型的生成结果存在部分细节特征无法被准确生成，图像较为模糊，此时，MLGAN模型的生成结果图像人脸轮廓及细节较为清晰，但也存在部分人脸细节生成不足.在第12 000次时，DCGAN仍存在部分生成图像模糊，特征还原不足问题.在第80 000次，MLGAN整体生成结果轮廓，五官细节较于DCGAN生成结果清晰.由此可见，MLGAN模型拟合图像的能力较于DCGAN更强，收敛速度更快.

图10 DCGAN生成结果图

图11 MLGAN生成结果图

4 结论

为解决基于DCGAN的图像修复模型存在的重建结果特征还原不足问题，提出一种结合残差块和注意力块的Multi-Loss GAN(MLGAN)模型，设计辅助网络提供多损失项协助网络寻找最优编码并引入谱归一化和Wasserstein距离稳定模型训练.从实验结果可以看到，模型从整体上还原出图像缺失信息，提高了修复效果准确性，但存在图像部分细节特征还原不足问题，下一步将针对部分细节特征还原不足问题进行研究.