紫外光谱法水体COD测量的线性-指数分段数学模型
田广军,徐光耀,田 青
1.燕山大学电气工程学院,河北 秦皇岛 066004 2.Department of Electrical and Computer Engineering,McGill University,QC H3A 2A7,Canada
引 言
化学需氧量(chemical oxygen demand,COD)作为衡量水体有机物相对含量的指标,反映了水体受还原性物质污染的程度,是水质监测的一个重要参数指标。目前,国标法检测水质仍以常规化学方法为主,应用也较为广泛,但这类测量方法过程较为复杂,测量时间较长,测量结果不能及时反应水质的变化情况[1-2]。紫外光谱分析法是依据光谱数据对污染物进行定性定量分析的纯物理光学检测方法,相比于常规化学方法,紫外光谱法由于设备结构简单、无二次试剂污染、实时响应速度快、易于实现在线定量分析等优点,得到了广泛关注和深入研究[3-5]。
紫外光谱法利用朗伯-比尔定律分析COD与吸光度关系时常选用邻苯二甲酸氢钾(分子量M为204.22)溶液[7-8],在实际溶液紫外光谱分析中,在朗伯-比尔定律适用范围内达到某浓度值之后,其COD与吸光度明显偏离了线性关系,这一点在许多学者的研究文献中被论及和描述。李玉春在254和280 nm处测量的10~450 mg·L-1COD与吸光度关系曲线中,254 nm的数据在COD大于200 mg·L-1后开始上翘,280 nm的数据在COD大于250 mg·L-1后开始上翘;李家琛[6]在测量25~666 mg·L-1的九种不同浓度邻苯二甲酸氢钾溶液在263和280 nm处的吸光度时,邻苯二甲酸氢钾溶液在225 mg·L-1后的浓度与吸光度关系曲线走势发生明显变化。
为了拓展光谱法溶液浓度测量范围上限,在更宽范围内建立精确的溶液吸光度与COD关系模型,本文研究了COD为40~560 mg·L-1的邻苯二甲酸氢钾溶液的紫外吸收光谱,结合相关系数法、一元鲁棒线性回归和非线性最小二乘回归建立了吸光度-COD的线性-指数分段数学模型,实现了邻苯二甲酸氢钾溶液COD的准确预测。
1 实验部分
1.1 材料与仪器
实验材料选用0.850 2 mg·mL-1邻苯二甲酸氢钾标准溶液(COD值为1 000 mg·L-1)和重蒸水,采用标准溶液稀释步骤配置得到COD值为40~680 mg·L-1的34个不同浓度的溶液样品。激发光源选用Ocean Optics公司的光谱仪专用脉冲氙灯PX-2,具有220~750 nm的稳定连续光谱输出;光谱测量仪器选用Ocean Optics公司的S2000微型光纤光谱仪,其光谱响应范围为200~1 100 nm,光学分辨率为0.3~10 nm FWHM;透射支架选用Ocean Optics公司的CUV-ALL-UV 4-WAY比色皿支架,实验用样品池均为紫外透射率85%以上的10 mm石英玻璃比色皿。
1.2 方法
实验在温度20 ℃(±0.5 ℃)湿度35%(±5%)的暗室中进行,实验系统方框图如图1所示。

图1 实验系统原理方框图Fig.1 Block diagram of experimental system
在光谱实验数据采集前,先将光源打开预热30 min。设置积分时间为10 ms、平均光谱参数为300、Boxcar平滑参数为3,选择暗电流校正。按以下步骤使用OOIBase32光谱软件进行吸收光谱测量:单击工具栏按钮“Scope Mode”,检查并调整光信号强度,使参考光信号的峰值强度为3 500 counts;单击工具栏上的“Store Reference Spectrum”按钮,将当前参考光谱记录到计算机光谱实验文件;遮挡光路并单击“Store Dark Spectrum”按钮,保存实验系统的暗电流光谱文件以备暗电流校正用;将样品放置在比色皿支架中,单击“Absorbance Mode”按钮进入吸光度测量模式,单击“Save”按钮并选择文件路径后,将吸收光谱保存到计算机磁盘进行分析处理。
2 结果与讨论
分别配置COD值为40,80,160,180,190,200,210,220,240,260,280,300,320,340,360,380,400,440,480,520,560,600,640和680 mg·L-1的24份样品作为校正集,通过对校正集样品和邻苯二甲酸氢钾标准溶液原液的紫外吸收光谱扫描,得到了较宽浓度范围的校正集样品COD-吸光度紫外吸收光谱,如图2所示。利用光谱仪系统软件内置的平滑滤波功能,结合光谱观察分析,除选取暗电流校正外,还设置了适当大的时间窗口和波长窗口参数,省去了附加滤波,避免了实验室条件下对原始数据的过度预处理。
从图2可见,样品的吸光度有明显的波长选择性,即样品在220~300 nm之间有明显的吸收特性,样品的吸光度在320 nm之后几乎为零。样品紫外吸收光谱存在两个较大的特征峰,第一个特征峰在233 nm左右,但随着样品COD浓度的增大,第一个特征峰发生红移,向着第二个特征峰的方向逐渐偏移和靠拢,第二个特征峰的位置相对固定为275 nm。

图2 校正集样品COD-紫外吸收光谱图Fig.2 COD-UV absorption spectra of samples in calibration set
2.1 选取优势波长
通过相关系数法计算样品COD与吸光度两个向量之间关系的相关程度。相关系数R由式(1)计算
(1)

用Matlab软件编程计算出样品COD值与吸光度的相关系数随波长变化曲线如图3所示。
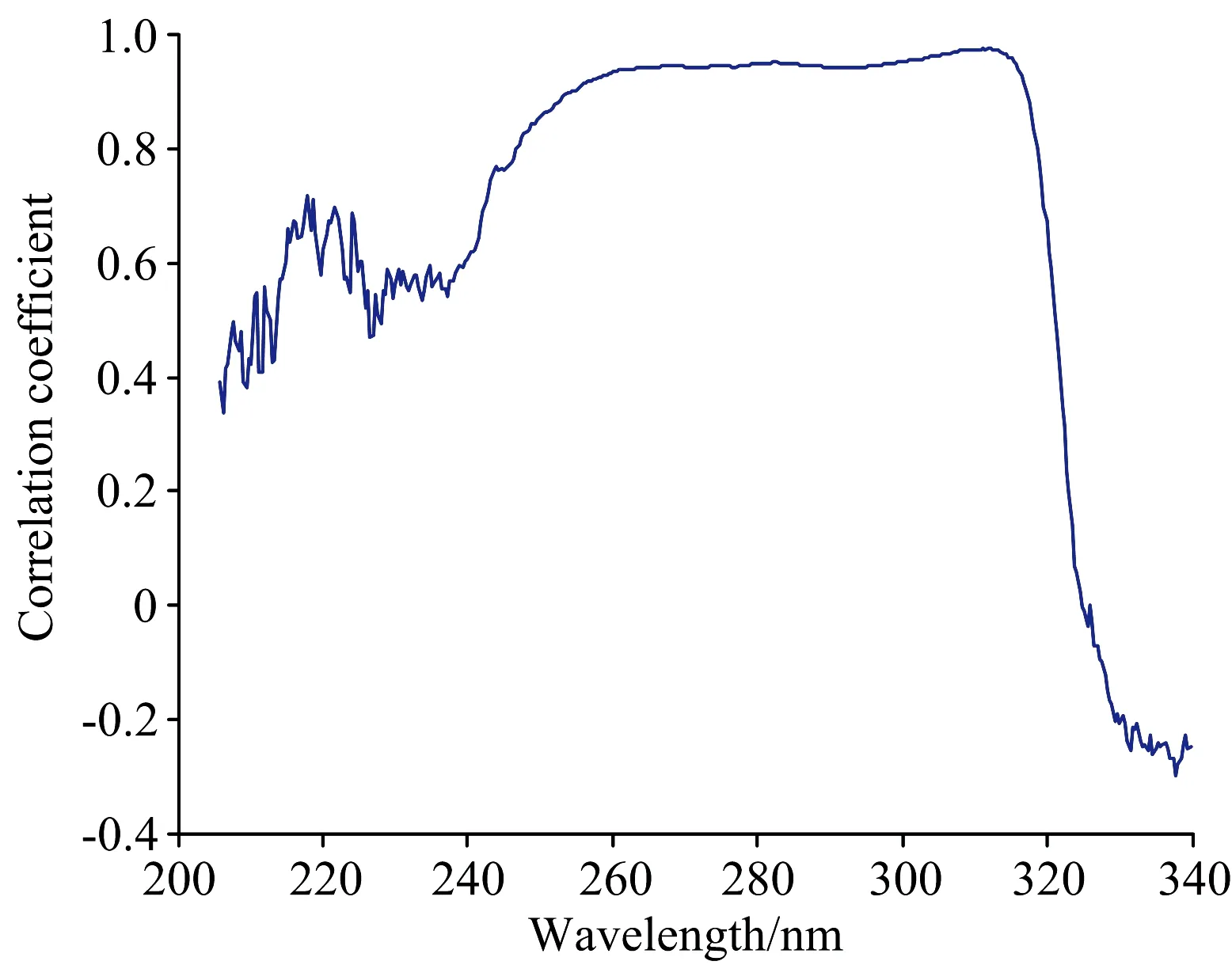
图3 样品COD与吸光度的相关系数随波长变化曲线Fig.3 Correlation coefficient between absorbance and COD of sample
由图3可见,样品COD与吸光度的相关系数是随波长变化的。对比图2与图3的波长变化范围可知,虽然相关系数的变化波段比吸光度的变化波段有所扩展,但可测范围主要还是在220~300 nm之间。由于相关系数最大时的波长超出了图2中的吸收范围,选择相关系数大于0.8的波段为优势波段,对应的波长范围为251.35~319.91 nm。由于第一个特征峰的红移现象,峰值波长不固定,且低浓度时第一个特征峰不在优势波段范围内,所以选择第二个特征峰275 nm作为备选优势波长。
由于紫外吸收光谱法常用254和280 nm分析水质COD[7-8],对比254,275和280 nm三处COD-吸光度数据走势如图4所示,同一样品在不同波长下吸光度不同,但是随着样品浓度增加,三个波长下数据变化趋势基本相同,低浓度阶段符合朗伯-比尔定律,浓度较高时样品COD与吸光度会偏离正比例关系,呈现类指数规律变化,由于275 nm波长对应的关系曲线具有较好的吸光度动态特性,所以选用实验所测的第二个特征峰波长275 nm作为优势波长进行分析。
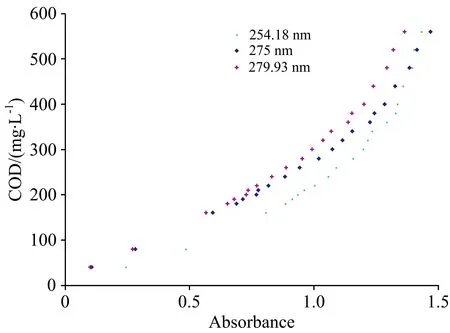
图4 254.18,275和279.93nm波长的COD-吸光度曲线走势对比Fig.4 Trend comparison of COD-absorbance data at 254.18,275 and 279.93 nm
2.2 建立线性-指数分段回归模型
本文利用一元鲁棒线性回归方法建立低浓度段COD与吸光度关系的数学模型,对较高浓度段采用一元非线性最小二乘回归方法。回归算法分别采用Matlab工具箱中的robustfit函数和nlinfit函数。基于理论和实验分析,验证浓度较低时COD与吸光度成正比例关系,符合朗伯-比尔定律;确定浓度较高时吸光度与COD呈现的指数关系。
首先,计算各拟合模型对各假设模型临界点的下一个数据点的预测相对误差R,以R连续三次大于5%或小于-5%为判断条件,取第一次符合判断条件时对应的假设模型临界点为分段点,然后根据所确定的模型临界点对各段数据进行分段回归以获得更精确的模型。
2.2.1 低浓度段模型
以COD值40 mg·L-1为起点、190~300 mg·L-1的8个数据点为假设模型临界点分别进行一元鲁棒线性回归,得到各个回归模型的均方根误差RMSE、对下一个数据点的预测COD、预测相对误差R等参数如表1所示。
由表1可见,假设模型临界点为300 mg·L-1之后的预测相对误差R均小于-5%,且偏差越来越大,即低浓度段中,COD大于300 mg·L-1之后的溶液吸光度与COD关系,已经不再符合线性回归方程。所以,选择COD为300 mg·L-1的数据点为低浓度段数据模型临界点。
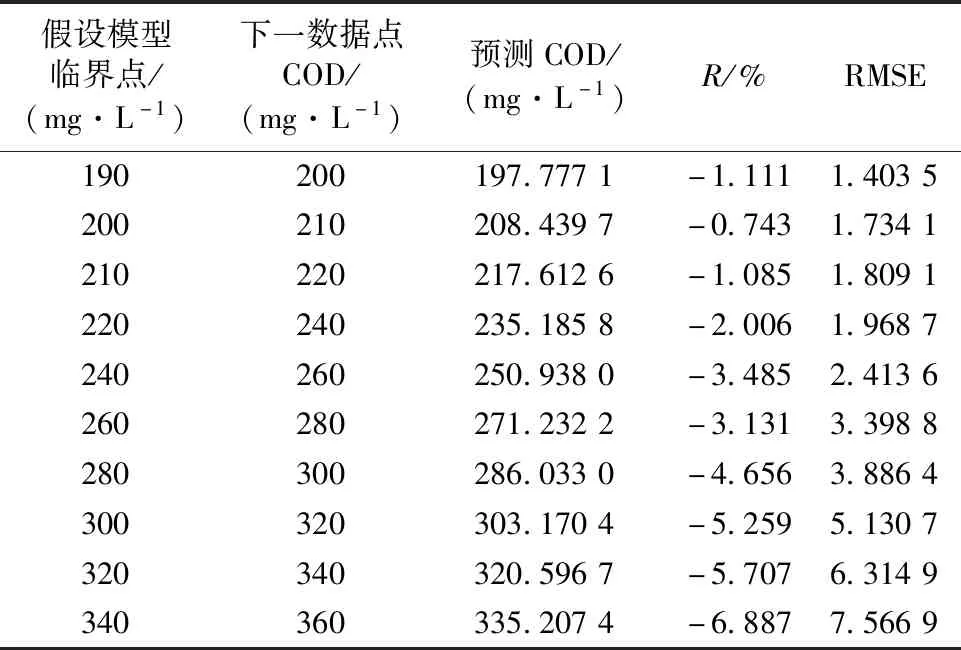
表1 各模型临界点的回归方程参数Table 1 Regression equation parameters of critical point for each model
在波长275 nm处对COD为40~300 mg·L-1的数据建立一元鲁棒线性回归模型,得到样品COD值y和吸光度x关系的回归方程为
y=0.524 4+271.431 4x
(2)
回归方程曲线如图5所示,用均方根误差作为评价指标,校正模型的均方根误差为5.130 7,对预测集的均方根误差5.158 3。

图5 低浓度段样品COD-吸光度关系回归曲线Fig.5 Regression curve of sample COD and its absorbance in low concentration range
2.2.2 较高浓度段模型
以COD值300 mg·L-1为起点、480~600 mg·L-1的4个数据点为假设模型临界点分别进行一元非线性最小二乘回归,得到各个回归模型的均方根误差RMSE、对下一个数据点的预测COD、预测相对误差R等参数如表2所示。
由表2可见,假设模型临界点为560 mg·L-1之后的预测相对误差R均小于-5%,且偏差越来越大,即较高农度段中,用COD大于560 mg·L-1之后的数据点进行一元非线性最小二乘回归的回归方程精度不理想,数据点再次发生偏离。所以,选择COD为560 mg·L-1时的数据点为较高浓度段数据模型临界点。

表2 各模型临界点的回归方程参数Table 2 Regression equation parameters of critical point for each model
在波长275 nm处对COD为300~560 mg·L-1的数据建立一元非线性最小二乘回归模型,得到样品COD值y和吸光度x关系的回归方程为
y=2.182 5e1.595 2x+3.192 1
(3)
回归方程曲线如图6所示,用均方根误差作为评价指标,校正模型的均方根误差为7.117 5,对预测集的均方根误差7.856 3。
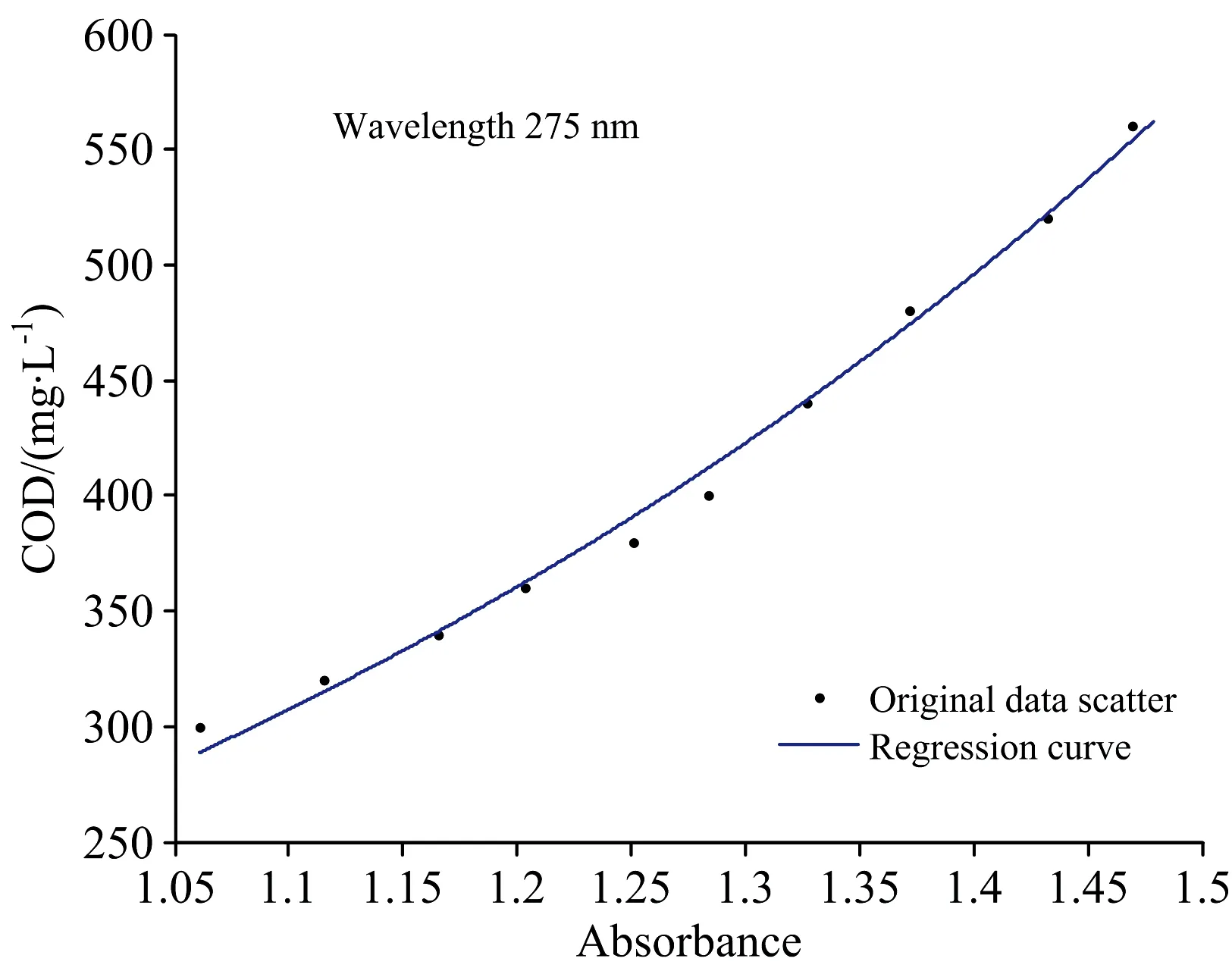
图6 较高浓度段样品COD-吸光度关系回归曲线Fig.6 Regression curve of sample COD and its absorbance in higher concentration range
令式(2)和式(3)相等,得到最终模型转折点的COD值y=288.350 3,吸光度x=1.060 4,则获得40~560 mg·L-1段样品COD-吸光度关系的回归曲线如图7所示。
同时,由表2可见,在模型临界点560 mg·L-1后所建立的回归方程对下一个数据点COD的预测误差越来越大,进一步分析COD-吸光度数据变化趋势可知,275 nm处COD为560~1 000 mg·L-1的邻苯二甲酸氢钾溶液的吸光度为1.469~1.535,只增大了0.066,溶液浓度过高导致溶液吸光度接近饱和。
2.3 模型拟合精度对比
对校正集样品在COD值为300~560,40~560以及40~560 mg·L-1的全范围内分别进行紫外吸收光谱的数据一元鲁棒线性回归和一元非线性最小二乘回归,计算回归模型的均方根误差,得到各个模型拟合精度如表3所示,其中RMSE是校正集均方根误差。
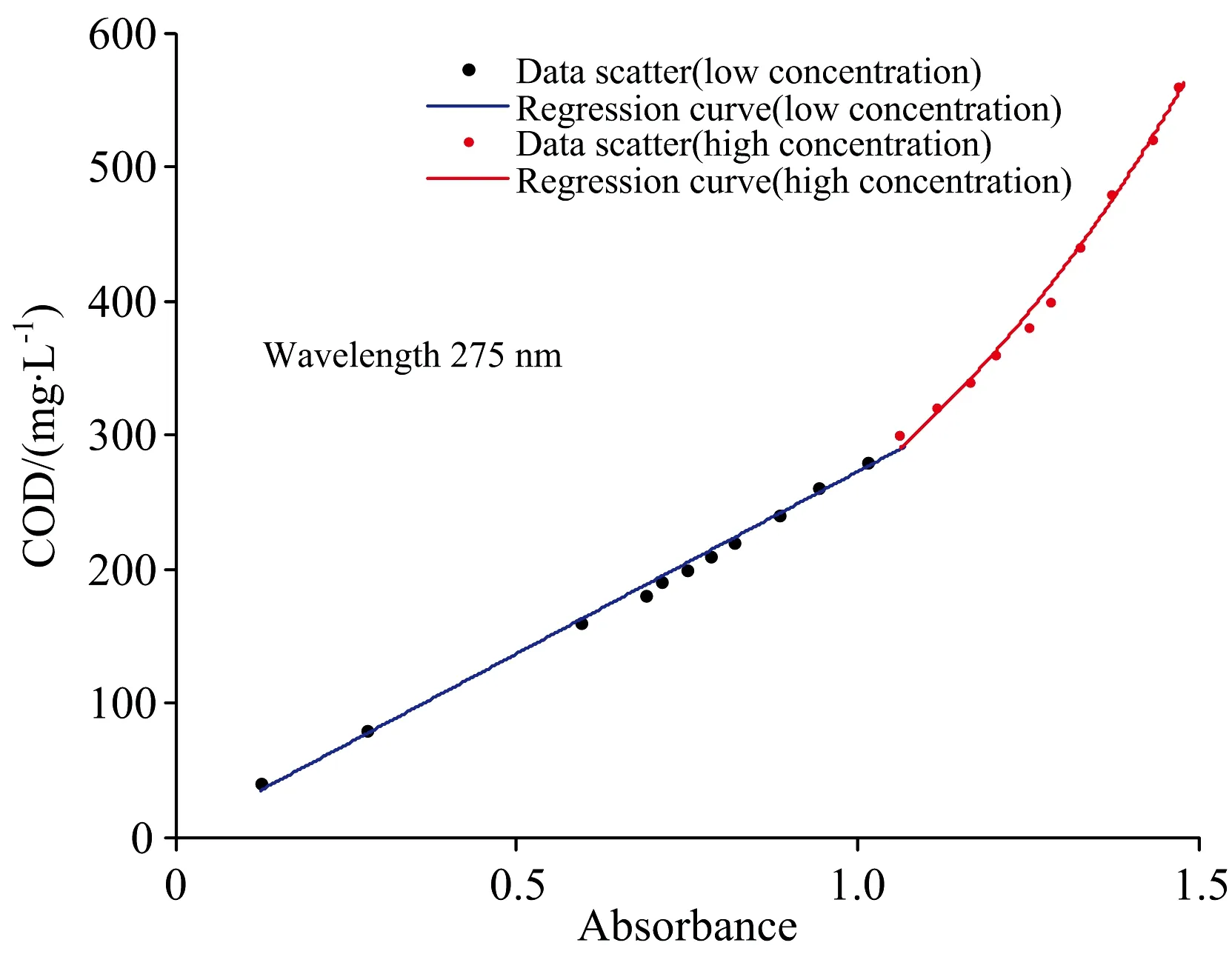
图7 样品COD-吸光度关系分段回归曲线Fig.7 Regression curve of absorbance and COD

表3 不同模型的拟合精度Table 3 Fitting accuracys of each model
由表3可知,对全浓度段校正集样品紫外吸收光谱数据建模时,线性模型性能很差,RMSE达到了41.175 0;非线性模型性能也不好,其拟合数据在低浓度段时的RMSE达到了10.085 8,约为线性-指数分段模型的两倍,所以不能直接使用非线性模型对水体COD进行测定。对较高浓度段校正集样品紫外吸收光谱数据建模时,线性模型的性能依然不好,RMSE达到了14.109 8,为线性-指数分段模型的两倍多,所以也不能采取两段线性模型对水体COD进行测定。线性-指数分段模型的拟合精度最高。
2.4 线性-指数分段模型预测效果
重新配置COD值为40~560 mg·L-1的31份样品作为预测集,用所建线性-指数分段模型对预测集样品的预测数据如表4所示,预测效果如图8所示。
用均方根误差作为评价指标,所得测量模型对预测集样本的预测效果如表5所示,其中RMSE是校正模型的均方根误差,RMSEP是预测均方根误差。
由表5可见,所建线性-指数分段模型对预测集275 nm处COD范围为40~560 mg·L-1的溶液的预测效果较好,预测均方根误差仅为5.664 7。

表4 预测集各样品对应的预测数据Table 4 Predictive data corresponding to the prediction set of each sample
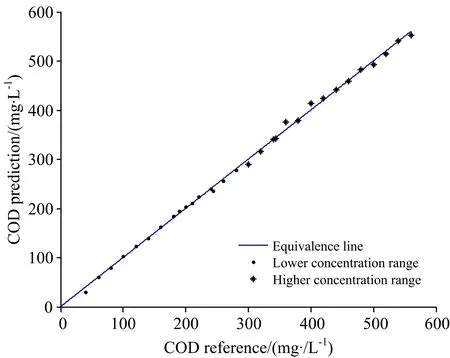
图8 模型预测效果图Fig.8 Prediction effect diagram

表5 测量模型预测效果Table 5 Prediction effect of model
3 结 论
邻苯二甲酸氢钾溶液的紫外吸收光谱实验结果分析表明,当溶液浓度增大到一定程度时,吸光度与COD值会明显偏离线性关系,低浓度段吸光度-COD关系模型的临界点位于COD值300 mg·L-1附近,此临界点之后的吸光度-COD关系已经不再符合朗伯-比尔定律,在300~560 mg·L-1较高浓度范围内COD与吸光度的关系呈指数变化规律。模型变化的内在机理及转折点的影响因素有待进一步探讨。本工作所建线性-指数分段测定模型对预测集样品的预测均方根误差仅为5.664 7,预测效果较好。线性-指数分段数学模型的建立,提高了溶液COD紫外光谱测量方法的泛化能力,对于具有较高COD浓度的水体质量参数测量提供了可行性实验及理论依据。

