范畴中的拟-morphic对象
陆二伟,储茂权,姜翠翠
(1.安徽师范大学 数学与计算机科学学院,安徽 芜湖 241003;2.定远县第三中学,安徽 定远 233200)
2005年,Nicholson等在模范畴中引入了模。2006年,颜晓光等给出G-morphic模的定义[1]。2009年,邢宝国等提出了拟-morphic模的概念[2]。2012年,时芳芳等给出拟G-morphic模的定义[3]。2013年,Calugareanu等结合范畴及morphic模的概念给出了范畴中morphic对象的定义[4],研究morphic对象在范畴中的一些性质,并考虑了单位正则元,正则元与morphic元间的联系。
1 预备知识
文中出现的环均是有单位元的结合环,环上的模均指酉模,未定义的符号可参见文[5]。
定义1[5]设有零对象范畴C中对一切A,B∈ObC,HomC(A,B)∈ObAG(对加法)且态射合成与加法满足分配律,即在可合成与可加情况下,有则称C为预加法范畴。
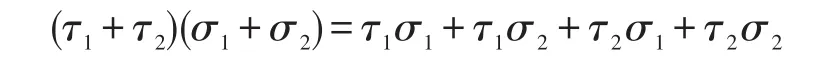
定义2[5]设C为预加法范畴,若C的任何有限个对象A1,A2,…,An都有直和,则称C为加法范畴。
定义3[5]设C为加法范畴,若C又满足下述各条件:
(1)C中任何态射都有核和上核;
(2)C中任何单态射都是其上核的核,任何满态射都是其核的上核;
(3)C中任何态射σ都可分解成一个单态射η和一个满态射π之积:σ=ηπ,此式称为σ的标准分解式,则称C为一个Abelian范畴。
Abelian范畴⇒加法范畴⇒预加法范畴⇒带零范畴。左R-模范畴RM和Abelian群范畴AG均是Abelian范畴。
定义4[6]称带零范畴C是p-exact的,若C中每个态射可以分解为正规的单态射和上正规的满态射之积。
定义5[6]称范畴中的单态射f是正规的,若f是某个态射的核。
定义6[6]称范畴中的满态射g是上正规的,若g是某个态射的上核。
Abelian范畴是p-exact范畴,但反之不一定成立。在p-exact范畴中,核和上核存在,每个单态射均是正规的且每个满态射均是上正规的。单态射沿任意态射可以拉回,满态射沿任意态射可以推出。但是积、和、一般的拉回及推出不一定存在。众所周知,p-exact范畴是Abelian的当且仅当存在有限和。左R-模范畴RM和AG是Abelian范畴,当然也是p-exact的。但群范畴G和环范畴Ring均不是p-exact的(见文[7])。
定义7[8]设M是范畴C中一簇单态射,A,B∈ObC,如果存在M中的一个态射f:A→B,则称(A,f)为对象B的M子对象。若M是C中的全体单态射,则简称(A,f)为对象的子对象。
在群范畴、Abelian群范畴和左R-模范畴RM中,子对象分别对应于子群、子Abelian群和子R-模。
2 p-exact范畴中的拟-morphic对象
设A是有核和像的范畴C中的对象,称A的自态射α是morphic的,若存在β∈EndC(A),使得下面序列正合
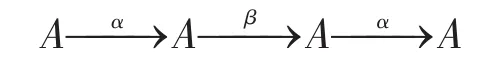
称对象A是morphic,若对任意的α∈EndC(A),α是morphic的。结合拟-morphic模的定义(称左R-模M是拟 -morphic的[9],若对任意的α∈EndR(M)),存在β,γ∈EndR(M) ,使得Mα=Ker(β)和 Ker(α)=M(γ),可以定义有核和像范畴C中-morphic的拟对象。
定义8设A是有核和像的范畴C中的对象,称A的自态射α是拟-morphic的,若存在β,γ∈EndC(A),使得下面序列正合

称对象A是拟-morphic的,若对任意的α∈EndC(A),α是拟-morphic的。
A的自态射α是拟-morphic的当且仅当存在α,β∈End(A) ,使得Imα=Ker(β) 且 Ker(α)=Imγ。显然,若α是-morphic的,则α是拟-morphic的(由正合,可得正合),反之不一定(见[10]的命题5)。
例1(1)设R是有单位元的环,左R-模范畴RM中的拟-morphic对象即拟-morphic模(见文[11])。
(2)由morphic Abelian群是拟-morphic的,故在Abelian群范畴AG中,拟-morphic对象包括morphic Abelian群,关于morphic Abelian群的更多性质见文[12]。
注:(1)每个自同构σ:A→A是拟-morphic的(取β=λ=0),事实上,恒等态射和零态射是拟-morphic的,故零对象是拟-morphic的。
(2)拟-morphic对象的子对象不一定是拟-morphic的。例如Z-模zQ是拟-morphic的,但子模zZ不是拟-morphic的。
(3)拟[-morphic]对象的商不一定是拟-morphic的。例如,平凡扩张R=Z∝Q/Z是拟-morphic的,但R/J(R)≅Z不是拟-morphic的(见文[13])。
(4)拟-morphic自态射的合成与和不一定是拟-morphic的。例如,左Z-模范畴ZM中对象M=Z⊕Z12,自态射α,β分别为:α((x,y))=(3x,y),β((x,y))=(6x,y)。易证,α,β均是拟 -morphic的,但αβ和α+β均不是拟-morphic的(见文[14])。
下面给出在p-exact范畴中,拟-morphic自态射的一些性质。
引理1设A是p-exact范畴C中的对象,α∈EndC(A),则下列命题等价:
(1)α是拟-morphic的;
(2)A/Imα可嵌入到A中,且 Ker(α)是A的像。
证明(1)⇒(2)设α是拟-morphic的,则存在β,γ∈EndC(A)使得下面序列正合

故 Imα=Ker(β),Ker(α)=Imγ。显然,Ker(α)是A的像。由 Imα=Ker(β),知A/Imα=A/Ker(β)≅Imβ⊆A。从而A/Imα可嵌入到A中。
(2)⇒(1)由于A/Imα可嵌入到A中,则定义单态射σ:A/Imα→A,态射β:A→A;a→σ((a+Imα)),∀a∈A,则 Imα=Ker(β)。由 Ker(α)是A的 像 ,不 妨 设 Ker(α)=Imγ,其中γ∈EndC(A),故α是拟-morphic的。
定理1设A是有核和像的范畴C中的对象,α∈EndC(A)是拟-morphic的,若σ:A→A是自同构,则ασ和σα均是拟-morphic的。
证明α∈EndC(A)是拟-morphic的,
则 存在β,γ∈EndC(A),使得 Imα=Ker(β),且Ker(α)=Imγ。
由于σ:A→A是自同构有A/Im(ασ)≅A/Imα=A/Ker(β) ≅ Imβ≅A,且 Ker(ασ)=Ker(α)=Imγ是A的像。利用引理1知,ασ是拟-morphic的。类似可证σα是拟-morphic的。
称自态射α:A→A是单位正则的[4],若存在的自同构σ使得α=ασα。等价地,称自态射α:A→A是单位正则的,若α=πσ,其中π2=π,σ是自同构。事实上,单位正则的自态射是拟-morphic的。
定理2设A是有核和像的范畴C中的对象,α,β∈EndC(A)是拟 -morphic的,若α满,β单,则βα是拟-morphic的。
证明由于α,β∈EndC(A)是拟-morphic的,则 存 在λ,ρ∈EndC(A) 使 得 Ker(α)=Imγ,Imβ=Ker(ρ)。又因为若α满,β单,故 Ker(βα)=Ker(α)=Imγ且 Im(βα)=Imβ=Ker(ρ) 。 从而βα是 拟-morphic的。
首先在ρ-exact范畴中,对于短正合列通常在同构意义下,把C记 为B/A。 因 此 ,对 于,若是(上)像的单满分解,则正合,根据第一同构定理有,A/Ker(α)≅Imα。其次,对于p-exact范畴中的态射f:A→B,有f单当且仅当Ker(f)=0;f满当且仅当Imf=B(见文[4])
推论1设A是p-exact范畴C中的对象,α∈EndC(A)且α是拟-morphic的,即存在A的自态射β和γ,使正合。则(1)α单⇔γ为零态射;(2)α满⇔β为零态射。
证明由于正合,则αγ=0 ,βα=0 ,Imα=Ker(β)且 Ker(α)=Imγ。
(1)设α单,由αγ=0=α0,利用α左可消得γ=0 。反之,设γ为零态射,则Ker(α)=Imγ=0 ,故α单。
(2)设α满,则α=1Aα是α的单满分解。故Ker(β)=A,即β为零态射。反之,设β为零态射,则Imα=Ker(β),故α满。
下面利用子对象给出拟-morphic对象的一些等价刻画。
命题1设A是p-exact范畴C中的对象,则下列命题等价:
(1)A是拟-morphic的;
(2)若A/K≅N,其中K和N为A的子对象,则存在A的子对象T和H,使得A/T≅K和A/N≅H。
证明(1)⇒(2)设(K,μ)为拟-morphic对象A的子对象,记A/K=(CoKer(μ),ρ)(在同构的意义下),即有短正合列
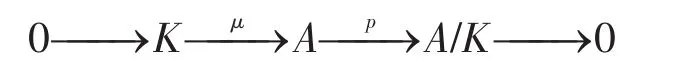
若(N,υ)是A的另一个子对象,则有相应的短正合列
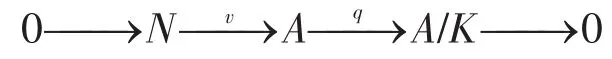
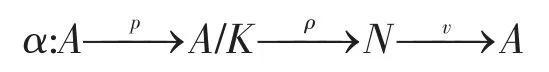
显然,此式α=vρp为α的单-满分解。则Ker(α)=K,Imα=N。由A是拟 -morphic的,对于A的自态射α,存在β,γ∈EndC(A)且,使得Ker(β)=Imα=N,且 Imγ=Ker(α)=K,对β,γ利用第一同构定理得A/Ker(β)≅Imβ,A/Ker(γ)≅Imγ=K。记T=Ker(γ),H=Imβ。
(2)⇒(1)对于任意的α∈EndC(A),有A/Ker(α)≅Imα。由假设知,存在A的子对象(T,f)和 (H,g)使得A/T≅Ker(α)和A/Imα≅H。同上,则有短正合列
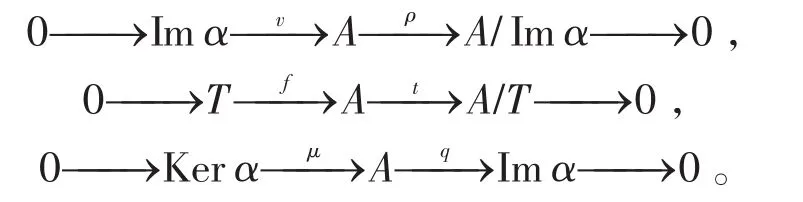
考虑
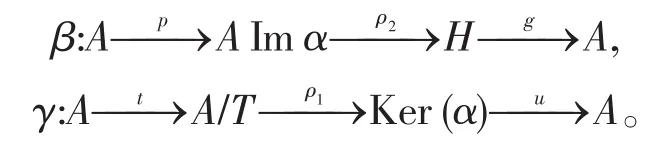
则 Ker(β)=Imα,Imγ=Ker(α) 。 因此α是拟-morphic的。由的任意性知,A是拟-morphic的。
定理3设A是p-exact范畴C中的拟-morphic对象,则下列命题等价:
(1)A的任一子对象均同构于A的一个像;
(2)A的任一像均同构于A的任一子对象。
证明(1)⇒(2)对于A的任一子对象N,由(1)知,存在着子对象K,使得A/K≅N。由于A是拟-morphic的,利用定理2,则存在着子对象H使得A/N≅H。
(2)⇒(1)对于A的任一子对象K,由(2)知存在着子对象N,使得A/N≅H。由于A是拟-morphic的,则存在着子对象T使得A/T≅K。
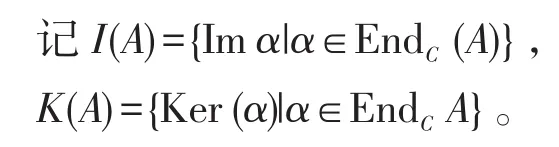
定理4设A是p-exact范畴C中的对象,则A是拟-morphic的⇔I(A)=K(A)。
证明(⇒)设A是拟-morphic的,对于任意的 Imα∈I(A),由α是-morphic的,则存在β∈EndC(A) ,使得Imα=Ker(β) 。 因此Imα∈K(A),I(A)⊆K(A)。若 Ker(α)=Imγ。因此K(A)⊆I(A)。故有I(A)=K(A)。
(⇐)对任意的α∈EndC(A),有 Imα∈I(A)=K(A),则存在β∈EndC(A),使得 Imα=Ker(β)。同理,Ker(α)∈K(A)=I(A)。故存在γ∈EndC(A),使得 Ker(α)=Imγ。从而,α是拟 -morphic的。由α的任意性知,A是拟-morphic的。
称群G是单系列的[6],若它的正规子群格构成有限长度的链,即有G=G0⊃G1⊃G2⊃…⊃Gn=1,并记Gk的长度为IG(Gk)=n-k,其中k=0,1,…,n。称模M是单系列的[15],若它的子模格是链。类似地,称范畴中的对象是单系列的[16],若它的子对象构成链。若对象A的子对象构成有限长度的链:A=A0⊃A1⊃A2⊃…⊃An=0,同样地,我们可以定义子对象记Ak的长度为lA(Ak)=n-k,其中k=0,1,…,n。
引理2设p-exact范畴C中的对象A是单系列的且lA(A)=n,即子对象A=A0⊃A1⊃A2⊃…⊃An=0,则
(1)若A的子对象H是单系列的,则lA(H)=lH(H);
(2)若Ai≅A/Ak,则i=n-k。
定理5设p-exact范畴C中的对象A是单系列的且lA(A)=n,即子对象A=A0⊃A1⊃A2⊃…⊃An=0,则下列命题等价:
(1)A是拟-morphic的;
(2)若A/Ak≅An-k,k=0,1,…,n,则A/An-k≅Ak;
(3)A是-morphic的。
证明(1)⇒(2)若A/Ak≅An-k,k=0,1,…,n,由于A是拟 -morphic的,则存在N=Ai,使得A/An-k≅Ak。由引理2知,i=k。故A/An-k≅Ak。
(2)⇒ (3)设α∈EndC(A),记 Ker(α)=Ak,Imα=Ai,则A/Ak≅Ai,由引理 2 知,i=n-k。再利用(2),有A/An-k≅Ak,即A/Imα≅Ker(α),从而A是morphic的。
(3)⇒(1)显然。
注意到这部分结果没有涉及加法结构(即Hom(-,-)态射集不具有加法群结构),当然也没有有限积。
3 Abelian范畴中的拟-morphic对象
研究Abelian范畴中的拟-morphic对象的有限直和。首先,下面两个定理有助于将研究简化到模范畴中。
定理6[17]设C是Abelian范畴A的小子范畴,则存在A的小Abelian全子范畴D,使得C是D的子范畴。
定理7[17](Mitchell Theorem)设C是小Abelian范畴,则存在环R和完全忠实正合函子

定理8设C和D是Abelian范畴,F:C→D是完全忠实正合函子,且A∈ObC,则A是拟-morphic的⇔F(A)是拟-morphic的。
证明(⇒) 设A是拟-morphic的,为F(A)的自态射。由于F是完全的,则存在α∈EndC(A),使得=F(α)。 又因为A是拟-morphic的,则存在β,γ∈EndC(A),使得下面序列正合

由F正合,可知
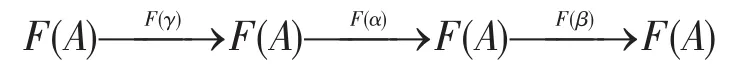
正合。从而F(A)是拟-morphic的。
(⇐)若F(A)是拟-morphic的,且α∈EndC(A),则存在使得

正合。由于F是完全的,则存在β,γ∈EndC(A),使得。故
正合。又因为F正合忠实的(见[18]定理7.1),有
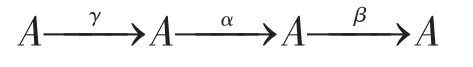
从而A是拟-morphic的。
命题2设A=A1×A2×…×An,Ai为Abelian范畴C中的对象(i=1,2,…,n)且满足i≠j时,HomC(Ai,Aj)=0,则A是拟-morphic的 ⇔Ai是拟-morphic的 (i=1,2,…n)。
此命题在模范范畴条件下的证明已在文[14]中给出。
定理9设A为Abelian范畴C中的拟-morphic对象,则
(1)有限个A的像的交仍是A的像;
(2)有限个A的像的和仍是A的像。
推论2设A为Abelian范畴C中的拟-morphic对象,则I(A)和K(A)均是格。
称范畴C中的对象是正规的[4],若EndC(A)是正则环。记αA为α的像。
引理2[17]设A为Abelian范畴C中的对象,α∈EndC(A),则α是正则的⇔αA和Ker(α)均是A的直和项。
设A为范畴C中的对象,称A是自投射的,若γA⊆αA,其中α,γ∈E=EndC(A),则γ∈αE;称A生成核,若对于任意的β∈E=EndC(A),A生成Ker(β),即 Ker(β)=∑{αA|α∈ EndC(A)}。
命题3设A为Abelian范畴C中的对象,若E=EndC(A)正则,则A是拟-morphic的,自投射的且A生成核。
证明对于任意的α∈E,由于E正则,故存在β∈E使得α=αβα。首先证明αA⊆Ker(1-αβ)。对任意的x∈Ker(1-αβ),即(1-αβ)(x)=0,从而x=(αβ)(x)∈αA,故Ker(1-αβ)⊆αA。
下 证 Ker(α)=(1-βα)A。 由α=αβα知,α(1-βα)=0 ,则α(1-βα)A=0 ,从而 (1-βα)A⊆Ker(α)。对任意的y∈Ker(α),即α(y)=0 ,从而y=y-(βα)(y)=(1-βα)(y)∈(1-βα)A。故 Ker(α)⊆(1-βα)A。
综上可知,则α是拟-morphic的。由α的任意性可知,A是拟-morphic的。
由E正则知,E是右拟-morphic环。设γA⊆αE,其中γ,α∈E,lE(α)⊆lE(γ)。再利用文[10]得,E是左p-内射的,从而γE⊆αE,有γ∈αE,可知A是自投射的。
对于任意的β∈E,由于A是拟-morphic的,则存在λ∈E,使得λA=Ker(β),这就证得A生成核。
设A为 AbelianC中的对象,称A是的kernel-direct[4],若对任意的a∈EndC(A),Ker(α)是A的直和项;称A是image-direct[4],若对任意的a∈EndC(A),Imα是A的直和项。对于拟-morphic对象,kernel-direct能推 出image-direct,反之亦然。因此,有下面结论。
定理10设A为AbelianC中的对象,E=EndC(A),则下列命题等价:
(1)E正则;
(2)A是拟-morphic的且kernel-direct;
(3)A是拟-morphic的且。
4 小结
本文在有核和像的范畴中引进拟-morphic对象的概念,给出了拟-morphic对象的一些等价刻画,并讨论了拟-morphic元与单位正则元以及正则元的关系,并研究了拟-morphic对象在p-exact范畴和Abelian范畴中的一些性质。得到两个主要结果即文中的定理3和定理8。这说明范畴中的拟-morphic对象是morphic对象的真正推广。

