大跨度悬索桥地震响应影响因素统计分析
刘军泉
(兰州铁道设计院有限公司,甘肃 兰州 730030)
统计显示,全球每年平均发生18次破坏性地震,并造成约1万人死亡,每年造成的直接经济损失和救灾费用多达数十亿美元[1]。据我国地震台网中心统计,全球强震主要集中活动在环太平洋地震带和亚欧地震带[2],而我国恰好位于以上两个地震带之间,近年来我国震害频繁。而桥梁作为现代社会的交通枢纽工程,因地震破坏后很难修复,这不但会造成生命财产损失,更会中断交通影响震后救援效率。
悬索桥作为一种优良的大跨度桥型,其抗震设计问题一直是国内外学者关注的重点和难点。行波效应方面:Abdel-Ghaffar等[3]得到行波效应对金门大桥的地震反应影响显著;胡世德等[4]发现多点激励对桥梁结构影响较小,行波效应会加大桥梁结构的地震波反应。激励振型方面,胥润东[5]针对琼州海峡超大多主跨公铁两用悬索桥结构方案进行了一致和非一致地震激励下的时程反应分析;陈水生等[6]分析了多维多点地震激励下视波速及地震非平稳性对结构随机地震响应的影响;Adanur等[7]通过随机振动方法分析了悬索桥在多点地震激励下的响应特征;邓育林等[8]结合2座大跨度悬索桥工程实例探讨了高阶振型对大跨度悬索桥地震反应的影响。结构构件方面:徐勋等[9]建立某大跨钢桁架加劲梁悬索桥的3种中央扣模式的空间动力计算模型,对其动力特性和在地震激励下的时程反应进行空间非线性分析;彭益华等[10]分析了中央扣和加劲梁端弹性连接刚度对其地震反应的影响;代希华等[11]研究了大跨度悬索桥地震响应中的缆索应力刚化效应和结构大位移效应;Apaydin[12]对土耳其2座悬索桥进行了地震性能评价,探讨了滞迟阻尼器进行减震控制的可行性;Kim等[13]研究了悬索桥的非线性弹塑性动力分析方法;苏成等[14]分析了设有非线性粘滞阻尼器的悬索桥地震响应;其他方面:聂利英等[15]探讨了几何非线性对大跨度悬索桥重要地震响应量的影响程度及其原因,并提出了相应的抗震设计参考建议;丰硕等[16]根据大跨度悬索桥的动力特性和非线性多支承激励地震响应,探讨了行波效应对超大跨悬索桥地震反应的影响;周刘茜[17]研究桩土效应下不同模型对大跨度悬索桥地震动力响应的影响;张新军[18]通过多振型地震反应谱法研究了桥梁结构设计参数对地震反应的影响。
综上所述,本论述对大跨悬索桥的地震响应特性进行统计分析,研究其主要影响因素,并探讨大跨度悬索桥的抗震性能设计。鉴于缺少专门针对悬索桥的抗震设计规范[19],故本论述可对悬索桥抗震分析及合理设计提供有效参考。
1 悬索桥地震响应统计样本
通过分析悬索桥地震响应的文献资料,从中归纳出18座大跨度悬索桥的地震响应分析数据,具体情况见表1所列。
由于本论述样本数据均来自已公开发表的学术资料,故覆盖范围相对较窄;但从大跨度悬索桥地震响应分析而言,本论述采集的数据具有很好的代表性。样本总体主要涵盖单塔、双塔及多塔三类悬索桥;根据跨径大小,可进一步将统计数据分为100~500m、500~1000m、1 000~2 000 m、2000 m以上四类,据统计发现,双塔悬索桥占比高达样本总数的67%,而单塔仅占5%;由此可知,目前大跨径悬索桥主要以双主塔为主。如图1所示:500~1 000 m跨径范围是悬索桥主塔结构应用趋势的拐点;整体而言,单塔结构主要应用在500 m以下的桥跨体系中,当跨度大于500 m时很少采用单塔结构;500~1 000 m跨度范围双塔结构使用率高达100%,而在1 000 m以上的桥跨体系中大多采用多塔结构。
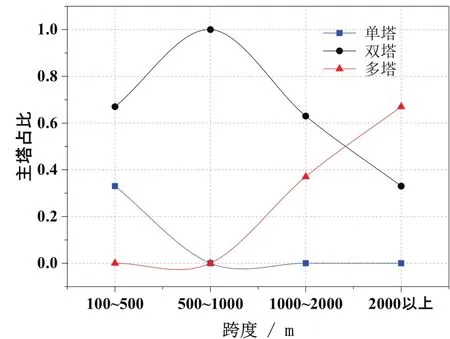
图1 跨度与主塔结构形式关系曲线
样本数据中桥塔绝大部分为钢筋混凝土门式结构,且主缆几乎全部采用高强钢丝。由图2可知,悬索桥主塔高度随着跨度增大而增大,且目前大部分主塔高度在300 m以下。进一步分析主塔高跨比与主缆垂跨比,如图3所示:垂跨比分布区间为0.09~0.18;高跨比分布区间为0.1~0.27,且分布较离散。根据桥梁实际条件,主缆横截面一般随着跨度增大而增大,即大跨悬索桥中主缆自重影响着桥梁跨度;一般而言,桥面以上的桥塔高度取桥跨的1/9~1/11;而主缆垂度为桥跨的1/8~1/12;由此可知,主塔高度、主缆垂度与桥梁跨度三者之间存在着一个相互制约关系,这有待进一步探究。
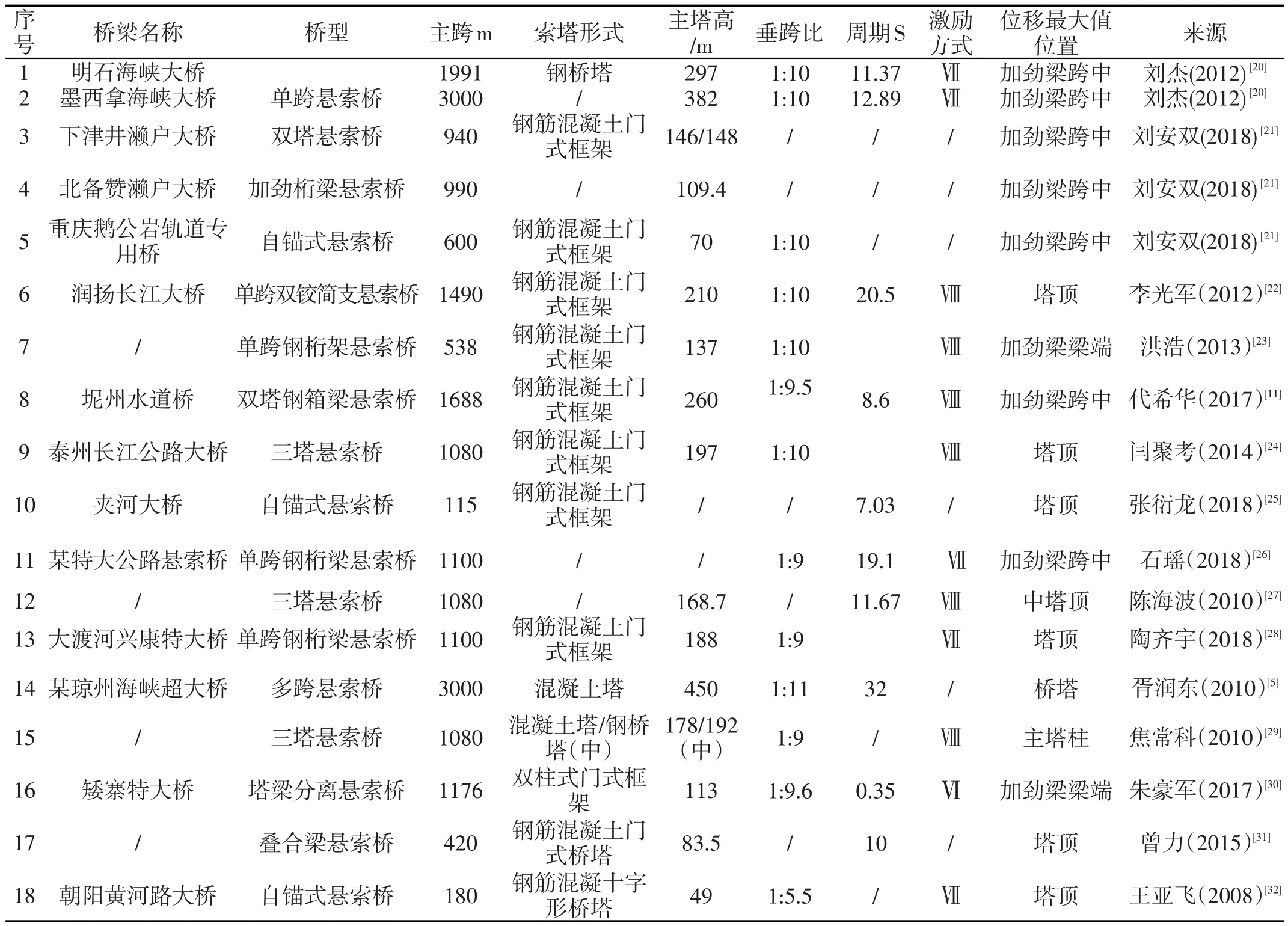
表1 悬索桥结构参数样本数据统计表

图2 跨度与主塔高度分布图
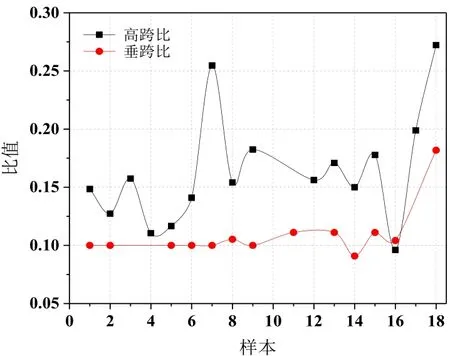
图3 主塔高跨比与主缆垂跨比分布趋势图
2 地震响应影响因素分析
2.1 结构型式
现对悬索桥抗震结构体系的主要特点进行归纳总结,见表2所列。本论述以朝阳黄河路大桥为例,探讨液体粘滞阻尼器的减震效果。见表3所列,液体粘滞阻尼器对位移的具有明显的减震效果,但却会造成塔底内力一定幅度的增加,关于悬索桥主塔分析可采用王翠宏[33]所述的简化方法。因桥梁地震响应及其震害损失与桥梁的结构形式有密切的关系,尤其是大跨度悬索桥的结构形式在地震响应分析中显得尤为重要,所以减震耗能技术也从降低结构地震响应向优化结构性能控制发展。
2.2 多点激励
根据地震空间变化可知,大跨度桥梁在地震作用下,各作用点输入的地震波可能不同,故在地震响应分析中应考虑多点激励,但实际常用顺桥向、横桥向、竖向三种地震荷载组合来进行计算分析;本论述根据样本数据,以主塔位移和弯矩响应进行分析说明。
(1)塔顶位移区间为0.51~25.07 cm,梁端位移区间为8.73~47.11 cm,跨中位移区间为8.65~159.41 cm。由图4可知,大跨悬索桥在地震作用下,塔顶位移相对较小,跨中位移最大;且针对同一座悬索桥而言,跨中位移最大值可达塔顶位移的6倍以上,在竖向荷载作用下,跨中位移与塔顶位移相差不大。
(2)统计显示:激励方向对桥梁结构位移有方向性的影响。如图5所示,竖向激励时塔顶位移最小,而横桥向及横竖组合激励时,塔顶位移突增,最高增幅可达48倍;整体而言,按结构位移响应大小范围可把激励方式分为三类:第一类,横桥向与横+竖向组合;第二类,顺桥向与顺+竖向组合;第三类:竖向。其中,第一类激励时结构位移均值最大,第三类激励时结构位移均值最小,且第一类结构位移均值是第二类结构位移均值的1.3倍左右,是第三类结构位移均值的10倍以上。

表2 大跨度悬索桥主要结构特点一览表
表中:阻尼系数为3 000 kN/(s/m)n;其中n=0.4为速度指数,地震作用激励方式为顺桥向+0.667竖向。
减震率=(无阻尼最大值-安装阻尼最大值)×100%/无阻尼最大值。
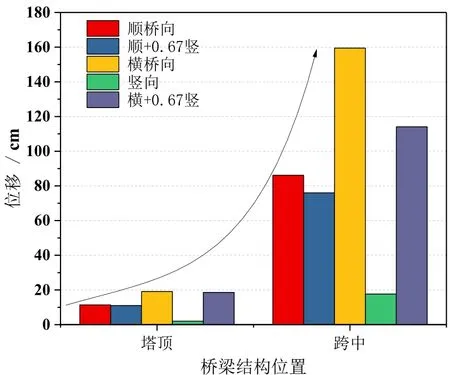
图4 同条件下桥梁地震位移对比图

图5 塔顶位移在不同激励下的统计曲线
(3)如图6所示,弯矩响应在非一致激励下的变化趋势与位移响应相似,但在顺桥向及顺竖组合激励下,塔底弯矩响应最大,其弯矩峰值是横向及横竖组合激励时的2倍左右,是竖向激励时的15倍以上。由此可知,目前主流的桥塔结构(如门式框架桥塔),在地震作用下,受顺桥向弯矩影响较大。

图6 塔底弯矩在不同激励下的统计曲线
2.3 行波效应
地震多点激励空间变化特征主要表现在行波效应、部分相干效应、局部场地效应三方面[28]。而大跨度桥梁地震行波效应往往会起控制性作用[34],尤其是时域内的行波效应在实际应用中占主导位置,故本文主要研究该类行波效应对大跨度悬索桥地震响应的影响,分析发现:
(1)如果不考虑行波效应,因视波速的变化可能会导致在相同结构下的时程分析中得到相反的结果。时域行波效应下不同的地震输入点对地震响应结果影响很大;现有很多文献中,有关锚锭是输入点还是仅为固定边界,时域行波效应下结构关键点的响应时程是相对量还是绝对量等问题没有说明清楚。
(2)行波效应结构动力方程如式(1)所示,其常见的求解方法为直接求解法、大质量法、相对运动法和等效荷载法。在大部分文献中采用ANSYS软件分析时均采用大质量法。
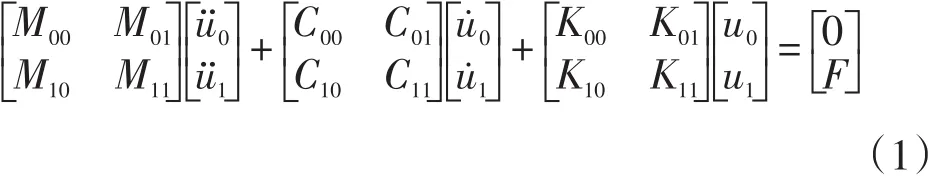
式中:下标1:支承自由度;下标0:非支承自由度;[M]:结构质量矩阵;[C]:结构阻尼矩阵;[K]:结构刚度矩阵;[u¨]:结构加速度;[u˙]:结构速度;[u] :结构位移;F:支承点处荷载

表3 阻尼器减隔震效果
(3)根据统计结果,在不考虑桩土效应,且固定地震波传播方向的情况下,取视波速区间为1 000~4 000 m/s,进行双塔桥梁结构顺桥向地震行波效应分析,为避免误解,本文中地震响应采用相对量。如图7所示:①一致激励下塔柱顺桥向剪力和弯矩大于行波效应的对应值;②由图7(a)可知,塔柱剪力包络线呈K形分布,视波速越大,梁端剪力差异越大。③由图7(b)可知,塔柱弯矩在塔底处随着视波速增大而增大,而在塔顶处视波速影响明显减小,弯矩相差不大。
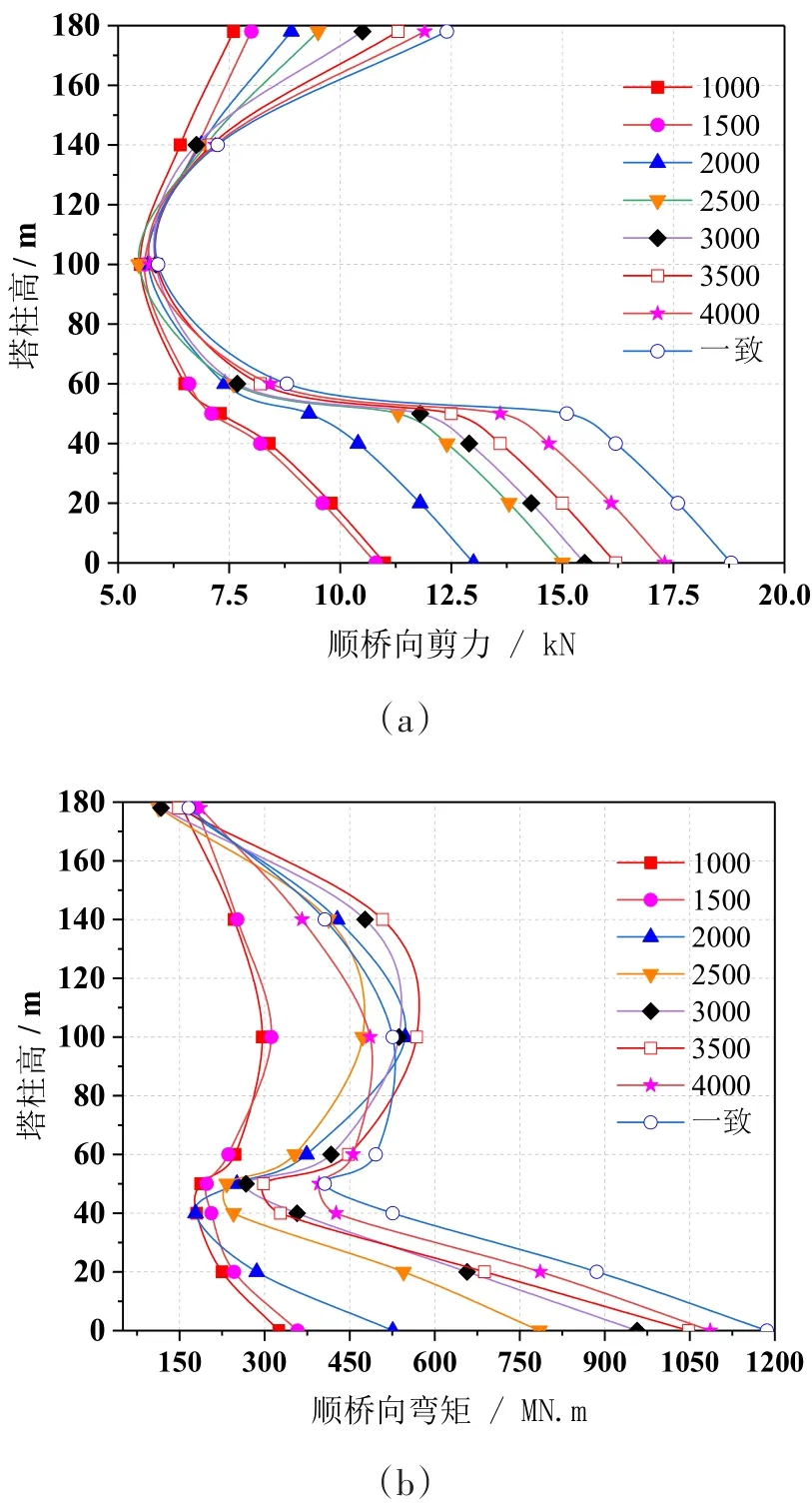
图7 视波速对顺桥向剪力和弯矩的影响
综合而言,当视波速较小时,桥梁相关地震响应随视波速变化振荡较明显,这与地震波选取有很大关系,故不能仅以低视波速来评定行波效应;由于地震方向的不确定性和桥梁场地的特殊性,在大跨度桥梁抗震设计中应取响应较大值作为参考依据,且合理选取地震波尤为重要。
3 结论
(1)桥梁减震耗能技术已从降低结构地震响应向优化结构性能发展。双塔结构是目前大跨度悬索桥的主流结构型式,目前悬索桥大部分主塔高度集中在300 m以下,且主塔高度随着跨度增大而增大,分析表明:主塔高度、主缆垂度与桥梁跨度三者之间存在着一个相互制约关系,这有待进一步探究。
(2)对同一座大跨悬索桥而言,跨中地震位移最大值可达塔顶位移的6倍以上。整体而言,激励方向对桥梁结构位移有方向性的影响,竖向激励下结构位移最小,横桥向与横竖组合激励下结构位移均值可达竖向激励时结构位移均值的10倍以上。顺桥向及顺竖组合激励下弯矩峰值是横向及横竖组合激励时的2倍左右,是竖向激励时的15倍以上。
(3)塔柱剪力包络线呈K形分布,视波速越大,梁端剪力差异越大。塔柱弯矩在塔底处随着视波速增大而增大,而在塔顶处视波速影响明显减小,弯矩相差不大,故不能仅以低视波速来评定行波效应;建议在大跨度桥梁抗震设计中应取响应较大值作为参考依据,且应合理选取地震波。

