基于C#编程实现高斯牛顿法求解激光跟踪干涉仪基站空间坐标
唐文秀,林 虎,薛 梓,秦海濛,铁咪咪
(1.北京信息科技大学 仪器科学与光电工程学院,北京 100192;2.中国计量科学研究院,北京 100029;3.天津大学 精密仪器与光电子工程学院,天津 300072)
1 引 言
随着大型装备制造业的发展,在船舶、轨道交通、航空航天等领域都对大尺寸测量技术及测量设备提出了越来越高的要求。激光跟踪仪是大尺寸测量中常用的测量设备,可用于精密几何测量和三维运动轨迹跟踪,具有测量范围大、速度快、精度高等优点[1]。近些年,各种新型的激光跟踪仪相继被研制出来,其中德国物理技术研究院和英国国家物理实验室共同研制了一种新型激光跟踪干涉仪[2],采用球度误差小于50 nm的标准球作为参考反射镜,该标准球固定在热膨胀系数极小的殷钢支柱上,干涉测量系统仅围绕该固定标准球转动,因此机械结构对于精度的影响可以降低到很小,并且只利用干涉测量长度进行空间坐标的解算,避免了角度测量引入的误差,具有很高的精度[3,4]。其中基于多边法的四路激光跟踪三维坐标测量技术是近年的研究热点[5~9]。四路激光跟踪三维坐标测量系统在实际应用前首先需要进行系统多参量自标定,确定出跟踪干涉仪的基站坐标。系统多参量的自标定过程本质是一个非线性最优化问题,求解非线性最优化问题常用的方法有高斯牛顿法、Levenberg-Marquart法、信赖域法等等[10]。高斯牛顿法由于避免了计算大规模的Hessian矩阵所带来的不便,极大地简化了运算量,实际应用广泛。因此,本文通过C#与MATLAB混合编程、C#语言编程两种方式实现高斯牛顿法求解激光跟踪干涉仪基站空间坐标值。
2 激光跟踪干涉仪基站空间坐标标定原理
如图1所示为激光跟踪干涉仪基站空间坐标标定原理图,对于多台激光跟踪干涉仪组成三维坐标测量系统,其每个基站坐标标定原理类似。在全局坐标系统中,激光跟踪干涉仪第j个基站坐标为(x0j,y0j,z0j)(j=1,…,4),对于任意空间目标点Pi(xi,yi,zi),激光跟踪干涉仪可以测出其相对初始目标点P0(x0,y0,z0)的相对长度变化量Δlij=lij-l0j,这里需要求解基站坐标及到初始目标点的长度值l0j。为了对上述参量进行标定和求解,需要在全局坐标系统中设置一系列已知的目标点Pi(xi,yi,zi)(i=1,2,…,m),利用激光跟踪干涉仪对上述目标点进行依次测量,根据基站坐标、初始点坐标及目标点坐标的空间几何关系可以建立如下方程组:
(1)
在上述方程组中,需要求解的未知参量为(x0j,y0j,z0j,l0j),为了获取更高的解算精度,需要更多的冗余方程,即目标点的数量要大于4个,此时方程个数大于待求参量个数,构成超定方程组。超定方程组没有通常意义下的确定解,但是可通过数值算法解算出近似最优解。因此,求解激光跟踪干涉仪基站空间坐标问题转化为对非线性超定方程组的最优化求解,如何进行最优化求解并且通过C#编程实现成为本文研究的关键内容。

图1 激光跟踪干涉仪基站空间坐标标定原理图
3 高斯牛顿算法求解原理
(2)
进一步可推导为:
(3)
上述非线性超定方程组具有一定的平方和结构特殊性,属于小残量问题,因此,可选用高斯牛顿法求解非线性超定方程组的最优解。该算法对于非线性拟合具有较好的拟合精度,收敛速度较快,对初值依赖强,必须合理选取初值,它通过舍弃Hessian矩阵的二阶偏导数实现,可用于数据拟合、参数估计和函数估计等方面,并且在实际应用中,常用于目标定位、单点定位等坐标求解问题[11~13]。

ri=(b4+Δlij)-
(4)
求解该最小二乘问题即让目标函数最小,数学表达式为:

m>4
(5)
将f(b)按泰勒公式在bk处展开并略去高阶项:
f(b)=f(bk)+g(bk)T(b-bk)+
(6)
函数ri(b)二次连续可微,目标函数的梯度g(b)与Hessian矩阵G(b)分别为:
(7)
=J(b)TJ(b)+s(b)
(8)
根据高斯牛顿迭代法,对ri分别求b1、b2、b3、b4的偏导,其中初值为b0=[b01,b02,b03,b04],[b01,b02,b03]为根据空间位置粗略估计激光跟踪干涉仪初始坐标,b04为激光跟踪干涉仪到初始动点的迭代初始值,构成的雅克比矩阵J如下所示:
(9)
将g(b)与G(b)代入式(6)可得:


(10)
忽略Hessian矩阵的二阶偏导s(bk)后,根据牛顿法推导可得高斯牛顿迭代公式为:
bk+1=bk-(JTJ)-1JTr(bk)
(11)
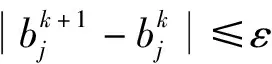
4 C#与MATLAB混合编程关键技术
为了实现最优解的快速迭代求解,可直接在科学计算软件MATLAB中调用相关函数。MATLAB具有丰富的函数库,专门用于数值分析,调试简单,但不擅长于后续测控软件开发。为了求解出激光跟踪干涉仪基站空间坐标,并且显示到用户界面中,方便用户进行数据分析处理,本文考虑采用C#与MATLAB混合编程,由C#实现用户界面设计,MATLAB实现最优解的快速迭代求解,C#与MATLAB采用.NET组件技术实现混合编程,在MATLAB中调用lsqnonlin函数并编译生成动态链接库(Dynamic Link Library,DLL)文件,在C#中添加该.DLL文件引用,即可在C#中执行与MATLAB同样的计算功能[14~18]。具体实现步骤如下:
(1)在MATLAB中新建一个.m文件,运行编译工具(deploytool),生成动态链接库。
(2)打开C#,添加该引用以及程序集文件“MWArray.dll”并加入命名空间,MWArray是用于C#与MATLAB之间的数据交换类。
(3)在C#中进行数据类型转换,调用动态链接库开始计算,并将结果返回到界面中显示。
C#与MATLAB混合编程的方式可充分发挥两种语言与平台的优势,特别是调用MATLAB的数学函数能保证迭代算法的正确性,但是混合编程的方式也存在其缺点:一是运行程序之前必须提前安装整个MATLAB软件,准备工作比较繁琐,而最终只用到其中的几个函数,当程序需要商业化时,其经济性就凸显不足;二是每次运算时,数据需要频繁地在两个平台之间传输,当测量点数量较多时,程序的运行速度大大减慢,也不利于软件界面的开发。为解决上述不足,本文进一步研究了仅依靠C#语言编程来实现高斯牛顿法求解激光跟踪干涉仪基站空间坐标,并通过与MATLAB混合编程的结果比较,验证C#编程算法的准确性。
5 C#实现高斯牛顿算法
5.1 数据定义
定义已知的m个目标点的空间坐标,l为激光跟踪干涉仪的测距读数,b为待求参量(x0j,y0j,z0j,l0j)T,设置迭代次数为20次,精度因子为10-8。
5.2 设计类进行矩阵运算
设计一个类为Matrix用于矩阵的运算,包含矩阵的加法、减法、乘法、转置以及求逆,并且在计算之前进行是否符合矩阵运算的规则判断。
5.3 重复迭代计算
根据激光跟踪干涉仪在三维空间的位置估计,给出一个粗略的迭代初值,开始迭代循环计算,并最终得到满足精度因子的解。
第1步:按式(4)定义残差公式数学模型;
第2步:求出雅克比矩阵J及其转置矩阵JT,其中ri对b1、b2、b3、b4的偏导分别为:
(12)
第3步:求出的矩阵JTJ,以及残差ri;
第4步:计算(JTJ)-1JTri,代入迭代公式bk+1=bk-(JTJ)-1JTr(bk);
6 实验验证
如图2所示,利用三坐标测量机及激光跟踪干涉仪搭建实验系统,激光目标靶镜装在三坐标测量机的测头座上。在该实验系统中,三坐标测量机的机器坐标系为全局空间坐标系,激光跟踪干涉仪的基站空间坐标是未知的,三坐标测量机的坐标读数为激光目标靶镜的坐标值,当激光目标靶镜在全局空间坐标系内运动时,激光跟踪干涉仪能够跟踪目标靶镜并进行长度测量。

图2 激光跟踪干涉仪基站空间坐标标定实验
利用上述实验系统对激光跟踪干涉仪开展基站空间坐标标定实验。首先将激光跟踪干涉仪置于第1个站位LT1上,令激光目标靶镜在全局坐标系中运动至设定好的6个目标点,测量每个目标点相对初始目标点的相对长度变化值;然后将激光跟踪干涉仪陆续移动至第2个站位LT2和第3个站位LT3,在每个站位下令激光目标靶镜运动至不同的6个目标点,分别采集激光跟踪干涉仪的数据如表1所示。

表1 空间目标点坐标及激光跟踪干涉仪测距读数
将表1中数据分别导入到C#的两个程序代码中,第一个程序代码为C#与MATLAB混合编程,第二个为C#编程,编程软件平台为微软Visual Studio 2017。
在两个程序中分别对激光跟踪干涉仪的基站空间坐标进行优化迭代计算和求解,迭代初值为每个基站站位的估计值,基站站位的精确计算结果以及两种方式的运行时间如表2所示。

表2 C#编程与C#调用MATLAB计算结果
从表2列出的激光跟踪干涉仪3个基站空间坐标计算结果可以看到:采用C#编程的高斯牛顿法在迭代5或6次后即与C#调用MATLAB的计算结果一致,差值在10-7数量级;并且从运行时间来看,用时更少,效率更高。实验结果表明C#编程实现了高斯牛顿算法对非线性超定方程组最优解的快速求解,验证了利用C#编程求解激光跟踪干涉仪基站空间坐标的准确性以及可行性。
7 结 论
本文将激光跟踪干涉仪空间坐标标定问题转化为非线性最小二乘问题,采用C#编程实现了高斯牛顿算法。通过实验将C#编程计算结果与C#调用MATLAB的计算结果相比,差值在10-7数量级,并且效率更高,验证了C#编程算法的正确性以及可行性,说明了高斯牛顿法进行非线性拟合具有较好的拟合精度,收敛速度较快,为后续进行多个站位下的联合测量以及利用多边法原理反求动点运动轨迹研究打下了基础。

