基于门控循环神经网络的线损电量预测方法

国网甘肃省电力公司 李云冰 徐兰兰 王晓军 张小玲

1 引言

电网线损电量预测是提高供电企业管理水平、优化电网经济运行、实现节能降损的一项基础工作，文献[1]利用牛顿拉夫逊法，采用负荷电量来计算低压配电台区理论线损电量；文献[2]通过合理地获取负荷和基于该负荷的潮流计算方法实现了对配电网理论线损的计算；文献[3]提出一种基于前推回代法的配电网损耗计算方法。然而，上述基于潮流计算的传统配电网损耗计算方法多数是依赖于配电网的网络结构，因而无法挖掘大量数据与配电网损耗之间的关系。事实上，随着智能电网的建设，电力监测系统中已经积累到了大量的数据，这为配电网损耗计算和评估提供了条件与新途径。文献[4]提出了一种基于改进K-Means聚类和BP神经网络的损耗计算方法，该方法无需建立精准的数学计算模型，通过利用神经网络自身强大的自学能力以及非线性处理能力，可以实现损耗及其影响特征参数之间的关系。文献[5]提出一种基于随机森林的损耗计算方法。但是，基于BP神经网络、向量机浅层学习模型的配电网理论电网损耗计算方法多数仅具有单层的逻辑结构，需要手工指定特征且易出现局部最优问题，因而在数据特征提取表达能力、数据间非线性关系建立方面均存在缺陷。

深度学习的基本思想是构建包含多层隐含层的网络结构，可自动逐层从样本数据中提取深层特征，更加完整地表征数据内部的丰富信息，进而实现对数据关系的分析。本文在介绍门控循环神经网络的深度学习理论基础上，进一步搭建了基于门控循环神经网络的配电网损耗计算模型，并对模型进行了训练，探寻历史数据中输入数据与输出数据之间的隐含关系，最后通过算例分析，研究算法性能及配电网损耗计算精度。

2 循环神经网络基本原理及其局限性

循环神经网络（Recurrent Neural Network，RNN）作为深度学习模型的典型代表之一，是一类用于对序列数据建模的神经网络。RNN的信息在层内、层与层之间可双向传递，网络中当前神经元的输出与之前的输出也相关，网络会对前面的信息进行记忆并应用于当前神经元的计算中，即隐含层之间的节点也是有连接的，并且隐含层的输入不仅包括输入层的输出，还包括上一时刻隐含层的输出，因而可充分利用数据中时序信息的深度表达能力，为处理序列数据带来了强大支撑，并在语音识别、机器翻译及时序分析等方面实现了突破。

图1展示了一个典型RNN结构及其网络展开示意图。由图可知，RNN对长度为N的序列展开之后，可视为一个有N个中间层的前馈神经网络。因此RNN网络中，对于一个序列数据，当前神经元的输出与之前的输出是相关的，网络会对之前的信息进行记忆并应用于当前神经元的计算，即隐含层之间的节点是有连接的，并且隐含层的输入不仅包括输入层的输出还包括了上一时刻隐含层的输出，故RNN可更好地利用传统神经网络所不能建模的信息。理论上RNN可处理任意长度的序列数据，但由于t时刻需要考虑t时刻之前所有时间步骤所带来的输入，因此随着输入数据时间增加，将引起梯度在传递的过程中随时间产生累计，出现梯度消失和梯度爆炸问题，即RNN在实际使用过程中会面临长期依赖问题。

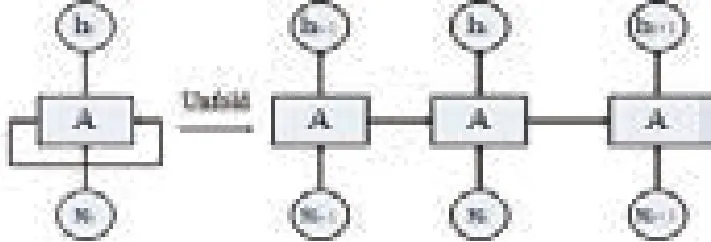
图1 典型RNN结构及其网络展开示意图

3 门控循环神经网络基本原理

K.Cho等于2014年提出门控循环神经网络（Gated Recurrent Unit，GRU）。GRU属 于RNN的一种改进，可以更加简单的结构带来更加高效的训练，进一步减少梯度弥散和梯度消失问题（图2）。

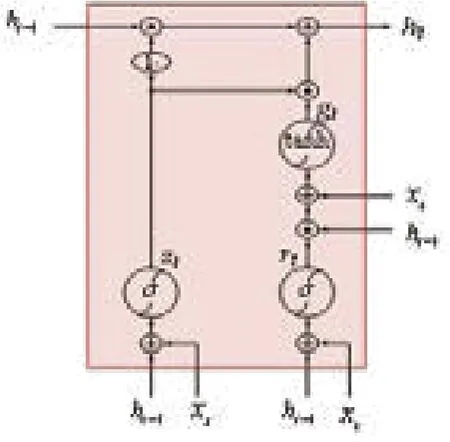
图2 GRU结构图

GRU单元取消了输出门，单元的全部状态就是该时刻的单元输出。与此同时，GRU单元还增加了一个控制门来控制哪部分前一时间步的状态在该时刻的单元内呈现。在t时刻GRU的计算表达式如式（1）所示，其中，Wxr，Whr为重置门的权重矩阵；Wxz，Whz为更新门的权重矩阵；Wxg，Whg为形成当前记忆时的网络权重矩阵；br，bz，bg为偏置矩阵。

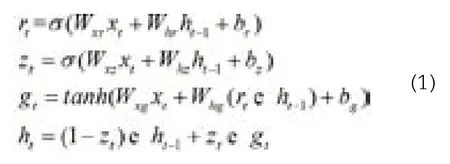
4 基于GRU的线损电量预测方法

4.1 基于GRU的线损电量预测模型

系统线损电量具有非线性、随机性和时序性的特点，可通过数据驱动方法来进行线损电量的预测。针对本文提出的基于GRU进行线损电量预测方法的总体流程图如图3所示，具体过程如下：

确定模型的输入量及输出量，并对输入数据和输出数据进行预处理。在本文方法中，输入数据是指影响线损电量的各种因素，包括有功供电量、无功供电量、专变月有功供电量、专变月无功供电量、公变月有功供电量、公变月无功供电量、公用变压器台数及总容量、公用变压器平均负载率、功率因数、三相不平衡度、温度、湿度、是否节假日；输出数据则为对应时刻的实际线损电量数据。结合历史数据，输入数据与输出数据便可构成样本数据集。在此基础上，分别采用min-max标准化、one-hot或log（x+1）/log（max+1）的方式进行数据预处理，并将预处理后的数据集按照60%、20%、20%的方式依次划分为训练数据集、测试集和验证集。

建立基于GRU的线损电量预测模型，并利用训练集对模型进行训练，利用验证集最终确定模型GRU层数、学习率等模型参数。本文所提出的用于线损电量预测的GRU模型如图4所示，该模型包含了1个输入层、多个由GRU单元构成的隐含层、1个输出层。隐含层为模型的核心部分，主要是用来建立输入信息与输出线损电量之间的非线性关系。通过采用“预训练+参数微调”方式利用训练数据集。具体地，利用多GRU层的堆叠实现逐层数据特征提取，通过组合底层特征形成更加抽象的高层特征，最终揭示输入数据与输出数据之间的内在隐含关系。

利用测试集估计模型的泛化误差，并确定模型性能是否满足准确率的要求。若不能满足预测准确率要求，则需要重新确定模型的隐含层数、学习率等模型参数，直至满足误差要求为止。

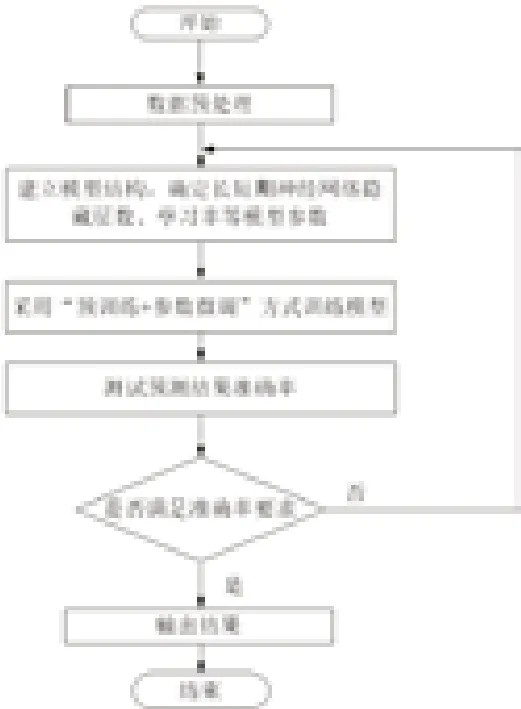
图3 基于GRU的线损电量预测流程图

4.2 算例分析

本文采用TensorFlow的深度学习框架，编译环境为Python3.6.8；处理器为i7-8086K，GPU为GTX 1080 Ti。

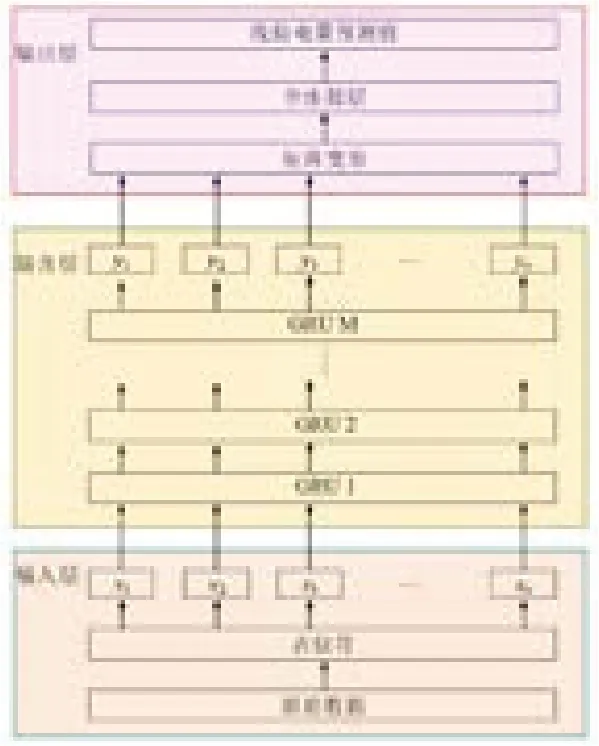
图4 基于GRU的模型整体结构

4.2.1 模型参数设置

在建立网络模型时必须要面对这样一个问题：算法中的不同超参数控制不同方面的算法性能。有些超参数会影响算法运行时间和存储成本，有些超参数会影响学习到的模型质量以及在新输入上推断正确结果的能力。对于某些超参数，当参数值太大时会发生过拟合，譬如中间层隐藏单元的数量，增加数量能提高模型的容量容易发生过拟合。而对于某些超参数，当参数的数值太小时也会发生过拟合。譬如，最小的权重衰减系数允许为零，此时学习算法具有较大的有效容量，反而容易过拟合。

学习率是最重要的超参数，当学习率过大时梯度下降可能会增加而非减少训练误差；当学习率太小，训练不仅慢，还可能永久停留在一个高的训练误差上。调整学习率外的其他超参数时还需要同时监测训练误差和测试误差，以判断模型是否过拟合或欠拟合，然后调整其容量。因此，需要综合考虑各超参数与线损电量预测准确率之间的关系及其作用规律，在此基础上获得各超参数。当前的机器学习中，上述各超参数的选择往往是通过尝试的方式。本文通过反复试验，最终确定的模型参数为：隐含层数4，GRU每层神经元数目512，迭代次数200，世代数目1000，训练批次200，学习率0.00015。

4.2.2 结果分析

损失函数是用于衡量模型预测得到的线损电量与真实线损电量的差异程度，若预测结果与实际线损电量差距越大，则损失值Loss越大；反之，若预测结果与实际线损电量差距越小，则损失值Loss越小。本文选用交叉熵作为损失函数，用以计算模型预测得到的线损电量与真实线损电量的差异程度。交叉熵的基本原理为。

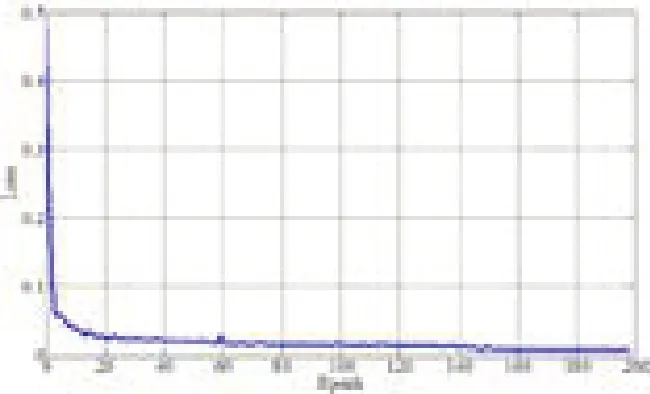
图5 损失值Loss与训练Epoch之间的关系

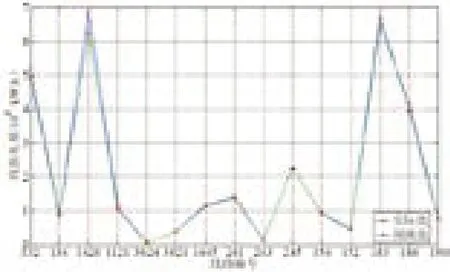
图6 线损电量预测值与实际值对比图

本文利用Tensorflow人工智能框架，Python语言编写，Jupyter Notebook编程环境。损失函数值Loss随着迭代Epoch变化关系如图5所示。由图可知，损失函数随迭代Epoch增加而逐渐降低，这也说明模型的训练结果越来越好，准确率也越来越高。在训练结束后，利用测试样本集对线损电量进行预测，得到的预测结果与实际结果对比如图6。验证表明，本方法具有较好的收敛性和泛化能力，以及较高的预测准确率。