基于分组一致性协议的多微网分层优化调度方法研究

国网甘肃省电力公司电力科学研究院 赵龙 张珍珍 丁坤 周强

北方工业大学电气与控制工程学院 万庆祝 李俊涛

微网优化调度的方法主要有集中式控制和分布式控制，文献[1]研究了基于一阶离散一致性协议的分布式经济调度算法，无需中央处理器，即可实现系统的运行成本最小化；文献[2]分析了储能单元、柔性负荷参与下的分布式经济调度控制效果；文献[3]引入了分布式静态参数估计方法，加快了基于一致性协议的经济调度计算速度；文献[4-5]分别讨论了结合下垂控制与经济调度的直流、交流微电网分布式控制策略。上述文献所研究算法在微网内任一单元控制量波动时，需要所有智能体参与调节，由于可再生能源发电方式具有随机性、间歇性，智能体将随功率的波动而频繁调节，对系统稳定运行造成隐患。

本文提出一种适用于多微网的分布式优化调度算法。该方法无需中央处理器，仅需有限个邻居节点间的信息交互。通过分组一致性迭代，既保证了各子微网运行于符合各自需求的控制目标，消除了全局跟随调节效应，又实现了降低多微网系统运行成本的目的。

1 多微网运行调度模型

针对多微网经济调度模型，首先计算各子微网的经济成本，对所有子微网的经济成本求和，线路损耗可忽略不计，无功功率发电成本不在本文考虑范围内。

1.1 目标函数

多微网的优化调度需保障系统运行稳定条件下，并使系统总成本在运行周期内最小，即CMGx=min(ΣCx(PG,t)+ΣCx(PL,p)+ΣCx(PB,q))，式中Ctotal、CMGx分别为多微网系统、子微网x的最小运行成本；Cx(PG,t)、Cx(PL,p)和Cx(PL,q)分别为子微网x中第t个可控微源、第p个可控负荷和第q个储能单元的运行成本。

1.2 成本算式与约束条件

1.2.1 各单元成本

1.2.2 约束条件

等式约束主要考虑区域切分或由多个子微网组成的多微网系统，其内部各子系统的功率平衡。不等式约束主要以各运行单元的输出或吸收功率上下限为界限。等式约束条件：式中PRG,c为子微网x中第c个可再生能源发电单元输出有功功率。

不等式约束条件：

2 基于分组一致性协议的多微网优化调度

2.1 单微网分布式经济调度算法

基于多智能体系统的分布式经济调度算法一般以微增率成本为控制量，结合一阶离散一致性协议，给出计算方程：

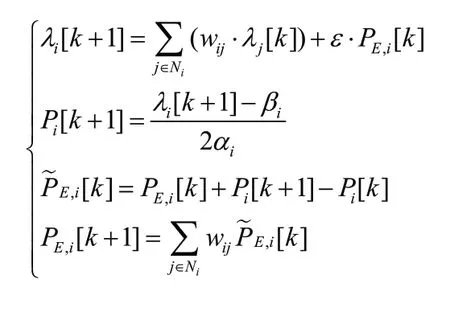
式中λi[k]为可控单元i在第k次迭代时的微增率成本；ε为收敛系数，通过改变收敛系数的取值可以改变系统的收敛效果；PE、i[k]为本地功率误差估计的第k次迭代值。

2.2 多微网分布式优化调度算法

单微网分布式经济调度算法无需中央处理器，大大减小系统计算负担，但系统内部任何一个单元的功率需求变化都要求所有可控单元参与调节，以达到新的平衡状态。本文所提分组一致性算法各子系统分别实现各子系统的控制目标，而不影响其他子系统的平衡状态，有利于解决单微网全局跟随调节问题，因此本文引入分组一致性协议进行多微网优化调度。以微增率成本为控制变量，有式（1）：

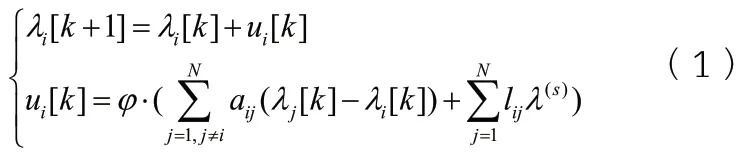
式中λ(s)为子系统s的一致性平均值。

为获取各子微网的微增率成本一致性平均值，需要设置一个可获取所有单元控制量初值的中央处理器，这与分布式控制的思想存在矛盾。为此本文采用两阶段计算方式，首先通过单微网分布式调度算法求解各子微网的一致性平均值；其次考虑各子微网间智能体的交互影响，基于分组一致性协议进行各可控单元的微增率成本运算（图1）。

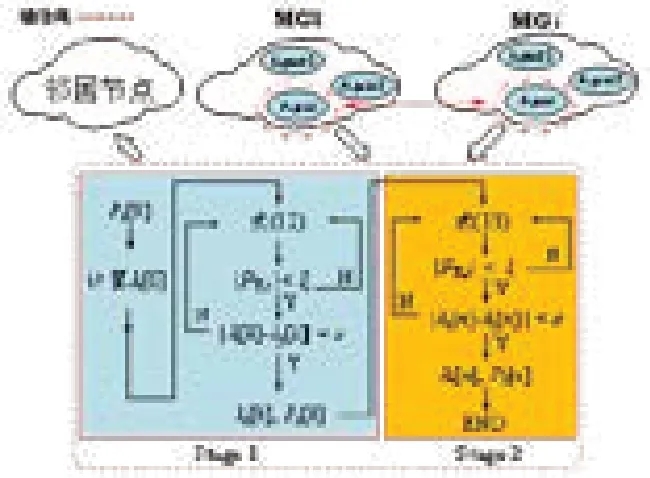
图1 基于分组一致性协议的多微网分布式优化调度算法

3 仿真分析

3.1 系统结构与参数

本文基于IEEE14节点电气拓扑结构，构建智能微电网，其中通信拓扑的连接线路与电气拓扑的连接线路相同（图2）。

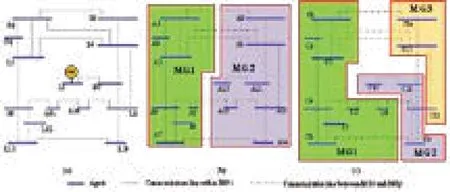
图2 微电网通信拓扑结构

图2(a)所示为基于IEEE14节点结构所搭建的单微网通信拓扑。负荷L8所在的母线处，接入了采用最大功率输出的可再生能源发电单元。图2(b)和(c)分别为以IEEE14节点为基础框架的含两个微电网和含三个微电网的多微网系统。本文假定图2所示的系统隶属于同一个利益集体，即多微网的控制目标为在保障各子微网内部供需平衡的前提下实现多微网系统的运行成本最小化。图2(b)、(c)中，为便于区分，分别采用A和C表示其内部单元。图2所示的单微网及多微网，系统参数如表1所示。系统参数确定后，基于微增率准则的经济调度算法，在外界功率需求为零时，可控单元的最优微增率存在且唯一；当外界功率发生波动时，各可控单元微增率将收敛至新的一致性平均值。

3.2 单微网运行

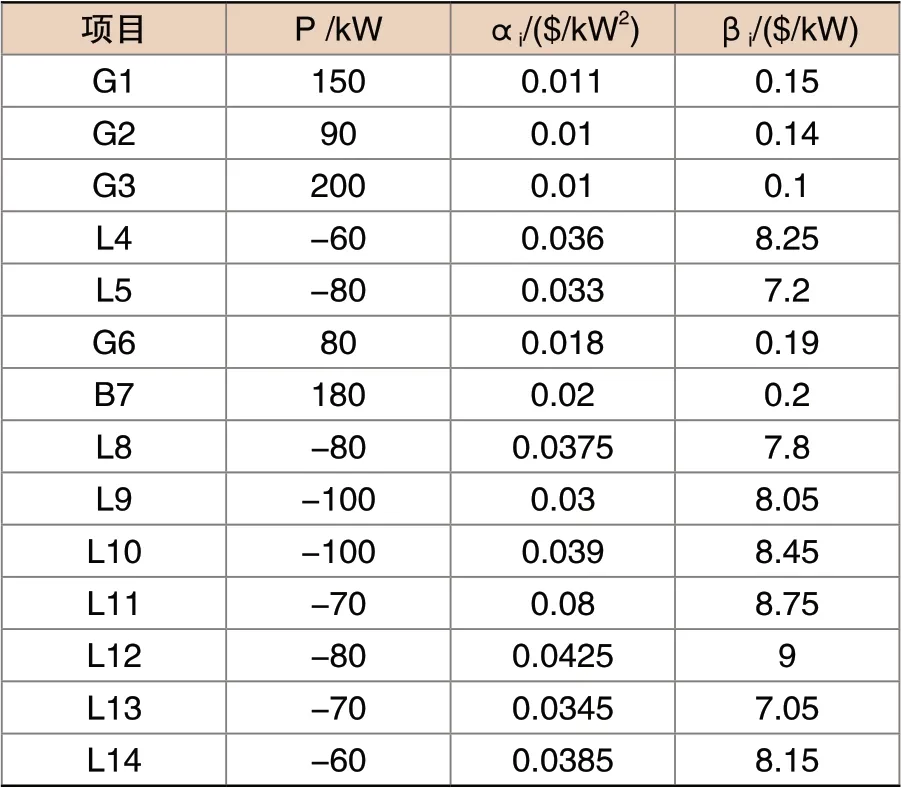
表1 系统参数

以新能源发电单元为功率需求来源，仿真从微增率成本求解精度和迭代次数两个角度，分析收敛系数的取值对系统收敛效果的作用。

图3 收敛系数对收敛效果的影响

由图3可知，功率需求为零时系统的一致性平均值为3.0668。收敛系数在[-10×10-3,0]区间上，收敛系数的增大，使得迭代次数先减小后增大，并且收敛系数取-8×10-3时迭代次数最少。当收敛系数取值在[-10×10-3,-6×10-3]上时微增率收敛值偏离3.0668较远，而在[-6×10-3,0]区间上计算误差小于0.001。综合考虑收敛速度与计算误差，本文取收敛系数ε=-2×10-3。考虑新能源发电单元出力为零和出力增加至50kW两种情况，单微网分布式经济调度算法仿真结果如图4。

图4(a)中，新能源发电单元出力为零时，微网内所有可控单元参与调节，最终实现一致性收敛。由图4(c)和(d)可知，系统达到一致性时，本地功率误差和系统功率不平衡度均降至0kW。当新能源出力增加至50kW，原有功率平衡被打破，各可控单元在一致性协议的作用下重新进行调节，并达到新的收敛值2.9084，此时各单元的本地功率误差仍为0kW。

3.3 多微网运行

针对图2（b）进行仿真如图5。可知功率需求为零时，MG1和MG2实现一致性，收敛值分别为2.2877和3.9872，实现了多微网系统的经济调度。

图4 考虑新能源功率波动的单微网一致性计算结果

图5 MG1与MG2内部各单元的微增率成本

3.4 运行成本分析

图6 多微网运行成本

单微网和多微网系统在功率需求为零时的运行成本结果如图6，可知多微网运行成本为10904.24$，单微网运行成本为27528.42$，多微网运行低于单微网运行成本，随着微网数量的增加多微网运行成本进一步下降，但成本下降幅度不高。