基于非线性规划和有限元法的悬臂式桁架优化设计

马佳 吴世宝 张瑞媛 高婧

摘要：为了对悬臂式桁架结构进行改进与优化，提出了一种更为简单可行的非线性规划模型。首先，在充分分析悬臂式桁架使用要求的基础上，創新性地将悬臂端节点挠度和结构的可靠性分别视为目标函数和限制条件，并通过静力学分析确定了目标函数和限制条件的具体表达式。然后，利用Python语言编程对优化方案进行求解，发现在给定的限制条件下，当桁架的总长为4 m、总高为26 m且杆件的横截面积为1 400 mm2时，悬臂端节点的挠度最小。最后，利用ABAQUS软件并根据有限元法来判断优化方案的合理性。有限元法的计算结果表明：得出的优化方案是较为准确合理的，且适当减少桁架的总长并增大桁架的总高和杆件的横截面积，可以降低悬臂端节点的挠度。因此，基于非线性规划模型提出的目标函数和限制条件为其他类型桁架结构的优化设计提供了新思路。

关键词：非线性规划;有限元法;悬臂式桁架; Python;ABAQUS

中图分类号：O342文献标识码：A

doi： 10.7535/hbgykj.2020yx03011

Abstract：

In order to improve and optimize the structure of the cantilever truss， a more simple and feasible nonlinear programming model was proposed. First of all， based on fully analyzing the requirements of cantilever truss， the deflection of the cantilever truss end node and the reliability of the structure were innovatively regarded as the objective function and the constraint condition respectively， and the static analysis was carried out to figure out the specific expressions of the objective function and the constraint condition. Subsequently， the optimization scheme was solved by Python language programming， which revealed that with the total length of this truss of 4 m， the total height of

2.6 m and the crosssectional area of 1 400 mm2， the deflection of the cantilever truss end node was minimum under the given constraints. Finally， ABAQUS software was utilized to judge the rationality of the optimization scheme based on finite element method. The calculation results of finite element method demonstrate that the optimization scheme is correct and reasonable to some extent. In addition， decreasing the total length of truss and increasing the total height of truss and the crosssectional area of the bars appropriately can reduce the deflection of this cantilever truss end node. Therefore， the objective function and the constraint condition of the nonlinear programming model can provide a new idea for presenting better optimization design model of other types of truss structures.

Keywords：

nonlinear programming; finite element method; cantilever truss; Python; ABAQUS

作为一种格构化的梁式结构[1]，桁架结构以其优越的承载能力以及抗拉（压）性能，被广泛应用于建筑、煤矿、机械、航空、船舶等诸多工业领域的大跨度主承力结构中。因而，研究这类大跨度桁架结构的力学特性、结构强度、仿真分析和施工技术对充分发挥此类结构的承载能力和保障结构安全具有十分重要的意义。例如，张国伟等[2]利用静力试验和ABAQUS软件对影响M型钢桁架组合楼板的保温与受力性能的参数进行了研究，发现增加型钢厚度和钢筋直径可以有效地提高楼板的承载能力;袁国平等[3]对大型煤场中广泛使用的大跨度拱形拉索桁架结构的关键施工技术进行了总结，指出在施工时应主要对跨中节点进行监测，且应适当增加拉索的实际内力;廖能解等[4]基于SolidWorksWorkbench平台对某种桁架机器人的2种典型工况进行了静力学分析和模态分析，指出当伺服电机的激振频率在40～50 Hz时，不会影响桁架机器人的工作精度以及稳定性;李元章等[5]根据积木式验证方法对某飞艇的桁架式复合材料龙骨结构进行了强度验证，认为根据此方法得出的强度结论满足工程应用需要，且结论偏向保守;崔宏林等[6]采用直接计算法对某艘钢管桁架式连接桥结构的小型双体船的连接桥部位进行了局部强度评估，认为在5级海况下，横向支撑杆件和强、弱框架都无法满足规定的强度要求。

正如文献[6]所指出的，一旦桁架结构不再满足规定的使用要求，则必须对其进行改进与优化，以重新达到目标要求。因而，研究桁架结构的优化模型或优化算法对获得更为合适的优化结果有着重要的指导价值。例如，乔心州等[7]基于区间变量描述不确定参数提出了一种具有非概率可靠性的桁架结构形状优化模型，并发现此模型可以快速稳定地得到收敛的最优解，且符合工程设计经验;郝宝新等[8]改进了传统的桁架结构拓扑优化模型，并提出了一种综合考虑多种约束的桁架结构拓扑优化模型——半定规划模型，此模型有效地解决了在应用传统拓扑优化模型时出现的优化模型非凸以及多重特征值不存在常规梯度等问题;李彦苍等[9]通过在传统的海豚群算法中引入信息熵的方法来减少盲目搜索，并发现改进后的海豚群算法在克服了传统海豚群算法容易陷入局部最优解问题的同时，表现出更好的收敛速度和寻优精度;李沛豪等[10]通过在粒子群算法中设置更为合理的罚函数机制来对桁架结构截面进行优化设计，并指出与传统的粒子群算法相比，改进后的粒子群算法稳定性更好，寻优效率更高。

基于上述分析，为了确定某个悬臂式桁架的优化方案，以悬臂端节点挠度最小为目标函数，利用一个非线性规划数学模型，在控制杆件的尺寸并保证杆件不发生破坏的前提下，结合Python语言编程，求得悬臂端节点的挠度最小时桁架结构中杆件的尺寸。随后，利用Python计算出的优化尺寸，在ABAQUS软件中建立此桁架的力学模型并根据有限元法计算出悬臂端节点的挠度、铰支座支反力和杆件应力，通过对比Python计算出的最小挠度和ABAQUS软件计算出的最小挠度以及观察ABAQUS软件计算出的铰支座支反力和杆件应力是否满足相应的约束条件，来判断优化模型是否合理。

1优化模型的建立

在对悬臂式桁架结构进行优化设计时，一般需要结合实际情况考虑以下几个方面的问题：1）由于工作空间有限，需要对桁架结构中各个杆件的尺寸（如长度、横截面积等）进行必要的限制;2）由于悬臂式结构一般都是用铰支座固连到墙壁上，因而在桁架承受一定的外载荷后，铰支座处会产生相应的约束力，其大小不能超过规定的许用值;3）由于桁架结构中的杆件在受到外载荷后都会产生拉伸或压缩变形，其拉应力或压应力不能超过材料的许用拉应力或压应力;4）对于悬臂式结构，其最大的变形往往发生在悬臂端，因而在优化悬臂式桁架时，也要求其悬臂端节点的挠度尽可能小。由此可见，这一优化模型的目标函数和限制条件不都是线性函数，其中也包含许多非线性函数。因而，可以基于非线性规划的原理[11]来建立悬臂式桁架结构的优化模型。

1.1构建目标函数

由上述分析可知，悬臂端节点的挠度最小，可以作为此优化模型的目標函数。在已知悬臂式桁架结构所受的外载荷时，可以使用单位载荷法（莫尔积分）来计算悬臂端节点的挠度[12]。设此桁架结构中共有

n个长度不完全相等的杆件，它们的弹性模量均为E，横截面都是面积为A的圆，由单位载荷法可得悬臂端节点的挠度y的表达式为

1.2.2限制铰支座所受的约束力

为了保证结构的安全，需要将铰支座所受的约束力限制在一定的范围内。设此桁架结构与墙壁之间共有m个铰支座，且各个铰支座所受的总约束力为Fj，其大小可以通过静力学分析求出。若其许用值为[F]，则此约束条件可表示为

2算例分析

2.1工程概况

某悬臂式桁架简化后的桁架结构及其受到的外载荷如图1所示。此结构中的杆件均由Q235钢制成，其弹性模量为211 GPa，屈服极限为235 MPa，A为横截面积;A—J为铰接的节点;K和L是铰支座，其中铰支座K是固定铰支座，铰支座L是可动铰支座，且水平方向2个相邻节点之间的距离均为a，竖直方向2个相邻节点之间的距离为b/2。节点A，C，F，I均受到大小为P=35 kN、方向竖直向下的载荷，节点B，E，H均受到大小为Q=120 kN、方向竖直向上的载荷。

由于工作条件发生了变化，图1所示的悬臂式桁架原有的结构不再满足新的使用要求，需要对其进行改进与优化。由于空间有限，在改造该悬臂式桁架时，对其结构尺寸提出了一些新的要求，包括其总长4a不少于4 m但不超过8 m，其总高b不少于1 m但不超过3 m，每个杆件的横截面积A不少于700 mm2但不超过1 400 mm2，且K和L两处铰支座的约束力均不得超过300 kN，并取安全系数S为15。在满足上述要求的同时，还应满足在给定载荷的作用下，使节点A的挠度尽可能小。

2.2将目标函数具体化

要想确定具体的目标函数和限制条件，首先需要对图1所示的桁架结构进行静力学分析，以求出K和L两处的约束力以及各个杆件的轴力。取此桁架结构整体为研究对象，解除铰支座K和L处的约束，由于K是固定铰支座，解除该处的约束后可以用水平和竖直2个相互正交的约束力代替;L是可动铰支座，因而只有1个水平方向的约束力[13]。桁架所受的各个力形成了平面任意力系，因而可以列出3个独立的平衡方程，并由此解得铰支座K和L两处的约束力，其中，K处的水平约束力为FKX=（6Qa-10Pa）/b，竖直约束力为FKY=（3Q-4P）;L处的约束力为FL=（6Qa-10Pa）/b。

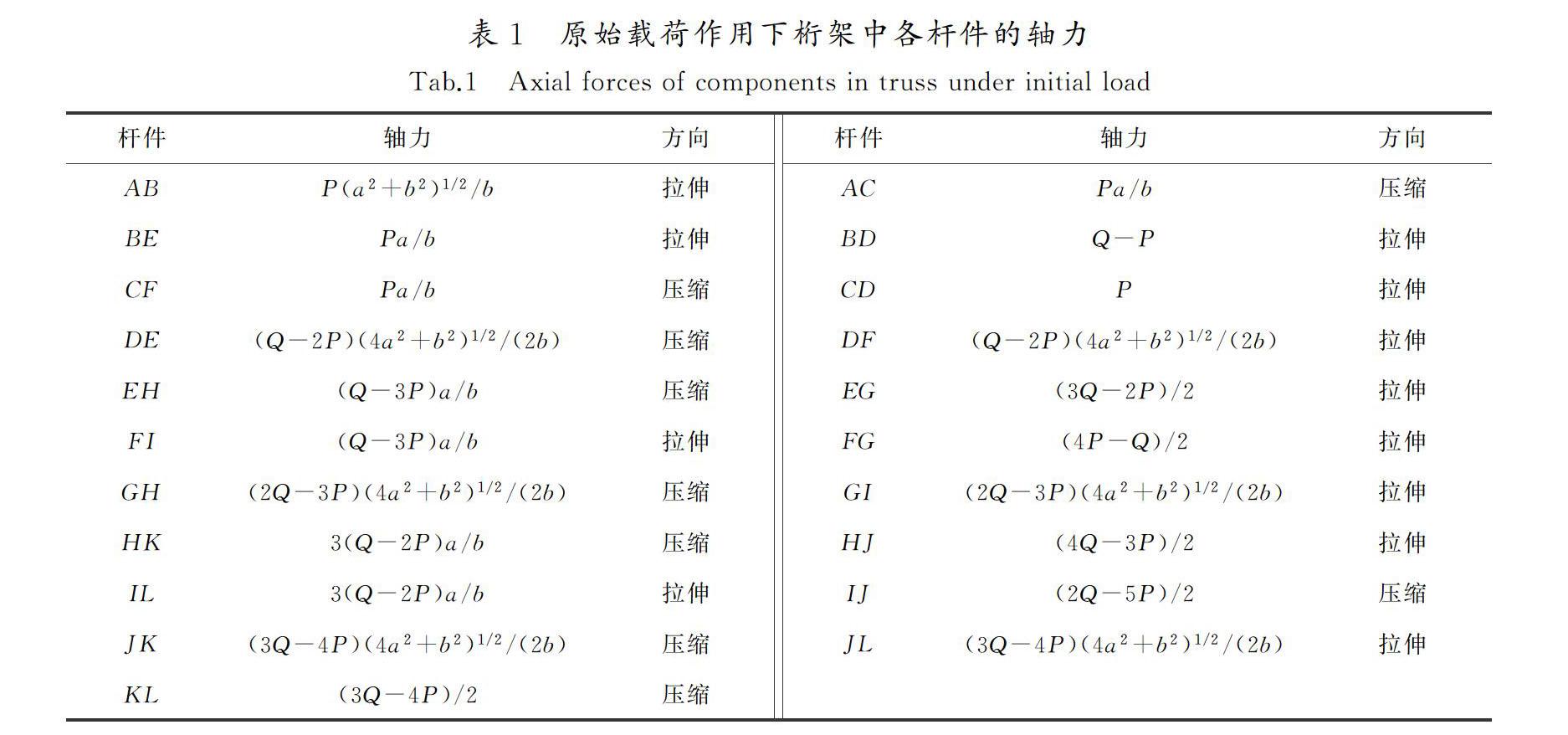
然后利用节点法，分别求出此桁架结构中各个杆件在原始载荷作用下的轴力，计算结果如表1所示。

由表1可知，在原始载荷的作用下，桁架结构中的各个杆件所受轴力的方向并不相同。由工程概况中给出的载荷大小，可以判断出此桁架结构中的各个节点都有向上运动的趋势，因而位于该结构上方的杆件一般都承受压缩载荷，结构下方的杆件一般都承受拉伸载荷，且越靠近铰支座的杆件，所受的轴力越大。

去掉该结构所受的所有载荷，并在节点A施加1个方向竖直向上，大小为1的单位载荷R，利用类似的方法，可以得到在此单位载荷R的作用下，此结构中各个杆件的轴力，计算结果如表2所示。

由表2可知，由于施加的单位载荷R的方向是竖直向上，因而该桁架结构总体的变形趋势与原始载荷作用下该桁架结构的变形趋势大致相同。除此之外，在单位载荷R的作用下，该桁架结构中各个杆件轴力的方向也与原始载荷作用下该桁架結构中各个杆件轴力的方向不完全相同。事实上，这是一种正常现象，在计算时只需要按照单位载荷法规定的符号要求代入莫尔积分的表达式即可。

由表3可知，当水平方向相邻2节点之间的距离a=1 m，铰支座K和L之间的距离b=2.6 m且杆件的横截面积A=1 400 mm2时，悬臂端节点A的挠度取得最小值为3.473 mm。由一般的工程经验可知，对于一个悬臂式结构，外伸的长度越短，其悬臂端的挠度越小。除此之外，对于等直杆一类的构件，横截面积越大，其抗拉（压）刚度越大，越有利于抵抗外力产生的变形。因而，可以初步判断表3所示的优化结果是合理的。

3优化模型的合理性验证

为了判断上述用于优化此悬臂式桁架的非线性规划模型的合理性，本文利用ABAQUS软件对该模型的优化结果进行验证。具体的验证思路：1）利用表3所示的已经优化好的该悬臂式桁架中各个杆件的尺寸（水平方向相邻2节点之间的距离a、铰支座K和L之间的距离b、杆件的横截面积A），在ABAQUS软件中建立此悬臂式桁架结构的有限元模型;2）给建立好的有限元模型施加工程概况中所给出的各个载荷;3）通过计算在给定载荷下ABAQUS软件利用有限元法[1415]得出的节点A的挠度与表3中所示的节点A的挠度之间的相对误差，同时观察ABAQUS软件根据有限元法计算出的铰支座K和L处的支反力以及各个杆件中的最大应力σmax是否满足2.3节中的各项约束条件，来判断此非线性规划模型是否合理。

3.1有限元模型的建立过程

3.1.1创建几何模型并划分网格

在“部件”模块的“创建部件”对话框中，设置模型空间为“二维平面”、类型为“可变形”、基本特征为“线”，即可开始绘制此悬臂式桁架结构的草图。根据表3中给出的杆件尺寸，可以确定图1所示的悬臂式桁架结构中各个节点在二维平面内的坐标，分别为A（4 000 mm， 0），

然后给图2所示的几何模型划分网格。由于桁架结构中的各个杆件在承受外载荷时都只受轴向的拉力或压力，因而在划分网格时，可以将每个杆件视为1个网格单元，而杆件内部不必再细化网格。ABAQUS软件中默认桁架结构的网格类型为T2D2，这是一种专门为二维二节点桁架划分网格的网格单元类型。由于图2中的结构共有21个杆件，因而共需要划分21个网格单元。

3.1.2定义材料和截面属性

首先给各个杆件赋予相应的材料。由于此悬臂式桁架结构中的各个杆件在承受外载荷时发生的变形都是弹性变形，且沿各个方向的力学行为相同，因而需要在“属性”模块中创建一种各向同性材料，即用于制造各个杆件的Q235钢，其杨氏模量为211 000 MPa，泊松比为0.3。给各个杆件创建相应的截面，主要的创建步骤如图3所示。

由图3 a）可知，在设置杆件的截面类型时，可以选择“梁”类别中的“桁架”类型，且在ABAQUS软件中，“桁架”类型的截面形状默认为圆形。由图3 b）可知，桁架中杆件的横截面积被设置为1 400 mm2，与表3中给出的横截面积相同。

3.1.3设置边界条件和载荷

首先需要在初始分析中为铰支座K和L施加边界条件。由于铰支座K是固定铰支座，需要限制其在X和Y方向上的位移;铰支座L是可动铰支座，只需要限制其在X方向的位移。随后，在节点A，B，C，E，F，H，I处按工程概况施加相应的载荷，即可完成载荷和边界条件的设置。所有定义完成的载荷和边界条件如图4所示。

由图4可知，铰支座K处出现了相互正交的2个小三角形，表示限制了X和Y方向上的位移;铰支座L处出现了1个水平方向的小三角形，说明对X方向的位移进行了限制。此外，节点A，C，F，I处出现了竖直向下的箭头，节点B，E，H处出现了竖直向上的箭头，表示相应的载荷已经加载到了对应的节点上。

3.2有限元计算

3.2.1计算结果

将此悬臂式桁架结构的有限元模型提交，ABAQUS软件根据有限元法计算出了此桁架结构中各个节点在Y方向的位移、铰支座K和L的支反力以及各个杆件所受的应力，如图5所示。

由图5 a）—c）左上角的图例可知，杆件在某处的颜色越深，代表在该处杆件的相关物理量的数值越大。从图5 a）中看出，桁架的整体结构发生了向上的位移，且悬臂端的几个节点发生的位移较大;从图5 b）中发现，铰支座K处的支反力大于铰支座L处的支反力;由图5 c）可知，靠近铰支座K和L的杆件应力要大于远离铰支座K和L的杆件应力，且杆件HJ所受的应力最大。

3.2.2结果对比

利用ABAQUS软件的查询功能，可以获得节点A在竖直方向的位移、铰支座K的支反力以及杆件HJ所受的应力。经查询，节点A在竖直方向的位移大小为3.478 mm，与表3所示的计算结果之间的相对误差为0.14%;与此同时，铰支座K的支反力大小为262 kN，在规定的小于300 kN的范围内;另外，杆件HJ所受的应力的大小为133.9 MPa，也小于其许用值157 MPa。由此可见，本文所提出的非线性规划模型的优化结果是合理的。

4结语

通过建立一个以悬臂端节点挠度最小为目标函数，以杆件的长度、横截面积等结构尺寸、铰支座所受的约束力和杆件的最大应力为限制条件的非线性规划模型，初步确定了某悬臂式桁架结构的优化方案，并利用ABAQUS软件，根据有限元法判断该优化方案是否合理。主要的结论如下。

1）当水平方向相邻2节点之间的距离为1 m，两铰支座之间的距离为2.6 m，且杆件的横截面积均为1 400 mm2时，此悬臂式桁架的悬臂端节点的挠度最小。

2）ABAQUS软件利用有限元法计算出的结果与Python的计算结果基本吻合，且符合限制条件，因此可以证明本文提出的优化模型与优化方案都是合理的。

3）本文提出的优化模型不仅对优化悬臂式桁架结构具有一定的参考价值，也为解决其他类型的桁架结构（如简支式、外伸式或空间桁架）的优化问题提供了新思路。

4）在实际工程中，悬臂式桁架结构可能还会受到其他条件的制约，因而本文提出的优化模型中的限制条件还需要在未来的研究中进一步补充，以获得更为合适的优化结果。

参考文献/References：

[1]耿雪宵，黄旭就. 基于ABAQUS软件的三维桁架有限元分析[J]. 煤矿机械，2012，33（4）：113115.

GENG Xuexiao， HUANG Xujiu. Finite element analysis of threedimensional truss based on ABAQUS software[J]. Coal Mine Machinery， 2012， 33（4）： 113115.

[2]张国伟，乔东需，丁梦婷，等. 基于ABAQUS的M型型钢桁架楼板有限元分析[J]. 钢结构，2019，34（11）：6064.

ZHANG Guowei， QIAO Dongxu， DING Mengting， et al. Finite element analysis of Msection steel truss floor based on ABAQUS[J]. Steel Construction， 2019， 34（11）： 6064.

[3]袁国平，蒋永扬，吴晓宇. 大跨度拱形拉索桁架结构封闭煤场关键施工技术[J]. 钢结构，2019，34（12）：108113.

YUAN Guoping， JIANG Yongyang， WU Xiaoyu. Key construction techniques of a closed coal storage with longspan arched cable truss structure[J]. Steel Construction， 2019， 34（12）： 108113.

[4]廖能解，馬平，李健洪，等. 上下料桁架机器人仿真研究[J]. 机床与液压，2019，47（21）：914.

LIAO Nengjie， MA Ping， LI Jianhong， et al. Simulation study on loading and unloading material truss robot[J]. Machine Tool & Hydraulics， 2019， 47（21）： 914.

[5]李元章，鲁国富，任三元，等. 基于积木式的飞艇桁架式复合材料龙骨结构验证方法[J]. 复合材料科学与工程，2020（1）：6771.

LI Yuanzhang， LU Guofu， REN Sanyuan， et al. Verification method for composite keel structure of airship truss based on building blocks[J]. Composites Science and Engineering， 2020 （1）： 6771.

[6]崔宏林，李辉. 小型双体船桁架式连接桥结构强度评估及优化[J]. 舰船科学技术，2019，41（12）：1619.

CUI Honglin， LI Hui. Strength assessment and optimization of trussed corss structure for a small catamaran[J]. Ship Science and Technology， 2019， 41（12）： 1619.

[7]乔心州，王兵，彭先龙. 桁架结构非概率可靠性形状优化设计[J]. 应用力学学报，2020，37（1）：176182.

QIAO Xinzhou， WANG Bing， PENG Xianlong. Nonprobabilistic reliabilitybased shape optimization design of truss structures[J]. Chinese Journal of Applied Mechanics， 2020， 37（1）： 176182.

[8]郝宝新，周志成，曲广吉，等. 桁架结构拓扑优化的半定规划建模与求解[J]. 哈尔滨工业大学学报，2019，51（10）：1121.

HAO Baoxin， ZHOU Zhicheng， QU Guangji， et al. Modeling and solving of truss topology optimization problems based on semidefinite programming[J]. Journal of Harbin Institute of Technology， 2019， 51（10）： 1121.

[9]李彦苍，王旭. 基于信息熵的改进海豚群算法及其桁架优化[J]. 重庆大学学报，2019，42（5）：7685.

LI Yancang， WANG Xu. Improved dolphin swarm algorithm based on information entropy and its truss optimization[J]. Journal of Chongqing University， 2019， 42（5）： 7685.

[10]李沛豪，李东. 基于改进粒子群算法的桁架结构优化设计[J]. 空间結构，2018，24（4）：1622.

LI Peihao， LI Dong. Optimal design of truss structure based on the improved particle swarm optimization algorithm[J]. Spatial Structures， 2018， 24（4）： 1622.

[11]王俊岭，钟敬康，杨明霞，等. 基于非线性规划的综合管廊断面尺寸设计优化[J]. 隧道建设，2019，39（12）：20302035.

WANG Junling， ZHONG Jingkang， YANG Mingxia， et al. Design optimization of standard crosssection size of utility tunnel based on nonlinear programming[J]. Tunnel Construction， 2019， 39（12）： 20302035.

[12]刘鸿文. 材料力学Ⅱ[M]. 6版. 北京：高等教育出版社，2017.

[13]哈尔滨工业大学理论力学教研室. 理论力学Ⅰ[M]. 8版. 北京：高等教育出版社，2016.

[14]刘庆刚，魏青，韩伟信，等. 基于有限元法的V 型缺口平板应力集中系数研究[J]. 河北工业科技，2019，36（4）：240245.

LIU Qinggang， WEI Qing， HAN Weixin， et al. Study of the stress concentration factors of a Vnotched plate by using finite element method[J]. Hebei Journal of Industrial Science and Technology， 2019， 36（4）： 240245.

[15]QI Zhenchao， LIU Yong， CHEN Wenliang. An approach to predict the mechanical properties of CFRP based on crossscale simulation[J]. Composite Structures， 2019， 210（15）： 339347.